1. Introduction
Unmanned aerial vehicles (UAVs) have a wide range of applications [
1] such as wildfire monitoring [
2], smart farming [
3], aerial surveillance [
4], environmental monitoring [
5], goods transportation [
6] and structural damage mapping [
7]. Particularly, surveillance systems [
8] require resilience and flexibility to address issues such as drone failures and adverse communications. They can be achieved using swarm intelligence [
9] as a way of modifying the collective behaviour of the swarm by using individual parameters. The members’ interactions usually follow local rules based on pheromones and probabilities [
10], upper confidence trees [
11] or finite games [
12], among others [
13]. These strategies can be based on competitions [
14] or collaborations [
15] between members, having each approach its own advantages and disadvantages [
16]. The associated high dimensional search space makes these problems good candidates to be solved using an intelligent bio-inspired technique, such as evolutionary algorithms [
17].
Game-based approaches are commonly present in UAV swarms as a strategy of cooperation between members. Games have been used for cooperative search and surveillance [
18], energy-efficient communications [
19], beyond-visual-range air combat missions [
20], Vehicular Ad hoc NETworks (VANET) communications under adverse network conditions [
21], etc. In Evolutionary Game Theory (EGT) [
22], group interactions are modelled with the assumption that the surviving strategy is the one which reports outcomes higher than other possible strategies.
In this research work, we propose a surveillance system based on a swarm of UAVs patrolling an area divided into concentric security rings. UAVs in inner rings move slower than those in outer rings but consume also less energy, which allows them to fly for a longer period of time. This surveillance scheme features a compromise between maximum flying time (most of UAVs in the innermost ring) and maximum area coverage (a smart strategy to fly by different rings according to each UAV’s battery state). Consequently, our contributions can be summarised as follows:
A new Surveillance System Enhanced by Games of Drones (SuSy-EnGaD), based on cooperative UAVs that explore the area of interest arranged in concentric rings.
Three different approaches to obtain the optimal strategy taking into account maximum flying time and area coverage.
Two bio-inspired evolutionary algorithms adapted to this problem based on the well-known NSGA-II and a genetic algorithm.
The remainder of this paper is organised as follows. In the next section, we review the state of the art related to our work. In
Section 3, the SuSy-EnGaD architecture is presented. Our optimisation algorithms are explained in
Section 4 and the case studies are described in
Section 5. The experimentation done using simulations is presented in
Section 6, as well as the discussion of results. After that,
Section 7 brings conclusions and future work.
2. Related Work
In this section, we review research works related to our proposal. First, we go through the multi-objective optimisation of UAV related problems. Second, energy optimisation proposals are analysed. Third, surveillance systems using UAVs are reviewed. And finally, cooperative and competitive strategies for UAV swarms are commented.
Many problems related to UAVs are often modelled and solved as multi-objective ones. In [
23], a multi-objective path planning framework is proposed to explore a suitable path for a UAV operating in a dynamic urban environment. The authors use safety index maps to capture static (offline search) and dynamic (online search) obstacles. This path planning problem is addressed taking into account two objectives: shorten the travel time and avoid obstacles. A multi-objective optimisation algorithm to allocate tasks and plan paths for a team of UAVs is presented in [
24]. A genetic algorithm is used to minimise the mission completion time and can be tuned to prioritise coverage or connectivity. Results obtained via simulations indicate that by transmitting lower rate notifications in the network, the mission time can be shortened. In [
25] a multi-objective path planning approach based on the Crowd Distance-based NSGA-II (CDNSGA-II) method is proposed to find an optimal collision-free path for UAVs, taking into account both distance and safety. Experimental results show that the proposed algorithm can obtain up to 80% pareto optimal solutions (see definitions 1 and 2 in
Section 3) when compared with NSGA-II under simulated urban environments.
Battery saving is an important concern when using UAVs. An offline path planning algorithm is proposed in [
26] to ensure that UAVs have permanent connectivity and can always reach the base station to recharge their batteries. Different approaches for heterogeneous UAVs and multi-base stations were analysed to obtain safe paths using simulations. In [
27], an energy-efficient algorithm to optimise fixed-wing UAVs trajectories is proposed. The authors derive a theoretical model of the propulsion energy consumption of fixed-wing UAVs to define the efficiency of communications. They conclude that an optimised simple circular trajectory maximises the energy efficiency and apply their findings to more general itineraries. In our study, quad-rotor UAVs move inside circular rings using unpredictable zigzag trajectories and can change the flying ring during their mission. As we are proposing a surveillance system, area coverage is taken into account in the optimisation process and our results are obtained using a simulator. In [
28], the authors present a novel framework for stochastic UAV-assisted surveillance which considers battery constraints. The system uses energy-efficient random walks for flying patterns and probabilistic inspections. A centralised algorithm based on iterative geometric programming approximation was used to solve the problem and the experimentation was conducted using simulations. We propose random walks for sampling the problem’s solution landscape to confirm that it is a multi-objective problem. Our UAVs’ trajectories always depend on surveillance rings, random bounce angles, and the possible collaborations between drones.
Surveillance systems using UAVs is one of the most discussed applications of these “eyes in the sky”. Coordination between UAVs using chaotic mobility combined with pheromone trails is proposed in [
29]. In this approach, vehicles explore the surveillance area using detection cells arranged into concentric square rings, stochastically avoiding high concentrations of pheromones. An Evolutionary Algorithm (EA) optimises pheromone amounts and assigns rings to maximise early intruder detection and protect the base in the centre of the analysed scenarios. The advantages of using surveillance rings are discussed in [
29], where that approach is also compared with other strategies. In our present study, we are using actual circular rings and UAVs dynamically change rings during the mission by collaborating each other using different strategies. Our proposed trajectories are not using pheromones and they were evaluated using a simulator that includes the full UAV dynamics. Finally, a multi-objective optimisation and game approach were implemented for our current study.
Path planning and coordination of multiple UAVs to provide convoy protection to ground vehicles is proposed in [
30]. Different scenarios with stationary and moving convoys were analysed using UAVs, modelled as Dubins vehicles flying at constant altitude. The authors proposed a coordination strategy and optimal paths, also calculating the minimal number of UAVs required. In [
31], an optimal navigation algorithm allowing UAVs to determine their movement locally with a minor use of a central station is presented. UAVs perform surveillance task for a group of moving targets while avoiding obstacles. Simulations results using case studies having up to 600 targets are presented to confirm the system’s performance. Heterogeneous multiswarm approaches comprise the use of patrolling UAVs and UGVs (Unmanned Ground Vehicles) to serve as mobile refuelling stations [
32]. Emerging UAV-UGV inter-swarm collaborations are analysed in [
15], and in [
33], UAVs, UGVs and UMVs (Unmanned Maritime Vehicles) are combined to improve detections and area coverage on the land and sea.
Finally, we analyse some research works using Evolutionary Game Theory (EGT) [
22] approaches to model problems as well as to discover evolving strategies for optimisation [
34]. In EGT, players are populations of individuals who follow mixed strategies when playing bimatrix games. In contrast to classical game theory, the surviving strategy after a group of interactions achieves higher benefits than the case of players making rational choices. In [
35], packet forwarding strategies are optimised in a mobile wireless ad hoc network (MANET). A Prisoner’s Dilemma (PD) model (see
Section 3.3) and an EA are proposed to enforce cooperation between nodes. In [
16], competition or cooperation are both analysed as possible strategies for drones mapping a disaster area. The problem is modelled as allocation tasks to robots in a swarm under limited communications and partial information, and is solved by a competitive algorithm and a cooperative one. The latter was reported to allocate more tasks in all the analysed scenarios. A modified binary log-linear learning (BLLL) algorithm is proposed in [
36] to solve the covering problem using multiple UAVs. The cooperative search problem is modelled as a potential game and a novel action selection strategy for UAVs is proposed. Experiments simulating different mission environments were designed to evaluate the effectiveness and feasibility of the proposed learning algorithm.
Our research work has parts in common with these articles, e.g., cooperation using EGT, results obtained via simulations and bio-inspired multi-objective optimisation of UAVs’ trajectories. However, we propose a surveillance area arranged in concentric circular rings, having each one its own flying constraints, plus three approaches using multi-objective and single-objective evolutionary algorithms to calculate the configurations of the UAVs. Some analysed articles involving UAVs focus on visiting predefined targets frequently. Our surveillance proposal in turn, uses unpredictable trajectories to explore the whole area, balancing coverage and battery consumption, which is something critical for every system using UAVs. To the best of our knowledge, no previous work has proposed the evaluation and use of these five evolving strategies for UAV cooperation in a surveillance system using concentric circular rings and trajectories that cannot be easily predicted by trespassers.
3. Surveillance System Enhanced by Games of Drones (SuSy-EnGaD)
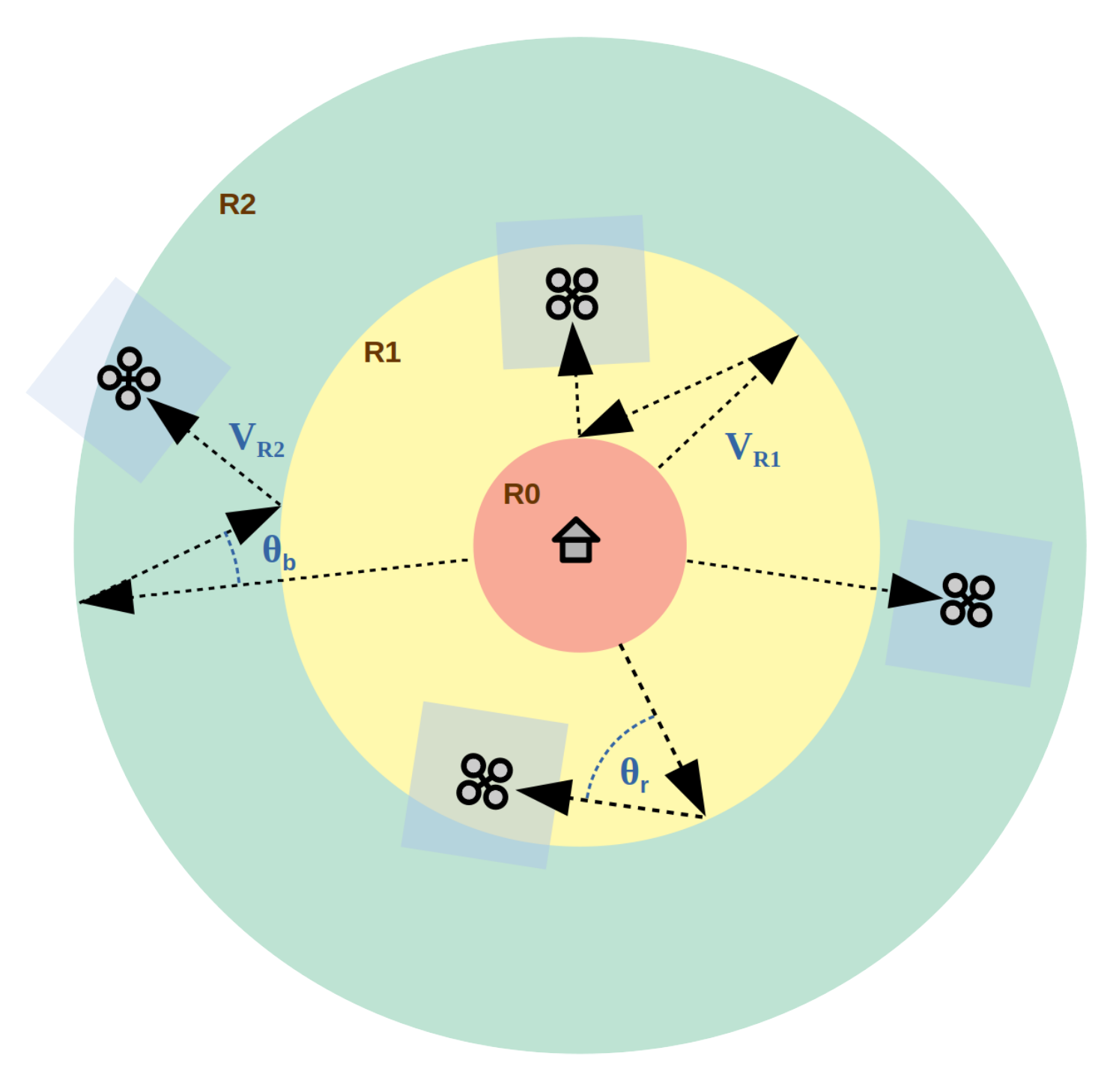
The proposed surveillance architecture is based on
M security rings where UAVs patrol the area of interest protecting a central base as illustrated in
Figure 1. The UAVs are equipped with a video camera directed downwards to scan the area and detect possible intruders. The altitude of the UAVs is fixed, so that the area scanned is about 10 × 10 m (assumed to be square instead of a 16:9 rectangle for simplicity). Since we are not analysing intruder detection rates in our study, we have calculated the area explored using the current position of each UAV, instead of using a specific camera model. This simplifies the simulation model increasing the overall efficiency without losing accuracy. The innermost ring,
, is a no-fly zone from where the UAVs depart and eventually return to recharge their batteries. Initially, all the UAVs are assigned to
and they can move to another ring
depending on their battery level and a series of autonomous decisions (strategy). Since each ring has its own speed restrictions (
), such as
, UAVs in inner rings consume less battery than the others in outer rings (and explore a smaller area). When a UAV reaches the external border it bounces back to the surveillance area with an angle
, randomly calculated such as
. On the contrary, when a UAV is on the border of a ring, the bouncing angle is
, randomly calculated in the range
. The use of a smaller range for
(compared with
) is to prevent UAVs to patrol the surface out of the surveillance area (secant trajectories) while the use of random values adds unpredictability to the UAVs’ trajectories, which is desired in surveillance missions.
The surveillance system as an optimisation problem presents two metrics to be maximised in our study: the area coverage and the vehicles’ flying time. By staying in inner rings, UAVs save battery and extend their flying time, but the area coverage is small. On the contrary, if there are too many UAVs in outer rings flying at higher speeds, their batteries will be drained too soon, reducing the system’s efficiency.
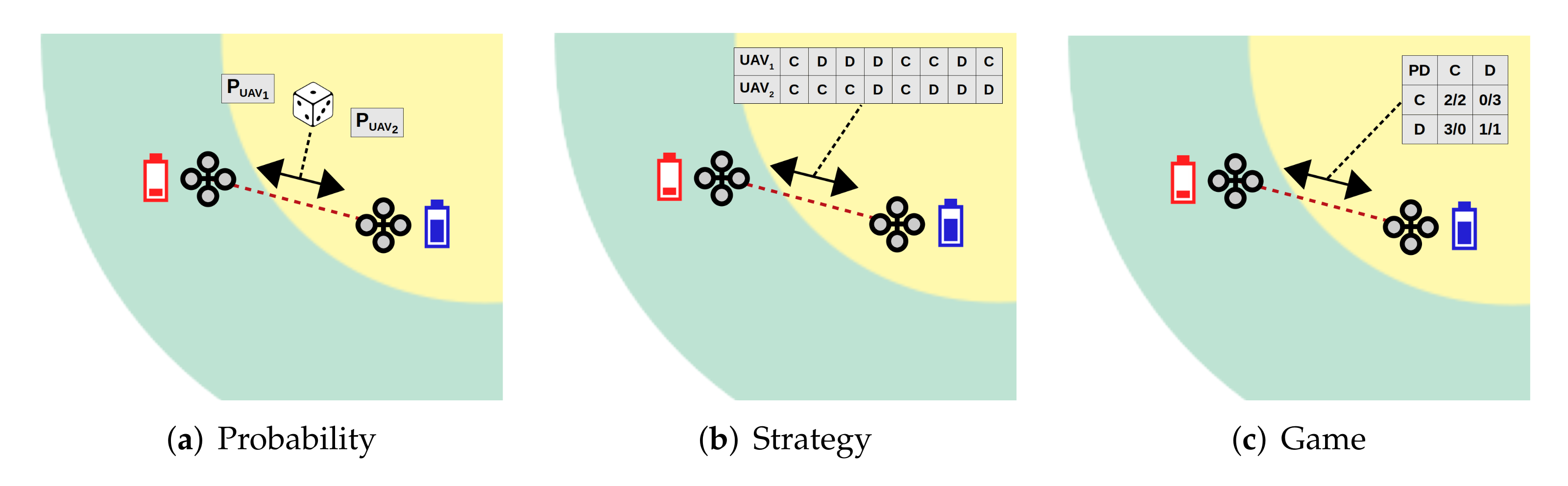
To dynamically control how UAVs spread by the surveillance area, we propose three approaches for UAVs to decide if they wish to cooperate with their partners by changing rings, or defects and stay in the current ones (
Figure 2). Indeed, we call cooperation when a UAV moves to a different flying ring after interacting with another UAV, and defection when it decides to ignore the proposal and stay in its current ring. There exist also a coordination between UAVs when they are in a collision trajectory which is mandatory to keep a safe distance between them (see
Section 5). Interactions occur when two UAVs are in their respective communication range (limited to 20 m in our study) where a new ring, in case of cooperation, is calculated according to the relative battery state and the UAV position in the map. Consequently, depending on the decision rules, if both UAVs are in the same ring, the UAV with lower battery charge will move to the next inner ring (if any) and the other will move to the next outer ring (if it cooperates). Otherwise, they will change rings independently of the battery state, which enforces the use of strategies to improve the global metrics of the system by making local decisions (mini-games) that sometimes might be adverse for one or both players (altruism). Despite that, if one UAV (or both) decides not to cooperate, it (they) will stay in the same ring, regardless their battery charge. For efficiency reasons, there is a minimum time between games, i.e., 20 s, and a minimum amount of battery is also required, i.e., 20%. When one UAV has begun a game with another, any other game proposal is also discarded during the next 20 s.
The first two approaches to optimising SuSy-EnGaD consist in modelling and solving a multi-objective optimisation problem (MOP). In the Probability and Strategy approaches, instead of a single solution, a set of pareto optimal solutions are obtained for the two metrics to be maximised: flying time and area coverage. Flying time corresponds to the time at which one of the UAVs in the swarm reaches 10% of battery (giving it enough time for a safe return to base for recharging). Area coverage was measured as the percentage of the area scanned by the onboard cameras (an area of 10 × 10 m).
The main goal of solving a MOP is to find a set of feasible solutions that maximises (in our case, although it can be also defined in terms of minimisation) the objective function vector , where D is the number of objectives (two in our study), according to the notion of Pareto-optimality, defined as follows:
Definition 1. Given the vectors and , we define the solution dominance in a maximisation problem as Definition 2. The set of solutions not dominated by any other in the solution space S is called the Pareto optimal set (P), defined as The third approach, Game, consists in maximising the average score (outcome) achieved by the UAV swarm as a method for obtaining a solution to the surveillance problem. In this case, it is clearly a single-objective optimisation problem. In the following sections, we describe each approach in detail.
3.1. Probability Approach
In the
Probability approach each UAV
i has a real parameter (
) in the range
defining its cooperation probability. The problem representation is the vector
composed of
N probability values (Equation (
3)), where
N is the number of UAVs. Different cooperation probability values modify the way UAVs interact, allowing strategies that save battery as well as others that cover a bigger area.
3.2. Strategy Approach
The
Strategy approach proposes for each UAV a strategy defined as a list of bits where “1” means cooperation and “0”, defection. The problem representation is the vector
containing the list of
B strategy bits (
) for each one of the
N UAVs (Equation (
4)). In our study, we have set
as a balance between problem complexity (similar to the
Probability approach) and strategy accuracy. This is a cyclic approach, different from
Probability, where after six games the strategy of one UAV starts over.
3.3. Game Approach
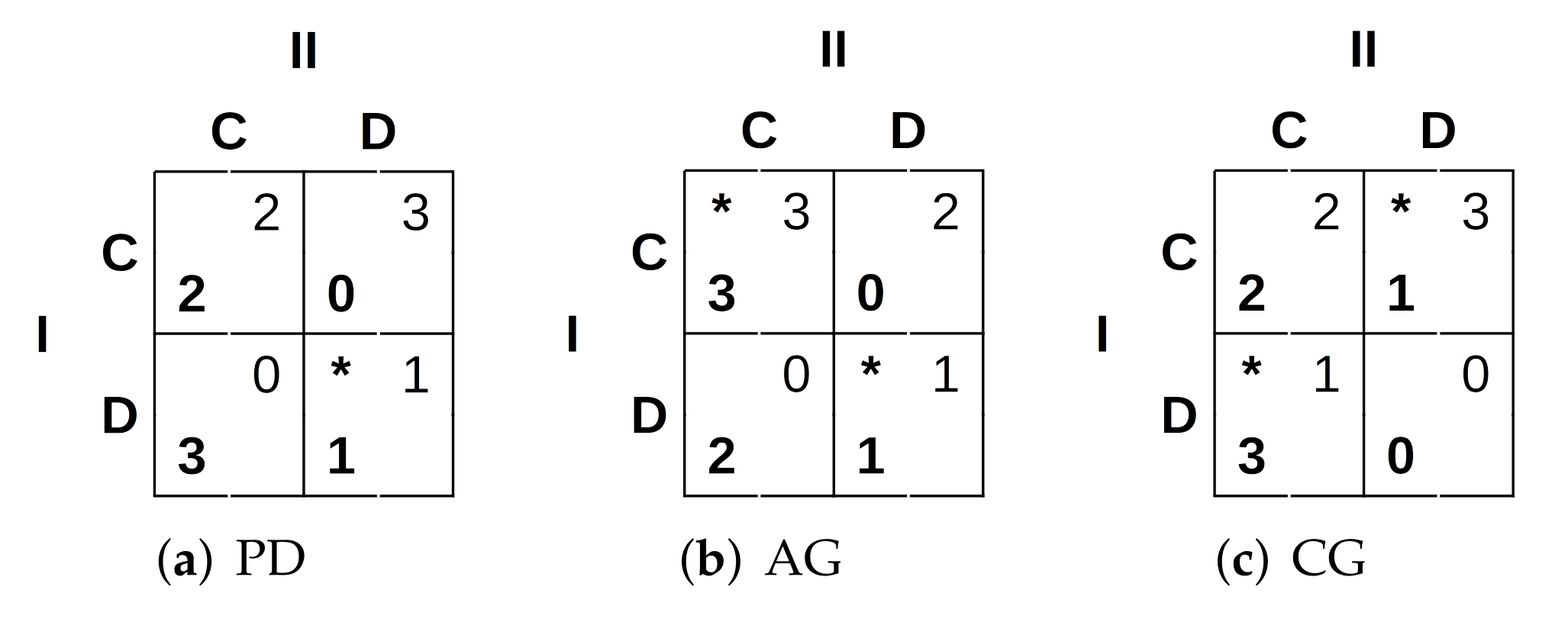
We propose a third approach based on two-person games. In this case, when two UAVs have to decide a possible cooperation, they will do so by trying to maximise their outcome according to the reward matrices shown in
Figure 3, where the Nash equilibria [
37] are marked with asterisks.
In the prisoners’ dilemma (PD) [
38], two prisoners are given the choice of testifying against each other or keeping silent. The best possible outcome is defecting when the other player cooperates (DC). Then comes mutual cooperation (CC) and finally mutual defection (DD) as represented in
Figure 3a. The assurance game (AG) (
Figure 3b) represents the situation in which a person would be willing to cooperate as long as he/she is assured that their partner would cooperate as well. The better outcome is obtained when there is mutual cooperation (CC), although mutual defection (DD) is also one of the game’s equilibria as one person will defect if it thinks that the other will also defect [
38]. And finally, the game of chicken (CG), also known as the game of dare, in which two cars are driven one towards the other. The driver who turns away is “chicken” and loses while the other wins. Of course, if no one turns, both drivers die and lose (DD) [
38]. There are also two equilibria in CG, unilateral cooperation (CD) and unilateral defection (DC) as shown in
Figure 3c.
In the
Game approach, the UAVs are engaged in a finite two-person game with limited interaction [
39]. As the number of iterations is given by how frequently the UAVs meet each other during the simulation, we propose to calculate the best strategy for each player using a bio-inspired meta-heuristic: a genetic algorithm. The
Game approach uses the same problem representation as in the
Probability approach (Equation (
3)), although, in this case, the objective is maximising the average score of UAVs by modifying their cooperation probability. The evaluation function for this single-objective problem is shown in Equation (
5). There,
outcome refers to the average score achieved by a given UAV after a number of iterations (games) with the other UAVs, obtained from the simulation.
4. Optimisation Algorithms
Multi-objective optimisation problems are usually solved by using one of the following techniques: (i) converting the multi-objective problem into a single-objective one by using a weighted-sum function and (ii) getting a set of Pareto optimal solutions and selecting the most appropriated according to an expert’s criterium. The former, despite its simplicity, implies a difficult weight selection that restricts the working solutions during the optimisation process. On the other hand, the latter involves the use of a more complex algorithm, although it increases the versatility and does not require the normalisation of the objectives into the same order of magnitude.
We propose two evolutionary bio-inspired techniques to optimise the parameters of our three approaches. These are efficient methods for solving combinatorial optimisation problems which simulate processes present in evolution such as natural selection, gene recombination after reproduction, gene mutation, and the dominance of the fittest individuals over the weaker ones. Our proposed optimisation algorithms are the Non-dominated Sorting Genetic Algorithm (NSGA-II) for the Probability and Strategy approaches (multi-objective) and a generational Genetic Algorithm (GA) for the Game approach (single-objective).
These optimisation algorithms are to be run in a computer cluster to obtain the optimal solutions for each case study in an initial configuration stage (offline). The solutions achieved, consisting of the optimal configuration of the UAV swarm for each case study, are to be used as the parameters for each UAV to rule the possible collaborations during the surveillance missions (online).
4.1. Non-Dominated Sorting Genetic Algorithm (NSGA-II)
NSGA-II [
40] is a multi-objective optimisation algorithm that implements a non-dominated sorting approach to rank solutions based on their Pareto dominance relation. Following the pseudocode in Algorithm 1, after initialising the population composed by
individuals, the main loop is executed while the termination condition holds (3000 evaluations in our case). The operators used were chosen according to our problem characteristic and representation. The selection operator is Binary Tournament, Single Point Crossover (
), Integer Polynomial Mutation for the
Probability approach and Bit Flip Mutation for the
Strategy approach (for both
, where
L is the length of the configuration vector), and finally, the replacement operator uses the Ranking and Crowding distance selection for maintaining solution diversity [
40].
| Algorithm 1. Pseudocode of NSGA-II. |
procedureNSGA-II () ▹ Q=auxiliary population ▹ P=population while not do end while end procedure
|
4.2. Genetic Algorithm (GA)
The proposed GA [
41,
42] is a single-objective optimisation algorithm featuring a population of individuals which evolve to maximise (in our case) their fitness value. The pseudocode of GA is presented in Algorithm 2. Initially, 28 individuals (
) for the population
P are generated and while the termination condition holds the main loop is executed. This is a generational GA where the working population
Q has the same number of individuals as
P (
). We used Binary Tournament as selection operator, Single Point Crossover as recombination operator, Integer Polynomial Mutation as mutation operator, and an elitist replacement. The parameters of GA are the same as in NSGA-II, i.e., 3000 evaluations,
and
.
| Algorithm 2. Pseudocode of GA. |
procedureGA() ▹ Q=auxiliary population ▹ P=population while not do end while end procedure
|
4.3. Genetic Operators
In this section, we describe the operators used in both algorithms. We have used the implementation provided by the jMetalPy package [
43] for the operators and both optimisation algorithms.
4.3.1. Selection
We have used Binary Tournament [
44] as selection operator. It is described in Algorithm 3 where two random samples are taken from the population
Q. If it is the multi-objective case (NSGA-II), each sample comprises a pareto from the population while in the case of single-objective optimisation (GA), each sample is an individual representing one configuration of the surveillance system. Then, the samples are compared in terms of dominance (pareto fronts) or fitness (system configurations) and the best of them is included in
, which will become the working population for the current generation. This process is repeated until the
required individuals are obtained.
4.3.2. Crossover
Single Point Crossover [
45] was used as crossover operator in both algorithms. As shown in Algorithm 4, two individuals
and
are taken from the population
Q to be recombined subject to the crossover probability
. After selecting the crossing point
p, the components of
and
are swapped from the position
p to the end of each solution vector. The new resulting vectors
and
are now added to the new working population
. By doing so, the optimisation algorithm explores different areas of the solution space in parallel, searching for new promising configurations for the swarm.
| Algorithm 3. Pseudocode of the Binary Tournament Selection Operator. |
functionSelection(Q) for do ▹ will have individuals ▹ randomly takes two individuals from Q ▹ they are pareto fronts in NSGA-II if then ▹ compare in terms of fitness/dominance else end if end for return end function
|
| Algorithm 4. Pseudocode of the Single Point Crossover Operator. |
functionCrossover() for all do ▹ all the individuals in Q, taken in pairs if then ▹ crossover probability ▹ crossing point p, L is the length of the solution vector for do ▹ swaps vector’s components from p to L end for end if ▹ adds the new vectors to the result end for return end function
|
4.3.3. Mutation
Two mutation operators were used. Bit Flip Mutation for the binary representation (
Strategy approach) and Integer Polynomial Mutation for the
Probability and
Game approaches. They are meant to make small variations to the configuration vectors and explore the neighbourhood of the good solutions already found. The selected value for
stochastically selects one position of each solution vector (individual of the working population) to be changed. The Bit Flip Mutation [
46] consists in randomly selecting bits in the solution vector to be flipped as shown in Algorithm 5. After all the individuals were considered for a possible mutation the resulting population
is returned.
The Integer Polynomial Mutation [
47] was selected to work with the numeric values in the vector of probabilities. To simplify the search process we have worked with integer values between 0 and 100 to represent probabilities between 0.0 and 1.0 with an accuracy of two decimal places. The Algorithm 6 shows the pseudocode of this operator. It can be seen that for each position in the solution vector subject to be mutated, four values are calculated depending on the current position’s value, the maximum allowed value (100), and a new random value (
) as well. A
value is calculated depending on
, to modify the original value, subject to the right range of values.
| Algorithm 5. Pseudocode of the Bit Flip Mutation Operator. |
functionBitFlipMutation() for all do ▹ all the individuals in Q for do ▹i goes from 1 to L (the length of the solution vector) if then ▹ mutation probability ▹ bit flip end if end for end for return end function
|
| Algorithm 6. Pseudocode of the Integer Polynomial Mutation Operator. |
functionIntegerPolynomialMutation() for all do ▹ all the individuals in Q for do ▹i goes from 1 to L (the length of the solution vector) if then ▹ mutation probability ▹ by default if then ▹ equiprobable else end if ▹ keeps it in range [0, 100] ▹ nearest integer value end if end for end for return end function
|
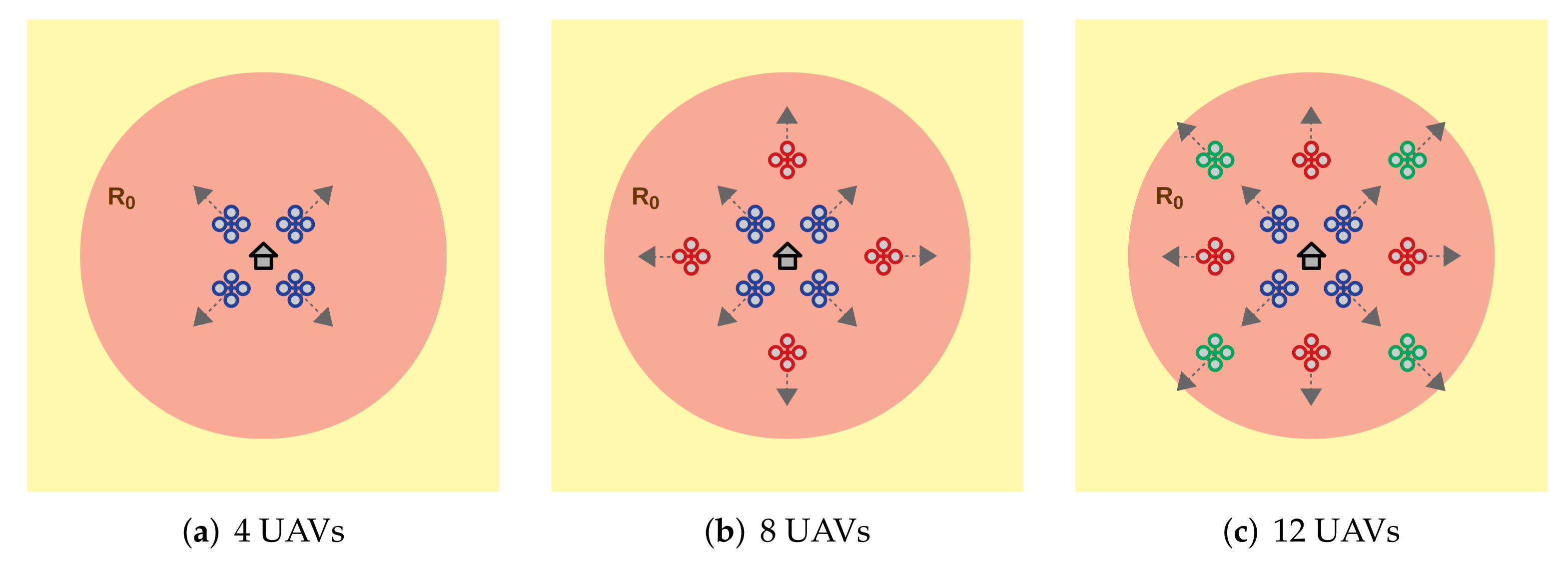
5. Case Studies
To evaluate SuSy-EnGaD using the three approaches previously discussed, four case studies are proposed featuring different numbers of UAVs and map dimensions. The characteristics of the case studies are detailed in
Table 1, as well as the nomenclature used, i.e., UAVS.MAPSIZE. The innermost ring corresponds to the area from where the UAVs depart, and after this initial stage, it becomes a no-fly zone. The evaluation of the UAVs configuration, according to each approach, was performed using the ARGoS simulator [
48]. ARGoS is a multi-physics robot simulator that can simulate large-scale swarms of robots of any kind, efficiently. In our study, we simulate UAVs using the eye-bot drones [
49] provided by ARGoS, including their communication and battery consumption models. This allows us to efficiently test multiple configurations keeping in mind reliability and safety since a wrong configuration does not end in a catastrophic collision while many scenarios can be evaluated in parallel. Depending on the number of robots, the departing point and the initial heading angle was predefined to avoid excessive use of the collision avoidance algorithm at the beginning of the simulation.
Figure 4 shows the initial configuration for 4, 8, and 12 UAVs, all departing from the innermost ring (in red).
The designed collision avoidance algorithm relies on repelling forces between UAVs as described in Algorithm 7. Given
, the distances between
u and the rest of vehicles in
are calculated. Those UAVs closer than a minimum distance
(a fixed parameter, e.g., 9 m) modify the vector
, which will contain the resultant repelling force. As a result of this coordination,
is to be used to modify the original trajectory of
.
| Algorithm 7. Collision Avoidance Algorithm. |
functionCollisionAvoidance() for all do ▹ all the UAVs if then if then ▹ end if end if end for return end function
|
6. Simulation Results
First, we analyse the proposed metrics, flying time and area coverage, to confirm that the use of a multi-objective optimisation is appropriated. Second, we have optimised the four case studies using NSGA-II for the Probability and Strategy approaches. Third, we have used the proposed GA to maximise the average score obtained by the UAVs in the four case studies using the Game approach (three two-person games). Finally, an analysis of the UAVs’ trajectories is given.
We have used the jMetalPy package [
43] to implement both optimisation algorithms. Our experiments were performed doing parallel runs in the HPC facilities of the University of Luxembourg [
50]. Since the use of the ARGoS simulator implies long evaluation times to preserve the realism (10 simulation ticks per second), we have evaluated each algorithm’ generation (28 individuals) in parallel on computing nodes equipped with Intel Xeon Gold 6132 2.6 GHz and 128 GB of RAM. The total optimisation time (600 runs in total) was equivalent to 1750.8 h (about 73 days).
6.1. Metric Analysis
In this experiment, we analyse the existence of correlations between the metrics used in our study. We have performed 30 random walks of 20 steps each, for 4, 8 and 12 UAVs, (we have considered that 1800 steps in total are enough for getting a significant sample of the problem’s solutions) and calculated the Pearson correlation coefficients [
51] shown in
Table 2. Note that the random walks are performed on the system configuration, i.e., a vector of probabilities as defined in Equation (
3), to sample the solution landscape of the problem. The UAVs are always following the SuSy-EnGaD trajectories based on surveillance rings.
It can be seen that 4 UAVs present some negative correlation between flying time and area coverage, so that one increases when the other decreases and vice versa. On the contrary, the metrics of 8 and 12 UAVs are not correlated (Pearson coefficient approximately equal to 0). Consequently, we can confirm that the use of a multi-objective optimisation algorithm (NSGA-II) is appropriate to obtain not one but many non-dominated solutions to our surveillance problem. After that, an expert can decide which solution suits better its needs and whether higher coverage levels could be prioritised against flying times or the other way round.
6.2. Multi-Objective Optimisation
The next experiment consisted of the optimisation of the four case studies using a multi-objective algorithm (NSGA-II). We have performed 30 runs for the
Probability and
Strategy approaches on each case study (240 runs of NSGA-II in total) to get the results shown in
Figure 5. We have plotted the empirical attainment functions (EAF) [
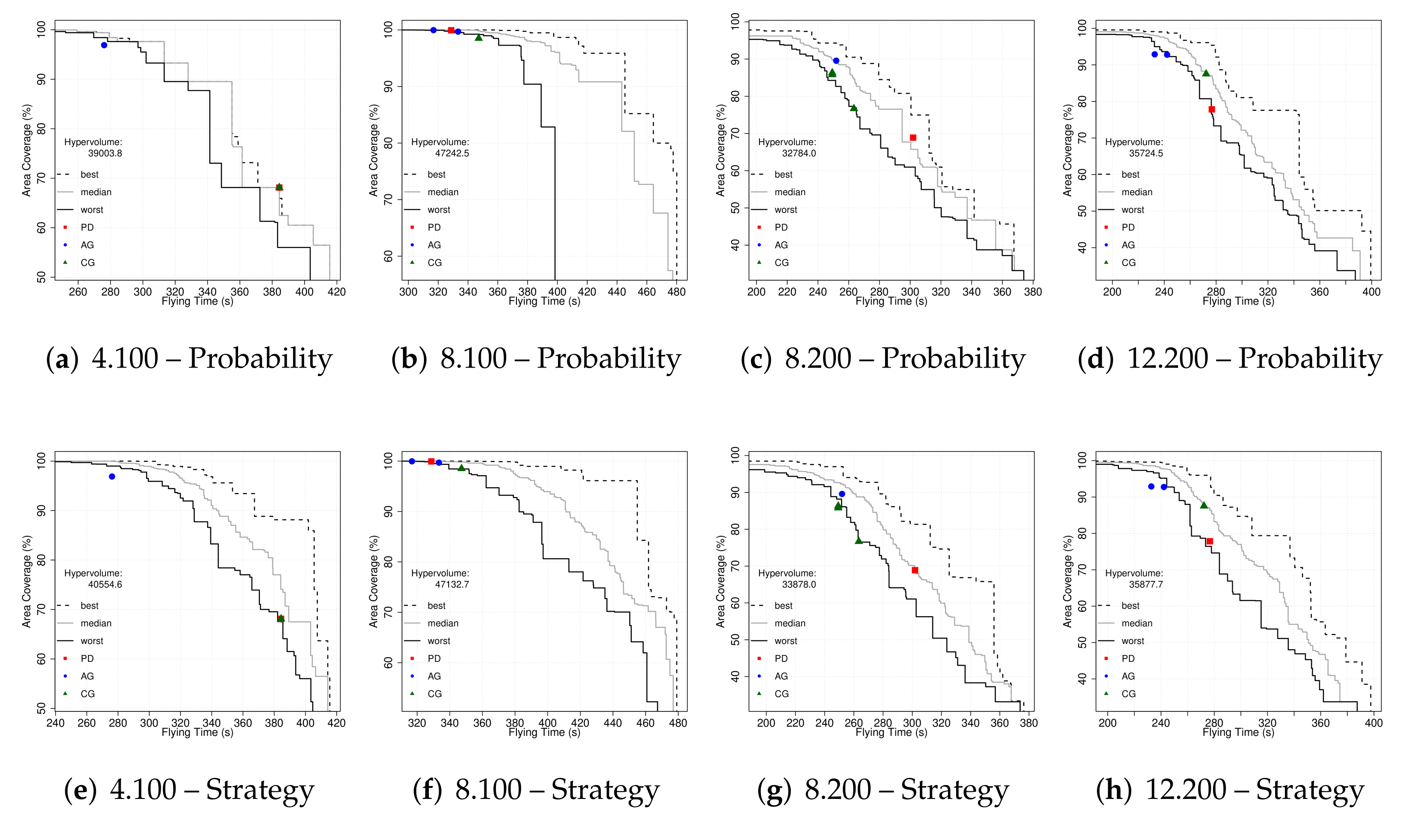
52] describing the probabilistic distribution of the outcomes obtained by NSGA-II. Additionally, the hypervolume of the union of all sets using the reference point 0,0 is reported to compare the results of both approaches on each case study.
We can see that both strategies obtained similar results and that differences between hypervolumes are always under 4%. One optimisation run for 8.100 using the
Probability approach seems to have suffered from stagnation, which can be clearly seen through the worst-case depicted in
Figure 5b. That is one of the reasons why we performed 30 runs of stochastic algorithms. Now, one result from the set of results in each Pareto front could be selected and the associated configuration (whether it is composed by a set of probabilities or a list of bits) is to be used to set up the surveillance system prioritising coverage, flying times or a compromise solution. A different approach based on games is used in the next set of experiments described in the following section.
6.3. Game Results
A different optimisation approach consists in using games to model each UAV interaction. As the objective is the maximisation of the average score of the swarm, we have used a single-objective GA.
Table 3 shows the result of this optimisation process where 360 runs of GA were performed (30 per game and case study) to perform a reliable statistical analysis since we are working with a stochastic optimisation algorithm. It can be seen that UAVs playing the assurance game (AG) have maximised the average score of the swarm (fitness value). The game of chicken (CG) achieved the best maximum and minimum results for 4.100 although the median is still the same as in AG. All the results are statistically significant as shown by the reported Friedman ranks and Wilcoxon
p-values.
We have plotted the corresponding metric points (flying time vs. area coverage) over the Pareto fronts graphics in
Figure 5. It is interesting to see that AG favours high area coverage values in all case studies, while PD’s results are obtaining better flying times in three of the case studies. UAVs playing CG are usually in a middle point between the other two games. Some games present different metric values for the same maximum scores (different trajectories, same game results) as depicted in
Figure 5.
As a piece of complementary information about the optimisation process performed by the GA, we show in
Figure 6 the boxplots with the distribution of the results achieved for each game and case study. We can see that the scores for AG are higher in most of the cases, except by 4.100 where CG presents some outliers revealing a higher average score (fitness) for the swarm. Looking at the scores in
Figure 3, we see that the highest values obtained from cooperation (CC) are provided by AG. Consequently, we can assume that this was the strategy followed in the majority of cases by the UAVs.
The extreme solutions for all the approaches are shown in
Table 4. Note that we have used the default consumption model provided by ARGoS for all our experiments. Hence, maximum flying times ought to be longer than 480 s if other models of drones are used. In the next section, an analysis of the UAVs’ trajectories is presented to better understand their behaviour under different configurations.
6.4. Analysis of Games’ Trajectories
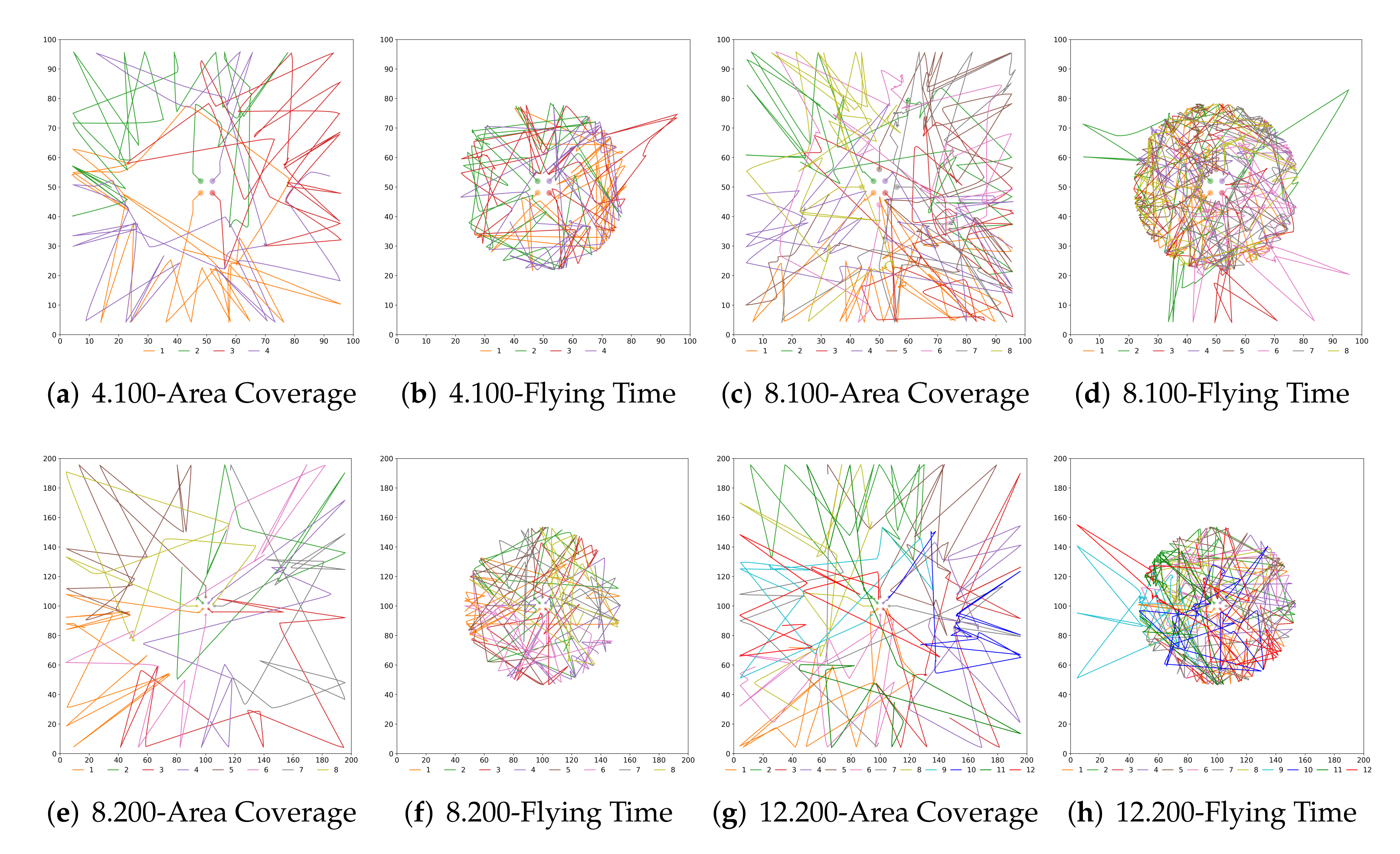
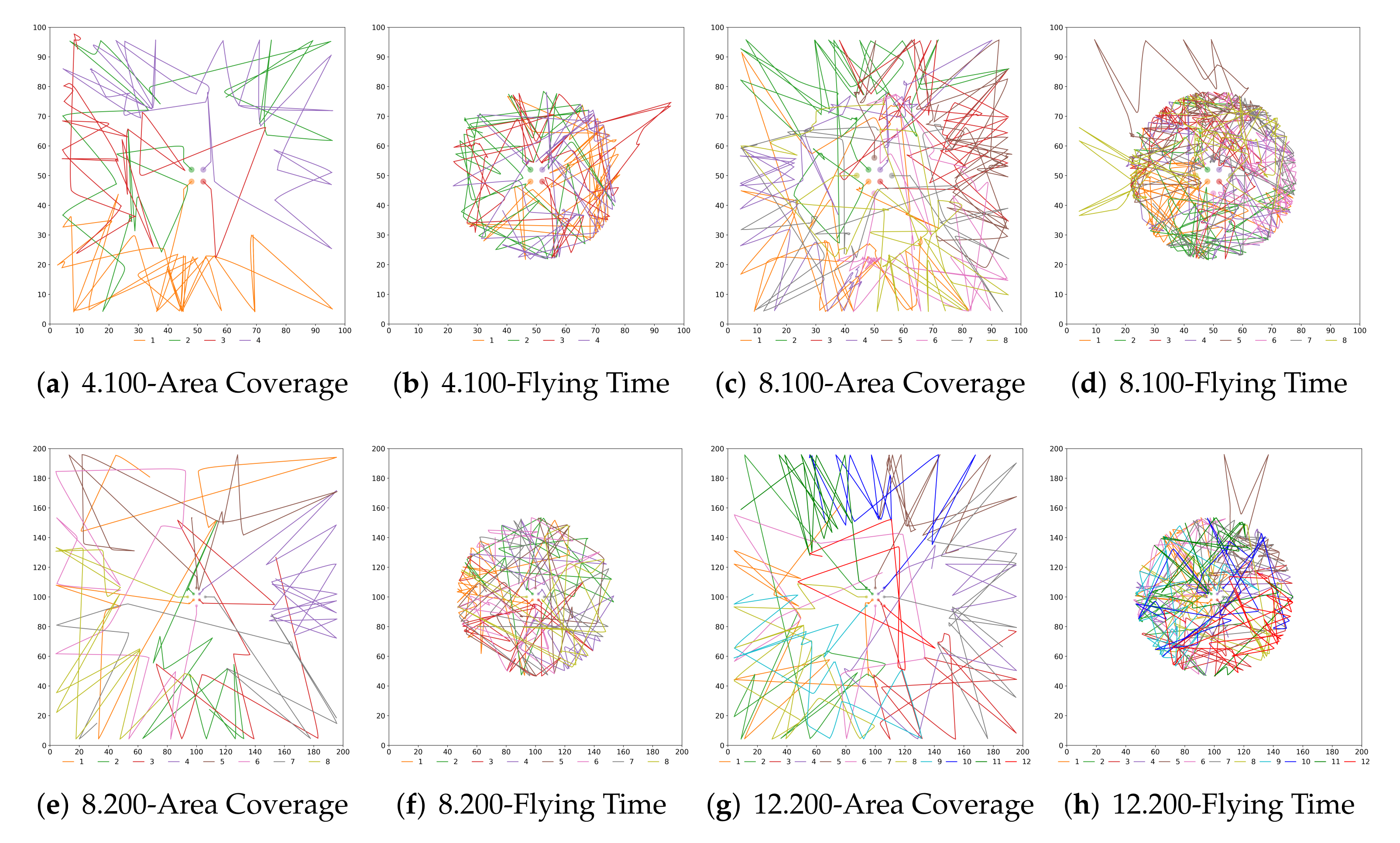
The objective of this last study is to better understand the implications of each configuration and approach and how a cooperation/defection decision modifies the swarm behaviour. We have already presented the numerical results but now in
Figure 7 and
Figure 8 the UAVs trajectories for the extreme solutions are depicted.
We can see that there exist many similarities in the trajectories when using
Probability and
Strategy. In the configurations maximising area coverage, the UAVs depart from the innermost ring and visit the other two rings regularly, where the surveillance mission takes place. On the contrary, when the objective of the swarm is maximising the flying time, most of the UAVs stay in the middle ring after departing from the centre. It is interesting to remark that the maximum flying time was sometimes achieved when some UAVs have a short excursion to the outer ring. That was unexpected as we believed that flying at a lower speed all the time would have been better for saving energy. As we can see, the less congested cases (
Figure 7f and
Figure 8f) are indeed according to our preliminary assumptions, since the rings’ areas are bigger. We believe that multiple iterations in a limited space, plus the effects of the collision avoidance algorithm, have made NSGA-II to find better solutions (in terms of battery consumption) by temporarily sending some UAVs to the outer ring.
7. Conclusions
In this research work, we have presented a new Surveillance System Enhanced by Games of Drones (SuSy-EnGaD), based on cooperative UAVs that explore the surveillance area modelled as concentric rings. We have proposed three different approaches to obtain optimal strategies focusing on maximum flying time and area coverage. The first two approaches, Probability and Strategy are addressed as multi-objective optimisation problems using the well-known NSGA-II. The third approach is related to the evolutionary game theory where prisoner’s dilemma, assurance game and game of chicken are proposed to rule possible cooperation between UAVs. This approach was optimised using a genetic algorithm maximising the average score of the swarm and the results were compared with the multi-objective approaches. We have tested SuSy-EnGaD on four different case studies featuring two map sizes and swarms of four, eight and twelve UAVs. Finally, the UAVs trajectories were analysed to better understand the best configurations in terms of flying time and area coverage.
Our results show that flying times up to 480 s can be achieved with a low area coverage, while on the other hand, a full area coverage is possible when the flying time is roughly under 250 s (depending on the case study). Vehicles’ trajectories have indicated a high concentration of UAVs in the inner surveillance ring to save battery (they fly at a reduced speed there), and a more balanced distribution of UAVs throughout the surveillance area to achieve high coverage rates. The single-objective Game approach obtained optimal solutions by maximising the swarm’s average score. Although the extreme values were obtained by using the multi-objective approaches, the Game approach turned out to be a different strategy to obtain particular solutions depending on the game selected.
In our simulations performed using a multi-physics robot simulator (ARGoS), we have observed UAVs’ trajectories visiting the entire surveillance scenario when area coverage was prioritised. On the contrary, almost all UAVs stayed in the inner ring when the objective was to keep a maximum flying time. Under this condition, we have observed some UAVs momentarily leaving the inner ring, which we believe is due to the collision avoidance algorithm as several UAVs were flying in a reduced area. These trajectories confirm the expected UAV behaviour and are in accordance with the numeric results obtained.
As a matter of future work we plan to test our proposal using a different number of security rings and UAVs. Previously, we have experimented with square rings and pheromones, in this current article we have improved the surveillance scenario using actual circular rings, and we wish to take advantage of this new architecture in future research works. We would like to try other different games to study the various solutions that can be achieved and also defining our own payoff matrices to obtain different single solution points from the pareto front. Despite the accuracy provided by ARGoS, we are working on increasing the realism of our approach testing the trajectories using actual drones where weather conditions, vision algorithms, and communication restrictions are to be considered. Another interesting future work would consist in using a communication layer featuring different packet loss rates to analyse how it would affect the swarm behaviour, especially the collision avoidance algorithm.