Drone Swarms in Fire Suppression Activities: A Conceptual Framework
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of the Drone Swarm System
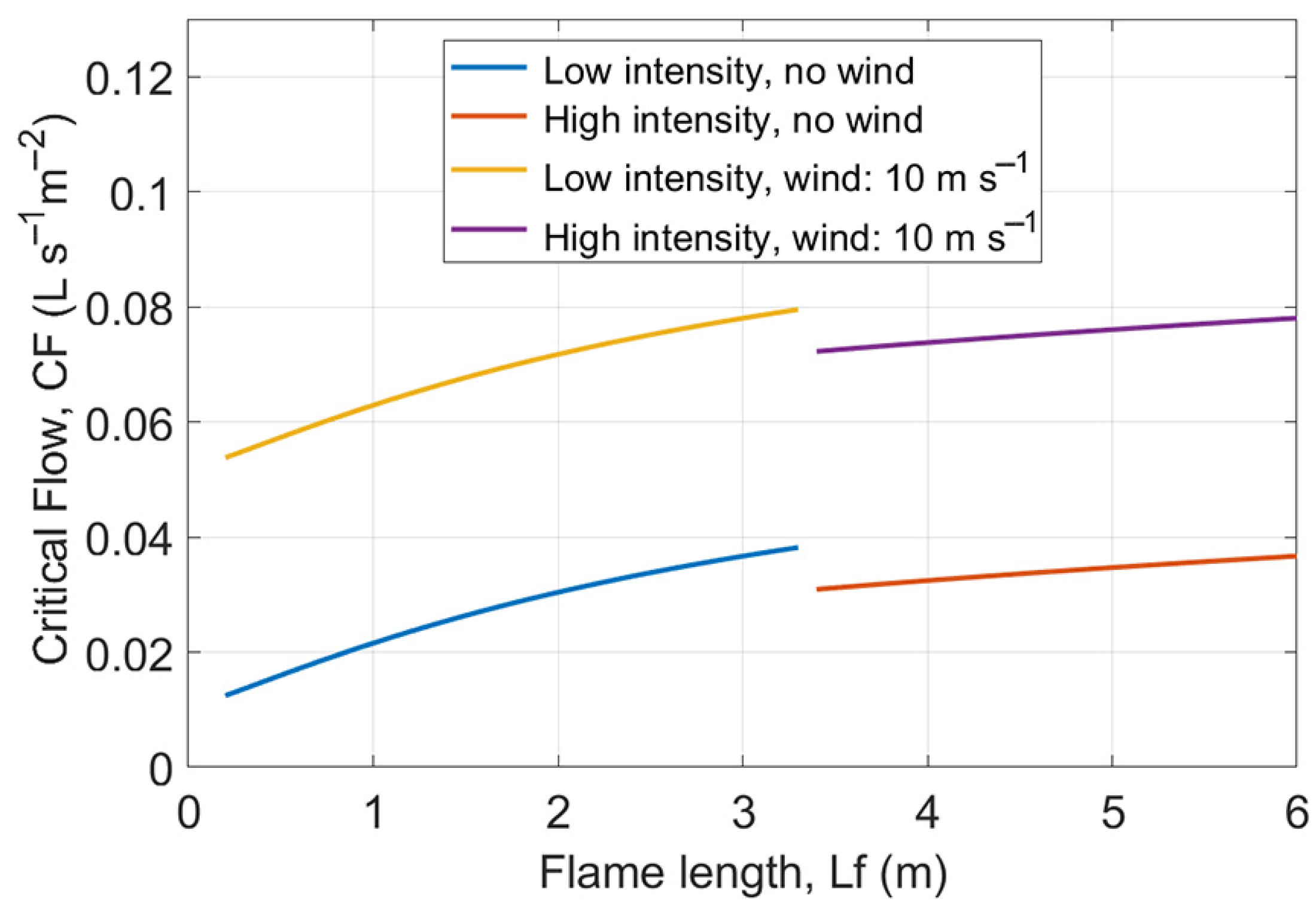
2.2. Calculation of Critical Water Flow Rate CF as Function of Flame Length
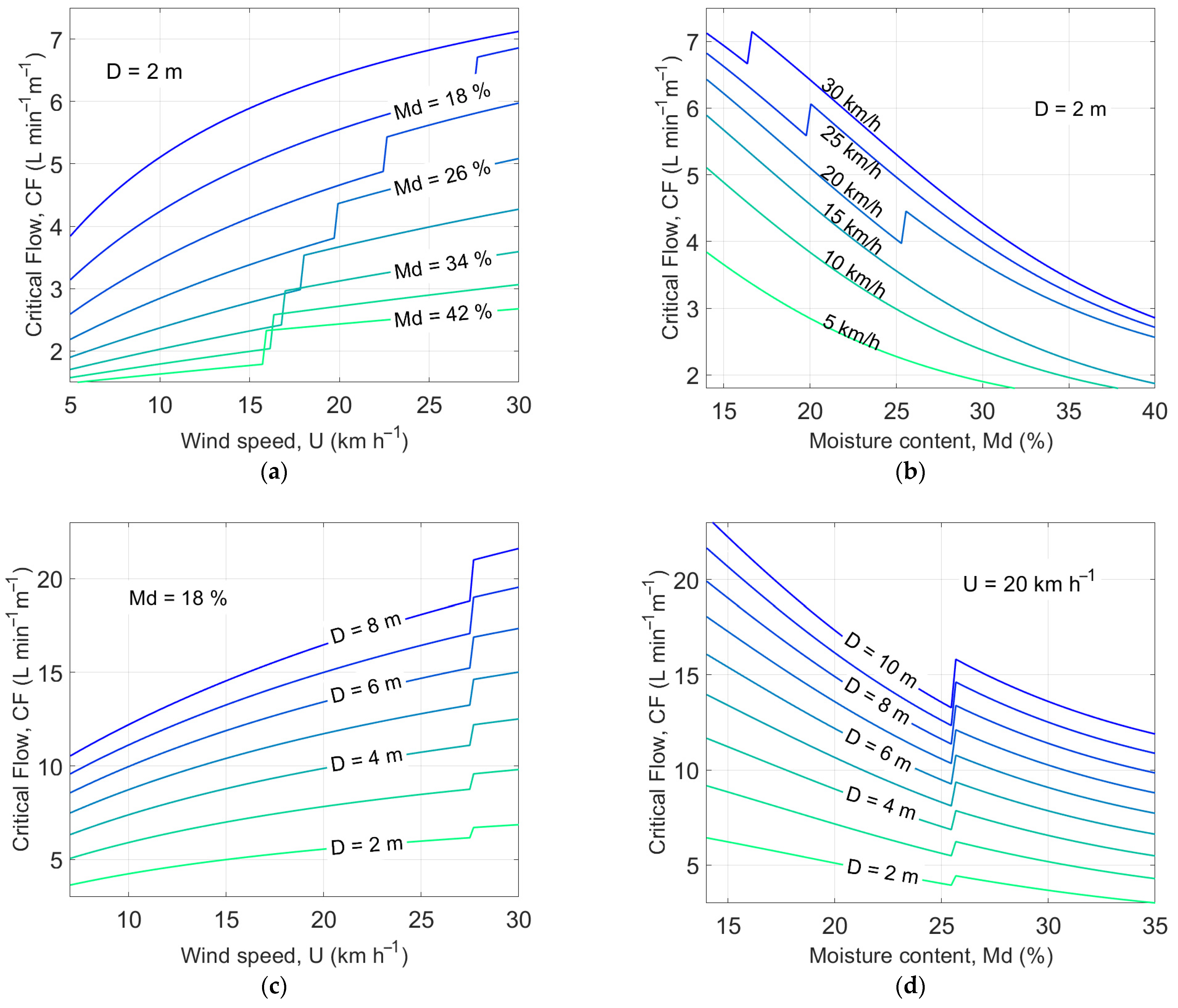
2.3. Critical Water Flow Rate CF as Function of Wind Speed and Moisture Content
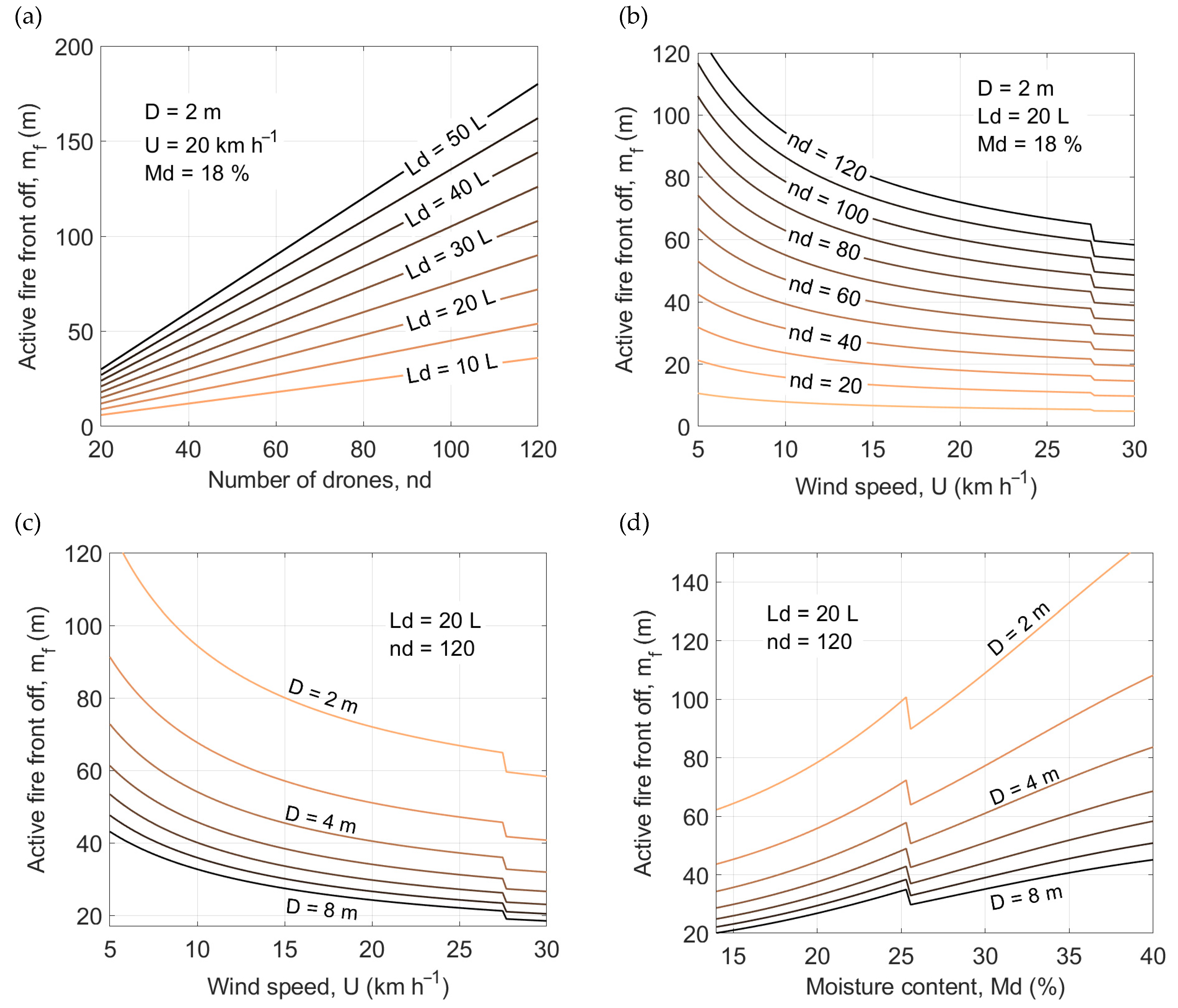
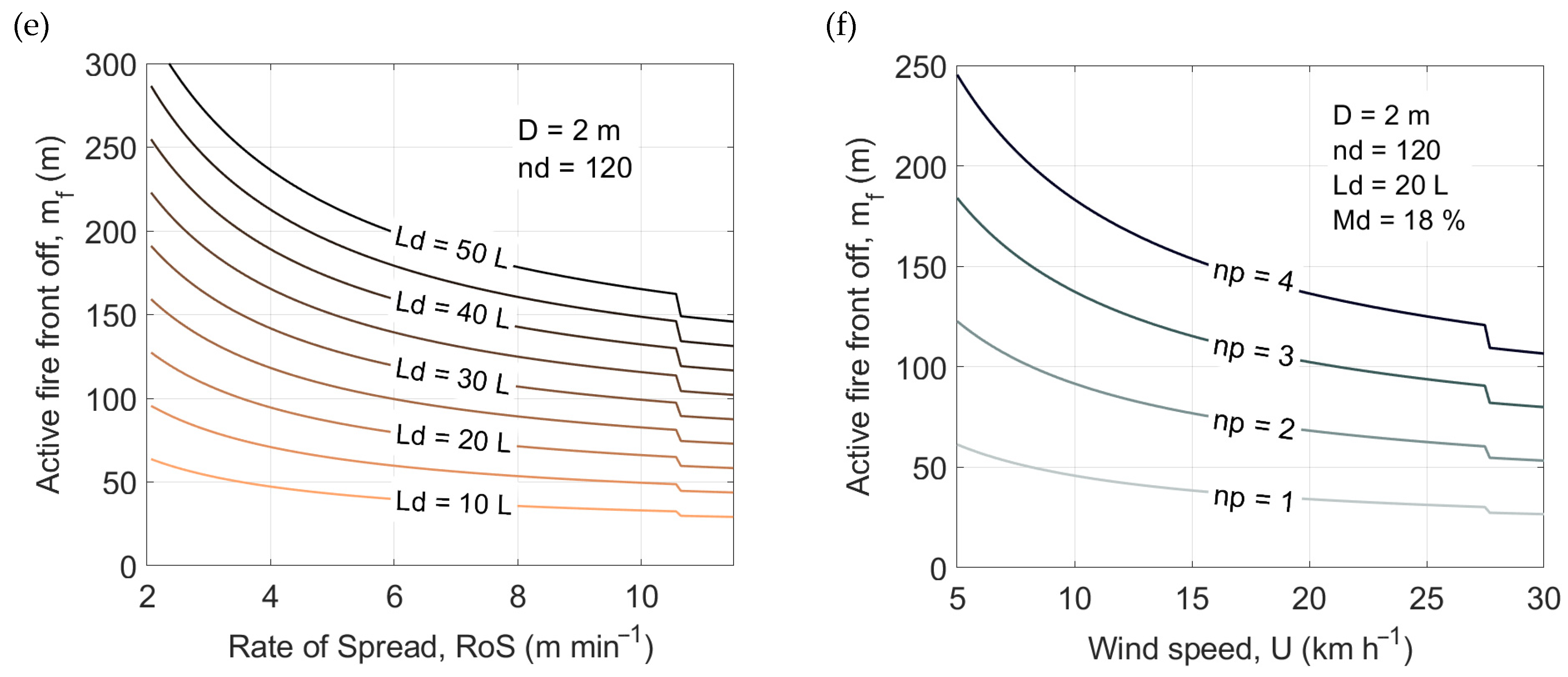
2.4. Impact of Drones on the Evolution of the Active Fire Front
2.5. Estimate of the Drones Required to Extinguish a Specified Number of Linear Meters of Active Fire Front
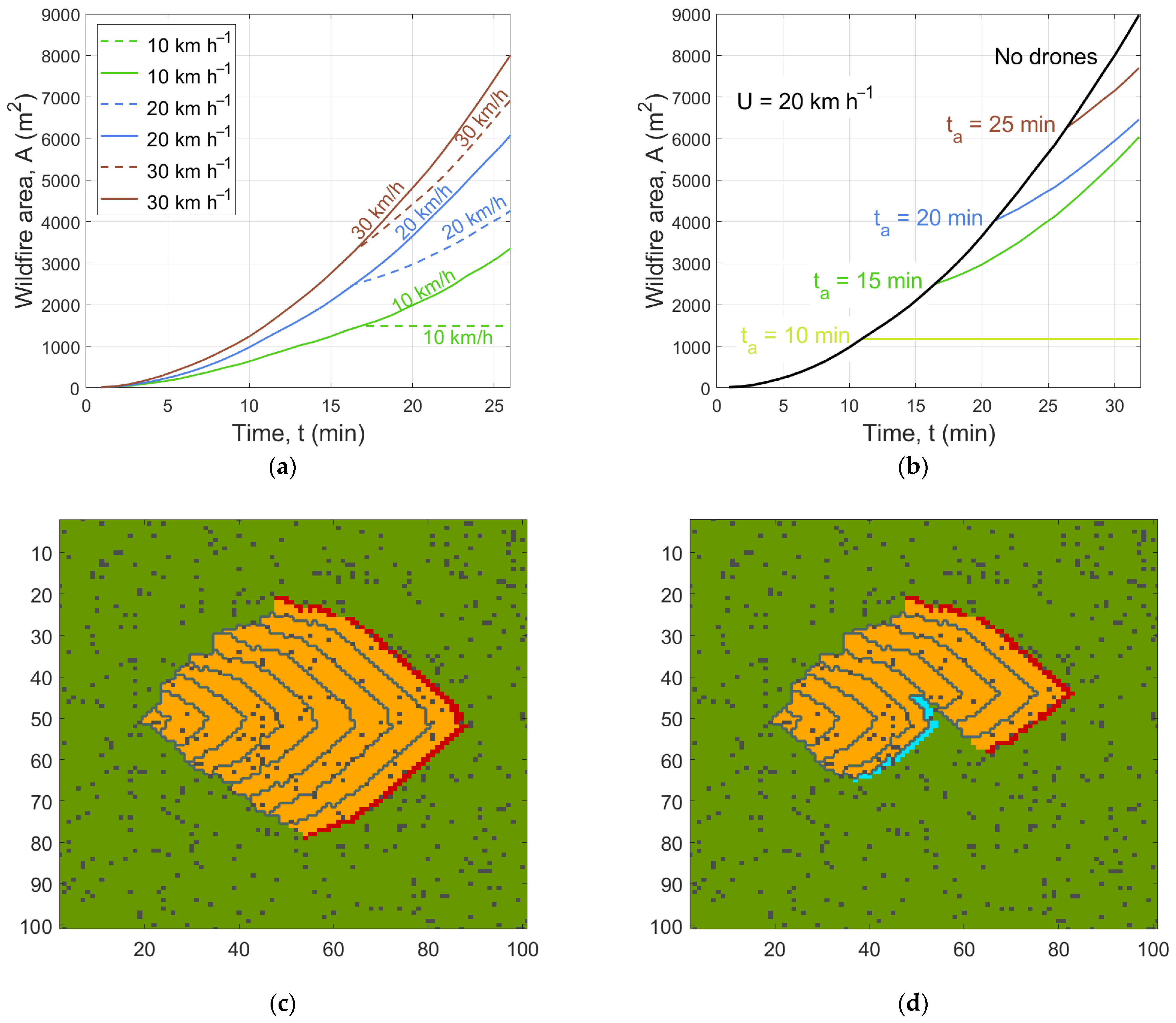
2.6. Cellular Automata Model for Studying the Effect of the UAV Platform on Fire Evolution
- . The cell cannot catch fire (empty cell). This state could describe cells corresponding to parts of the territory in which there is no vegetation that can burn.
- . The cell contains live fuel, not yet burned (tree cell).
- . The cell contains material that is burning (burning cell).
- . The cell contains completely burned fuel (burned cell).
- . The cell has a continuous flow of water that provides fire extinction ( computed in Section 2.2 and Section 2.3) thanks to the action of the drones.
- states that an empty cell maintains the same state without burning at next time step.
- states that if a cell contains vegetation fuel and there was at least one neighboring cell burning at the previous time step such that , it can catch fire with a probability greater than a certain threshold. As the wind speed increases, we also consider next-nearest cells as in [63,64]. In particular, we add two layers of cells for wind at and three for wind at .
- determines that a cell that is burning at the present moment will be completely burned at the next one. In subsequent times, it will no longer be able to spread the fire.
- implies that a previously burned cell remains burned.
3. Results and Discussion
3.1. Critical Flow Rate and Fire Front Linear Meters Arrested by Drones
3.2. Cellular Automata Model for Studying the Effect of the UAV Platform on Fire Evolution
4. Conclusions
5. Patents
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jolly, W.M.; Cochrane, M.A.; Freeborn, P.H.; Holden, Z.A.; Brown, T.J.; Williamson, G.J.; Bowman, D.M.J.S. Climate-Induced Variations in Global Wildfire Danger from 1979 to 2013. Nat. Commun. 2015, 6, 7537. [Google Scholar] [CrossRef]
- San-Miguel-Ayanz, J.; Moreno, J.M.; Camia, A. Analysis of Large Fires in European Mediterranean Landscapes: Lessons Learned and Perspectives. For. Ecol. Manag. 2013, 294, 11–22. [Google Scholar] [CrossRef]
- Caon, L.; Vallejo, V.R.; Ritsema, C.J.; Geissen, V. Effects of Wildfire on Soil Nutrients in Mediterranean Ecosystems. Earth Sci. Rev. 2014, 139, 47–58. [Google Scholar] [CrossRef]
- Cochrane, M.A. Fire Science for Rainforests. Nature 2003, 421, 913–919. [Google Scholar] [CrossRef]
- Moreira, F.; Viedma, O.; Arianoutsou, M.; Curt, T.; Koutsias, N.; Rigolot, E.; Barbati, A.; Corona, P.; Vaz, P.; Xanthopoulos, G.; et al. Landscape—Wildfire Interactions in Southern Europe: Implications for Landscape Management. J. Environ. Manag. 2011, 92, 2389–2402. [Google Scholar] [CrossRef]
- Martell, D.L. A Review of Recent Forest and Wildland Fire Management Decision Support Systems Research. Curr. For. Rep. 2015, 1, 128–137. [Google Scholar] [CrossRef]
- Fernandes, P.M. Fire-Smart Management of Forest Landscapes in the Mediterranean Basin under Global Change. Landsc. Urban Plan. 2013, 110, 175–182. [Google Scholar] [CrossRef]
- Leone, V.; Tedim, F.; McGee, T. Extreme Wildfire Events and Disasters; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Àgueda, A.; Pastor, E.; Planas, E. Different Scales for Studying the Effectiveness of Long-Term Forest Fire Retardants. Prog. Energy Combust. Sci. 2008, 34, 782–796. [Google Scholar] [CrossRef]
- Albini, F.A. An Overview of Research on Wildland Fire. Fire Saf. Sci. 1997, 5, 59–74. [Google Scholar] [CrossRef]
- Thompson, M.P.; Calkin, D.E.; Herynk, J.; McHugh, C.W.; Short, K.C. Airtankers and Wildfire Management in the US Forest Service: Examining Data Availability and Exploring Usage and Cost Trends. Int. J. Wildland Fire 2013, 22, 223–233. [Google Scholar] [CrossRef]
- Butler, B.W. Wildland Firefighter Safety Zones: A Review of Past Science and Summary of Future Needs. Int. J. Wildland Fire 2014, 23, 295–308. [Google Scholar] [CrossRef]
- Cascio, W.E. Wildland Fire Smoke and Human Health. Sci. Total Environ. 2018, 624, 586–595. [Google Scholar] [CrossRef]
- Extreme Wildfire Events and Disasters; Elsevier: Amsterdam, The Netherlands, 2020; ISBN 978-0-12-815721-3.
- Yuan, C.; Zhang, Y.; Liu, Z. A Survey on Technologies for Automatic Forest Fire Monitoring, Detection, and Fighting Using Unmanned Aerial Vehicles and Remote Sensing Techniques. Can. J. For. Res. 2015, 45, 783–792. [Google Scholar] [CrossRef]
- Floreano, D.; Wood, R.J. Science, Technology and the Future of Small Autonomous Drones. Nature 2015, 521, 460–466. [Google Scholar] [CrossRef]
- Al-Kaff, A.; Madridano, Á.; Campos, S.; García, F.; Martín, D.; de la Escalera, A. Emergency Support Unmanned Aerial Vehicle for Forest Fire Surveillance. Electronics 2020, 9, 260. [Google Scholar] [CrossRef]
- DOI Unmanned Aircraft Systems (UAS) Program—2018 Use Report. Available online: https://www.doi.gov/aviation/uas/news (accessed on 6 March 2021).
- Merino, L.; Caballero, F.; Martínez-de-Dios, J.R.; Maza, I.; Ollero, A. An Unmanned Aircraft System for Automatic Forest Fire Monitoring and Measurement. J. Intell. Robot. Syst. 2012, 65, 533–548. [Google Scholar] [CrossRef]
- Samiappan, S.; Hathcock, L.; Turnage, G.; McCraine, C.; Pitchford, J.; Moorhead, R. Remote Sensing of Wildfire Using a Small Unmanned Aerial System: Post-Fire Mapping, Vegetation Recovery and Damage Analysis in Grand Bay, Mississippi/Alabama, USA. Drones 2019, 3, 43. [Google Scholar] [CrossRef]
- Seraj, E.; Gombolay, M. Coordinated Control of UAVs for Human-Centered Active Sensing of Wildfires. In Proceedings of the 2020 American Control Conference (ACC), Online, 1–3 July 2020; pp. 1845–1852. [Google Scholar]
- Beachly, E.; Detweiler, C.; Elbaum, S.; Twidwell, D.; Duncan, B. UAS-Rx Interface for Mission Planning, Fire Tracking, Fire Ignition, and Real-Time Updating. In Proceedings of the 2017 IEEE International Symposium on Safety, Security and Rescue Robotics (SSRR), Shanghai, China, 11–13 October 2017; pp. 67–74. [Google Scholar]
- Shaffer, J.A.; Carrillo, E.; Xu, H. Hierarchal Application of Receding Horizon Synthesis and Dynamic Allocation for UAVs Fighting Fires. IEEE Access 2018, 6, 78868–78880. [Google Scholar] [CrossRef]
- Innocente, M.S.; Grasso, P. Swarm of Autonomous Drones Self-Organised to Fight the Spread of Wildfires. In Proceedings of the GEOSAFE Workshop on Robust Solutions for Fire Fighting (CEUR), L’Aquila, Italy, 19–20 July 2018. [Google Scholar]
- Innocente, M.S.; Grasso, P. Self-Organising Swarms of Firefighting Drones: Harnessing the Power of Collective Intelligence in Decentralised Multi-Robot Systems. J. Comput. Sci. 2019, 34, 80–101. [Google Scholar] [CrossRef]
- Soliman, A.M.S.; Cagan, S.C.; Buldum, B.B. The Design of a Rotary-Wing Unmanned Aerial Vehicles–Payload Drop Mechanism for Fire-Fighting Services Using Fire-Extinguishing Balls. SN Appl. Sci. 2019, 1, 1259. [Google Scholar] [CrossRef]
- Aydin, B.; Selvi, E.; Tao, J.; Starek, M.J. Use of Fire-Extinguishing Balls for a Conceptual System of Drone-Assisted Wildfire Fighting. Drones 2019, 3, 17. [Google Scholar] [CrossRef]
- Myeong, W.C.; Jung, K.Y.; Myung, H. Development of FAROS (Fire-Proof Drone) Using an Aramid Fiber Armor and Air Buffer Layer. In Proceedings of the 2017 14th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI), Jeju, Korea, 28 June–1 July 2017; pp. 204–207. [Google Scholar]
- Ma, Y.; Chiang, S.W.; Chu, X.; Li, J.; Gan, L.; Xu, C.; Yao, Y.; He, Y.; Li, B.; Kang, F.; et al. Thermal Design and Optimization of Lithium Ion Batteries for Unmanned Aerial Vehicles. Energy Storage 2019, 1, e48. [Google Scholar] [CrossRef]
- Legendre, D.; Becker, R.; Alméras, E.; Chassagne, A. Air Tanker Drop Patterns. Int. J. Wildland Fire 2014, 23, 272–280. [Google Scholar] [CrossRef]
- Volkov, R.S.; Kuznetsov, G.V.; Strizhak, P.A. Experimental Determination of the Fire-Break Size and Specific Water Consumption for Effective Containment and Complete Suppression of the Front Propagation of a Typical Local Wildfire. J. Appl. Mech. Tech. Phys. 2019, 60, 68–79. [Google Scholar] [CrossRef]
- Volkov, R.S.; Kuznetsov, G.V.; Strizhak, P.A. Extinguishing a Ground Forest Fire by Spraying Water Over Its Edge. J. Eng. Phys. Thermophys. 2018, 91, 758–765. [Google Scholar] [CrossRef]
- Vysokomornaya, O.V.; Kuznetsov, G.V.; Strizhak, P.A. Experimental Investigation of Atomized Water Droplet Initial Parameters Influence on Evaporation Intensity in Flaming Combustion Zone. Fire Saf. J. 2014, 70, 61–70. [Google Scholar] [CrossRef]
- Liu, Z.; Kim, A.K. A Review of Water Mist Fire Suppression Systems—Fundamental Studies. J. Fire Prot. Eng. 1999, 10, 32–50. [Google Scholar] [CrossRef]
- Williams, A.; Yakimenko, O. Persistent Mobile Aerial Surveillance Platform Using Intelligent Battery Health Management and Drone Swapping. In Proceedings of the 2018 4th International Conference on Control, Automation and Robotics (ICCAR), Auckland, New Zealand, 20–23 April 2018; pp. 237–246. [Google Scholar]
- Ullah, H.; Nair, N.G.; Moore, A.; Nugent, C.; Muschamp, P.; Cuevas, M. 5G Communication: An Overview of Vehicle-to-Everything, Drones, and Healthcare Use-Cases. IEEE Access 2019, 7, 37251–37268. [Google Scholar] [CrossRef]
- Hildmann, H.; Kovacs, E.; Saffre, F.; Isakovic, A.F. Nature-Inspired Drone Swarming for Real-Time Aerial Data-Collection Under Dynamic Operational Constraints. Drones 2019, 3, 71. [Google Scholar] [CrossRef]
- Majd, A.; Loni, M.; Sahebi, G.; Daneshtalab, M. Improving Motion Safety and Efficiency of Intelligent Autonomous Swarm of Drones. Drones 2020, 4, 48. [Google Scholar] [CrossRef]
- Grant, G.; Brenton, J.; Drysdale, D. Fire Suppression by Water Sprays. Prog. Energy Combust. Sci. 2000, 26, 79–130. [Google Scholar] [CrossRef]
- Hansen, R. Estimating the Amount of Water Required to Extinguish Wildfires under Different Conditions and in Various Fuel Types. Int. J. Wildland Fire 2012, 21, 525. [Google Scholar] [CrossRef]
- Penney, G.; Habibi, D.; Cattani, M.; Carter, M. Calculation of Critical Water Flow Rates for Wildfire Suppression. Fire 2019, 2, 3. [Google Scholar] [CrossRef]
- Rasbash, D.J. The Extinction of Fire with Plain Water: A Review. Fire Saf. Sci. 1986, 1, 1145–1163. [Google Scholar] [CrossRef]
- Beyler, C. A Unified Model of Fire Suppression by. J. Fire Prot. Eng. 2016, 4, 5–16. [Google Scholar] [CrossRef]
- Spalding, D.B. Some Fundamentals of Combustion; Butterworths Scientific Publications: London, UK, 1955. [Google Scholar]
- Albini, F.A. A Model for the Wind-Blown Flame from a Line Fire. Combust. Flame 1981, 43, 155–174. [Google Scholar] [CrossRef]
- Chandler, C.; Cheney, P.; Thomas, P.; Trabaud, L.; Williams, D. Fire in Forestry. Volume 1. Forest Fire Behavior and Effects. Volume 2. Forest Fire Management and Organization; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1983. [Google Scholar]
- Byram, G.M. Combustion of Forest Fuels. In Forest Fire: Control and Use; Davis, K.P., Ed.; McGraw Hill: New York, NY, USA, 1959. [Google Scholar]
- Martins Fernandes, P.A. Fire Spread Prediction in Shrub Fuels in Portugal. For. Ecol. Manag. 2001, 144, 67–74. [Google Scholar] [CrossRef]
- Preisler, H.; Ager, A. Forest-Fire Models. Encycl. Environ. 2013, 3, 2181–2185. [Google Scholar] [CrossRef]
- Wolfram, S. Statistical Mechanics of Cellular Automata. Rev. Mod. Phys. 1983, 55, 601–644. [Google Scholar] [CrossRef]
- Karafyllidis, I.; Thanailakis, A. A Model for Predicting Forest Fire Spreading Using Cellular Automata. Ecol. Model. 1997, 99, 87–97. [Google Scholar] [CrossRef]
- Ferragut, L.; Monedero, S.; Asensio, M.I.; Ramírez, J. Scientific Advances in Fire Modelling and Its Integration in a Forest Fire Decision System. WIT Trans. Ecol. Environ. 2008, 119, 31–38. [Google Scholar] [CrossRef]
- Dumond, Y. An Applied Step in Forest Fire Spread Modelling. In Proceedings of the ECMS 2009, Madrid, Spain, 9–12 June 2009; Otamendi, J., Bargiela, A., Montes, J.L., Doncel Pedrera, L.M., Eds.; pp. 32–38. [Google Scholar]
- Yassemi, S.; Dragićević, S.; Schmidt, M. Design and Implementation of an Integrated GIS-Based Cellular Automata Model to Characterize Forest Fire Behaviour. Ecol. Model. 2008, 210, 71–84. [Google Scholar] [CrossRef]
- Gaudreau, J.; Perez, L.; Drapeau, P. BorealFireSim: A GIS-Based Cellular Automata Model of Wildfires for the Boreal Forest of Quebec in a Climate Change Paradigm. Ecol. Inform. 2016, 32, 12–27. [Google Scholar] [CrossRef]
- Russo, L.; Russo, P.; Siettos, C.I. A Complex Network Theory Approach for the Spatial Distribution of Fire Breaks in Heterogeneous Forest Landscapes for the Control of Wildland Fires. PLoS ONE 2016, 11, e0163226. [Google Scholar] [CrossRef]
- Trunfio, G.A. Predicting Wildfire Spreading Through a Hexagonal Cellular Automata Model. In Proceedings of the Cellular Automata for Research and Industry, Amsterdam, The Netherlands, 25–28 October 2004; Sloot, P.M.A., Chopard, B., Hoekstra, A.G., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 385–394. [Google Scholar]
- Hernández Encinas, L.; Hoya White, S.; Martín del Rey, A.; Rodríguez Sánchez, G. Modelling Forest Fire Spread Using Hexagonal Cellular Automata. Appl. Math. Model. 2007, 31, 1213–1227. [Google Scholar] [CrossRef]
- Albinet, G.; Searby, G.; Stauffer, D. Fire Propagation in a 2-D Random Medium. J. Phys. 1986, 47, 1–7. [Google Scholar] [CrossRef]
- Trunfio, G.A.; D′Ambrosio, D.; Rongo, R.; Spataro, W.; Di Gregorio, S. A New Algorithm for Simulating Wildfire Spread through Cellular Automata. ACM Trans. Model. Comput. Simul. 2011, 22, 1–26. [Google Scholar] [CrossRef]
- Alexandridis, A.; Vakalis, D.; Siettos, C.I.; Bafas, G.V. A Cellular Automata Model for Forest Fire Spread Prediction: The Case of the Wildfire That Swept through Spetses Island in 1990. Appl. Math. Comput. 2008, 204, 191–201. [Google Scholar] [CrossRef]
- Alexandridis, A.; Russo, L.; Vakalis, D.; Bafas, G.V.; Siettos, C.I. Wildland Fire Spread Modelling Using Cellular Automata: Evolution in Large-Scale Spatially Heterogeneous Environments under Fire Suppression Tactics. Int. J. Wildland Fire 2011, 20, 633. [Google Scholar] [CrossRef]
- Bodrožić, L.; Stipaničev, D.; Šerić, M. Forest fires spread modeling using cellular automata approach. Mod. Trends Control 2006, 23–33. [Google Scholar]
- Freire, J.G.; DaCamara, C.C. Using Cellular Automata to Simulate Wildfire Propagation and to Assist in Fire Management. Nat. Hazards Earth Syst. Sci. 2019, 19, 169–179. [Google Scholar] [CrossRef]
- Santoni, P.A.; Simeoni, A.; Rossi, J.L.; Bosseur, F.; Morandini, F.; Silvani, X.; Balbi, J.H.; Cancellieri, D.; Rossi, L. Instrumentation of Wildland Fire: Characterisation of a Fire Spreading through a Mediterranean Shrub. Fire Saf. J. 2006, 41, 171–184. [Google Scholar] [CrossRef]
- Santoni, P.A.; Morandini, F.; Barboni, T. Steady and Unsteady Fireline Intensity of Spreading Fires at Laboratory Scale. Open Thermodyn. J. 2010, 4, 212–219. [Google Scholar] [CrossRef]
- Tihay, V.; Santoni, P.-A.; Simeoni, A.; Garo, J.-P.; Vantelon, J.-P. Skeletal and Global Mechanisms for the Combustion of Gases Released by Crushed Forest Fuels. Combust. Flame 2009, 156, 1565–1575. [Google Scholar] [CrossRef][Green Version]
- Tihay-Felicelli, V.; Santoni, P.-A.; Barboni, T.; Leonelli, L. Autoignition of Dead Shrub Twigs: Influence of Diameter on Ignition. Fire Technol. 2016, 52, 897–929. [Google Scholar] [CrossRef]
- Padhi, S.; Shotorban, B.; Mahalingam, S. Computational Investigation of Flame Characteristics of a Non-Propagating Shrub Fire. Fire Saf. J. 2016, 81, 64–73. [Google Scholar] [CrossRef]
- Penney, G.; Habibi, D.; Cattani, M. Firefighter Tenability and Its Influence on Wildfire Suppression. Fire Saf. J. 2019, 106, 38–51. [Google Scholar] [CrossRef]
- Alessandri, A.; Bagnerini, P.; Gaggero, M.; Mantelli, L. Parameter Estimation of Fire Propagation Models Using Level Set Methods. Appl. Math. Model. 2021, 92, 731–747. [Google Scholar] [CrossRef]
- Ghio, M. Methods and Apparatus for the Employment of Drones in Firefighting Activities. Patent WO2017208272A1, 31 May 2016. [Google Scholar]

| Drone | Company | Type | Weight (kg) | Dimensions (mm) | Folded Dimensions (mm) | Propeller/ Rotor Number | Speed (km/h) | Payload (kg) | Flight Time (min) | Website |
|---|---|---|---|---|---|---|---|---|---|---|
| PD6B-type2 | Prodrone | hexacopter | 19.5 (4 batteries included) | L 1874 W 2060 H 474 | L 1348 W 600 H 474 | 6 | max 60 | No payload | 35 | prodrone.com |
| 10 | 15 | |||||||||
| 20 (practical use) | 10 | |||||||||
| GD-40X | Gryphon | X8 octocopter | 12 (dry weight) 40 (max takeoff weight) | D 1400 | D 1000 detachable arms retractable gear | 8 (4 + 4) coaxial propellers | max 50 avg 40 | No payload | 50 | gryphondynamics.co.kr |
| 22–25 | 24 | |||||||||
| Vulcan D8 | Vulcan | X8 octocopter | 16 (dry weight) max 55 | L 1400 W 1150 D 1670 | L 1400 W 400 h 500 | 8 (4 + 4) coaxial propellers | max 80 avg 30/40 | No payload | >30 | vulcanuav.com |
| 10 | 22 | |||||||||
| 20 | 14 | |||||||||
| Griff 135 | Griff Aviation | X8 octocopter | max takeoff weight 135 | L 2410 W 2260 H 470 | L 1440 W 770 H 470 | 8 (4 + 4) coaxial propellers | — | No payload | >30 | griffaviation.com |
| 30 (max 50) | 25–30 |
| Drone | Company | Type | Speed (km/h) | Payload (kg) | Website |
|---|---|---|---|---|---|
| Pegasus 120 | Israel’s Aeronautics | octacopter | 80 | 45 | cp-aeronautics.com |
| Altinay Albatros | Altinay | CAV | - | 50–100–150 | altinay-advanced.com |
| EHANG 216 | Ehang AAV | AAV | 130 | 220 | ehang.com |
| Griff 300 | Griff Aviation | X8 octocopter | 60 (avg 50) | 226 | griffaviation.com |
| Symbol | Parameter | Value | References |
|---|---|---|---|
| effective heat of combustion | 19,500 | [65] | |
| heat of gasification of the fuel | 1800 | [40] | |
| convective heat transfer coefficient | 20 | [40] | |
| specific heat of air at constant pressure | 1 | [40] | |
| oxygen mass fraction | 0.233 | [40] | |
| heat of combustion per unit mass of oxygen consumed (Genista salzmannii) | 13,480 | [66] | |
| fractional convective heat loss | 0.3 | [40] | |
| efficiency of water application | 0.7 | [40] | |
| enthalpy change of water | 2640 | [40] | |
| atmospheric transmissivity | 1 | [40] | |
| radiative component per unit length of fire front (Erica arborea) | 0.20 | [67] | |
| fuel emissivity | 0.6 | [40] | |
| Stefan-Boltzmann constant | [40] | ||
| fuel surface temperature (Cistus monspeliensis) | 693 | [68] | |
| gas temperature | 800 | [69] | |
| ambient temperature | 293 | [40] | |
| total fuel load | 15 | [41] | |
| active flame depth | [40,41] |
| Parameter | Symbol | Value |
|---|---|---|
| Rate of spread parameters | 3.258 | |
| 0.958 | ||
| 0.111 |
| Values for the probabilityand parameter | ||
| Grass | Shrub | |
| 0.4 | 0.4 | |
| 0.18 | 0.24 | |
| Values for the probability | ||
| Category | Density | |
| Sparse | −0.4 | |
| Normal | 0 | |
| Dense | 0.3 | |
| Operational parameters for CA simulations | ||
| Parameter | Symbol | Value |
| Spread probability under no wind and flat terrain | 0.6 | |
| Wind parameter 1 | 0.045 | |
| Wind parameter 2 | 0.131 | |
| Moisture parameter | 0.111 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ausonio, E.; Bagnerini, P.; Ghio, M. Drone Swarms in Fire Suppression Activities: A Conceptual Framework. Drones 2021, 5, 17. https://doi.org/10.3390/drones5010017
Ausonio E, Bagnerini P, Ghio M. Drone Swarms in Fire Suppression Activities: A Conceptual Framework. Drones. 2021; 5(1):17. https://doi.org/10.3390/drones5010017
Chicago/Turabian StyleAusonio, Elena, Patrizia Bagnerini, and Marco Ghio. 2021. "Drone Swarms in Fire Suppression Activities: A Conceptual Framework" Drones 5, no. 1: 17. https://doi.org/10.3390/drones5010017
APA StyleAusonio, E., Bagnerini, P., & Ghio, M. (2021). Drone Swarms in Fire Suppression Activities: A Conceptual Framework. Drones, 5(1), 17. https://doi.org/10.3390/drones5010017





