Generic Component-Based Mission-Centric Energy Model for Micro-Scale Unmanned Aerial Vehicles
Abstract
:1. Introduction
2. State of the Art
3. Model
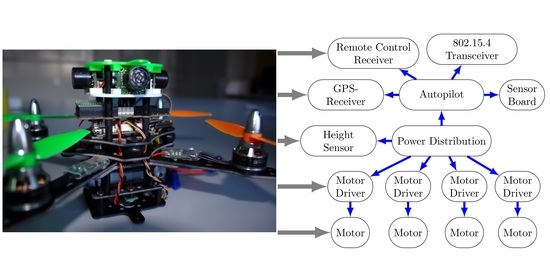
3.1. Components of a Quadcopter
3.2. Description of Quadcopter Missions
3.3. Power Function of Components
3.4. Machine Learning Approaches for Power Functions
- White-Box
- This approach uses specific system knowledge to determine the necessary coefficients based on the physics of the system. Such approaches rely on either the electrical, dynamic or fluid system theory and the known behaviour of the component. Very few data are necessary for the approach, but it generally lacks in precision, because some effects are not modelled or some coefficients are hard to measure.
- Black-Box
- This approach views the component as a black box. The coefficients of the power functions of different components are fitted to the data using machine learning techniques like regressions, gradient descent or evolutionary algorithms. These aim to minimise in the learning process. The used models are typically neural networks or genetic programming. All these methods typically need a large amount of data from a sufficient set of environmental conditions to guarantee stable results. Additionally, hyperparameters need to be chosen manually by the user.
- Grey-Box
- This approach combines the first two approaches. It uses system knowledge to derive analytical power function with unknown coefficients from the behaviour of the component using expert knowledge. Afterwards, the coefficients are fitted to experimental data to parametrise the model. This approach needs far less experimental data than the black-box approach, but still enables adaptation to real hardware.
3.5. An Energy Model for the FINken Quadcopters
4. Experiments
4.1. Experimental Set-Up
4.2. Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CNN | Convolutional Neural Network |
| IMU | Inertial Measurement Unit |
| GPS | Global Positioning System |
| LED | Light Emitting Diode |
| SD-Card | Secure Digital Card |
| UAV | Unmanned Aerial Vehicle |
| PSO | Particle Swarm Optimisation |
| ADC | Analogue Digital Converter |
| LiPo | Lithium-Polymer Battery |
References
- Seo, J.; Duque, L.; Wacker, J. Drone-enabled bridge inspection methodology and application. Autom. Constr. 2018, 94, 112–126. [Google Scholar] [CrossRef]
- Shihavuddin, A.; Chen, X.; Fedorov, V.; Nymark Christensen, A.; Andre Brogaard Riis, N.; Branner, K.; Bjorholm Dahl, A.; Reinhold Paulsen, R. Wind turbine surface damage detection by deep learning aided drone inspection analysis. Energies 2019, 12, 676. [Google Scholar] [CrossRef] [Green Version]
- Dorigo, M.; Floreano, D.; Gambardella, L.M.; Mondada, F.; Nolfi, S.; Baaboura, T.; Birattari, M.; Bonani, M.; Brambilla, M.; Brutschy, A.; et al. Swarmanoid: A novel concept for the study of heterogeneous robotic swarms. IEEE Robot. Autom. Mag. 2013, 20, 60–71. [Google Scholar] [CrossRef] [Green Version]
- Steup, C.; Mai, S.; Mostaghim, S. Evaluation Platform for Micro Aerial Indoor Swarm Robotics; Technical Report FIN-003-2016; Otto-von-Guericke-Universität Magdeburg: Magdeburg, Germany, 2016. [Google Scholar]
- Zelazo, D.; Franchi, A.; Bülthoff, H.H.; Robuffo Giordano, P. Decentralized rigidity maintenance control with range measurements for multi-robot systems. Int. J. Robot. Res. 2015, 34, 105–128. [Google Scholar] [CrossRef] [Green Version]
- Stirling, T.; Roberts, J.; Zufferey, J.C.; Floreano, D. Indoor navigation with a swarm of flying robots. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 4641–4647. [Google Scholar]
- Erdelj, M.; Król, M.; Natalizio, E. Wireless Sensor Networks and Multi-UAV systems for natural disaster management. Comput. Netw. 2017, 124, 72–86. [Google Scholar] [CrossRef]
- Jatmiko, W.; Jovan, F.; Dhiemas, R.; Sakti, A.M.; Ivan, F.M.; Fukuda, T.; Sekiyama, K. Robots implementation for odor source localization using PSO algorithm. WSEAS Trans. Circuits Syst. 2011, 10, 115–125. [Google Scholar]
- Marchant, W.; Tosunoglu, S. Rethinking Wildfire Suppression With Swarm Robotics. In Proceedings of the FCRAR 2016 29th Florida Conference on Recent Advances In Robotics, Miami, FL, USA, 12–13 May 2016; pp. 186–191. [Google Scholar]
- Bayat, B.; Crasta, N.; Crespi, A. Environmental Monitoring using Autonomous Vehicles: A Survey of Recent Searching Techniques. Curr. Opin. Biotechnol. 2017, 45, 76–84. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bayındır, L. A review of swarm robotics tasks. Neurocomputing 2016, 172, 292–321. [Google Scholar] [CrossRef]
- Khaldi, B.; Cherif, F. An Overview of Swarm Robotics: Swarm Intelligence Applied to Multi-robotics. Int. J. Comput. Appl. 2015, 126, 31–37. [Google Scholar] [CrossRef]
- Mostaghim, S.; Steup, C.; Witt, F. Energy Aware Particle Swarm Optimization as Search Mechanism for Aerial Micro-robots. In Proceedings of the 2016 IEEE Symposium Series on Computational Intelligence (SSCI), Athens, Greece, 6–9 December 2016. [Google Scholar]
- Bartashevich, P.; Koerte, D.; Mostaghim, S. Energy-Saving Decision Making for Aerial Swarms: PSO-based Navigation in Vector Fields. In Proceedings of the 2017 IEEE Symposium Series on Computational Intelligence (SSCI), Honolulu, HI, USA, 27 November–1 December 2017; pp. 1848–1855. [Google Scholar]
- Mai, S.; Zille, H.; Steup, C.; Mostaghim, S. Multi-Objective Collective Search and Movement-based Metrics in Swarm Robotics. In Proceedings of the Genetic and Evolutionary Computation Conference Companion (GECCO), Prague, Czech Republic, 13–17 July 2019; pp. 387–388. [Google Scholar]
- Dietrich, T.; Krug, S.; Zimmermann, A. An Empirical Study on Generic Multicopter Energy Consumption Profiles. In Proceedings of the 2017 Annual IEEE International Systems Conference (SysCon), Montreal, QC, Canada, 24–27 April 2017; IEEE: Montreal, QC, Canada, 2017; pp. 406–411. [Google Scholar]
- Di Franco, C.; Buttazzo, G. Energy-aware coverage path planning of UAVs. In Proceedings of the 2015 IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC), Vila Real, Portugal, 8–10 April 2015; pp. 111–117. [Google Scholar]
- Abdilla, A.; Richards, A.; Burrow, S. Power and endurance modelling of battery-powered rotorcraft. IEEE Int. Conf. Intell. Robot. Syst. 2015, 2015, 675–680. [Google Scholar]
- Roberts, J.F.; Zufferey, J.C.; Floreano, D. Energy management for indoor hovering robots. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, IROS, Nice, France, 22–26 September 2008; pp. 1242–1247. [Google Scholar]
- Yacef, F.; Rizoug, N.; Bouhali, O.; Hamerlain, M. Optimization of Energy Consumption for Quadrotor. In Proceedings of the 2017 Internation Micro Air Vehicle Conference and Flight Competition (IMAV), Madrid, Spain, 30 September–4 October 2017; IMAV: Toulouse, France, 2017; pp. 215–222. [Google Scholar]
- Hoyer, L.; Steup, C.; Mostaghim, S. A Robot Localization Framework Using CNNs for Object Detection and Pose Estimation. In Proceedings of the IEEE Symposium Series on Computational Intelligence (SSCI), Bangalore, India, 18–21 November 2018; IEEE: Bangalore, India, 2018; pp. 1388–1395. [Google Scholar]




| Figure | Parameter | Value in W | Standard Deviation |
|---|---|---|---|
| Figure 2a | 1.52 | 0.0037 | |
| Figure 2b | 4.60 | 0.0082 | |
| Figure 2c | 9.33 | 0.0113 | |
| Figure 2d | 0.63 | 0.0135 | |
| Figure 2e | 0.84 | 0.0095 | |
| Figure 2f | 0.13 | 0.0001 | |
| Figure 2f | 0.47 | 0.0003 |
| Training | Flight 1 Comb | Flight 2 Comb | Flight 3 Comb | Flight 1 Hover | Flight 2 Hover | Flight 1 Horiz | Flight 2 Horiz | Flight 1 Vertical |
|---|---|---|---|---|---|---|---|---|
| mean | 0.0462 | 0.0345 | 0.0851 | 0.0095 | 0.0177 | 0.0273 | 0.0705 | 0.0270 |
| std | 0.0322 | 0.0180 | 0.0279 | 0.0055 | 0.0043 | 0.0186 | 0.0176 | 0.0152 |
| 25%-quantile | 0.0153 | 0.0197 | 0.0721 | 0.0044 | 0.0153 | 0.0119 | 0.0656 | 0.0139 |
| 50%-quantile | 0.0410 | 0.0351 | 0.0992 | 0.0093 | 0.0173 | 0.0222 | 0.0758 | 0.0309 |
| 75%-quantile | 0.0759 | 0.0529 | 0.1038 | 0.0146 | 0.0211 | 0.0434 | 0.0810 | 0.0410 |
| max | 0.1018 | 0.0607 | 0.1106 | 0.0199 | 0.0263 | 0.0640 | 0.0902 | 0.0478 |
| 1.5313 | 0.1860 | 1.9742 | 0.0719 | 0.8129 | 0.8801 | 0.8100 | 0.0008 |
| Validation | Flight 1 | Flight 2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Model | Hover | Vert | Horiz | Comb | Hover | Vert | Horiz | Comb |
| mean | 0.0866 | 0.2231 | 0.0280 | 0.0362 | 0.0218 | 0.1087 | 0.0367 | 0.0186 |
| std | 0.0728 | 0.2311 | 0.0164 | 0.0277 | 0.0121 | 0.1188 | 0.0104 | 0.0076 |
| 25%-quantile | 0.0128 | 0.0126 | 0.0151 | 0.0181 | 0.0121 | 0.0132 | 0.0341 | 0.0124 |
| 50%-quantile | 0.0699 | 0.0675 | 0.0286 | 0.0253 | 0.0220 | 0.0305 | 0.0391 | 0.0199 |
| 75%-quantile | 0.1487 | 0.4287 | 0.0377 | 0.0542 | 0.0322 | 0.2346 | 0.0437 | 0.0249 |
| max | 0.2284 | 0.6310 | 0.0686 | 0.1046 | 0.0448 | 0.3544 | 0.0502 | 0.0315 |
| 4.4622 | 12.4032 | 1.3300 | 2.0428 | 0.9950 | 10.3208 | 1.3155 | 0.4166 | |
| Validation | Flight 1 | Flight 2 | Flight 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | Hover | Vert | Comb | Hover | Vert | Comb | Hover | Vert | Comb |
| mean | 0.0456 | 0.0116 | 0.0317 | 0.0597 | 0.1127 | 0.1024 | 0.0555 | 0.0964 | 0.1373 |
| std | 0.0294 | 0.0077 | 0.0218 | 0.0197 | 0.0353 | 0.0313 | 0.0281 | 0.0509 | 0.0712 |
| max | 0.1306 | 0.0293 | 0.0648 | 0.0833 | 0.1670 | 0.1504 | 0.1094 | 0.1588 | 0.2340 |
| 2.7085 | 0.3777 | 1.2639 | 0.1630 | 3.1661 | 3.2976 | 2.1741 | 4.1327 | 6.3156 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steup, C.; Parlow, S.; Mai, S.; Mostaghim, S. Generic Component-Based Mission-Centric Energy Model for Micro-Scale Unmanned Aerial Vehicles. Drones 2020, 4, 63. https://doi.org/10.3390/drones4040063
Steup C, Parlow S, Mai S, Mostaghim S. Generic Component-Based Mission-Centric Energy Model for Micro-Scale Unmanned Aerial Vehicles. Drones. 2020; 4(4):63. https://doi.org/10.3390/drones4040063
Chicago/Turabian StyleSteup, Christoph, Simon Parlow, Sebastian Mai, and Sanaz Mostaghim. 2020. "Generic Component-Based Mission-Centric Energy Model for Micro-Scale Unmanned Aerial Vehicles" Drones 4, no. 4: 63. https://doi.org/10.3390/drones4040063
APA StyleSteup, C., Parlow, S., Mai, S., & Mostaghim, S. (2020). Generic Component-Based Mission-Centric Energy Model for Micro-Scale Unmanned Aerial Vehicles. Drones, 4(4), 63. https://doi.org/10.3390/drones4040063