Virtual Modelling and Testing of the Single and Contra-Rotating Co-Axial Propeller

Abstract

Propellers are a vital component to achieve successful and reliable operation of drones. However, the drone developer faces many challenges while selecting a propeller and a common approach is to perform static thrust measurement. However, the selection of a propeller using a static thrust measurement system is time-consuming. To overcome a need for the static thrust system a virtual model has been developed for measuring both the static and dynamic thrust of a single and coaxial propeller. The virtual model is reliable enough to minimize the need for full-scale tests. The virtual model has been built using two open-source software Qblade and OpenFoam. Qblade is employed to obtain the lift and drag coefficients of the propeller’s airfoil section. OpenFoam is utilized to perform the flow simulations of propellers and for obtaining the thrust and torque data of the propeller. The developed virtual model is validated with experimental data and the experimental data are obtained by developing a multi-force balance system for measuring thrusts and torques of a single and a pair of coaxial contra-rotating propellers. The data obtained from the propeller virtual model are compared with the measurement data. For a single propeller, the virtual model shows that the estimated forces are close to the experiment at lower rotational speeds. For coaxial propellers, there are some deviations at the rear propeller due to the turbulence and flow disturbance caused by the front propeller. However, the computed thrust data are still accurate enough to be used in selecting the propeller. The studies indicate that in the future, these virtual models will minimize a need for experimental testing.

1. Introduction

The sales of drones have steeply increased lately and there are many developments around the drone technology. Like a lot of common technology, drones came from the military sector, but they have been used in many civilian applications. Drones often vary widely in their configurations depending on the platform and mission. There are different classifications for drones based on different parameters. An excellent review to identify a novel classification of flying drones that range from unmanned air vehicles to smart dust, with their newly defined applications have been conducted by Hassanalian and Abdelkefi [1].

Nowadays the three main users are, by order of importance the government, the consumers, and finally the commercial area. However, the commercial sector has the potential to overtake the consumer market. Indeed, it is only the beginning of the use of the drones by the business but the Unmanned Aerial Vehicles (UAVs) already have a wide range of applications: construction, agriculture, offshore oil/gas and refining, real estate, pipelines inspection, cinematography, etc. The prospects of drone technology are considerable and it has already been used in many applications such as medical, powerline inspection, surveying, transport, logistics, and plant inspection. Sevendof AS AS (https://www.sevendof.com/) is developing a drone for powerline application and the drone has to cover long distances with low specific fuel consumption and one of the challenges is to identify a suitable propeller that consumes less power and provides enough performance to complete the mission. One of the challenges while designing and manufacturing a drone is to identify the most suitable propeller that meets all the mission requirements. As per today, the drone developer has to buy several propellers and test them one by one to identify the best propeller. Mostly static testing methods, to measure the static thrust, are employed to qualify the propeller and dynamic thrust measurements are not performed. Both dynamic and static thrust measurement methods are expensive and time-consuming. That is why it is important to develop virtual models that can substitute for a major part of the physical tests. [2,3].

A simplified approach to estimate the thrust of the propeller which is based on the wind speed, thrust coefficient, propeller diameter, and rotation rate, but this approach neglects rotor drag during the forward flight [4], which is a very important parameter. Furthermore, the accuracy of the simplified model deteriorates during the forward flight conditions, particularly at high speed and high pitch flight. Knowing the limitation of these models is extremely important for creating a suitable flight dynamic model. The static thrust measurements of the propeller in absence of wind can be performed using several open-source simulation tools e.g. Qprop, JavaProp, JBlade. However, these tools cannot be employed for a drone that is operating and hovering in strong headwinds or designed to be most efficient at higher forward flight. The other approach proposed by Hoffmann et al. [5] requires that the mechanical power of each propeller be known. However, this approach requires current sensing on each motor which can lead to bulky electronics and requires an accurate electrical to mechanical efficiency model [6]. To overcome some of the challenges associated with these methods, a method based on blade element theory (BET) was developed to analyze the propeller performance [7,8]. The BET approach was later on modified and was combined with blade element momentum theory (BEMT) to model rotor thrust in the axial climb with small-angle approximations. However, this model becomes inaccurate during the forward flight. Another modelling approach for estimating the thrust, drag, and torque of propellers used in the UAV applications for hover and high- speed forward flight regimes was proposed by Gill and D’Andrea [6]. In their approach, the propeller model was created using both Blade Element Theory (BET) and Blade Element Momentum Theory (BEMT). The approach was applied to three different types of propellers to showcase its versatility and this approach can accurately predict the rotor forces. They found that the induced drag has not occurred on the blade element except at the very tip of the propeller blade. Hence, they suggested an improvement over the hover model which is commonly known for the high-speed condition. Sartori and Yu [9] proposed a systematic method to identify parameters that can provide accurate thrust and drag prediction using Blade Element Theory (BET). As a theoretical basis, they used the Blade Element Theory (BET) as formulated by Leishman [10] coupled with the flapping model of Hoffman [5]. The unknown parameters were evaluated using data from static thrust setup and flight data. They concluded that the thrust estimation based on BET has difficulties in representing the trend of the experimental data for low rotor angular speeds. In particular, when the rotors were spinning under 6200 rpm the model considerably underestimates the thrust force. They proposed to use (BEMT) for the estimation of the rotor inflow since it provides a more accurate representation of flow variable along the blade span. The mathematical model for BEMT under different scenario has been discussed by Bangura et al. [11].

The measurement are very essential components for validating the models and also for providing suitable data for flight dynamic control. Storch et al. [12] developed a multi-thrust and multi-torque aerodynamic balance for measuring thrusts and torques of a pair of coaxial contra-rotating propellers. Various aspects, such as propeller distance and speed of rotation ratio were investigated by Storch et al. [12]. Molter and Cheng [13] designed and tested a multi-copter aircraft for measuring the wind speed near to the propellers.

Several opensource software have been used for estimating the hover performance of a multi-copter rotor in the absence of wind. Molter and Cheng [13] developed a computer program for estimating the propeller performance in forwarding flight. Holzsager [14] studied the effect of coaxial propellers for the propulsion of multirotor systems. Yilmaz and Hu [15] performed numerical analysis for the aerodynamics performance of two propeller designs at the static thrust condition. The first design is based on the original DJI Spark drone propeller blade and in the second design, a winglet was added to the first design. Leslie et al. [16] studied phenomena behind the source of noise produced by a propeller and according to authors a laminar separation bubble that occurs on propeller due to low Reynolds number conditions existing on blades is the major reason for this noise. According to authors the noise of the drone can be decreased by changing the shape, diameter, or angular velocity of the propeller. In their study, computational fluid dynamics (CFD) was an essential tool.

In the present study, a coupled CFD- BEMT approach for modelling single and counter-rotating propellers have been developed. The effect of propeller is modelled using Blade Element Momentum Theory (BEMT) and flow around the propeller is estimated using CFD. An experimental rig has been designed to estimate the thrust and torque of the propellers. The CFD-BEMT approach is validated with the available measurement data from open literature. The static thrust obtained from the CFD-BEMT has been compared with the experimental setup performed in the present study. Most of the previous studies are primarily focused on simplified modelling of the propellers. To the best of our knowledge, there are not many studies focussing on the CFD-BEMT approach. The approach does not require any hardware and therefore this approach can be referred to as virtual designing and testing of the propeller. The virtual setup can be utilized for estimating the dynamic loading of propellers.

2. Materials and Methods

2.1. Experimental Studies of Propellers

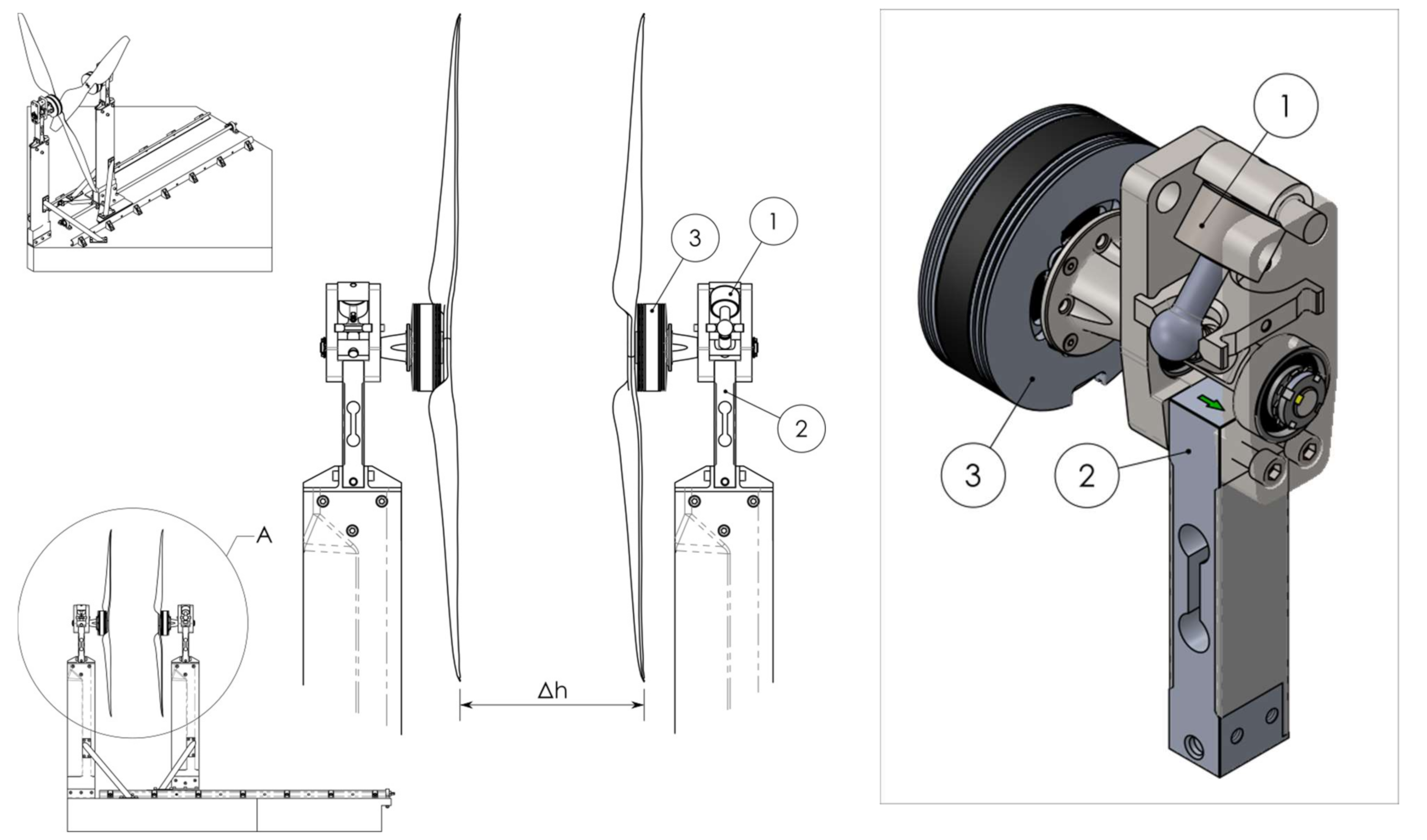
The test setup consists of a platform with two towers, one fixed and one movable allowing for adjusting the distance between propellers, see Figure 1. On top of the towers are placed measuring nacelles with integrated on them the thrust force (2) and torque (1) load cells. The test rig is meant for testing static (hover), as well as dynamic response of various propellers, motors, and speed controllers (ESCs). The rig consists of a heavy base and two aerodynamically shaped columns that can hold each of the two motors/propellers in a coaxial setup, or only a single motor/propeller in a single setup.

One of the columns is movable in the direction of the propeller rotation axis to enable adjustment of the distance between the two propellers in a coaxial configuration. Thrust force (2) and torque (1) are measured by respective load cells in the nacelles positioned at the top of each column. Nacelles were designed the way to allow the sensors for optimal measurement condition without off-axis forces or moments of force that could falsify the results. By measuring propeller torque, the rig is also able to measure the efficiency of the propeller(s) and the motor/ESC combo(s) separately. All sensors and actuators are interfaced with a custom data acquisition system (DAQ). In the setup control signal was fraction of throttle, 0.0–1.0 = 0%–100%. The data collection frequency in the current setup is 200 Hz. In the current setup following parameters can be measured individually for each propeller (1) thrust (axial load), (2) torque, (3) RPM (it is motor electrical RPM (ERPM) measured at the motor phase wire), (4) motor temperature, (5) current to ESC, (6) bus voltage (the bus voltage is the same for each ESC since they are on the same bus), (6) Power consumed [W], and (7) Power conversion (g/W). The whole system was calibrated with the following parameters:

• Thrust measurements are calibrated for offset, gain, and linearity in one direction with a 3rd-order polynomial using test weights; and
• Torque measurements are calibrated in both directions for offset, gain, and linearity using a torque arm and test weights.

The step static testing was conducted by a sequential increase of throttle from zero in a pre-defined number of steps to provide consistent data for each step. For temperature measurements to be valid, the duration of the static hover thrust test had been conducted from cold and limited to a few minutes to overcome the motor’s thermal time constant. The duration of each step was set to be 10 s with an increment of 10% of the throttle resulting in 11 steps in total. Data were considered stable when the noise level became stable and was determined by filtration of the signal. A 0% throttle was recorded in order to have noise level measurement for future reference. The propeller did not rotate at the first increment of the throttle, resulting in false readings from RPM and current (which gave unrealistic values of power consumption at close to zero RPM).

To remove the high noise/unreal/unstable section of the signal/singularities at low RPM, following filtration procedure steps:

• All RPM values bellow 100 RPM were dropped (no movement and noise level RPM signal) Result: only steps with following throttle levels were not dropped [0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1]
• The time to stable noise level differs between the steps. To standardize the number of readings, a single value, true for each step was selected. The last 1000 measurements of each step (last 5 s) of each step were used as stable.
• The remaining signal was used to calculate the average values of parameters for each step (Figure 2).

2.2. CFD-BEMT: A Numerical Approach for Modelling the Propeller

Qblade is open-source software that computes lift and drag coefficients of a given airfoil. Qblade is based on XFOIL (https://web.mit.edu/drela/Public/web/xfoil/). XFOIL is an interactive program for the design and analysis of subsonic isolated airfoils. It can be used in the viscous (or inviscid) analysis of an existing airfoil, airfoil design and redesign by interactive modification of surface speed distributions, and airfoil redesign by interactive modification of geometric parameters [17].

OpenFoam is an open-source computational fluid dynamic (CFD) (https://openfoam.org/) software used in solving flow related problems and in the present studies OpenFOAM has been applied for a flow analysis of the propellers. In CFD, the propeller can be modelled in two ways (1) direct method and (2) indirect method. In the direct method, the propeller geometry is resolved on the CFD grid allowing for the correct representation of the propeller surfaces. In the direct method, a 3D model of the propeller is imported in the CFD pre-processor and a mesh around the propeller is created. In this approach, more detailed features of the flow field around the propeller can be obtained. However, the direct method (resolving propeller on the grid scales) is computationally demanding and almost impossible to apply in the design and optimization of the propeller. The direct modelling approach requires many manual hours in establishing a propeller model needed for performing the simulations. To overcome this challenge and to speed up the simulation, another approach has been developed in which a mathematical model for representing the feature of the propeller has been developed and in this approach, the 3D model of the propeller is not required and therefore it does not require meshing of the propeller. This simplification leads to a computationally efficient solution [18]. This approach takes less time in establishing a simulation case enabling many simulations needed for finding the optimum size.

In the present approach, Navier–Stokes (NS) equation is solved on the grid to resolve the flow dynamics and the effect of propellers dynamics is introduced as a sink term in the momentum equation. Two fundamental conservation equations; conservation of mass and conservation of momentum have been solved.

The continuity equation or conservation of mass is:

$$\frac{\partial }{\partial t}\left(\rho \right)+\nabla ·\left(\rho \overline{u}\right)=0$$

(1)

The momentum equation is:

$$\frac{\partial }{\partial t}\left(\rho \overline{u}\right)+\nabla ·\left(\rho \overline{u}\otimes \overline{u}\right)=g+\nabla \left(\overline{\tau }\right)-\nabla ·\left(\rho R\right)+S_i$$

(2)

where $\rho$ is density of the medium, $\overline{u}$ is the velocity vector, $g$ is the gravitational force, $\overline{\tau }$ is the averaged stress tensor, and R the Reynolds stress tensor. The effect of the propeller on the flow is introduced via source terms $S_i$ to the governing equations for the cells in the mesh that are located inside a pre-defined propeller zone. These zones are predefined using OpenFOAM meshing option. As mentioned earlier, this approach is computationally cheaper than simulating an entire rotor blade geometry, but the resulting wake behind the propeller will only capture the time-averaged effects of the entire propeller on the flow field. Additionally, this approach cannot account for flow separation in the blades or other 3D effects such as shocks (for compressible cases), tip vortices, or hub horseshoe vortices. The source term in the momentum equation can be modelled either using the actuator disk (AD) or actuator line (AL) approach. The AD approach assumes a propeller rotor as a porous medium, and the AL approach resolves each blade of the propeller as a line or surface. In AL the propeller blades are represented by lines upon which distribution of forces acts as a function of local incoming flow and blade geometry. The main advantage of the actuator line model is the representing of the blades by its airfoil data that makes the approach well suited for wake studies. The rotational effect of blades, finite blade number effect, and the effect of non-uniform force distribution in the azimuthal direction are well incorporated in ALM.

In ALM, the propeller is modelled using Blade Element Momentum Theory (BEMT), this theory states that a propeller 3D geometry can be subdivided into multiple 2D sections along the length of the propeller. Then on each section, blade sectional forces thrust ($dT)$ and torque ($dQ)$ are calculated using the local flow velocity, flow angle ($\mathsf{\varphi })$, and blade section properties such as blade pitch angle$\left(\beta \right)$, chord (c), and tables of lift ($C_l)$ and drag ($C_d)$ coefficients around each section of the blade [19]. The following approach is used for estimating the source term that represents the propeller dynamics [18,20].

Step 1: Estimate the induction of the propeller using local flow velocity from CFD and use this induction factor to estimate the relative inflow angle. This is an iterative step.

$$\mathsf{\varphi }={\tan }^{-1}\left(\frac{1-a}{{\lambda }_r\left(1+a^{\prime }\right)}\right)$$

(3)

$$\frac{a}{\left(1-a\right)}=\frac{Bc(C_l\left(\alpha \right)\cos \left(\mathsf{\varphi }\right)+C_d\left(\alpha \right)\sin \left(\mathsf{\varphi }\right))}{8\pi r\sin {\left(\mathsf{\varphi }\right)}^2}$$

(4)

$$\frac{a^{\prime }}{\left(1+a^{\prime }\right)}=\frac{Bc(C_l\left(\alpha \right)\sin \left(\mathsf{\varphi }\right)-C_d\left(\alpha \right)\cos \left(\mathsf{\varphi }\right))}{4\pi r\sin \left(2\mathsf{\varphi }\right)}$$

(5)

Step 2: Estimate local angle of attack at airfoil section from relative inflow angle, pitch, and blade twist angle:

$$\alpha =\mathsf{\varphi }-\left(\theta +\beta \right)$$

(6)

Step 3: Estimate the lift and drag coefficient at various local angles of attack. The blade lift and drag coefficients for each section aerofoil are functions of the angle-of-attack and are interpolated from lookup tables:

$$C_l=\mathrm{f}\left(\alpha \right)$$

(7)

$$C_d=\mathrm{f}\left(\alpha \right)$$

(8)

Step 4: Estimate the blade sectional forces:

$$f_x=0$$

(9)

$$f_z=\frac{1}{2}\rho V^2\mathrm{c}\left(F{C}_{l}cos\mathsf{\varphi }-C_{d}sin\mathsf{\varphi }\right)$$

(10)

$$f_{\theta }=\frac{1}{2}\rho V^2\mathrm{c}\left(F{C}_{l}sin\mathsf{\varphi }+C_{d}cos\mathsf{\varphi }\right)$$

(11)

These forces $f\left(f_x, f_z, f_{\theta }\right)$ are estimated for the mesh points residing in the pre-defined propeller zone. The forces $f\left(f_x, f_z, f_{\theta }\right)$ are estimated in the rotor cylindrical coordinate system. For all the mesh points $\left(\mathrm{i}\right)$ residing in the pre-defined propeller zone, the forces $f\left(f_x, f_z, f_{\theta }\right)$ will be transferred from the rotor cylindrical coordinate system to the Cartesian coordinate system $F\left(F_x,F_y, F_{\theta }\right)$ using OpenFOAM inbuilt coordinate transform function:

$$F\left(i\right)={\mathrm{cylindrical}}_{-}>\mathrm{transform}\left(\mathrm{f}\left(\mathrm{i}\right)\right)$$

(12)

Step 5: The forces $F\left(i\right)$ are point forces and these forces will be converted into a volume forces using the following formulation [18].

$$Forc{e}_{cell}\left(i\right)=\frac{B}{2\pi }\frac{Are{a}_{cell}}{r_{cell}}F\left(i\right)$$

(13)

Step 6: Finally, the source terms needed in the momentum equation is implemented in the following manner:

$$S_i=\frac{F\left(i\right)}{V_{cell}}$$

(14)

with:

⚬

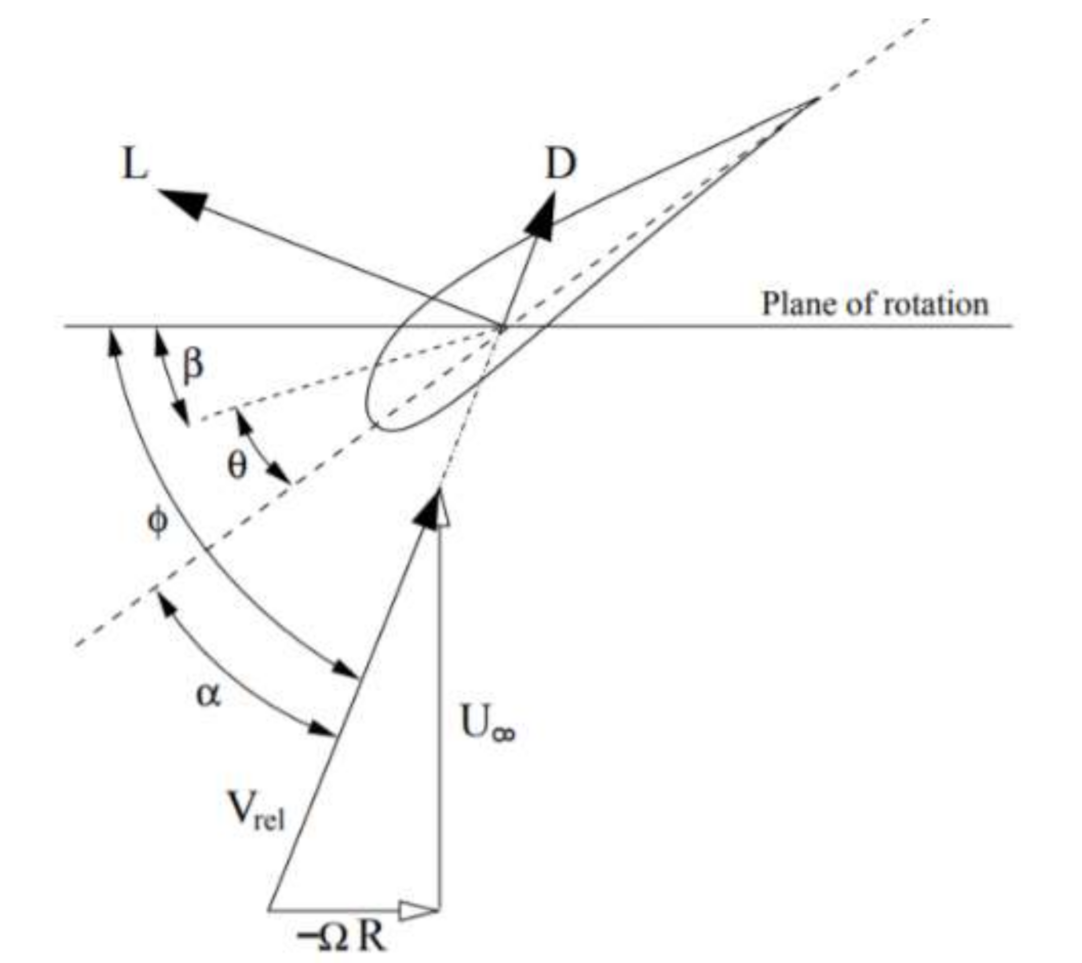
Φ (degree) the relative inflow angle (all the angles are defined in Figure 3)

⚬

λ (-) the speed ratio

⚬

α (degree) the angle of incidence

⚬

β (degree) the pitch angle

⚬

θ (degree) the twist angle

⚬

a (-) is the axial induction factor

⚬

a’ (-) the rotational induction factor

⚬

B (-)the number of blades

⚬

c (m) the chord

⚬

r (m) the radial position along the blade.

⚬

$r_{cell}$ (m) is the radial position of the mesh points residing in the pre-defined propeller zone

⚬

$Are{a}_{cell}$ (m²) is the area of the cells residing in the pre-defined propeller zone

The tip factor F accounts for the decreased lift in sections close to the blade tip due to the presence of a tip vortex which decreases the lift near the blade tip but does not significantly affect drag. In the present OpenFOAM model, the tip correction model suggested by Prandtl and improved upon by Drela [17] have been employed:

$$F=\frac{2}{\pi }\cos \left(\exp \left(-\sigma \right)\right)$$

(15)

$$\sigma =\frac{B}{2}\left(1-\frac{r}{R}\right)\left(\frac{R}{rtan\mathsf{\varphi }}\right)$$

(16)

This model by solving Equation (3) to Equation (16) has been implemented by Patrao [18] in OpenFOAM. In the present study, this model has been used for studying the propeller behavior.

Modelling of turbulence is very important and there are mainly three approaches for modelling the turbulence (1) Reynolds Averaged Navier–Stokes (RANS), (2) Large Eddy Simulation (LES), and (3) Direct Numerical Simulation (DNS). Both LES and DNS are computationally demanding and therefore these two approaches are not widely used in solving industrial flow related problems. RANS is a widely used approach for modelling the turbulent flow and in the current approach, the RANS approach has been used. However, a challenge with the RANS model is the selection of an appropriate turbulence model that is suitable for accurate estimation of the turbulent flow during the propeller motion. In the current study, the shear stress transport (SST) k-omega turbulence model is used. The SST model combines the k-omega and k-epsilon models. The k-omega model is more accurate near the wall and it is able to capture wall shear stress more accurately near to the walls, but these models are not well suited for free stream flows. On the other hand, the k-epsilon model gives better prediction in the freestream outside the boundary layer but the k-epsilon model fails to capture flow near to the wall. Hence a zone formulation was developed with a blending function to benefit from the best potential of both models [21]. In addition to continuity and momentum equations, a transport equation of turbulence kinetic energy and turbulence energy dissipation have been solved.

The governing equations of the model are the turbulence specific dissipation given by [22]:

$$\frac{D}{Dt}\left(\rho \omega \right)=\nabla ·\left(\rho D_{\omega }\nabla \omega \right)+\frac{\rho \gamma G}{\upsilon }-\frac{2}{3}\rho \gamma \omega \left(\nabla ·u\right)-\rho \beta {\omega }^2-\rho \left(F_1-1\right)C{D}_{k\omega }+S_{\omega },$$

(17)

and the turbulent kinetic energy is given by:

$$\frac{D}{Dt}\left(\rho k\right)=\nabla ·\left(\mathsf{\rho }{D}_k\nabla \mathrm{k}\right)+\rho G-\frac{2}{3}\rho k\left(\nabla ·\mathrm{u}\right)-\rho {\beta }^{\ast }\omega k+S_k$$

(18)

OpenFOAM solves Equations (1), (2), (17), and (18) simultaneously. The source term in Equation (1) is estimated by solving Steps 1–5.

2.3. Model Validation

The CFD-BEMT approach developed in the previous section has been validated with two APC propeller [23]. To test the validity of the CFD-BEMT approach, the experimental data of a real propeller: APC 10 × 7 and APC 11 × 7 Slow Flyer available in the UIUC propeller database site have been selected. The propeller information including geometry details of the APC can be found online on the website of APC [23]. The APC Slow Flyer is a two-bladed propeller, with a fixed pitch and a diameter. The propeller might be consisting of thin airfoil profiles with a specific combination of a low Reynolds number Eppler E63 and a Clark-Y airfoil near the tip, inserted to form a sharp leading edge blade design [23]. One of the challenges in the CFD-BEMT method is the accurate representation of the airfoil section of the blade. From the manufacture homepage, it is rather easy to find the propeller geometry in terms of chord and blade angle distribution but the airfoil shape of the propeller is proprietary of the manufacture and it is difficult to obtain the airfoil section details. 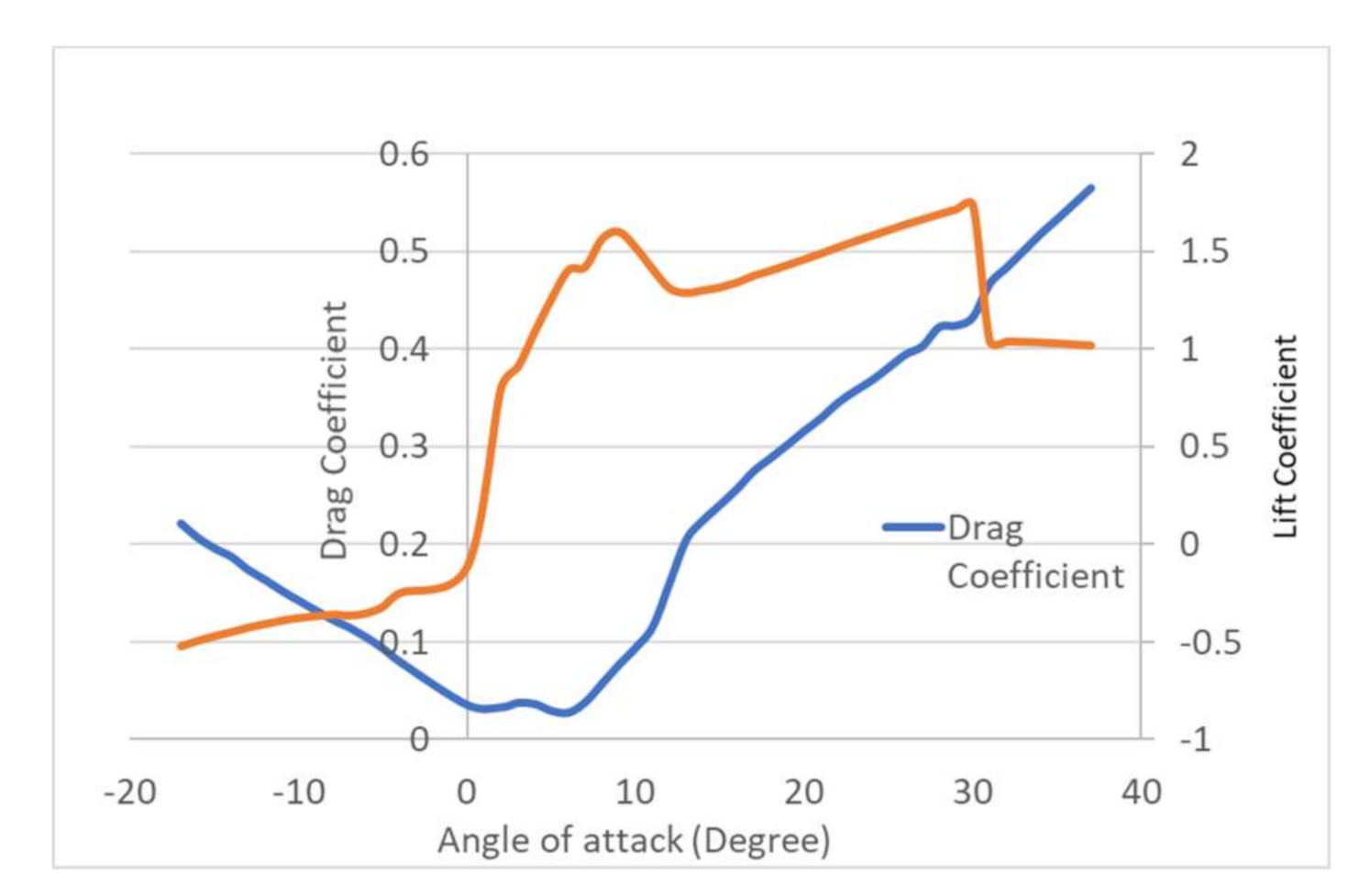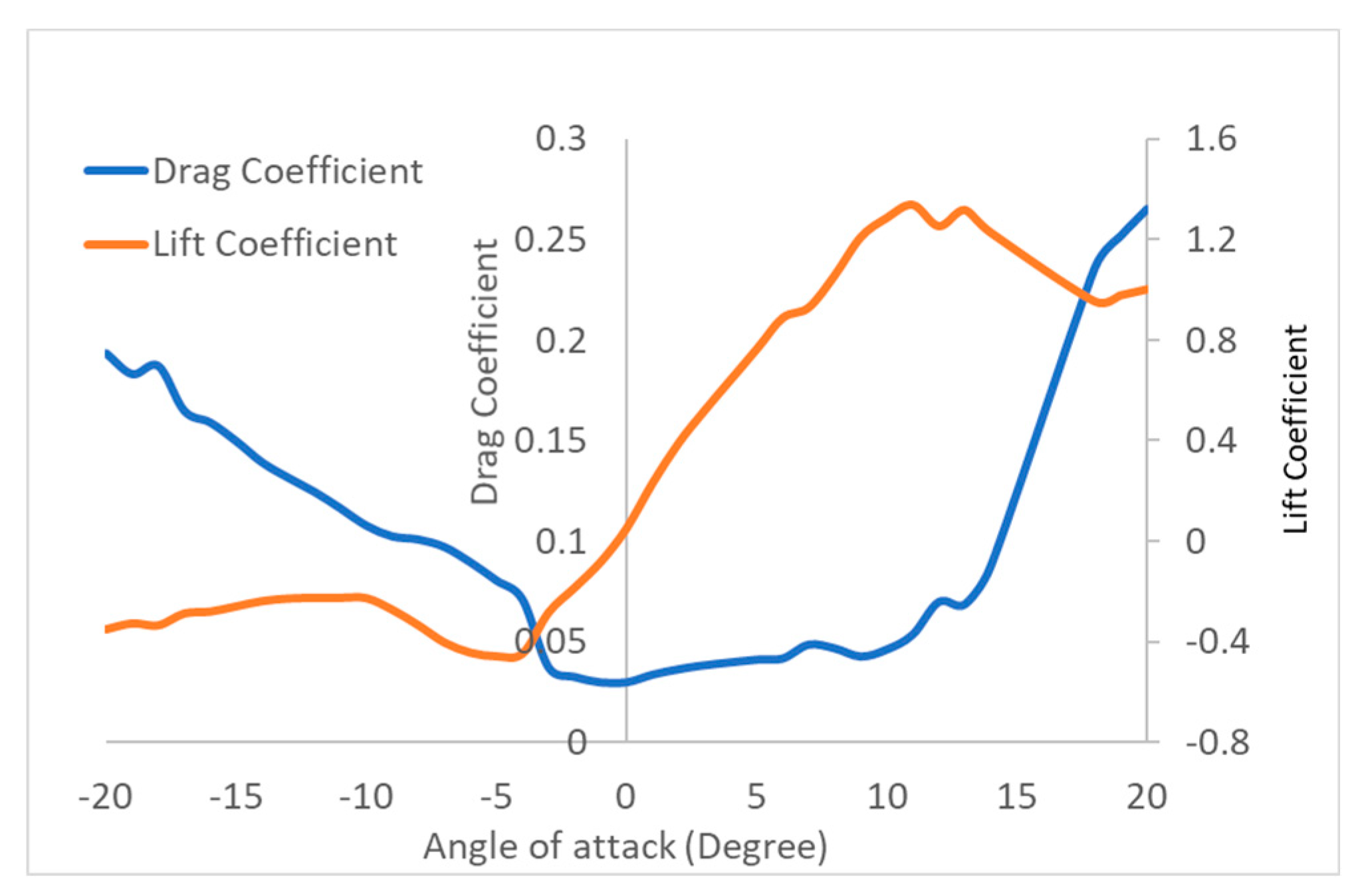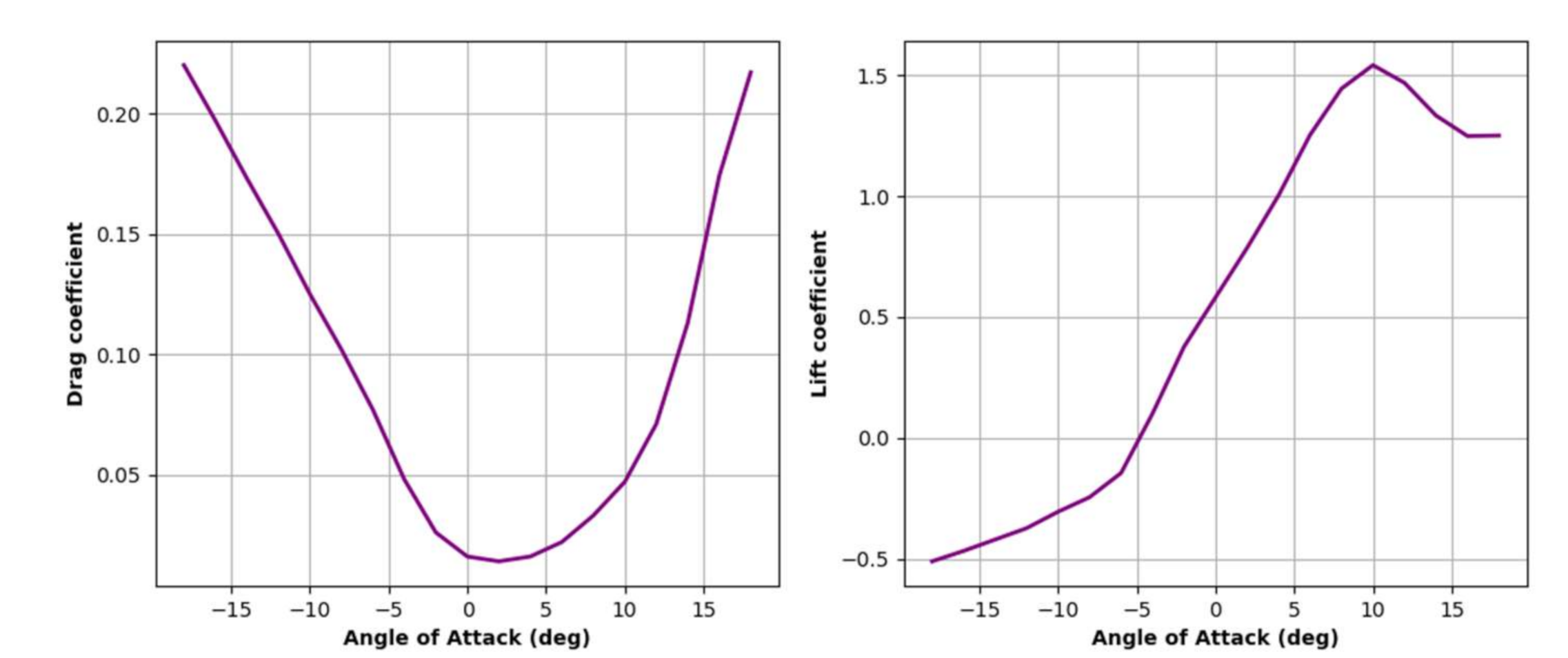However, It has been shown that using 3D scanning to capture the exact airfoil sections can lead to good agreement with experimental data [24,25]. However, in the absence of actual airfoil data, in the first attempt, it was assumed that APC SF propeller consists of Clark-Y airfoil. The lift and drag coefficients of the Clark-Y airfoil were estimated using Qblade. The parameters used in estimating the lift and drag coefficients are Reynolds number (Re) = 5 × 10⁴, and angle of attack range = [−20:20]. The lift and drag coefficients found with Qblade for the Clark Y airfoil are shown in Figure 4.

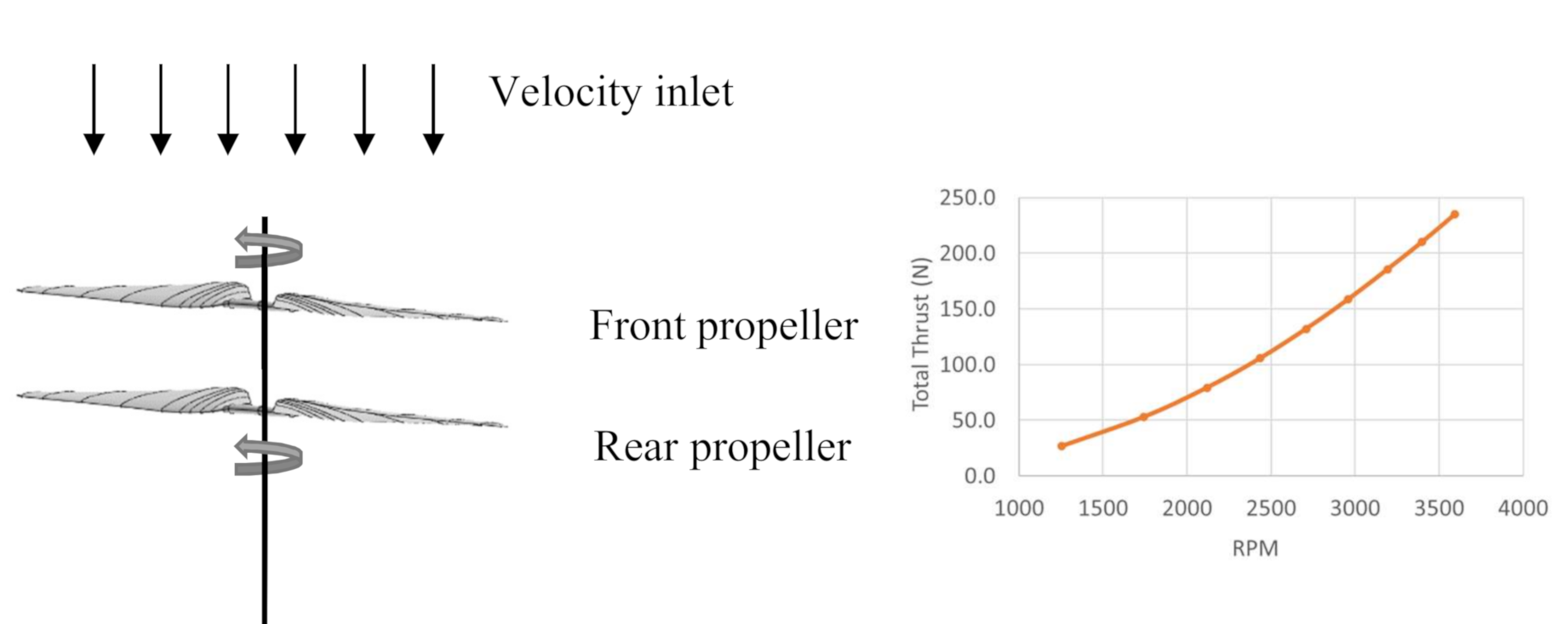
In OpenFOAM, the CFD-BEMT approach is implemented via fvOption and this can be used either using steady solvers such as simpleFoam or unsteady OpenFOAM solver such as pisoFoam. In the present study, only steady-state solver simpleFoam has been used. In CFD, the computational domain consisting of a mesh, boundary conditions, initial condition, etc., is an important step towards full simulations. A 3D computational domain used in the study of single and coaxial propeller is shown in Figure 5.

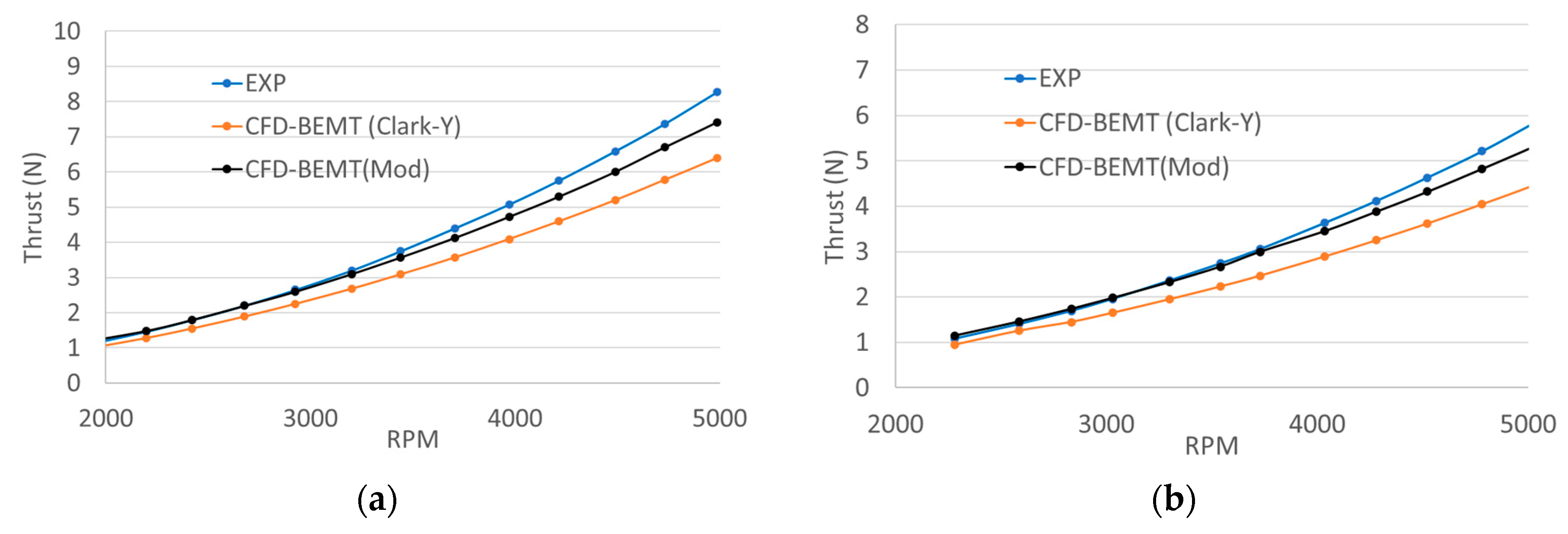
Mesh is generated by blockMesh in OpenFOAM. The mesh around the propeller was refined using appropriate stretching functions. On the left and right sides of the boundary pressure inlet-outlet boundary condition has been used to ensure that the flow can come either left side or right side depending on the propeller rotation direction (clockwise/counter-clockwise). This boundary condition ensures that the flow direction follows the propeller rotation. The other surfaces bottom, top, front and back surfaces are defined as free slip boundary conditions to avoid any disturbances. The Reynolds-averaged Navier–Stokes (RANS) equations in which the SST k-omega turbulence model was used to handle turbulence transport. OpenFOAM simpleFoam solver was used and the simulations were run until flow equations (mass, momentum, and turbulence) residuals were much lower than the prescribed values. The major input parameters needed to run the CFD-BEM approach are lift and drag coefficient of different sections of airfoils, a radius of the propeller, twist, and chord distribution of the blade along the length of the blade, and rotational speed of the propeller. 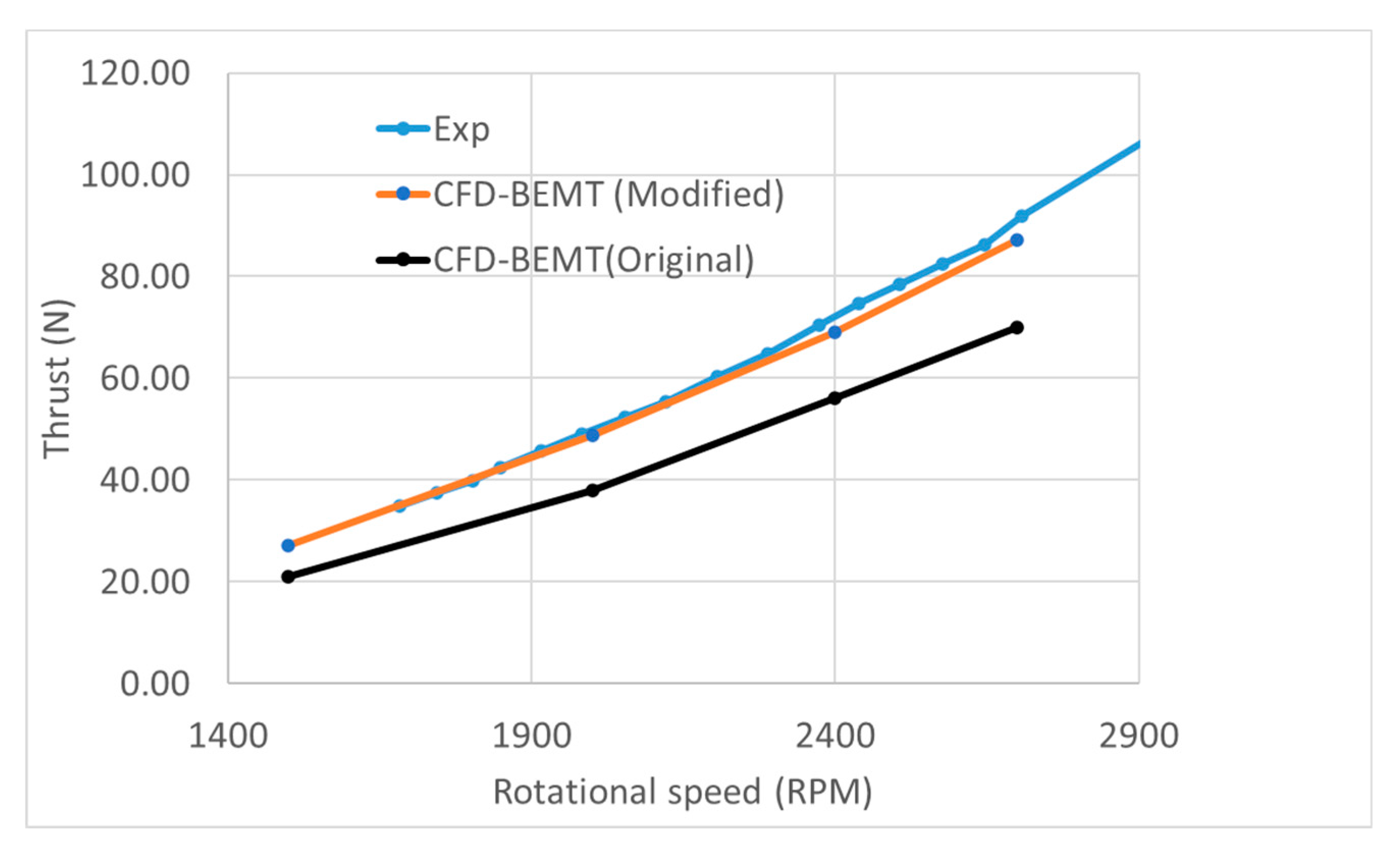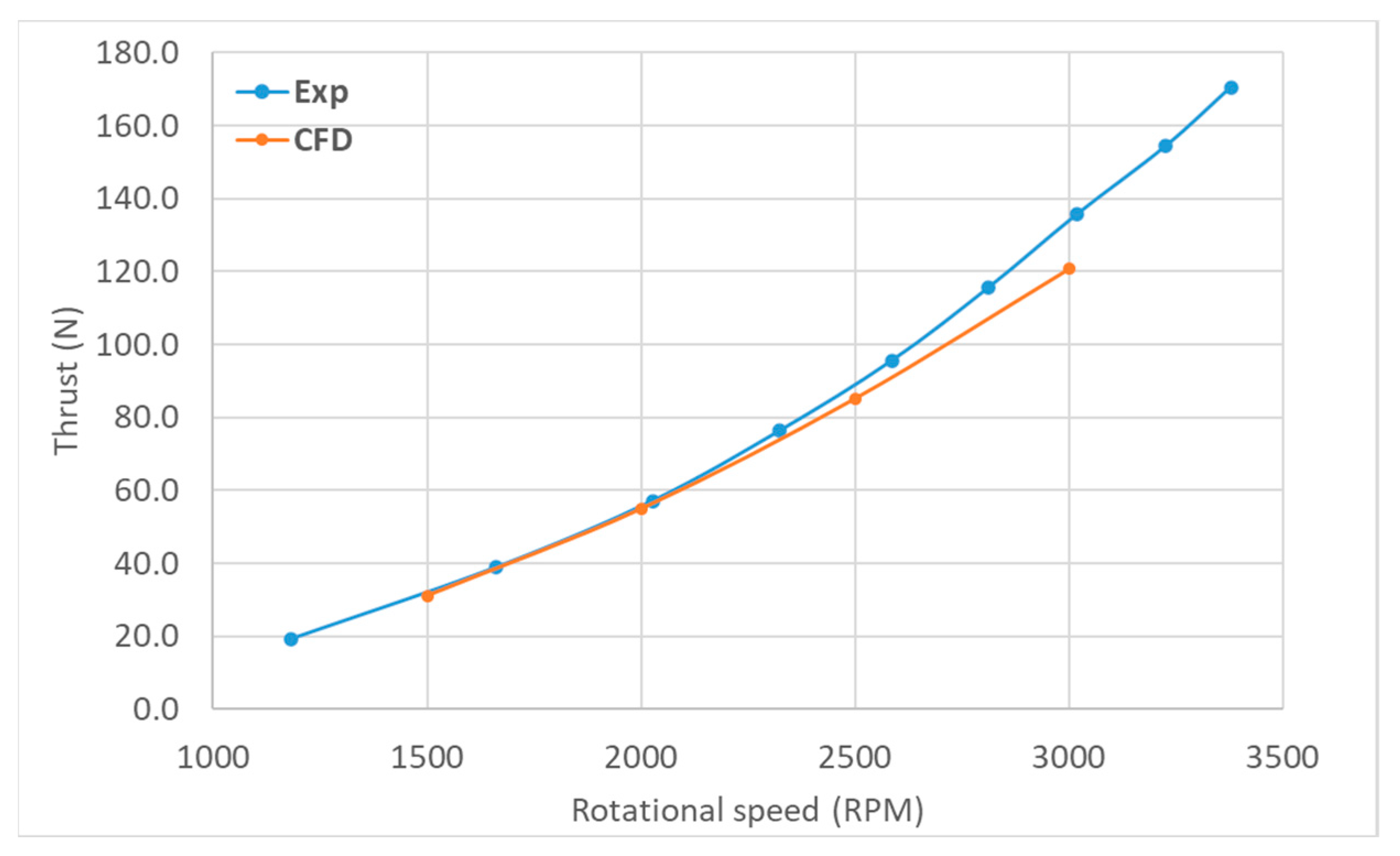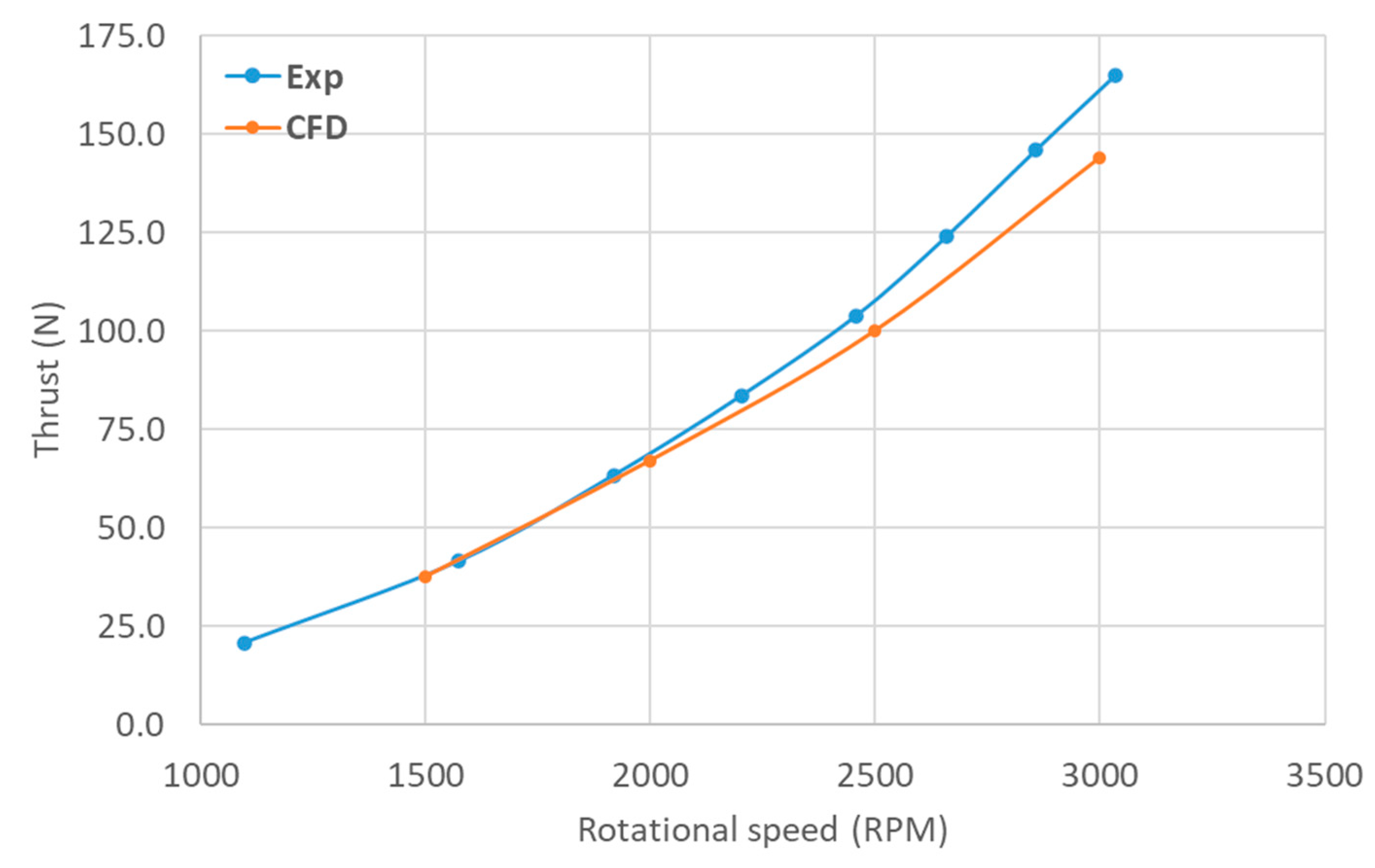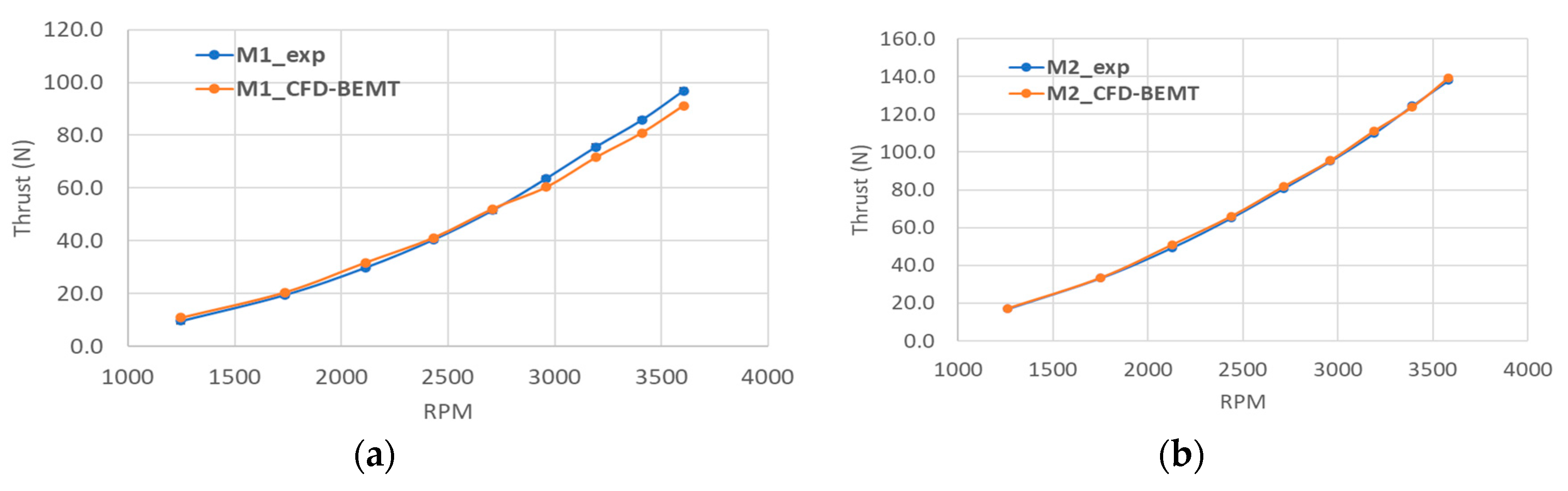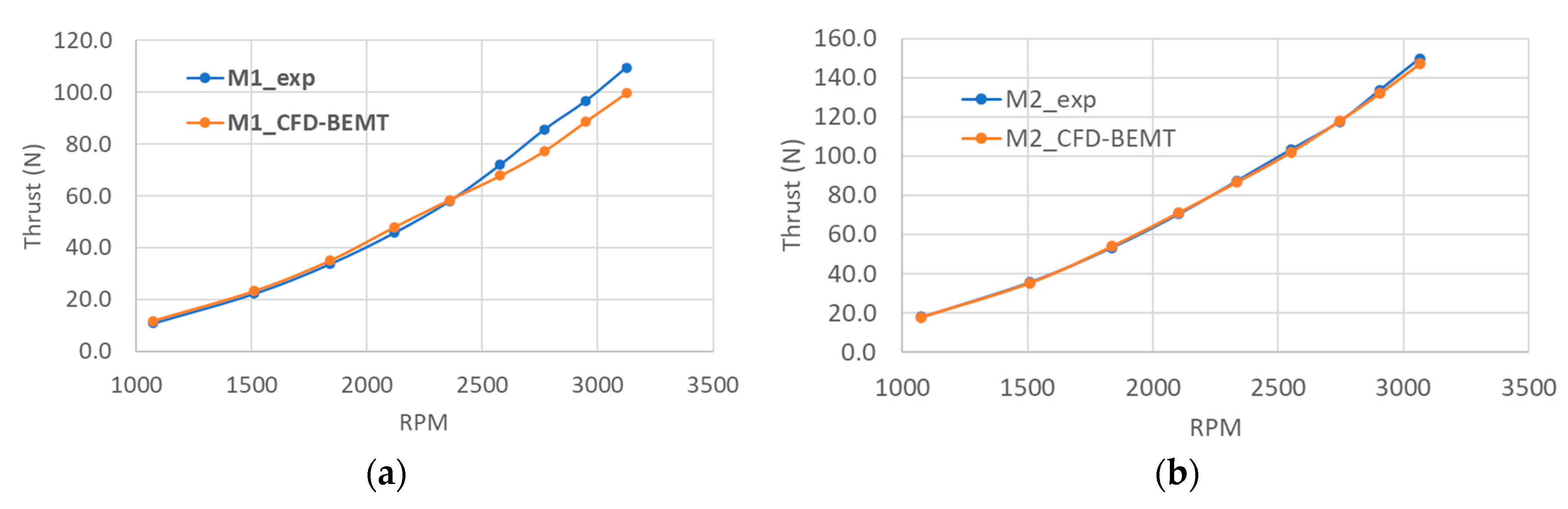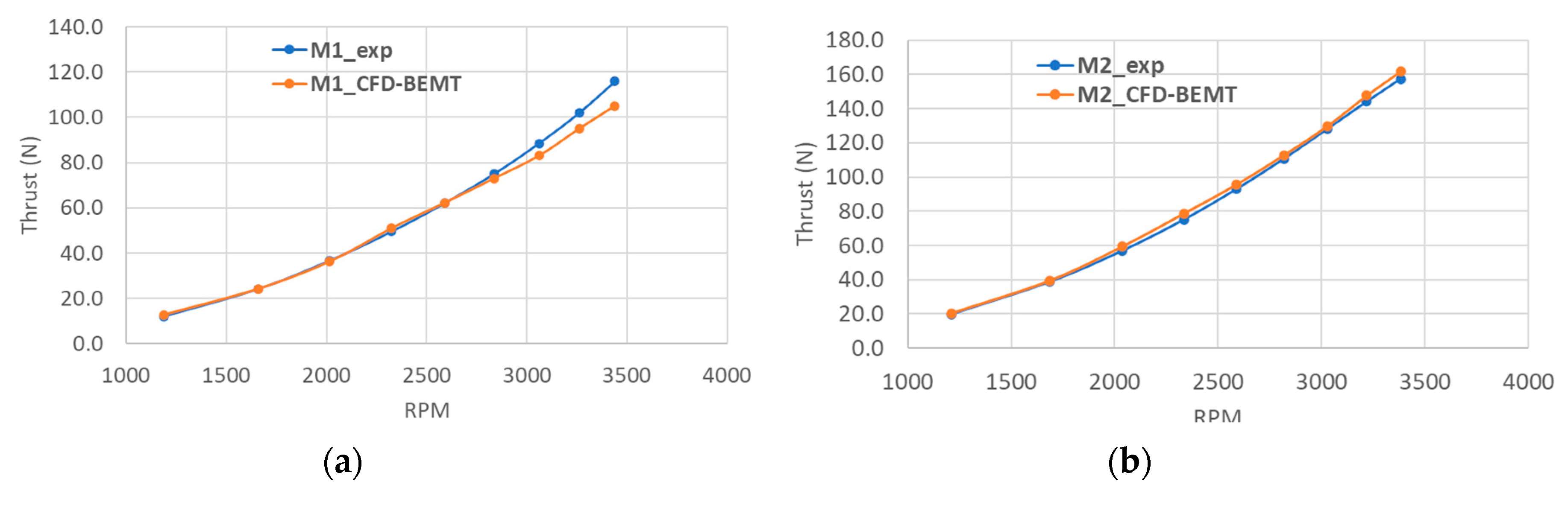The static thrust of APC 10 × 7 and APC 11 × 7 propellers for a Clark-Y airfoil at various rotational speed is shown in Figure 6a,b, respectively.

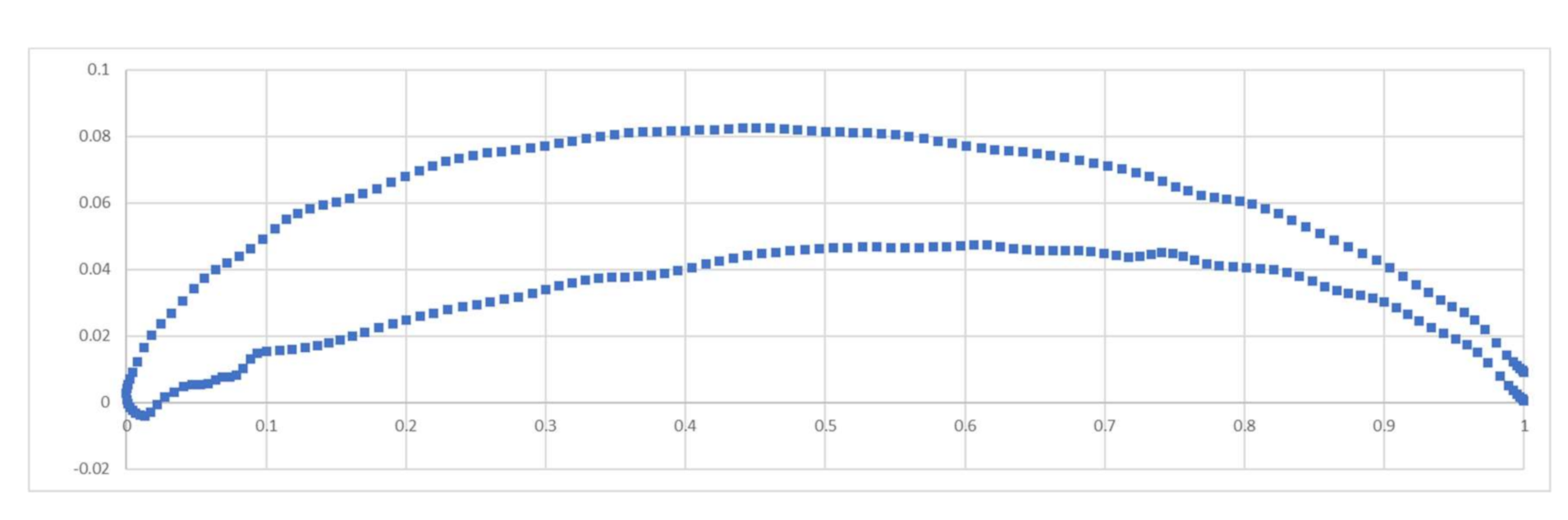
It can be seen from Figure 6a,b that the predicted static thrust of both the propeller with Clark-Y airfoil is underpredicted compared to the measured data. One of the reasons for this could be the lift and drag coefficients of the airfoil section used in CFD-BEMT simulation are not exactly similar to the one used in APC propeller. APC profiles are based on the modified Clark Y airfoil but in the CFD-BEMT simulations lift and drag coefficients of original Clark Y airfoils have been used. However, there is a significant effect of the lift and drag coefficient on the static and dynamic thrust of the propeller. The CFD-BEMT simulations of both the propeller (APC10x7 and APC11x7) at various rotational speeds were repeated with the airfoil shape nearly similar to the actual geometry. The airfoil section of the APC-SF propeller was scanned by Morgado [26] at a 75% radius of the propeller and the airfoil section is shown in Figure 7. He cut the blade with a vertical band saw machine in the 0.75R position along the blade’s chord. The lift and drag coefficient of the scanned airfoil geometry was used for estimating the lift and drag coefficients. The Reynolds number of the propeller is 50,000, which is defined by the rotational speed of 3000 RPM and a chord at a 75% blade station. Both lift and drag coefficients of the modified airfoil as shown in Figure 8 were estimated using QBlade at a Reynolds number of 50,000. In the present study effect of rotational speed on the Reynolds number was neglected. The lift and drag coefficient of the modified scanned airfoil is shown in Figure 8. The modified lift and drag coefficients were used for estimating the static thrust of both APC 10 × 7 and APC 11 × 7 propellers using the CFD-BEMT approach. The predicted static thrust with modified lift and drag coefficient for APC 10 × 7 and APC 11 × 7 airfoil is shown in Figure 6a,b respectively. The predicated thrust compares well with the measurement data at low rotational speed but at higher rotational speed the CFD-BEMT approach slightly underpredicts the thrust.

The reason for the underprediction could be, the current BEM does not include the effects of ‘3D correction’ due to the rotation of the wind turbine blade and effect of rotational speed on the Reynold number. The ‘3D correction’ accounts for the lift augmentation caused by rotation and these effects dominates at higher rotational speeds. Many studies have shown that the rotation of the blade significantly affects the aerodynamic coefficients of airfoil sections, in particular around stall [27,28,29]. Besides, the lack of aerodynamic data for both high angles of attack and varying Reynolds number leads to difficulty in accurately modelling the propeller performance at higher rotational speeds. In the present study, these corrections have not been included and will be studied in future work [29].

2.4. The Static Thrust of Reference Propeller

Propellers have constantly faced design challenges to improve efficiencies and operational usages. If quadcopters are to be used, then maximizing their operational efficiency is critical and aerodynamic behavior is very crucial and these propellers have to be designed to meet the specific requirements. Drone propellers need to be designed to generate enough thrust to carry the take-off weight and maintain a good lift to drag ratio. The propeller design parameters include blade number, diameter, section geometry, pitch angle, and twist angle. Studies of a single propeller and coaxial propeller have been performed to estimate the static thrust of the propeller. However, it will be a challenge for many drone developers to design and develop a new propeller to suits their requirements and a common practice is to purchase available propeller with a known diameter and pitch angle. However, these propellers do not include any information regarding the airfoil profile of the propeller blades. A common practice adopted by a drone developer is to purchase a propeller and perform some experimental studies to meet the specified requirements. The drone developer performs static thrust experiments on the propellers to identify the optimum propeller. These tests are time-consuming delaying the overall product development time. To enable faster evaluation of different drone propeller a modeling approach described in the previous section has been applied to the three propellers which have been identified by Sevendof AS for their drone.

Three propellers have been studied: SevenDOF3232 (32 × 11), SevenDOF3234 (34 × 11.5), and SevenDOF3236 (36 × 11.5). The actual names of the SevenDOF32 propellers are not disclosed due to a confidential issue.

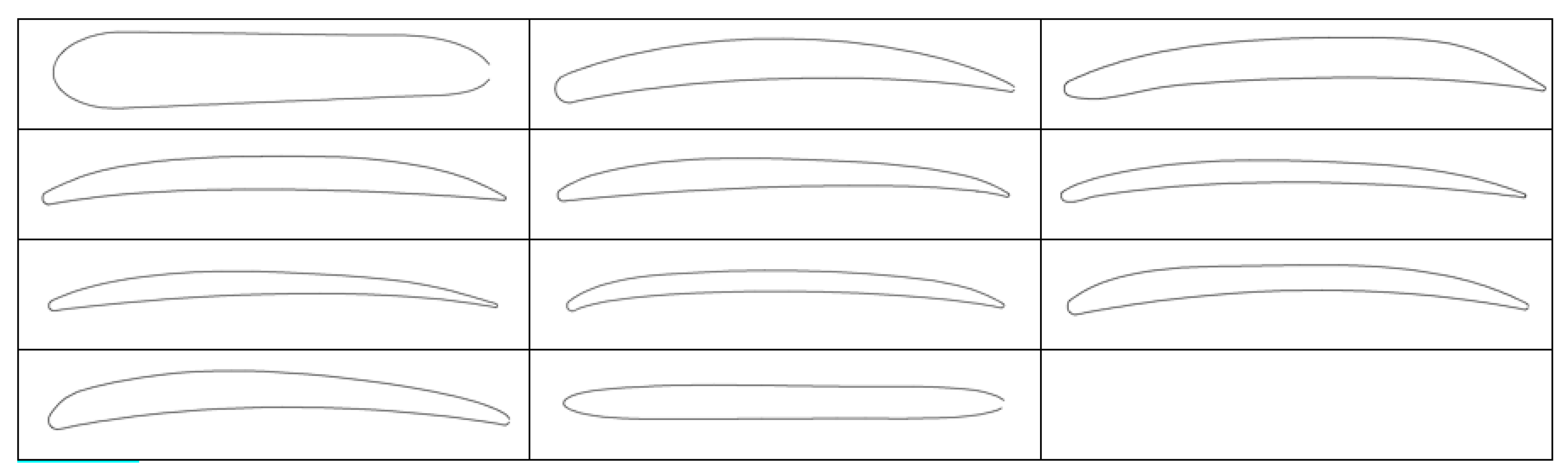
The coordinate of various sections of the SevenDOF3232 propeller have been extracted using scanning techniques and these sections are plotted in Figure 9. The geometry of propeller was retraced by using an Occipital Structure Sensor (Mark I) 3D scanner with ±0.1 mm accuracy. The point cloud was used to recreate the airfoil profile in CAD software with the use of direct measurements with an accuracy of ±0.01 mm. However, the scanning technique is time-consuming and cannot be applied for scanning all the SevenDOF32 propeller. Therefore, the airfoils sections of SevenDOF3232 will also be used for the SevenDOF3234 and SevenDOF3236 as an approximation to the real geometry. The modelling of the propeller requires aerodynamic data of the different sections. A description of the aerodynamic data has been provided in the result and discussion section.

3. Results and Discussion

3.1. Single Propeller Setup

The geometry of several airfoils sections along the propeller length is shown in Figure 9. The propeller blade was scanned along the chord of the blade and airfoil distribution is shown in the figure.

The aerodynamics coefficients of these airfoil sections were computed and the average value of lift and drag coefficient of the propeller is presented in Figure 10. However, the estimated aerodynamics coefficients might not be that accurate because the airfoil’s geometric shape of the propeller is not accurate enough. This could be due to the post-processing and scanning of the propeller geometry. Furthermore, the conversion from 3D scanned data to a digital format is not always accurate. Additionally, the blade geometry was also scanned to obtain the blade angle and chord distribution along the length of the blade. The other uncertainties as described earlier, the present CFD-BEMT approach does not include the effects of blade rotation on the aerodynamic coefficients and also it does not account for the effect of propeller rotation on the Reynolds number. To compensate for the uncertainties associated with the airfoil digitalization, Reynolds number corrections, and 3D rotational effects at higher speeds, both the lift and drag coefficient were adjusted by a multiplication factor. The cfd-bemt simulation of the SevenDOF3232 propeller was performed and the static thrust of the propeller as a function of rotational speed is shown in Figure 11 In the present study, the multiplication factor was around 1.7. the estimated results with and without multiplication factors are compared with the measurement data and the comparison is shown in Figure 12 and the estimated values with and without the multiplication factor were deviated by 20% and less than 5% at higher rotational speeds.

The SevenDOF3234 propeller had a diameter of 34 inches and a pitch of 11 inches and SevenDOF3236 propeller had a diameter of 36 inches and a pitch of 11 inches. It was very challenging to scan the propeller of SevenDOF3234 and SevenDOF3236 to obtain the geometrical details of the blade and also the airfoil profiles of the propeller section. In the present study, for SevenDOF3234 and SevenDOF3236 propeller, the lift and drag coefficients of SevenDOF3232 propeller with a multiplication factor of 2.2 were used to account for uncertainties in the geometry and modelling. The lift and drag coefficients as shown in Figure 10 were used in calculating the static thrust of the propeller. Again CFD-BEMT simulations of both propeller were performed with the multiplication factor and a comparison between predicted and measured data of SevenDOF3234 and SevenDOF3236 are shown in Figure 12 and Figure 13, respectively.

3.2. Coaxial Propellers Setup

The coaxial rotating propeller, comprising two coaxial propellers sited one behind the other and rotating in opposite directions, has traditionally been used in many aerodynamic applications. Contra-rotating co-axial propulsion systems have the aerodynamic advantage of recovering part of the slipstream rotational energy which would otherwise be lost to a conventional single rotating propeller. Furthermore, because of the two-propeller configuration, contra-rotating propellers possess a capability for balancing the torque reaction from the propulsor which is an important matter for the overall balance of the system. Co-axial propeller systems have been used successfully in fixed-wing aircraft for many years due to their inherently good performance. A study carried out by Prior [30] showed that although the co-axial arrangement has a reduced power output of up to 15% when compared to an equivalent single rotor system, this can be offset by the elimination of the need for a tail rotor, which could save up to 20% of the required power.

A schematic of the set-up can be found in Figure 14 in which two-propellers are shown at a certain distance. Both the propeller front and back are exactly similar and the gap between the propeller can be varied but for the current numerical simulation, a gap of 160 mm is selected due to the mechanical and mass requirements of the drone in development. The aim of using coaxial propellers is to increase the thrust without increasing the footprint of the vehicle. As mentioned, the current approach does not require the geometrical features of the propeller which simplifies setting up the co-axial simulations in the CFD framework. The virtual model approach is used where only propeller lift and drag coefficients of different sections of the propeller are used. The lift and drag coefficients of a single SevenDOF3232, SevenDOF3234, and SevenDOF3236 propeller as described in the previous sections were used in the coaxial studies. A CFD model of the coaxial propeller was prepared and both experimental and numerical studies of the coaxial propeller were performed. For experimental studies, the setup explained in the previous section have been employed. Both the propellers were attached to separate power supply and the distance between these propellers can be changed (see Figure 1). The thrust profile as a function of the rotor speed of the coaxial SevenDOF3232 propeller is shown in Figure 14.

The simulation studies of three counter-rotating (CR) CR-SevenDOF3232, CR-SevenDOF3234, and CR-SevenDOF3236 propellers were carried out using CFD-BEMT. The mesh used in these simulations was similar to the one shown in Figure 5. Except the length of the computational was larger than the single propeller simulation case. The multiplication factor of 1.8, 2.2, and 2.2 for CR-SevenDOF3232, CR-SevenDOF3234, and CR-SevenDOF3236 propellers were used, respectively. Again these multiplication factors were used to account for uncertainties in both geometry and CFD-BEMT modeling.

The thrust forces of front and back propeller of CR-SevenDOF3232, CR-SevenDOF3234, and CR-SevenDOF3236 from CFD and experiments are shown in Figure 15, Figure 16 and Figure 17 respectively. The thrust forces of the front propeller from CFD compared well with the measured thrust value for all the co-axial configuration at all the rotational speeds. However, the thrust of the rear propeller is under predicated at higher rotational speeds for all the co-axial configuration and that is because the rear propeller is in the wake of the front propeller and wake recovery estimated with CFD is slower compared to the real scenario. This could be due to the choice of turbulence model and chosen turbulence parameters. Nevertheless, the difference between computed static and the measured thrust is within 5–10%.

4. Conclusions

An experimental approach of estimating the single and coaxial propeller thrust and torques as a function of rotational speed has been presented. These experimental setups were designed to characterize different kinds of propellers available commercially. A dynamic coaxial propeller setup was designed to identify the optimal distance between two counter-rotating propellers. To avoid the cost and time needed for performing the experiments, a numerical model of the single and coaxial propeller has been developed in the CFD-BEMT framework. The main input parameters for estimating the static or dynamic thrust are the geometrical details of the propeller blade such as blade angle and chord distribution along the length of the blade. In addition to this, the lift and drag coefficients of the propeller airfoil are used. The numerical models have been calibrated and validated with the experimental data. This study shows that by multiplying aerodynamics factors to compensate for unknown parameters, a model mimicking the behavior as close to the real model can be obtained. The CFD-BEMT approach can be used in assessing the propeller performance in both static and dynamic conditions provided the aerodynamic coefficients of the propeller are accurate enough. The uncertainties such as three-dimensional lift and drag effects and effect of rotation on the Reynolds number will be studied in future studies.