Computationally Efficient Force and Moment Models for Propellers in UAV Forward Flight Applications

Abstract

Two low-order, parametric models are developed for the forces and moments that a rotating propeller undergoes in forward flight. The models are derived using a first-principles-based approach, and are computationally efficient in the sense of being represented by explicit expressions. The parameters for the models can be identified either using supervised learning/grey-box fitting from labelled data, or can be predicted using only the static load coefficients (i.e., the hover thrust and torque coefficients). The second model is a multinomial model that is derived by means of a Taylor series expansion of the first model, and can be viewed as a lower-order lumped parameter model. The models and parameter generation methods are experimentally tested against 19 propellers tested in a wind tunnel under oblique flow conditions, for which the data is made available. The models are tested against 181 additional propellers from existing datasets.

1. Introduction

Aerodynamic models of a rotating propeller in forward flight can be broadly classified into two categories. The first category is high fidelity models that may involve a fluid dynamics simulation and uses relatively high compute power to resolve. These models are typically used to aid the design of the propeller and/or vehicle [1,2,3]. The other category, which is the focus herein, are low-order yet computationally efficient models that can make use of experimental data for grey-box identification. There is a lack of literature on the latter category, as noted in [4,5,6,7], especially for vertical take-off and landing (VTOL) unmanned aerial vehicles (UAVs) due to the wide operating regime spanning hover, axial, and oblique flows. Such models would be useful for model-based control and state estimation [8,9,10], where only the salient features need to be captured, and can improve the fidelity of simulations of UAV control systems.

Specifically, the goal herein is to derive parametric models via first-principles for the propeller thrust $F_T$, “H-force” (sometimes referred to as rotor drag) [11,12] $F_H$, rotor torque $M_Q$, rolling moment $M_R$, and pitching moment $M_P$ (see Figure 1; the lateral/side force $F_S$ is two orders of magnitude smaller than the thrust, as can be seen in Supplementary Dataset S1, and thus is assumed to be negligible), given a propeller’s rotation rate $\mathsf{\Omega }$, incoming wind speed V and angle between the rotor plane and incoming wind $\beta$, to a reasonable degree of accuracy. That is,

$$\begin{array}{c}\hfill (\mathsf{\Omega },V,\beta )\mapsto (F_T,F_H,M_Q,M_R,M_P)\end{array}$$

(1)

where the above map is given as an explicit expression of its arguments $\mathsf{\Omega },V$ and $\beta$. That is, no implicit equations, no numerical computation of integrals, etc. This is a useful attribute because explicit expressions are simple and typically fast to compute and have low memory footprint. The benefit of such grey-box models is that they are good at extrapolating measurement data (compared to a black-box approach). For instance, as will be shown in Section 4.2, the parameters to the model can be learned only from the hover thrust and torque coefficients, resulting in good extrapolation of the loads in the forward flight operating regime.

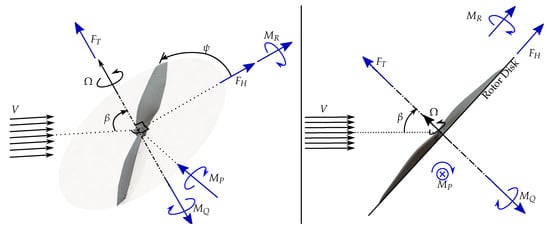
Figure 1. A counter-clockwise propeller rotating at a rate of $\mathsf{\Omega }$, with incident wind with speed V forming an angle $\beta$ with the rotor plane normal. $\psi$ is the azimuth angle of the propeller blade. The left figure is a 3D view and the figure on the right is a 2D side view. Note that the direction of the incoming flow is perpendicular to the direction of pitching moment $M_P$, which is perpendicular to the direction of H-force $F_H$ (and rolling moment $M_R$), which is perpendicular to the direction of thrust $F_T$ (and rotor torque $M_Q$). The forces act at the centre of the rotor disk. For a clockwise propeller, the directions of assumed positive rotor torque and rolling moment are flipped. The lateral or side force $F_S$ (in the direction of the pitching axis), is assumed to be negligible and is indeed the case in experiments, see Supplementary Dataset S1 and Figure 6.

This paper is organized as follows:

• Section 2 and Section 3: a first-principles-based analytical model is derived for (1). This model is parametrized by nine parameters, which can either be optimized over using labelled data generated from flight experiments as in [13,14,15], or against wind tunnel data as will be done herein. In contrast to the literature, this section provides a consolidated and analytical grey-box model for (1) without limiting restrictions on $\beta$. To the best of the authors’ knowledge, such a model does not exist in the literature. Additionally, wind tunnel tests were performed, generating a dataset consisting of 19 propellers under oblique flow ($\beta \not\equiv 0$), for which the models will be tested against. This dataset can be found in Supplementary Dataset S1. The models will be additionally tested against existing datasets which are predominately for axial flow ($\beta \equiv 0$).
• Section 4: an algorithm for which the nine parameters can be predicted using only the static thrust and torque coefficients (i.e., the hover model). Again, this approach is assessed with the full wind tunnel dataset. To the best of the authors’ knowledge, such an approach has not been explored in the literature.
• Section 5: a second-order Taylor series expansion is performed to yield a simplified lumped-parameter model. The contribution of this section over a brute-force, black-box multinomial surface fitting approach is that, based on the first-principles model, some terms disappear in the Taylor expansion, resulting in a reduced multinomial that is physically motivated. Again, this has not been done in the literature to the best of the authors’ knowledge, and the approach is assessed with the wind tunnel data.

The assessment against the wind tunnel data for each section not only assesses the quality of the models, but also provides a typical range of values for the parameters.

Literature Review

In the context of control of multirotor vehicles, the typical modelling approach has been to use a hover or ‘static’ model, that is, the thrust and rotor torque are proportional to the square of the propeller rotation rate, and to neglect H-force, pitching and rolling moments [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]. As shown in [15], this model breaks down when a quadrotor flies at moderate speeds. Thus in such cases, feedback control is relied upon to achieve adequate tracking.

In [9,10], model-based state estimation was improved upon by incorporating some of the forward flight effects of the propeller, namely the H-force $F_H$ (though this model still differs to the H-force models proposed herein). Furthermore, when considering the reduction in thrust $F_T$ in forward flight, one approach is to use momentum theory and Glauert’s flow model for helicopter rotors to yield an implicit equation for the induced flow that must be solved numerically [11,34,35,36,37]. This has been used in [38,39] to develop a thrust model as a function of the ideal power consumption of the rotor. This has also been used in [12] to model the thrust, H-force, and rotor torque for a helicopter rotor. In [35], building on [36], some simplifying assumptions are used in the context of helicopter rotors (e.g., $\beta \approx \pi /2$) to derive an analytical model for the thrust. A similar modelling assumption is used in [40], yielding a model (with $M_P$ neglected) that was used in [41] for improving the simulation of a quadrotor. In addition, a wind estimation algorithm using a quadrotor was developed in [42], where the rotor thrust was modelled using a black-box model using wind tunnel data.

In the context of fixed-wing aircraft control, some works forego the modelling task and elect to rely solely on feedback for thrust tracking, which has been shown to work for nominal cruise conditions [43,44,45,46,47]. Others also use the hover model mentioned earlier [48,49,50]. In [51,52,53,54], a black-box modelling approach is performed by using data from flight experiments and assuming a linear system about a specific operating point in order to achieve better closed-loop control performance.

Other fixed-wing works, such as [55,56], use a black-box modelling approach given wind tunnel data for the thrust $F_T$ and under axial flow conditions. In particular, it is stated in [55] that no physical explanation can be provided for their thrust model. In [57], a look-up table is used based on thrust values provided by the propeller’s manufacturer for various flight speeds under axial flow. Similarly, a look-up table approach is used in [58] to enhance the fidelity of flight simulations, where the values are generated under axial conditions for the thrust $F_T$ and torque $M_Q$ using computational software. In [59,60], a model for $F_T$ is used that takes into account some of the forward flight effects under axial flow conditions. In [61], attitude control was improved upon by incorporating the forward flight effects of the propeller using a grey-box model, but the modelling was done for a fixed angle of attack.

Recently, a few works have used blade element theory (BET) [5,6,14,15,62,63,64,65,66], usually in conjunction with the Glauert flow model [34] for both axial and oblique flow conditions, resulting in models with no closed form expressions. Additionally, the models are fragmented in the literature, with some focusing only on the axial flow condition, and others only considering a subset of the outputs in (1). In [13], a combination of first-principles and black-box modelling using stepwise regression was used given flight performance data. This is similar to our previous work [15], but the models were quite computationally expensive in the sense that they were not representable by analytical expressions, and thus must be solved numerically.

Performance data was gathered from wind tunnel experiments for a UAV and an isolated propeller in [67], and it was noted that there is a lack of published data for the aerodynamic performance for UAVs in general. In [58,68,69], a thorough wind tunnel data collection was performed for axial flow, resulting in a database for 180 different propellers. An additional wind tunnel measurement campaign was performed in [7] for both axial and oblique flow for a single propeller. All the models proposed herein will be assessed against these datasets, as well as against 19 additional propellers that were tested in a wind tunnel under oblique flow conditions (see Supplementary Dataset S1).

2. First-Principles Derivation

The overall derivation involves a blade element approach, where the propeller blade is divided into infinitesimal segments. A quasi-steady flow assumption is used, in the sense that the fluid equilibrates at a negligible time constant with respect to the time period of the propeller rotation. Furthermore, each blade segment is assumed to be independent of other segments in the sense that the flow around each segment can be viewed as being purely two-dimensional. This approach will be combined with momentum theory in Section 2.6 to resolve further variables in the model, namely the induced inflow. For convention, the direction of positive forces and moments are fixed and shown in Figure 1. Only the forward flight scenario is considered, that is $V\ge 0$, $\beta \in [-\pi /2,\pi /2]$, and $\mathsf{\Omega }>0$.

Consider now an infinitesimal blade segment at a distance $y\in [0,R]$ from the centre of the propeller, and let the segment have a width of $\mathrm{d}y$ (see Figure 2). Then, the components of the air velocity $U_{\Vert },U_{\perp }$, as defined in Figure 2, with respect to the moving blade segment are given by

$$\begin{array}{cc}\hfill U_{\Vert }(\mathsf{\Omega },V,\beta ,y,\psi )& =\mathsf{\Omega }y+Vsin(\beta )sin(\psi )\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill U_{\perp }(V,\beta ,v_i)& =Vcos(\beta )+v_i\hfill \end{array}$$

(3)

where $v_i$ is the induced inflow velocity through the rotor disk and is in a direction perpendicular to the rotor disk [34], and in the tangential direction is assumed to be negligible (see Section 2.6). It is assumed that the induced inflow is uniformly distributed across the rotor disk. The flow angle $\varphi$ in Figure 2 is given by

$$\begin{array}{c}\hfill \varphi (\mathsf{\Omega },V,\beta ,y,\psi ,v_i)=arctan2\left(U_{\perp }(\mathsf{\Omega },V,\beta ,y,\psi ),U_{\Vert }(V,\beta ,v_i)\right)\end{array}$$

(4)

Figure 2. An infinitesimal blade element (right) located at a distance y from the rotor centre with width $\mathrm{d}y$. $\alpha$ is the angle of attack of the blade element, c is its chord length, and $\theta$ is the pitch angle, the angle of the blade element’s chord line [70] with respect to the rotor disk. The infinitesimal loads of the blade element are the lift $\mathrm{d}L$, drag $\mathrm{d}D$, and pitching moment $\mathrm{d}M$.

The effects of blade flapping [10] have been ignored in the above. Simple models is one of the goals herein, and assuming that the UAV propellers are rigid enough to mitigate flapping effects will prove to be a good enough assumption as the models behave well in experiments. However, extending the derivation to include blade flapping effects to improve the models, especially for soft propellers, may be an interesting direction for future work.

Henceforth it will be convenient to work in normalized units. First define the following:

$$\begin{array}{cc}\hfill r& :=y/R\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill {\lambda }_c& :=Vcos(\beta )/(\mathsf{\Omega }R)\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill {\lambda }_i& :=v_i/(\mathsf{\Omega }R)\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill \mu & :=Vsin(\beta )/(\mathsf{\Omega }R)\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill \lambda & :={\lambda }_c+{\lambda }_i\hfill \end{array}$$

(9)

where $\mu$ is known as the advance ratio, ${\lambda }_c$ the climb ratio, and ${\lambda }_i$ the induced inflow ratio [34]. Thus by dividing both $U_{\Vert }$ and $U_{\perp }$ in (4) by $\mathsf{\Omega }R$, (4) becomes

$$\begin{array}{c}\hfill \varphi ({\lambda }_c,\mu ,{\lambda }_i,r,\psi )=arctan2\left(\lambda ,r+\mu sin(\psi )\right)\end{array}$$

(10)

Occasionally functions will be overloaded as such, and it should be clear from context (i.e., the input variables) which function is being referred to. Henceforth the approximation that $U_{\Vert }\gg U_{\perp }$ is made, such that

$$\begin{array}{c}\hfill \varphi ({\lambda }_c,\mu ,{\lambda }_i,r,\psi )=\frac{\lambda }{r+\mu sin(\psi )}\end{array}$$

(11)

This assumption is not true everywhere on the rotor disk (i.e. for all r and $\psi$) and for all ${\lambda }_c,\mu$, and a corresponding discussion is provided in Section 2.8. Nevertheless, this assumption is used in order to develop low order, computationally efficient maps. The local angle of attack, $\alpha$, of the infinitesimal blade element is then given by

$$\begin{array}{cc}\hfill \alpha ({\lambda }_c,\mu ,{\lambda }_i,r,\psi )& =\theta (r)-\varphi ({\lambda }_c,\mu ,{\lambda }_i,r,\psi )\hfill \end{array}$$

(12)

where $\theta (r)$ is the pitch angle of the blade element located at a distance $y=Rr$ from the centre.

Under the quasi-steady flow assumption, and again under the assumption that $U_{\Vert }\gg U_{\perp }$, the aerodynamic lift, drag, and pitching moment of the blade element are governed by the following standard formulae [70]:

$$\begin{array}{cc}\hfill \mathrm{d}L(\mathsf{\Omega },V,\beta ,y,\psi ,v_i)& \approx \frac{1}{2}\rho U_{\Vert }{(\mathsf{\Omega },V,\beta ,y,\psi )}^2{C}_L(\alpha (\mathsf{\Omega },V,\beta ,y,\psi ,v_i))c(y/R)\mathrm{d}y\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill \mathrm{d}D(\mathsf{\Omega },V,\beta ,y,\psi ,v_i)& \approx \frac{1}{2}\rho U_{\Vert }{(\mathsf{\Omega },V,\beta ,y,\psi )}^2{C}_D(\alpha (\mathsf{\Omega },V,\beta ,y,\psi ,v_i))c(y/R)\mathrm{d}y\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill \mathrm{d}M(\mathsf{\Omega },V,\beta ,y,\psi ,v_i)& \approx \frac{1}{2}\rho U_{\Vert }{(\mathsf{\Omega },V,\beta ,y,\psi )}^2{C}_M(\alpha (\mathsf{\Omega },V,\beta ,y,\psi ,v_i))c{(y/R)}^2\mathrm{d}y\hfill \end{array}$$

(15)

where $\rho$ is the air density and $c(y/R)$ is the chord length of the blade element located a distance y from the centre of the propeller. The above can be normalized to yield the loads in dimensionless units:

$$\begin{array}{cc}\hfill \mathrm{d}{L}_N({\lambda }_c,\mu ,r,\psi ,{\lambda }_i)& :=\frac{\mathrm{d}L(\mathsf{\Omega },V,\beta ,y,\psi ,v_i)}{\frac{1}{2}\rho A{(\mathsf{\Omega }R)}^2}=\frac{c(r)}{\pi R}{(r+\mu sin(\psi ))}^2{C}_L(\alpha ({\lambda }_c,\mu ,{\lambda }_i,r,\psi ))\mathrm{d}r\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill \mathrm{d}{D}_N({\lambda }_c,\mu ,r,\psi ,{\lambda }_i)& :=\frac{\mathrm{d}L(\mathsf{\Omega },V,\beta ,y,\psi ,v_i)}{\frac{1}{2}\rho A{(\mathsf{\Omega }R)}^2}=\frac{c(r)}{\pi R}{(r+\mu sin(\psi ))}^2{C}_D(\alpha ({\lambda }_c,\mu ,{\lambda }_i,r,\psi ))\mathrm{d}r\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill \mathrm{d}{M}_N({\lambda }_c,\mu ,r,\psi ,{\lambda }_i)& :=\frac{\mathrm{d}L(\mathsf{\Omega },V,\beta ,y,\psi ,v_i)}{\frac{1}{2}\rho A{(\mathsf{\Omega }R)}^{2}R}=\frac{c{(r)}^2}{\pi R^2}{(r+\mu sin(\psi ))}^2{C}_M(\alpha ({\lambda }_c,\mu ,{\lambda }_i,r,\psi ))\mathrm{d}r\hfill \end{array}$$

(18)

where $A=\pi R^2$ is the rotor disk area.

The lift, drag, and pitching moment coefficients are assumed to be of the form

$$\begin{array}{cc}\hfill C_L(\alpha )& =c_{l,0}+c_{l,\alpha }\alpha \hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill C_D(\alpha )& =c_{d,0}+c_{d,\alpha }{\alpha }^2\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill C_M(\alpha )& =c_{m,0}+c_{m,\alpha }\alpha \hfill \end{array}$$

(21)

The $c_{l,0}$ and $c_{m,0}$ terms are needed as the airfoils for UAV propellers are typically very positively cambered [70]. Furthermore, such models may not be valid for high-pitch propellers operating at low speeds, thereby operating in the stall regime; an approach similar to [15] could be used, but would then result in more computationally complex models.

We must also assume a form for the propeller geometry, that is, $\theta (·)$ and $c(·)$. Henceforth the following will be used:

$$\begin{array}{cc}\hfill \theta (r)& =\left\{\begin{array}{cc}\frac{{\theta }_{\mathrm{tip}}}{r}\hfill & 1\ge r\ge \delta \hfill \\ 0\hfill & \mathrm{else}\hfill \end{array}\right.\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill c(r)& =\left\{\begin{array}{cc}\frac{c_{\mathrm{tip}}}{r}\hfill & 1\ge r\ge \delta \hfill \\ 0\hfill & \mathrm{else}\hfill \end{array}\right.\hfill \end{array}$$

(23)

where $\delta \in (0,1)$ is a parameter that represents the fraction of the propeller blade that is “not useful” [34]. The inverse relationship represents the ideal geometry for minimizing power consumption for hover and axial flight [34]. This chord model, however, is not the case for some propellers, notably APC’s slow-fly series, or micro UAV propellers that typically have a constant chord model. Thus, one could use another parametrization, e.g., as in [40] which uses a linear twist profile, instead of the ones above using additional parameters, or use a specific model for a specific propeller. Nevertheless, (22) and (23) are used for simplicity.

2.1. Thrust $F_T$

The infinitesimal thrust of the rotor, in dimensionless units, is given by

$$\begin{array}{c}\hfill N_b(\mathrm{d}{L}_{N}cos(\varphi )-\mathrm{d}{D}_{N}sin(\varphi ))\approx N_b\mathrm{d}{L}_N\end{array}$$

(24)

where $N_b$ is the number of blades the propeller has, and the approximation on the right-hand side comes from assuming $\mathrm{d}L\gg \mathrm{d}D$, and enforcing the prior assumption that $\varphi$ is small as in (11). Integrating the above with respect to r yields the normalized thrust $C_{FT}$ as a function of the azimuth angle $\psi$:

$$\begin{array}{cc}\hfill C_{FT}({\lambda }_c,\mu ,{\lambda }_i,\psi )& =N_b{\int }_0^1\frac{\mathrm{d}{L}_n({\lambda }_c,\mu ,r,\psi ,{\lambda }_i)}{\mathrm{d}r}\mathrm{d}r\hfill \end{array}$$

(25)

However, in general, knowing the loads as a function of $\psi$ is not so interesting, as the propeller rotates at high rates; one generally cares about the average thrust produced (although it is important to keep this in mind, as the varying loads can excite vibrational modes of a system [71,72], and may be observed using an approach as in [73]). Thus the average thrust over a complete rotation of the propeller is given by

$$\begin{array}{cc}\hfill C_{FT}({\lambda }_c,\mu ,{\lambda }_i)& =\frac{1}{2\pi }{\int }_0^{2\pi }{C}_{FT}({\lambda }_c,\mu ,{\lambda }_i,\psi )\mathrm{d}\psi \hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & =\frac{1}{2\delta }\sigma \left((1-\delta )\left(c_{l,0}\delta (1+\delta )-2c_{l,\alpha }\delta (\lambda -{\theta }_{\mathrm{tip}})+c_{l,\alpha }{\mu }^2{\theta }_{\mathrm{tip}}\right)-c_{l,0}\delta {\mu }^{2}ln(\delta )\right)\hfill \end{array}$$

(27)

where $\sigma :=\frac{N_b{c}_{\mathrm{tip}}}{\pi R}$ is the solidity ratio [34].

Note that the average thrust in dimensioned units can be recovered by multiplying by the normalization constant:

$$\begin{array}{cc}\hfill F_T(\mathsf{\Omega },V,\beta ,v_i)& =\frac{1}{2}\rho \pi R^2{(\mathsf{\Omega }R)}^2{C}_{FT}({\lambda }_c,\mu ,{\lambda }_i)\hfill \end{array}$$

(28)

In Section 2.6, the induced inflow $v_i\sim {\lambda }_i$ will be determined analytically as a function of $\mathsf{\Omega },V,\beta$, so as to conform with the goal (1).

2.2. H-Force $F_H$

The infinitesimal H-force, in dimensionless units, is given by

$$\begin{array}{c}\hfill N_b\left(\mathrm{d}{L}_{N}sin(\varphi )+\mathrm{d}{D}_{N}cos(\varphi )\right)sin(\psi )\approx N_b\left(\mathrm{d}{L}_N\varphi +\mathrm{d}{D}_N\right)sin(\psi )\end{array}$$

(29)

where the usual approximations are applied to yield the right hand side. Integrating with respect to r yields the normalized H-force $C_{FH}$ as a function of $\psi$:

$$\begin{array}{cc}\hfill C_{FH}({\lambda }_c,\mu ,{\lambda }_i,\psi )& =N_b{\int }_0^1\left(\frac{\mathrm{d}{L}_N({\lambda }_c,\mu ,{\lambda }_i,r,\psi )}{\mathrm{d}r}\varphi ({\lambda }_c,\mu ,{\lambda }_i,r,\psi )+\frac{\mathrm{d}{D}_N({\lambda }_c,\mu ,{\lambda }_i,r,\psi )}{\mathrm{d}r}\right)\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill & sin(\psi ({\lambda }_c,\mu ,{\lambda }_i,r,\psi ))\mathrm{d}r\hfill \end{array}$$

(31)

The average H-force over a complete rotation of the propeller is given by

$$\begin{array}{cc}\hfill C_{FH}({\lambda }_c,\mu ,{\lambda }_i)& =\frac{1}{2\pi }{\int }_0^{2\pi }{C}_{FH}({\lambda }_c,\mu ,{\lambda }_i,\psi )\mathrm{d}\psi \hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill & =\frac{1}{2\delta }\mu \sigma \left((1-\delta )\left(2c_{d,0}\delta +{\theta }_{\mathrm{tip}}\left((c_{l,\alpha }-2c_{d,\alpha })\lambda +2c_{d,\alpha }{\theta }_{\mathrm{tip}}\right)\right)-c_{l,0}\delta \lambda ln(\delta )\right)\hfill \end{array}$$

(33)

Similarly, the lateral force $F_S$ given by $\left(\mathrm{d}Lsin(\varphi )+\mathrm{d}Dcos(\varphi )\right)cos(\psi )\approx \left(\mathrm{d}L\varphi +\mathrm{d}D\right)cos(\psi )$ can be shown to be 0 on average (for a constant ${\lambda }_i$ across the rotor disk as in this case).

2.3. Rotor Torque $M_Q$

The infinitesimal rotor torque, in dimensionless units, is given by

$$\begin{array}{c}\hfill N_b\left(\mathrm{d}{L}_{N}sin(\varphi )+\mathrm{d}{D}_{N}cos(\varphi )\right)r\approx N_b\left(\mathrm{d}{L}_N\varphi +\mathrm{d}{D}_N\right)r\end{array}$$

(34)

Integrating with respect to r yields the normalized rotor torque $C_{MQ}$ as a function of $\psi$:

$$\begin{array}{cc}\hfill C_{MQ}({\lambda }_c,\mu ,{\lambda }_i,\psi )& =N_b{\int }_0^1\left(\frac{\mathrm{d}{L}_N({\lambda }_c,\mu ,{\lambda }_i,r,\psi )}{\mathrm{d}r}\varphi ({\lambda }_c,\mu ,{\lambda }_i,r,\psi )+\frac{\mathrm{d}{D}_N({\lambda }_c,\mu ,{\lambda }_i,r,\psi )}{\mathrm{d}r}\right)r\mathrm{d}r\hfill \end{array}$$

(35)

The average rotor torque over a complete rotation of the propeller is given by

$$\begin{array}{cc}\hfill C_{MQ}({\lambda }_c,\mu ,{\lambda }_i)& =\frac{1}{2\pi }{\int }_0^{2\pi }{C}_{MQ}({\lambda }_c,\mu ,{\lambda }_i,\psi )\mathrm{d}\psi \hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill & =\frac{1}{6}(1-\delta )\sigma \left(2c_{d,0}\left(1+\delta +{\delta }^2\right)+3c_{l,0}(\delta +1)\lambda +\right.\hfill \end{array}$$

(37)

$$\begin{array}{c}\left.6\left(c_{d,\alpha }(\lambda -{\theta }_{\mathrm{tip}})-c_{l,\alpha }\lambda \right)(\lambda -{\theta }_{\mathrm{tip}})+\frac{3{\mu }^2\left(c_{d,0}\delta +c_{d,\alpha }{\theta }_{\mathrm{tip}}^2\right)}{\delta }\right)\hfill \end{array}$$

(38)

2.4. Rolling Moment $M_R$

The infinitesimal rolling moment, in dimensionless units, is given by

$$\begin{array}{c}\hfill N_b\left(\mathrm{d}{L}_{N}cos(\varphi )-\mathrm{d}{D}_{N}sin(\varphi )\right)rsin(\psi )\approx N_b\mathrm{d}{L}_{N}rsin(\psi )\end{array}$$

(39)

Integrating with respect to r yields the normalized rolling moment $C_{MR}$ as a function of $\psi$:

$$\begin{array}{cc}\hfill C_{MR}({\lambda }_c,\mu ,{\lambda }_i,\psi )& =N_b{\int }_0^1\frac{\mathrm{d}{L}_N({\lambda }_c,\mu ,{\lambda }_i,r,\psi )}{\mathrm{d}r}rsin(\psi ({\lambda }_c,\mu ,{\lambda }_i,r,\psi ))\mathrm{d}r\hfill \end{array}$$

(40)

The average rolling moment over a complete rotation of the propeller is given by

$$\begin{array}{cc}\hfill C_{MR}({\lambda }_c,\mu ,{\lambda }_i)& =\frac{1}{2\pi }{\int }_0^{2\pi }{C}_{MR}({\lambda }_c,\mu ,{\lambda }_i,\psi )\mathrm{d}\psi \hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill & =\frac{1}{2}(1-\delta )\sigma \mu \left(c_{l,0}(\delta +1)-c_{l,\alpha }(\lambda -2{\theta }_{\mathrm{tip}})\right)\hfill \end{array}$$

(42)

2.5. Pitching Moment $M_P$

The infinitesimal pitching moment, in dimensionless units, is given by

$$\begin{array}{c}\hfill N_b\left(\mathrm{d}{M}_{N}sin(\psi )-(\mathrm{d}{L}_{N}cos(\varphi )-\mathrm{d}{D}_{N}sin(\varphi )rcos(\psi )\right)\approx N_b\left(\mathrm{d}{M}_{N}sin(\psi )-\mathrm{d}{L}_{N}rcos(\psi )\right)\end{array}$$

(43)

Integrating with respect to r yields the normalized pitching moment $C_{MR}$ as a function of $\psi$:

$$\begin{array}{cc}\hfill C_{MP}({\lambda }_c,\mu ,{\lambda }_i,\psi )& =N_b{\int }_0^1\left(\frac{\mathrm{d}{M}_N({\lambda }_c,\mu ,{\lambda }_i,r,\psi )}{\mathrm{d}r}sin(\psi ({\lambda }_c,\mu ,{\lambda }_i,r,\psi ))-\right.\hfill \end{array}$$

(44)

$$\begin{array}{c}\left.\frac{\mathrm{d}{L}_N({\lambda }_c,\mu ,{\lambda }_i,r,\psi )}{\mathrm{d}r}rcos(\psi ({\lambda }_c,\mu ,{\lambda }_i,r,\psi ))\right)\mathrm{d}r\hfill \end{array}$$

(45)

The average pitching moment over a complete rotation of the propeller is given by

$$\begin{array}{cc}\hfill C_{MP}({\lambda }_c,\mu ,{\lambda }_i)& =\frac{1}{2\pi }{\int }_0^{2\pi }{C}_{MP}({\lambda }_c,\mu ,{\lambda }_i,\psi )\mathrm{d}\psi \hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill & =\frac{c_{\mathrm{tip}}}{2\delta R}\sigma \mu \left(c_{m,\alpha }(\delta -1)(\lambda -2{\theta }_{\mathrm{tip}})-2c_{m,0}\delta ln(\delta )\right)\hfill \end{array}$$

(47)

2.6. Induced Inflow ${\lambda }_i$

A two-dimensional Eulerian control volume analysis [70] is used to determine the induced inflow ratio ${\lambda }_i$ (see Figure 3), assuming a steady, adiabatic and isentropic process (i.e., neglecting viscous effects). It is important to be aware that assuming an isentropic flow is not a good assumption when there is drag, however, only an approximation is sought here. Note that the control volume herein differs from the approaches in the literature, which use the Glauert flow model (which itself has no rigorous basis for its use [34]) which in the end yields an implicit equation for the induced inflow $v_i$, for which no closed form expression exists.

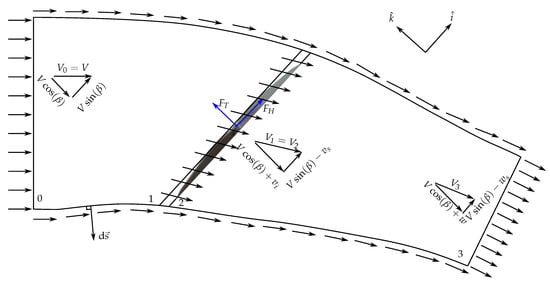
Figure 3. Two-dimensional Eulerian control volume applied to a propeller in forward flight conditions. The vector $\mathrm{d}\overrightarrow{s}$ represents an infinitesimal surface area of the control volume, whose direction is outwards.

The mass flow rate is

$$\begin{array}{cc}\hfill \dot{m}& ={\int \int }_0\rho ⟨\overrightarrow{v},\mathrm{d}\overrightarrow{s}⟩={\int \int }_2\rho ⟨\overrightarrow{v},\mathrm{d}\overrightarrow{s}⟩={\int \int }_3\rho ⟨\overrightarrow{v},\mathrm{d}\overrightarrow{s}⟩\hfill \end{array}$$

(48)

$$\begin{array}{cc}\hfill & =\rho A_{0}V=\rho A(v_i+Vcos(\beta ))=\rho A_3{V}_3\hfill \end{array}$$

(49)

Applying the conservation of momentum on the entire control volume, neglecting gravitational effects on the fluid, and assuming constant static pressure around the entire control volume, we have in the thrust direction $\widehat{k}$

$$\begin{array}{cc}\hfill F_T^{\mathrm{mt}}& =-{\int \int }_S\rho ⟨\overrightarrow{v},\mathrm{d}\overrightarrow{s}⟩⟨\overrightarrow{v},\widehat{k}⟩\hfill \end{array}$$

(50)

$$\begin{array}{cc}\hfill & =-{\int \int }_3\rho ⟨\overrightarrow{v},\mathrm{d}\overrightarrow{s}⟩⟨\overrightarrow{v},\widehat{k}⟩-{\int \int }_0\rho ⟨\overrightarrow{v},\mathrm{d}\overrightarrow{s}⟩⟨\overrightarrow{v},\widehat{k}⟩\hfill \end{array}$$

(51)

$$\begin{array}{cc}\hfill & =\rho A_3{V}_3(w+Vcos(\beta ))+\rho A_{0}V(Vcos(\beta ))\hfill \end{array}$$

(52)

$$\begin{array}{cc}\hfill & =\dot{m}w\hfill \end{array}$$

(53)

and similarly in the drag direction $\widehat{i}$

$$\begin{array}{cc}\hfill F_H^{\mathrm{mt}}& =-{\int \int }_S\rho ⟨\overrightarrow{v},\mathrm{d}\overrightarrow{s}⟩⟨\overrightarrow{v},\widehat{i}⟩\hfill \end{array}$$

(54)

$$\begin{array}{cc}\hfill & =-{\int \int }_3\rho ⟨\overrightarrow{v},\mathrm{d}\overrightarrow{s}⟩⟨\overrightarrow{v},\widehat{i}⟩-{\int \int }_0\rho ⟨\overrightarrow{v},\mathrm{d}s⟩⟨\overrightarrow{v},\widehat{i}⟩\hfill \end{array}$$

(55)

$$\begin{array}{cc}\hfill & =-\rho A_3{V}_3(Vsin(\beta )-w_s)+\rho A_{0}V(Vsin(\beta ))\hfill \end{array}$$

(56)

$$\begin{array}{cc}\hfill & =\dot{m}{w}_s\hfill \end{array}$$

(57)

Now applying the conservation of energy:

$$\begin{array}{cc}\hfill F_T^{\mathrm{mt}}(Vcos(\beta )+v_i)-F_H^{\mathrm{mt}}(Vsin(\beta )-v_s)& ={\int \int }_S\frac{1}{2}\rho ⟨\overrightarrow{v},\mathrm{d}\overrightarrow{s}⟩v^2\hfill \end{array}$$

(58)

$$\begin{array}{cc}\hfill & ={\int \int }_3\frac{1}{2}\rho ⟨\overrightarrow{v},\mathrm{d}\overrightarrow{s}⟩v^2+{\int \int }_0\frac{1}{2}\rho ⟨\overrightarrow{v},\mathrm{d}\overrightarrow{s}⟩v^2\hfill \end{array}$$

(59)

$$\begin{array}{cc}\hfill & =\frac{1}{2}\rho A_3{V}_3^3-\frac{1}{2}\rho A_0{V}^3\hfill \end{array}$$

(60)

$$\begin{array}{cc}\hfill & =\frac{1}{2}\dot{m}(V_3^2-V^2)\hfill \end{array}$$

(61)

$$\begin{array}{cc}\hfill & =\frac{1}{2}\dot{m}(w^2+w_s^2+2Vcos(\beta )w-2Vsin(\beta )w_s)\hfill \end{array}$$

(62)

Combining (53), (57) and (62) yields

$$\begin{array}{cc}\hfill 2(w{v}_i+w_s{v}_s)& =w^2+w_s^2\hfill \end{array}$$

(63)

$$\begin{array}{cc}\hfill \Rightarrow 2v_i& \approx w\hfill \end{array}$$

(64)

where the approximation results from assuming that $w\gg w_s$ and $v_i\gg v_s$, which is equivalent to assuming that the rotor thrust is much larger than the H-force. From Supplementary Dataset S1 (or Figure 6), this is the case as the thrust is an order of magnitude larger than the H-force, consistent with the observations in [65] (and it is worth mentioning, the H-force is about an order of magnitude larger than the lateral force $F_S$). Thus,

$$\begin{array}{cc}\hfill F_T^{\mathrm{mt}}& =2\rho A(v_i+Vcos(\beta ))v_i\hfill \end{array}$$

(65)

or in the normalized form

$$\begin{array}{c}\hfill \frac{F_T^{\mathrm{mt}}}{\frac{1}{2}\rho A{(\mathsf{\Omega }R)}^2}=4({\lambda }_i+{\lambda }_c){\lambda }_i=:C_{FT}^{\mathrm{mt}}({\lambda }_c,{\lambda }_i)\end{array}$$

(66)

Therefore, ${\lambda }_i$ can be solved for via the following:

$$\begin{array}{c}\hfill {\lambda }_i({\lambda }_c,\mu )=find{\lambda }_i\mathrm{s}.\mathrm{t}.C_{FT}({\lambda }_c,\mu ,{\lambda }_i)=C_{FT}^{\mathrm{mt}}({\lambda }_c,{\lambda }_i)\end{array}$$

(67)

yielding

$$\begin{array}{cc}\hfill {\lambda }_i({\lambda }_c,\mu )& =\frac{1}{8}\left(-4{\lambda }_c+c_{l,\alpha }\sigma (\delta -1)+[16{\lambda }_c^2+8c_{l,\alpha }(\delta -1){\lambda }_c\sigma +\right.\hfill \end{array}$$

(68)

$$\begin{array}{c}\left.\frac{1}{\delta }(\delta -1)\sigma \left(-8c_{l,0}\delta (1+\delta )+c_{l,\alpha }\left(c_{l,\alpha }(\delta -1)\delta \sigma -8\left(2\delta +{\mu }^2\right){\theta }_{\mathrm{tip}}\right)\right)-8c_{l,0}{\mu }^2\sigma ln(\delta ){]}^{1/2}\right)\hfill \end{array}$$

(69)

2.7. Summary

In light of the inflow mapping (68), with abuse of notation we define

$$\begin{array}{c}\hfill C_{FT}({\lambda }_c,\mu ):=C_{FT}({\lambda }_c,\mu ,{\lambda }_i({\lambda }_c,\mu ))\end{array}$$

(70)

and similarly for the remaining normalized force and torque maps. Furthermore, let x define the parameter vector that parametrizes the above models:

$$\begin{array}{c}\hfill x:=(c_{l,0},c_{l,\alpha },c_{d,0},c_{d,\alpha },c_{m,0},c_{m,\alpha },\delta ,{\theta }_{\mathrm{tip}},c_{\mathrm{tip}})\end{array}$$

(71)

Thus, to make it clear that the maps are actually parametrized by x, a superscript will be used as follows:

$$\begin{array}{c}\hfill C_{FT}^x({\lambda }_c,\mu )\end{array}$$

(72)

Therefore, the model for (1) can be summarized as follows:

$$\begin{array}{c}\hfill (\mathsf{\Omega },V,\beta )\mapsto \left[\begin{array}{c}{F}_T\\ F_H\\ M_Q\\ M_R\\ M_P\end{array}\right]=\left[\begin{array}{c}{C}_{FT}^x({\lambda }_c,\mu )\frac{1}{2}\rho \pi R^2{(\mathsf{\Omega }R)}^2\\ C_{FH}^x({\lambda }_c,\mu )\frac{1}{2}\rho \pi R^2{(\mathsf{\Omega }R)}^2\\ C_{MQ}^x({\lambda }_c,\mu )\frac{1}{2}\rho \pi R^2{(\mathsf{\Omega }R)}^{2}R\\ C_{MR}^x({\lambda }_c,\mu )\frac{1}{2}\rho \pi R^2{(\mathsf{\Omega }R)}^{2}R\\ C_{MP}^x({\lambda }_c,\mu )\frac{1}{2}\rho \pi R^2{(\mathsf{\Omega }R)}^{2}R\end{array}\right],\begin{array}{cc}\hfill {\lambda }_c& =\frac{Vcos(\beta )}{\mathsf{\Omega }R}\hfill \\ \hfill \mu & =\frac{Vsin(\beta )}{\mathsf{\Omega }R}\hfill \end{array}\end{array}$$

(73)

2.8. Check if the Assumption $\varphi$ is Small is Violated

Now that the inflow mapping (68) has been solved for, the goal here is to check if we have contradicted our small-angle approximation to simplify the flow angle $\varphi$ from (10) to (11). This will be done by plotting the values of $\varphi$ using (10), which is a function of ${\lambda }_i$ for which (68) is used, as a heat map over the rotor disk. This is done for four different combinations of operating conditions in $({\lambda }_c,\mu )$, as done in Figure 4. The largest value of ${\lambda }_c$ and $\mu$ chosen is 0.2, as ${\lambda }_c\approx 0.2$ roughly corresponds to when UAV propellers produce zero thrust (see Section 3.2 for examples), an already extreme operating condition. If there are large portions of the rotor disk where the small-angle assumption is violated, then we can necessarily say that our proposed model (73) is invalid.

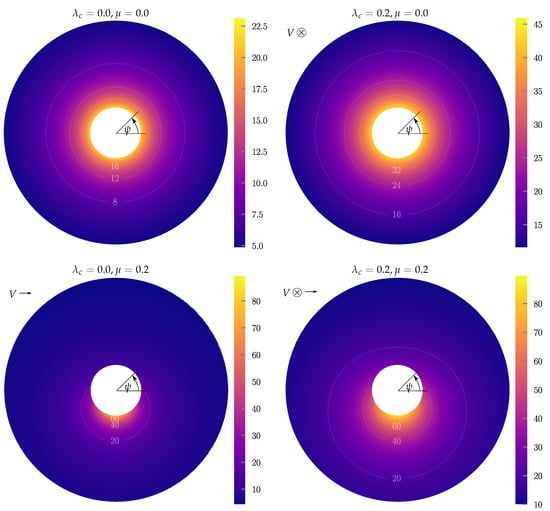
Figure 4. Heat map of the flow angles $\varphi$ (in degrees) over the rotor disk (top view), evaluated using the exact map (10) with ${\lambda }_i$ from (68) for four different operating conditions in $({\lambda }_c,\mu )$. For ${\lambda }_c>0$, the incoming flow goes into the page, and for $\mu >0$, the incoming flow comes from the left. The relevant parameter values used are $c_{l,0}=0.4,c_{l,\alpha }=3,\delta =0.2,\sigma =0.084$, which are typical values for UAV propellers (see Appendix A). The goal is to have an idea of the flow angles, and whether we contradict our small-angle approximation used in (11).

As can be seen in Figure 4, for hover flight (${\lambda }_c=0,\mu =0$) the angle reaches approximately 22 degrees, which is small enough for the small-angle approximation to hold. In the extreme axial flight scenario (${\lambda }_c=0.2,\mu =0$), the angle reaches above 40 degrees, which violates the small-angle approximation, but this occurs in a relatively small region of the rotor disk. The same is also true for the oblique flow scenario ($\mu =0.2$). Nevertheless, the region in which the violation occurs will become larger as ${\lambda }_c$ and $\mu$ increases. It is also interesting to note that the angle doesn’t reach near $180[\mathrm{deg}]$, the “reverse flow region” [36], unless $\mu$ is (roughly) larger than 0.5. Thus we can conclude that for the operating regions considered, the proposed model (73) is not invalid, but the error of the model can become substantial for larger ${\lambda }_c$ and $\mu$.

3. Inferring Parameters from Labelled Data (Supervised Learning)

The goal in this section is two-fold: to determine the parameter vector x for the model (73) using labelled data, and to assess the fidelity of the corresponding model.

3.1. Algorithm

Let any variable with a bar denote a vector of measurements. For example, $\overline{\mathsf{\Omega }}\in {\mathbb{R}}^{N_m}$ is a tuple of $N_m$ measured $\mathsf{\Omega }$ values, and ${\overline{\mathsf{\Omega }}}_i$ is the i-th measured value. Similarly, the i-th measured force coefficient is given as ${\overline{C}}_{y,i}:=\overline{y_i}/\frac{1}{2}\rho A{({\overline{\mathsf{\Omega }}}_{i}R)}^2$ for $y\in \left\{F_T,F_H\right\}$, and for the moment coefficient is given as ${\overline{C}}_{y,i}:=\overline{y_i}/\frac{1}{2}\rho A{({\overline{\mathsf{\Omega }}}_{i}R)}^{2}R$ for $y\in \left\{M_Q,M_R,M_P\right\}$.

The measured root mean square error for the force/moment coefficient of $y\in \left\{F_T,F_H,M_Q,M_R,M_P\right\}$ is

$$\begin{array}{cc}\hfill RMS{E}_y(x)& :=\sqrt{\frac{1}{N_m}{\displaystyle \sum _{i=1}^{N_m}}{\left(C_y^x({\overline{{\lambda }_c}}_i,{\overline{\mu }}_i)-{\overline{C}}_{y,i}\right)}^2}\hfill \end{array}$$

(74)

Thus the optimization algorithm to infer the parameters x is simply

$$\begin{array}{c}\hfill x^{*}=\underset{x}{argmin}\sum _{y\in \left\{Ft,Fd,Mq,Mr,Mp\right\}}RMS{E}_y(x)\end{array}$$

(75)

This problem is not convex (the model is not linear in the parameters x), and is solved in practice using Python’s SciPy package [74] via the Differential Evolution optimization routine from [75] (the settings given to the scipy.optimize.differential_evolution routine are: popsize=200, polish=True, workers=-1, bounds=[(0,1), (1,10), (0,0.5), (0,5), (-10,10), (0,30), (0.1,0.4), (0, numpy.radians(30)), (0.01*R,0.3*R)]. The bounds were added to limit the search space in order to speed up convergence. The optimization procedure runs for approximately 2 minutes using measurements as outlined in Section 3.2 on a laptop with an Intel i7-6700HQ processor).

To assess the quality of the fit, the standard metrics outlined in [76,77] are used: the coefficient of determination $R^2$:

$$\begin{array}{cc}\hfill R_y^2(x)& =1-\frac{RMS{E}_y{(x)}^2}{\mathrm{SampleVariance}({\overline{C}}_y)}\hfill \end{array}$$

(76)

and the normalized root-mean-squared-error (nRMSE):

$$\begin{array}{c}\hfill nRMS{E}_y(x)=\frac{RMS{E}_y(x)}{{max}_i{\overline{C}}_{y,i}-{min}_i{\overline{C}}_{y,i}}\end{array}$$

(77)

3.2. Experimental Assessment

3.2.1. Oblique Flow Results

Two datasets for oblique flows are used. The first contains load measurements at various operating conditions $V,\mathsf{\Omega }$ and $\beta$ for 19 propellers collected at the “Large Subsonic Wind Tunnel” at the Institute of Fluid Dynamics at ETH Zurich (see Figure 5 for the experimental set-up). In particular, the tested wind speeds V were set between $0,6,18[\mathrm{m}/\mathrm{s}]$. At each given wind speed, the propeller rotation rate $\mathsf{\Omega }$ was set to vary sinusoidally at $1/60\approx 0.017[\mathrm{Hz}]$ between 150 and $600[\mathrm{rad}/\mathrm{s}]$. Meanwhile, the angle $\beta$ is varied with a servo motor at a rate of $0.2[\mathrm{deg}/\mathrm{s}]$ between $-10$ and $90[\mathrm{deg}]$. The low bandwidth in these operating conditions is assumed to be sufficiently small for the quasi-steady flow assumption to hold, and the torque resulting from the gyroscopic precession is negligible. Load data was collected at a rate of $1[\mathrm{kHz}]$, which is then passed through an ideal low pass filter in post-processing with cut-off $0.1[\mathrm{Hz}]$ to obtain the average loads, and then translated to the centre of the rotor disk (in particular, the moment caused by $F_H$ at the loadcell is removed from the measured pitching moment, to yield $M_P$). The resulting dataset can be found in Supplementary Dataset S1 (the samples in Supplementary Dataset S1 have been down-sampled to 50 [Hz] to reduce size; some propellers have data for $\beta >90[\mathrm{deg}]$).

Figure 5. Experimental set-up for oblique flow inside the “Large Subsonic Wind Tunnel” at ETH Zurich. The sting is mounted on a servo motor underneath the tunnel that rotates around the vertical axis to test various $\beta$ angles. The loads measured at the loadcell are translated to the centre of the propeller. The loadcell used is an ATI Mini40 with the SI-20-1 calibration, and communicates the load data to the host computer via a direct Ethernet connection. The propeller is rotated via a brushless DC motor that is driven by an SN20A electronic speed controller (ESC). The measured rotation rate $\mathsf{\Omega }$ based on the zero-phase crossings of the motor is computed by an STM32F4 microcontroller, which then communicates the $\mathsf{\Omega }$ to the host computer via a Laird RM024 radio. Both the wind speed V, which is measured using a pitot tube and pressure sensor, and servo angle $\beta$, are sampled via a LabJack U12 data acquisition board and sent to the host PC over a USB connection.

The data points corresponding to ${\lambda }_c>0.3$ and $\mu >0.3$ are thrown away (far too extreme of an operating condition and practically uninteresting), after which the grey-box identification is performed. Figure 6 shows the results for one of the tested propellers, and Figure 7 shows the same but in the dimensionless space. The plots for the rest of the tested propellers can be found in Supplementary Dataset S1. In Figure 6, the standard hover model is also shown for reference, which has clear mismatch for non-zero V.

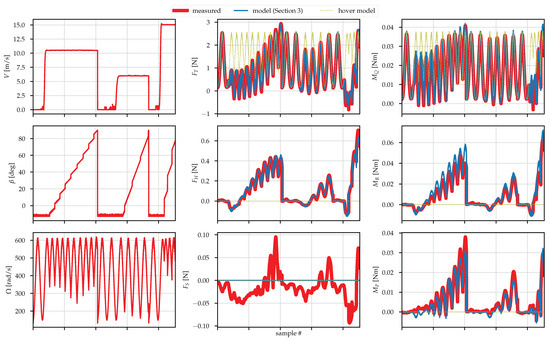
Figure 6. Propeller: mamr-8x4.5. Note that the points corresponding to ${\lambda }_c<0$, ${\lambda }_c>0.3$ and $\mu >0.3$ have been omitted, as mentioned in Section 3.2. Note that (1) neglects the side force $F_S$, so the model is set to output $0[\mathrm{N}]$. Model is as per Section 3. The prediction made by the standard hover model is also shown for reference.

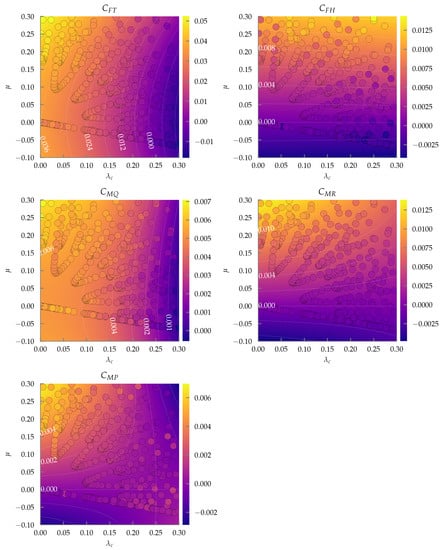
Figure 7. Propeller: mamr-8x4.5, in the dimensionless space. Measured data are shown as circles, and the fitted model as described in Section 3 is depicted as a contour plot with associated labelled contour lines.

The second dataset is provided by the authors of [7], who did a similar data collection of load data but for a single, Graupner electric 9x5 propeller. Figure 8 shows the corresponding plots.

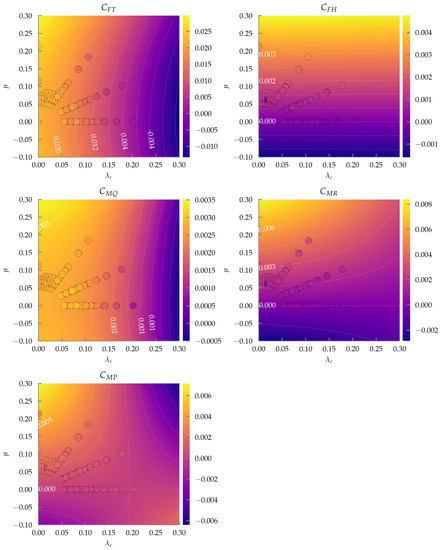
Figure 8. Propeller: gre-9x5, in the dimensionless space. Measured data from [7] are shown as circles, and the fitted model as described in Section 3 is depicted as a contour plot with associated labelled contour lines.

The fitting errors across the two datasets are depicted in Figure 9, and the results along with the optimal parameter values can be found in tabular format in Table A1 in Appendix A. A few observations can be made:

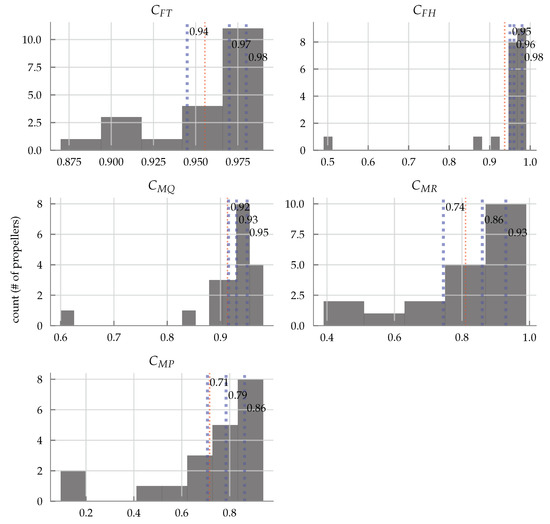
Figure 9. Histogram of $R^2$ values for each force and moment coefficient using the fitted model as described in Section 3 for all 20 propellers tested under oblique flow. The errors along with the parameter values can be found in tabular format in Table A1 in Appendix A. The blue dotted lines represent the 25, 50, and 75th percentiles and are labelled, and the red dotted line represents the mean.

• From the histograms in Figure 9, we can see that the models perform well, especially for the forces $F_T$, $F_H$ and the rotor torque $M_Q$ which have median $R^2$ values above 0.93 (an $R^2$ of 1 corresponds to perfect fit). The rolling and pitching moments have slightly reduced accuracy, with median $R^2$ of 0.86 and 0.79, respectively. However, the $R^2$ metric tends to underestimate the model performance when the data has small values [76], as is the case for the moment coefficients. The $nRMSE$ values found in Appendix A, or the plots in Supplementary Dataset S1, indeed shows that the model performance is still reasonable for the propellers that have poorer $R^2$ values.
• From the fitted parameter values in Appendix A, we can see that the parameters are in a consistent range of values for both datasets. Occasionally the fitted $c_{l,\alpha }$ value exceeds $2\pi$ (the theoretical value for a flat plate [70]), which can be expected for non-symmetric airfoils with positive camber [70]. Furthermore, the pitching moment constants $c_{m,0},c_{m,\alpha }$, are consistently large in magnitude. From thin airfoil theory, this could again be expected for airfoils with very large positive camber [70]; however, there could be some unmodelled phenomena, possibly due to blade flapping [34], or an artefact of the assumptions made to derive the map (73), and could be a subject for future investigation.

3.2.2. Axial flow Results

The same fitting procedure is performed against the dataset for axial flow provided by [68], and as such we only consider the thrust and rotor torque. Figure 10 show the plots for four out of the 180 propellers, and the histogram of fitting errors are shown in Figure 11. The parametric models perform very well, with a median $R^2$ value of above 0.97, and from Table A2 in Appendix A, there is good consistency with the range of parameter values.

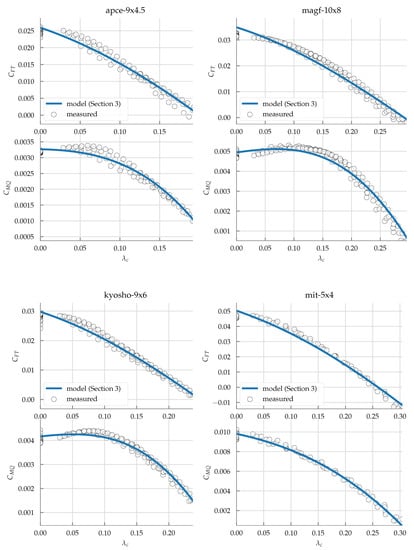
Figure 10. Models as described in Section 3 tested against measured data provided by [68] for four propellers.

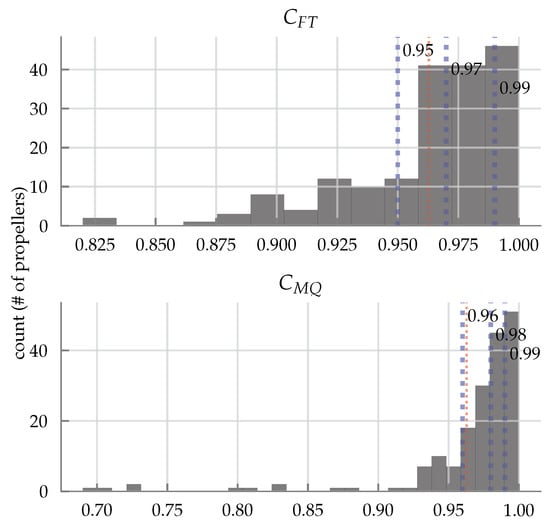
Figure 11. Histogram of $R^2$ values for each force and moment coefficient using the fitted model as described in Section 3 for the 180 propellers tested under axial flow from the dataset [68]. The errors along with the parameter values can be found in tabular format in Table A2 in Appendix A. The blue dotted lines represent the 25, 50, and 75th percentiles and are labelled, and the red dotted line represents the mean.

4. Inferring Parameters a-priori, without Labelled Data

The goal in this section is to infer the parameters x for the model (73) using only the static load coefficients to construct a prediction for the parameter vector x and to assess the corresponding model’s fidelity.

4.1. Parameter Prediction

Start by fixing $c_{d,0}=0.05$, about the average of the optimal fit values from Table A1 and Table A2 in Appendix A, and consistent with typical values in literature for airfoils [59,70]. Similarly, fix $\delta =0.20$, a typical value as used in [34]. The value $c_{\mathrm{tip}}$ is measured directly from the propeller. Some propellers have a sharp taper near the tips and it becomes difficult to define where to measure; we measured at the point just before it starts to taper off, around $r=0.93$.

Furthermore, assume that the airfoil of the blades is symmetric, and thus as a consequence fix $c_{l,0}=c_{m,0}=c_{m,\alpha }=0$ (we have no other information to infer these parameters).

The value of ${\theta }_{\mathrm{tip}}$ can be inferred: propellers are typically specified as $R\times P$, with R the radius of the propeller (usually in inches), and P is the mean geometric pitch (also usually in inches). The geometric pitch $p(r)$ is defined to be the amount a blade element at $y=Rr$ travels forward over one rotation of the propeller through a solid medium (i.e., without flow slippage) [78,79], and is given by the following geometric relationship (some manufacturers may use their own definition for the pitch, but nevertheless this is used as a starting point):

$$\begin{array}{cc}\hfill tan\left(\theta (r)\right)& =\frac{p(r)}{2\pi Rr}\hfill \end{array}$$

(78)

Thus the mean geometric pitch P is given by

$$\begin{array}{cc}\hfill P& ={\int }_0^{1}2\pi Rrtan(\theta (r))\mathrm{d}r\hfill \end{array}$$

(79)

Using our definition of $\theta (r)$ from (22),

$$\begin{array}{cc}\hfill P& =2\pi R{\int }_{\delta }^{1}rtan\left(\frac{{\theta }_{\mathrm{tip}}}{r}\right)\mathrm{d}r\hfill \end{array}$$

(80)

$$\begin{array}{cc}\hfill & \approx 2\pi R{\int }_{\delta }^1{\theta }_{\mathrm{tip}}\mathrm{d}r\hfill \end{array}$$

(81)

$$\begin{array}{cc}\hfill \Rightarrow {\theta }_{\mathrm{tip}}& =\frac{P}{2\pi R(1-\delta )}=1.25\frac{P}{2\pi R}\hfill \end{array}$$

(82)

It is interesting to note that the models are very sensitive to the ${\theta }_{\mathrm{tip}}$ value, and using even a slightly adjusted value to the one proposed in (82) can result in grossly inaccurate models.

Next assume that the static thrust and torque coefficients have been measured, using a procedure as in e.g., [80], i.e., by fitting the standard quadratic model with coefficients ${\alpha }_T,{\alpha }_Q$ at hover such that

$$\begin{array}{c}\hfill F_T(\mathsf{\Omega },V=0,\beta =\times )={\alpha }_T{\mathsf{\Omega }}^2\end{array}$$

(83)

$$\begin{array}{c}\hfill M_Q(\mathsf{\Omega },V=0,\beta =\times )={\alpha }_Q{\mathsf{\Omega }}^2\end{array}$$

(84)

The equivalent coefficients in normalized units are given by

$$\begin{array}{c}\hfill C_{FT}^{\mathrm{static}}:=\frac{{\alpha }_T}{\frac{1}{2}\rho \pi R^4}\end{array}$$

(85)

$$\begin{array}{c}\hfill C_{MQ}^{\mathrm{static}}:=\frac{{\alpha }_Q}{\frac{1}{2}\rho \pi R^5}\end{array}$$

(86)

The remaining coefficients to be determined are $c_{l,\alpha }$ and $c_{d,\alpha }$. These can be determined by using the static coefficients from (85) and (86) in a root finding routine as follows:

$$\begin{array}{cc}\hfill c_{l,\alpha }& =find{x}_1\mathrm{s}.\mathrm{t}.C_{FT}^x(0,0)=C_{FT}^{\mathrm{static}}\hfill \end{array}$$

(87)

$$\begin{array}{cc}\hfill c_{d,\alpha }& =find{x}_3\mathrm{s}.\mathrm{t}.C_{MQ}^x(0,0)=C_{MQ}^{\mathrm{static}}\hfill \end{array}$$

(88)

where $x_i$ denotes the i-th element of the parameter vector x. Note that (87) must be performed before (88), since the rotor torque map depends on the parameter $c_{l,\alpha }$. If a root cannot be found, then the above can be converted to a least squares optimization problem.

4.2. Experimental Assessment

4.2.1. Oblique Flow Results

The approach is tested against the two oblique flow datasets as described in Section 3.2; as before, the models can be viewed for one of the propellers in Figure 12 and Figure 13 (the plots for the remaining tested propellers are available in Supplementary Dataset S1), and the histogram of errors across all propellers can be found in Figure 14. A couple of observations can be made:

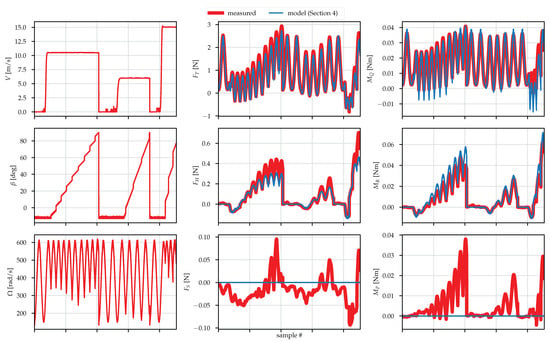
Figure 12. Propeller: mamr-8x4.5. Note that the points corresponding to ${\lambda }_c<0$, ${\lambda }_c>0.3$ and $\mu >0.3$ have been thrown away, as mentioned in Section 3.2. Note that (1) neglects the side force $F_S$, so the model is set to output $0[\mathrm{N}]$. Model is as per Section 4.

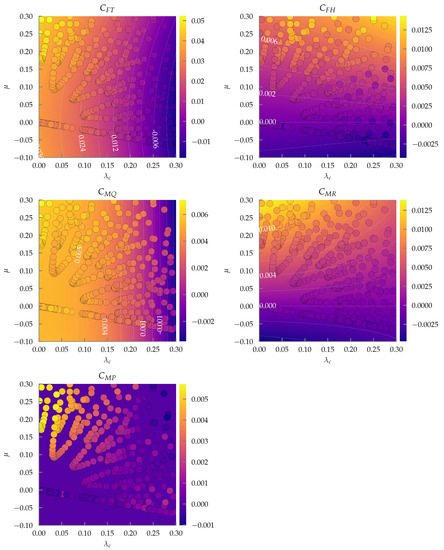
Figure 13. Propeller: mamr-8x4.5, in the dimensionless space. Measured data are shown as circles, and the model as described in Section 4 is depicted as a contour plot with associated labelled contour lines.

Figure 14. Histogram of $R^2$ values for each force and moment coefficient using the predicted model as described in Section 4 for all 20 propellers tested under oblique flow. The errors along with the parameter values can be found in tabular format in Table A3 in Appendix A. The blue dotted lines represent the 25, 50, and 75th percentiles and are labelled, and the red dotted line represents the mean.

• The thrust, H-force, and rolling moments have (surprisingly) high accuracy, with median $R^2$ values above 0.88.
• The rotor torque (median $R^2$ of 0.61) has reduced accuracy for few of the propellers, such as the apcsf, most likely due to severity in the mismatch of the assumed chord model (23). However, typically most of the error for the rotor torque comes at the high ${\lambda }_c,\mu$ ratios, as seen in Figure 12 and Figure 13: in Figure 12, the mismatch in torque occurs when the rotor is producing negative thrust, that is ${\lambda }_c$ near 0.3 in Figure 13. Thus for small enough operating conditions in ${\lambda }_c,\mu$, this approach may prove feasible for predicting the rotor torque as well. The pitching moments also have reduced accuracy (median $R^2$ of $-0.35$), as expected as assuming symmetric airfoils results in the predicted pitching moments to be identically equal to zero, which evidently is not the case.

4.2.2. Axial Flow Results

The same approach was tested against the database provided in [68] (not all propellers could be tested, since the chord measurements were not provided for all propellers). The histogram of the errors using the $R^2$ metric are shown in Figure 15.

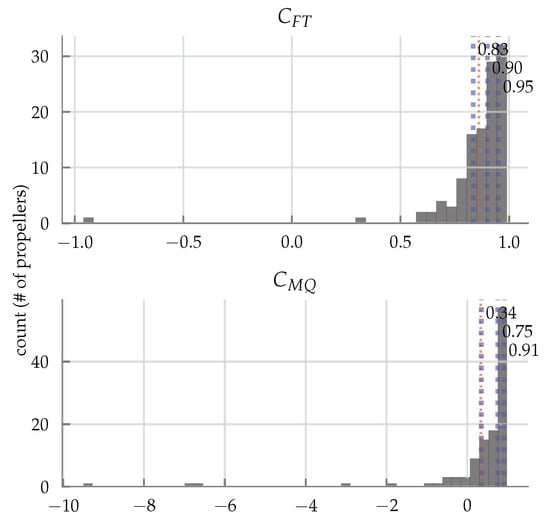
Figure 15. Histogram of $R^2$ values for each force and moment coefficient using the predicted model as described in Section 4 for 115 propellers tested under axial flow from the dataset [68]. The errors along with the parameter values can be found in tabular format in Table A4 in Appendix A. The blue dotted lines represent the 25, 50, and 75th percentiles and are labelled, and the red dotted line represents the mean.

Again, the results are surprisingly good (median $R^2$ for thrust is 0.90, and for the torque is 0.75). The propellers that do have issues are the APC slowfly propellers, as was the case for the oblique flow, as well as for some of the smaller propellers with diameter less than five inches (e.g., the small gwsdd and the mi propellers). This again can be attributed to the mismatch between the assumed chord model (23), as these small propeller blades usually have a constant chord model. This could be a subject for further investigation.

5. Second-Order Lumped Parameter Models

The goal in this section is to simplify the models of the load coefficients (73) even further using a second-order Taylor series expansion. This yields a lower-order, and yet even more computationally inexpensive model for the propeller loads, as the models become multinomials.

5.1. Models

First consider the thrust coefficient, $C_{FT}({\lambda }_c,\mu )$. The second-order Taylor expansion around $({\lambda }_c=0,\mu =0)$ yields:

$$\begin{array}{cc}\hfill C_{FT}({\lambda }_c,\mu )& \approx C_{FT}^{2\mathrm{nd}}({\lambda }_c,\mu ):=\underset{=C_{FT}^{\mathrm{static}}}{\underbrace{C_{FT}^x(0,0)}}+\left[\begin{array}{cc}\frac{\partial C_{FT}^x}{\partial {\lambda }_c}& \frac{\partial C_{FT}^x}{\partial \mu }\end{array}\right]\left[\begin{array}{c}{\lambda }_c\\ \mu \end{array}\right]+\frac{1}{2}\left[\begin{array}{cc}{\lambda }_c& \mu \end{array}\right]\left[\begin{array}{cc}\frac{{\partial }^2{C}_{FT}^x}{\partial {\lambda }_c^2}& \frac{{\partial }^2{C}_{FT}^x}{\partial {\lambda }_c\partial \mu }\\ \frac{{\partial }^2{C}_{FT}^x}{\partial {\lambda }_c\partial \mu }& \frac{{\partial }^2{C}_{FT}^x}{\partial {\mu }^2}\end{array}\right]\left[\begin{array}{c}{\lambda }_c\\ \mu \end{array}\right]\hfill \end{array}$$

(89)

where the partial derivatives in (89) are evaluated at $({\lambda }_c=0,\mu =0)$.

It can be shown that

$$\begin{array}{cc}\hfill {\left.\frac{\partial C_{FT}^x}{\partial {\lambda }_c}\right|}_{{\lambda }_c=0,\mu =0}& =\frac{1}{8}{c}_{l,\alpha }(\delta -1)\sigma \left(4+\frac{4c_{l,\alpha }(\delta -1)\sigma }{\sqrt{(\delta -1)\sigma (-8c_{l,0}(1+\delta )+c_{l,\alpha }(c_{l,\alpha }(\delta -1)\sigma -16{\theta }_{\mathrm{tip}}))}}\right)\hfill \end{array}$$

(90)

$$\begin{array}{cc}\hfill {\left.\frac{\partial C_{FT}^x}{\partial \mu }\right|}_{{\lambda }_c=0,\mu =0}& =0\hfill \end{array}$$

(91)

$$\begin{array}{cc}\hfill {\left.\frac{{\partial }^2{C}_{FT}^x}{\partial {\lambda }_c^2}\right|}_{{\lambda }_c=0,\mu =0}& =-\frac{16c_{l,\alpha }{(\delta -1)}^2{\sigma }^2(c_{l,0}+c_{l,0}\delta +2c_{l,\alpha }{\theta }_{\mathrm{tip}})}{{((\delta -1)\sigma (-8c_{l,0}(1+\delta )+c_{l,\alpha }(c_{l,\alpha }(\delta -1)\sigma -16{\theta }_{\mathrm{tip}})))}^{3/2}}\hfill \end{array}$$

(92)

$$\begin{array}{cc}\hfill {\left.\frac{{\partial }^2{C}_{FT}^x}{\partial {\lambda }_c\partial \mu }\right|}_{{\lambda }_c=0,\mu =0}& =0\hfill \end{array}$$

(93)

$$\begin{array}{cc}\hfill {\left.\frac{{\partial }^2{C}_{FT}^x}{\partial {\mu }^2}\right|}_{{\lambda }_c=0,\mu =0}& =-c_{l,0}\sigma ln(\delta )-\frac{c_{l,\alpha }(\delta -1)\sigma \left({\theta }_{\mathrm{tip}}+\frac{\sigma (c_{l,\alpha }(\delta -1){\theta }_{\mathrm{tip}}+c_{l,0}\delta ln(\delta )}{\sqrt{(\delta -1)\sigma (-8c_{l,0}(1+\delta )+c_{l,\alpha }(c_{l,\alpha }(\delta -1)\sigma -16{\theta }_{\mathrm{tip}}))}}\right)}{\delta }\hfill \end{array}$$

(94)

Thus,

$$\begin{array}{c}\hfill C_{FT}^{2\mathrm{nd}}({\lambda }_c,\mu )=C_{FT}^{\mathrm{static}}+k_1{\lambda }_c+k_2{\mu }^2+k_3{\lambda }_c^2\end{array}$$

(95)

where

$$\begin{array}{cc}\hfill k_1& :={\left.\frac{\partial C_{FT}^x}{\partial \mu }\right|}_{{\lambda }_c=0,\mu =0}\hfill \end{array}$$

(96)

$$\begin{array}{cc}\hfill k_2& :=\frac{1}{2}{\left.\frac{{\partial }^2{C}_{FT}^x}{\partial {\mu }^2}\right|}_{{\lambda }_c=0,\mu =0}\hfill \end{array}$$

(97)

$$\begin{array}{cc}\hfill k_3& :=\frac{1}{2}{\left.\frac{{\partial }^2{C}_{FT}^x}{\partial {\mu }^2}\right|}_{{\lambda }_c=0,\mu =0}\hfill \end{array}$$

(98)

However, one can view the $k_i$’s as lumped parameters over which a parameter fitting procedure can be carried out (or evaluated using the parameter generation given the static coefficients as explained in Section 4), similar to the approach outlined in Section 3. This will be done in practice in Section 5.2, and since the second-order model is linear in the new parameters $k_i$, the fitting problem becomes convex and CVXPY [81,82] is used to yield the optimal parameter vector $k^{*}$.

Performing the same second-order Taylor series expansion on the remaining coefficients yield

$$\begin{array}{cc}\hfill C_{FH}^{2\mathrm{nd}}({\lambda }_c,\mu )& =k_4\mu +k_5{\lambda }_c\mu \hfill \end{array}$$

(99)

$$\begin{array}{cc}\hfill C_{MQ}^{2\mathrm{nd}}({\lambda }_c,\mu )& =C_{MQ}^{\mathrm{static}}+k_6{\lambda }_c+k_7{\mu }^2+k_8{\lambda }_c^2\hfill \end{array}$$

(100)

$$\begin{array}{cc}\hfill C_{MR}^{2\mathrm{nd}}({\lambda }_c,\mu )& =k_9\mu +k_{10}{\lambda }_c\mu \hfill \end{array}$$

(101)

$$\begin{array}{cc}\hfill C_{MP}^{2\mathrm{nd}}({\lambda }_c,\mu )& =k_{11}\mu +k_{12}{\lambda }_c\mu \hfill \end{array}$$

(102)

where the corresponding partial derivatives are evaluated in Appendix B. Note that the model now contains 14 total parameters to identify (including the hover thrust and torque coefficients). Note that a black-box second-order multinomial for (1) would contain $5(1+3+6)=50$ parameters.

5.2. Experimental Assessment

5.2.1. Oblique Flow Results

The models can be viewed for one of the propellers in Figure 16 and Figure 17 (the plots for the remaining tested propellers are available in Supplementary Dataset S1), and Figure 18 shows the errors for the oblique flow datasets. A few observations can be made:

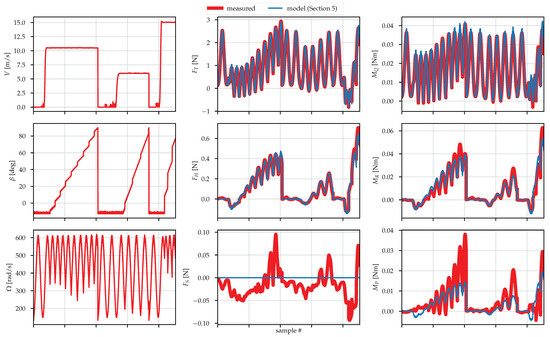
Figure 16. Propeller: mamr-8x4.5. Note that the points corresponding to ${\lambda }_c<0$, ${\lambda }_c>0.3$ and $\mu >0.3$ have been thrown away, as mentioned in Section 3.2. Note that (1) neglects the side force $F_S$, so the model is set to output $0[\mathrm{N}]$. Model is as per Section 5.

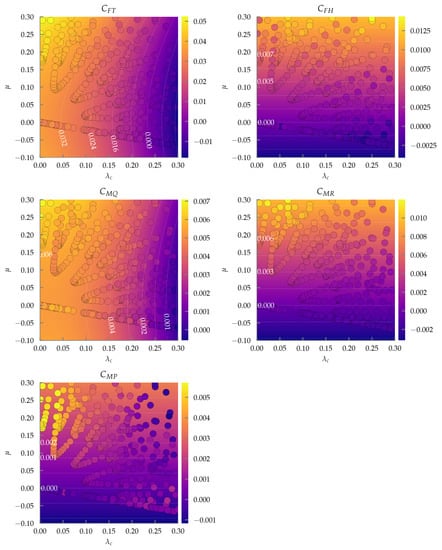
Figure 17. Propeller: mamr-8x4.5, in the dimensionless space. Measured data are shown as circles, and the fitted model as described in Section 5 is depicted as a contour plot with associated labelled contour lines.

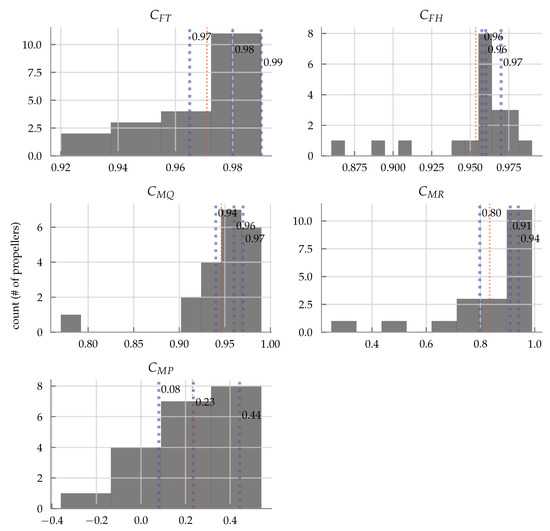
Figure 18. Histogram of $R^2$ values for each force and moment coefficient using the fitted model as described in Section 5 for all 20 propellers tested under oblique flow. The errors along with the parameter values can be found in tabular format in Table A5 in Appendix A. The blue dotted lines represent the 25, 50, and 75th percentiles and are labelled, and the red dotted line represents the mean.

• The models for thrust, H-force, rotor torque, and rolling moments all perform very well, even over the entirety of the tested domain (${\lambda }_c\le 0.3$, $\mu \le 0.3$), with median $R^2$ values above 0.91. However, the model for the pitching moment does not, which implies that the domain over which the second-order Taylor expansion for the pitching moment is valid is far smaller than the rest of the models, as can be seen in Figure 17.
• From the parameter values in Table A5 in Appendix A, the parameters $k_5\approx 0$ and $k_{10}\approx 0$, so these may potentially be ignored in a practical implementation.

5.2.2. Axial Flow Results

Figure 19 shows the errors for the axial flow dataset [68]. The model fitting is near perfect in this case.

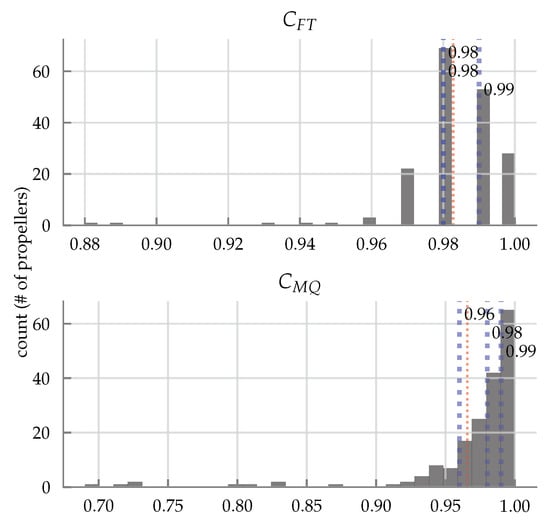
Figure 19. Histogram of $R^2$ values for each force and moment coefficient using the fitted model as described in Section 5 for the 180 propellers tested under axial flow from the dataset [68]. The errors along with the parameter values can be found in tabular format in Table A6 in Appendix A. The blue dotted lines represent the 25, 50, and 75th percentiles and are labelled, and the red dotted line represents the mean.

6. Conclusion and Future Work

Two analytical, parametric models have been developed for (1), with various parameter generation methods corresponding to Section 2, Section 3, Section 4 and Section 5. An oblique flow dataset has also been collected for 19 UAV propellers. Because of the analytical nature, the models are simple to implement and fast to compute, suitable for real-time applications.

The accuracy of the first model is very high for all loads when trained using labelled data in a grey-box identification approach, as shown in Section 3. When no labelled data is available, and the parameter values already determined in Table A1 in Appendix A cannot be used, then one could elect to use the method outlined in Section 4 which only relies on the static thrust and torque coefficients, thereby providing good prediction of the loads in the full forward flight regime. The second-order Taylor series model of Section 5 also results in very accurate models, except for the pitching moment.

A simpler model for the pitching moment could be a suitable direction for future work. Another direction could be to look at micro UAV propellers specifically, which typically use a constant chord model, and to apply the methodology of Section 4 to see if the accuracy of the predicted model can be improved. Further directions in modelling include looking into the windmill-brake operating regime [34] (${\lambda }_c<0$). Another direction is to utilize the proposed models herein for real-time estimation, control, and simulation purposes.