Biologically-Inspired Intelligent Flocking Control for Networked Multi-UAS with Uncertain Network Imperfections
Abstract
1. Introduction
1.1. Motivation
1.2. Related Works
1.3. Main Contributions
- The knowledge of system dynamics is not fully or partially required.
- It has the capabilities of overcoming the network-induced delay, handling the uncertainties, and noise/disturbance rejection.
- It is appropriate for real-time implementation due to its low computational complexity (i.e., the developed algorithm is a real-time applicable learning technique).
- It ensures the stability of the system.
2. Problem Formulation and Preliminaries
2.1. Flock Modelling
- (i).
- is the interaction component between two -agents and is defined as follows:where and are positive constants. The terms and are vector and the elements of the spatial adjacency matrix , respectively, which are described as follows:where , and for all i and q.
- (ii).
- is the interaction component between the -agent and an obstacle (named the -agent) and is defined as follows:where and are positive constants. and are position, and velocity of the kth obstacle (i.e., -agent), respectively. The terms and are vector and the elements of the heterogeneous adjacency matrix , respectively, which are defined as follows:is a repulsive action function and is the set of -neighbors of an -agent i, where the range of interaction of an -agent with obstacles is the positive constant . Here, , and
- (iii).
- is a goal component that consists of a distributed navigational feedback term and is defined as follows:where and are positive constants.
2.2. Network-Induced Delays
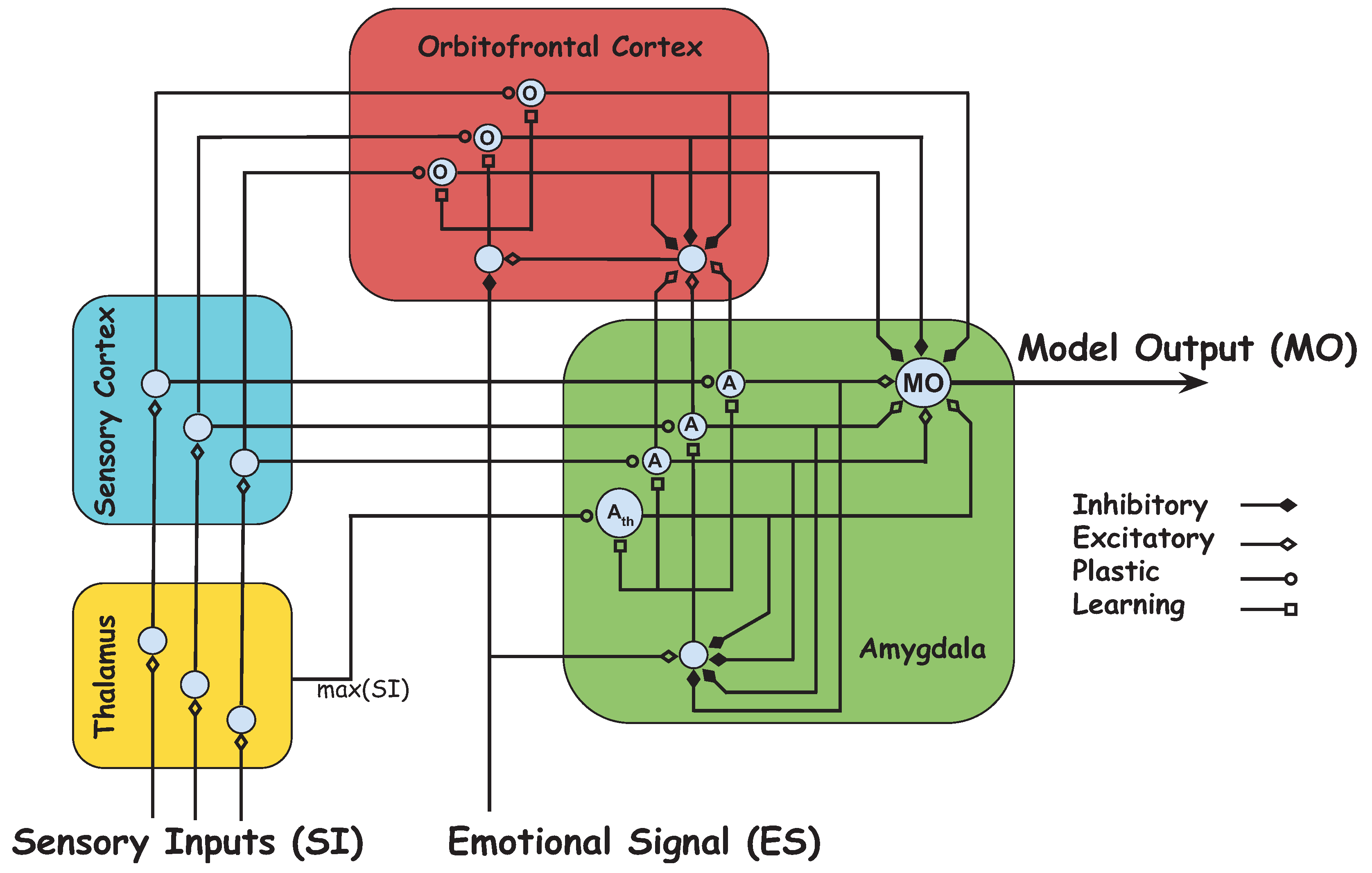
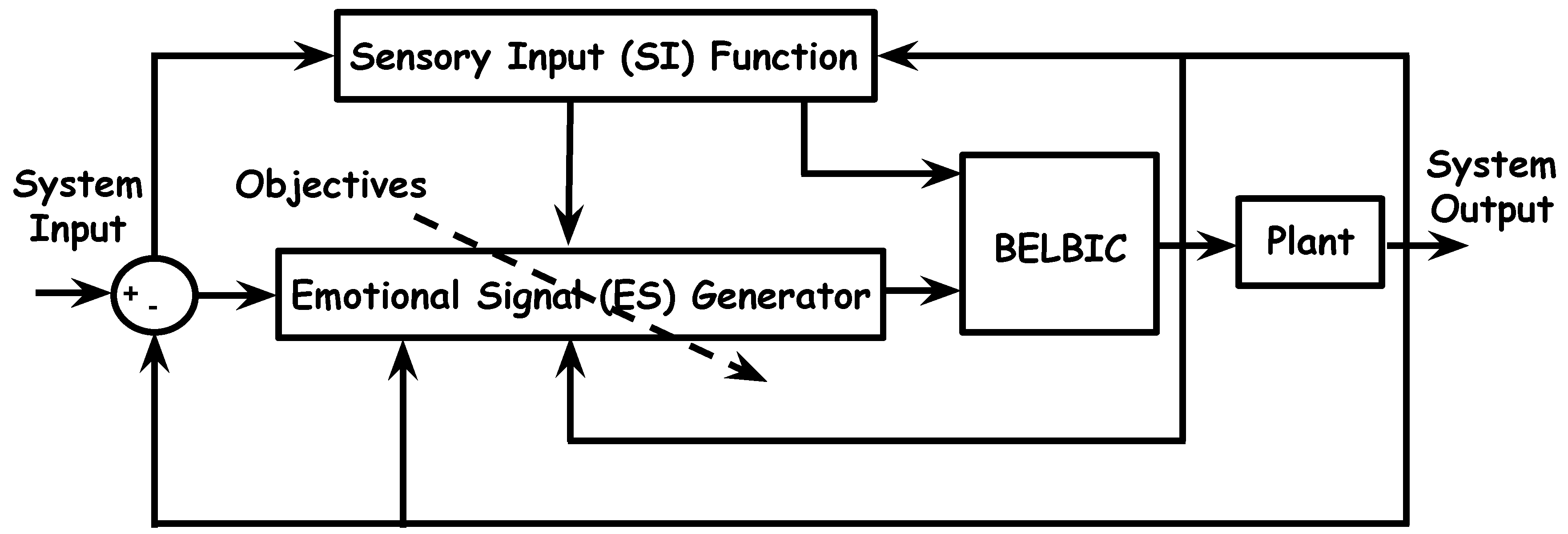
2.3. Brain Emotional Learning-Based Intelligent Controller
2.4. Objectives
3. Distributed Intelligent Flocking Control of Networked Multi-UAS Using Emotional Learning
3.1. System Design
3.2. Emotional Signal and Sensory Input Development
3.3. Learning-Based Intelligent Flocking Control
| Algorithm 1 : The BELBIC-inspired methodology for distributed intelligent flocking control of networked multi-UAS. |
| Initialization: |
| Set , , and , for . |
| Define network-induced delay. |
| Define Objective function, for . |
| for each iteration do |
| for each agent i do |
| Compute |
| Compute |
| Compute |
| Compute |
| Compute |
| Compute |
| Update |
| Update |
| Update |
| end for |
| end for |
3.4. Stability Analysis
- I.
- II.
4. Simulation Results
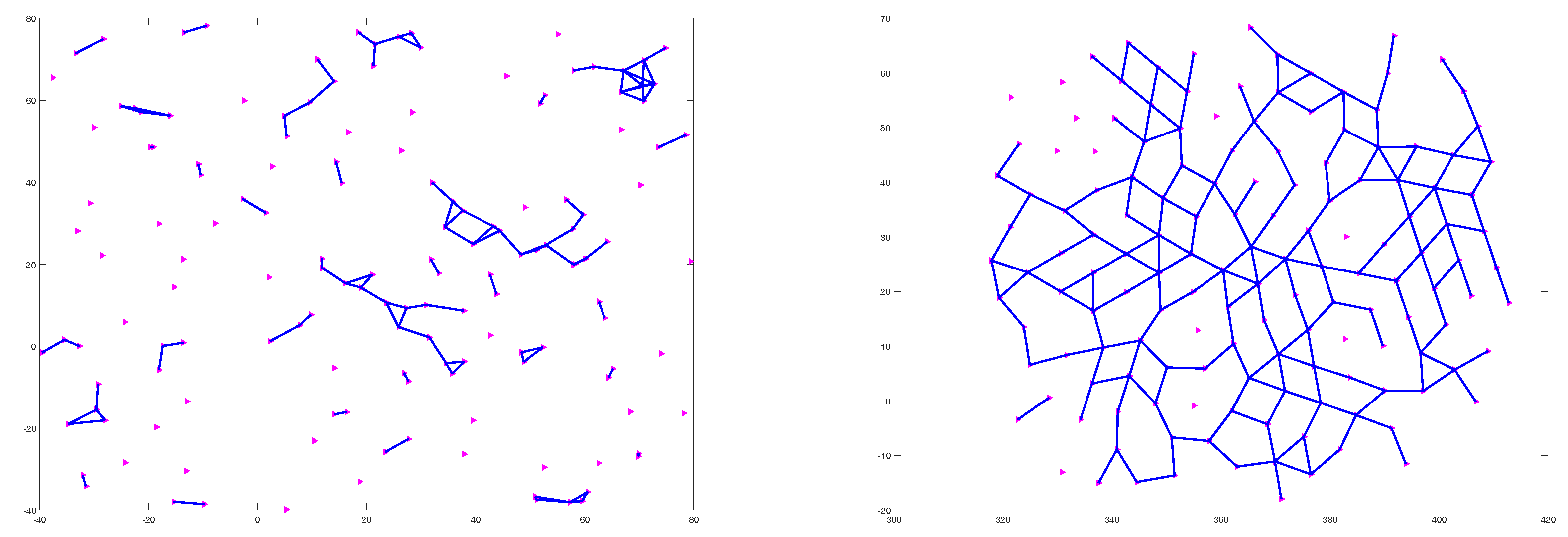
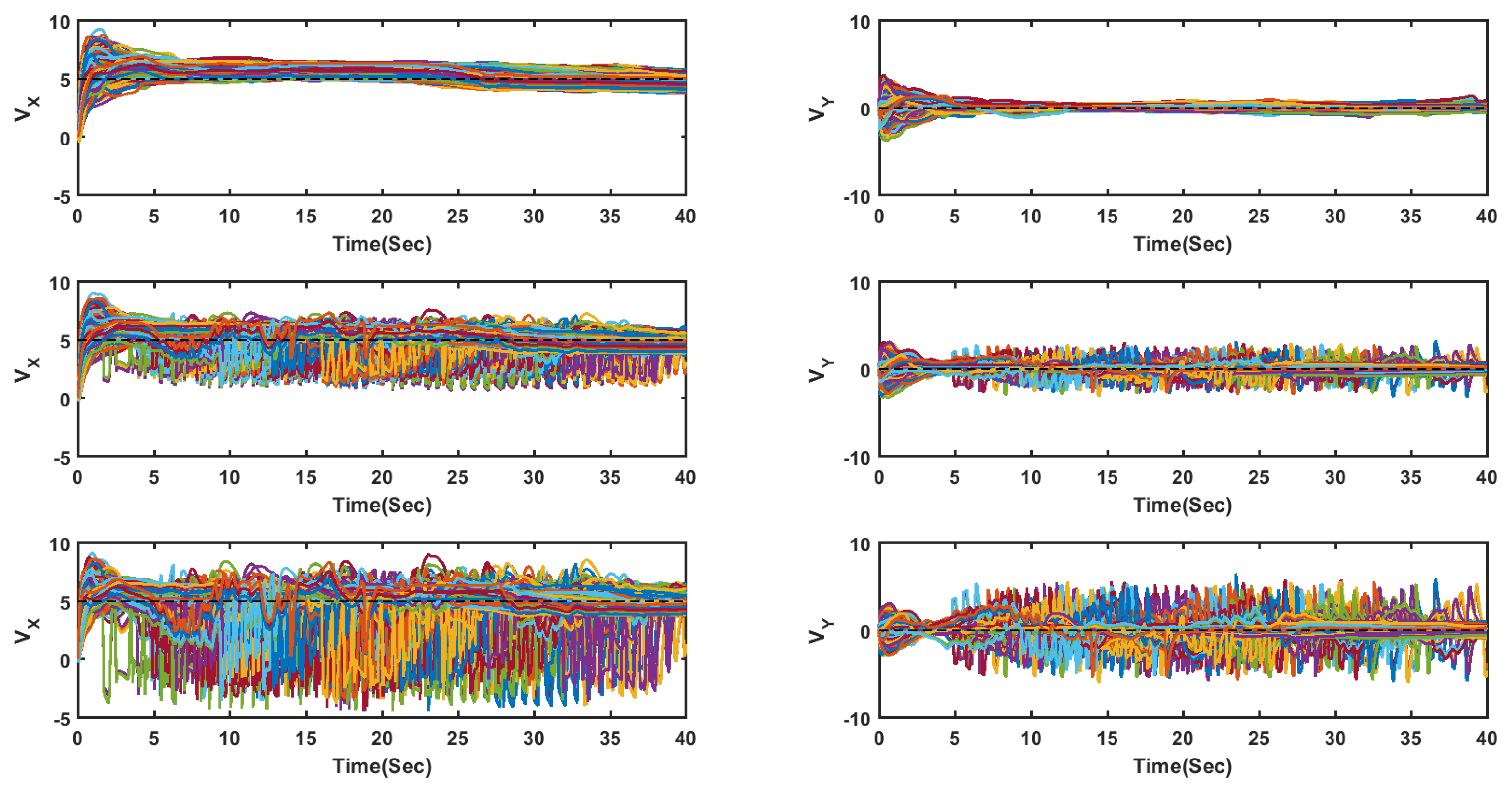
4.1. Flocking of UGVs in an Obstacle-Free Environment
4.2. Flocking of UASs in an Obstacle-Free Environment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A.
Appendix A.1. Non-Adapting Phase
Appendix A.2. Main Proof
- I.
- II.
Appendix B.
References
- Reynolds, C.W. Flocks, herds and schools: A distributed behavioral model. ACM SIGGRAPH Comput. Graph. 1987, 21, 25–34. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Murray, R.M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Olfati-Saber, R. Flocking for multi-agent dynamic systems: Algorithms and theory. IEEE Trans. Autom. Control 2006, 51, 401–420. [Google Scholar] [CrossRef]
- Liu, B.; Yu, H. Flocking in multi-agent systems with a bounded control input. In Proceedings of the 2009 IWCFTA’09. International Workshop on IEEE Chaos-Fractals Theories and Applications, Los Alamitos, CA, USA, 6–8 November 2009; pp. 130–134. [Google Scholar]
- Jafari, M. On the Cooperative Control and Obstacle Avoidance of Multi-Vehicle Systems. Master’s Thesis, University of Nevada, Reno, NV, USA, 2015. [Google Scholar]
- Xu, H.; Carrillo, L.R.G. Distributed near optimal flocking control for multiple Unmanned Aircraft Systems. In Proceedings of the IEEE 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 879–885. [Google Scholar]
- Jafari, M.; Sengupta, S.; La, H.M. Adaptive flocking control of multiple unmanned ground vehicles by using a uav. In Proceedings of the International Symposium on Visual Computing, Las Vegas, NV, USA, 14–16 December 2015; pp. 628–637. [Google Scholar]
- O’Loan, O.; Evans, M. Alternating steady state in one-dimensional flocking. J. Phys. A Math. Gen. 1999, 32, L99. [Google Scholar] [CrossRef]
- Li, S.; Liu, X.; Tang, W.; Zhang, J. Flocking of Multi-Agents Following a Leader with Adaptive Protocol in a Noisy Environment. Asian J. Control 2014, 16, 1771–1778. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, P.; Yang, Z.; Chen, Z. Adaptive flocking of non-linear multi-agents systems with uncertain parameters. IET Control Theory Appl. 2014, 9, 351–357. [Google Scholar] [CrossRef]
- Dong, Y.; Huang, J. Flocking with connectivity preservation of multiple double integrator systems subject to external disturbances by a distributed control law. Automatica 2015, 55, 197–203. [Google Scholar] [CrossRef]
- Jafari, M.; Xu, H.; Carrillo, L.R.G. Brain Emotional Learning-Based Intelligent Controller for flocking of Multi-Agent Systems. In Proceedings of the 2017 IEEE American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 1996–2001. [Google Scholar]
- Chopra, N.; Spong, M.W. Output synchronization of nonlinear systems with time delay in communication. In Proceedings of the 2006 45th IEEE Conference on IEEE, Decision and Control, Sydney, Australia, 13–15 December 2006; pp. 4986–4992. [Google Scholar]
- Nourmohammadi, A.; Jafari, M.; Zander, T.O. A Survey on Unmanned Aerial Vehicle Remote Control Using Brain–Computer Interface. IEEE Trans. Hum. Mach. Syst. 2018, 48, 337–348. [Google Scholar] [CrossRef]
- Wan, Z. Flocking for Multi-Agent Dynamical Systems. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2012. [Google Scholar]
- Yang, Z.; Zhang, Q.; Jiang, Z.; Chen, Z. Flocking of multi-agents with time delay. Int. J. Syst. Sci. 2012, 43, 2125–2134. [Google Scholar] [CrossRef]
- Liu, Y.; Ho, D.W.; Wang, Z. A new framework for consensus for discrete-time directed networks of multi-agents with distributed delays. Int. J. Control 2012, 85, 1755–1765. [Google Scholar] [CrossRef]
- Kar, S.; Moura, J.M. Distributed consensus algorithms in sensor networks with imperfect communication: Link failures and channel noise. IEEE Trans. Signal Process. 2009, 57, 355–369. [Google Scholar] [CrossRef]
- Mehrabian, A.R.; Khorasani, K. Distributed formation recovery control of heterogeneous multiagent euler–lagrange systems subject to network switching and diagnostic imperfections. IEEE Trans. Control Syst. Technol. 2016, 24, 2158–2166. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, P.; Yang, Z.; Chen, Z. Distance constrained based adaptive flocking control for multiagent networks with time delay. Math. Probl. Eng. 2015, 2015. [Google Scholar] [CrossRef]
- Cao, Y.; Oguchi, T. Coordinated Control of Mobile Robots with Delay Compensation Based on Synchronization. In Sensing and Control for Autonomous Vehicles; Springer: Berlin, Germany, 2017; pp. 495–514. [Google Scholar]
- Dashti, Z.A.S.; Gholami, M.; Jafari, M.; Shoorehdeli, M.A.; Teshnehlab, M. Speed control of a Digital Servo System using parallel distributed compensation controller and Neural Adaptive controller. In Proceedings of the 2013 13th Iranian Conference on IEEE, Fuzzy Systems (IFSC), Qazvin, Iran, 27–29 August 2013; pp. 1–6. [Google Scholar]
- Jafari, M.; Xu, H.; Garcia Carrillo, L.R. A neurobiologically-inspired intelligent trajectory tracking control for unmanned aircraft systems with uncertain system dynamics and disturbance. Trans. Inst. Meas. Control 2018. [Google Scholar] [CrossRef]
- Jafari, M.; Sarfi, V.; Ghasemkhani, A.; Livani, H.; Yang, L.; Xu, H.; Koosha, R. Adaptive neural network based intelligent secondary control for microgrids. In Proceedings of the 2018 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 8–9 February 2018; pp. 1–6. [Google Scholar]
- Moren, J.; Balkenius, C. A computational model of emotional learning in the amygdala. Anim. Anim. 2000, 6, 115–124. [Google Scholar]
- Lucas, C.; Shahmirzadi, D.; Sheikholeslami, N. Introducing BELBIC: brain emotional learning based intelligent controller. Intell. Autom. Soft Comput. 2004, 10, 11–21. [Google Scholar] [CrossRef]
- Kim, J.W.; Oh, C.Y.; Chung, J.W.; Kim, K.H. Brain emotional limbic-based intelligent controller design for control of a haptic device. Int. J. Autom. Control 2017, 11, 358–371. [Google Scholar] [CrossRef]
- Rizzi, C.; Johnson, C.G.; Fabris, F.; Vargas, P.A. A situation-aware fear learning (SAFEL) model for robots. Neurocomputing 2017, 221, 32–47. [Google Scholar] [CrossRef]
- Jafari, M.; Xu, H. A Biologically-Inspired Distributed Intelligent Flocking Control for Networked Multi-UAS with Uncertain Network Imperfections. In Proceedings of the 2018 International Conference on Unmanned Aircraft Systems (ICUAS), Dallas, TX, USA, 12–15 June 2018; pp. 12–21. [Google Scholar]
- Jafari, M.; Xu, H. Intelligent Control for Unmanned Aerial Systems with System Uncertainties and Disturbances Using Artificial Neural Network. Drones 2018, 2, 30. [Google Scholar] [CrossRef]
- Jafari, M.; Shahri, A.M.; Shouraki, S.B. Attitude control of a quadrotor using brain emotional learning based intelligent controller. In Proceedings of the 2013 13th Iranian Conference on IEEE, Fuzzy Systems (IFSC), Qazvin, Iran, 27–29 August 2013; pp. 1–5. [Google Scholar]
- Jafari, M.; Shahri, A.M.; Elyas, S.H. Optimal Tuning of Brain Emotional Learning Based Intelligent Controller Using Clonal Selection Algorithm. In Proceedings of the 2013 3th International eConference on IEEE, Computer and Knowledge Engineering (ICCKE), Mashhad, Iran, 31 October–1 November 2013; pp. 30–34. [Google Scholar]
- Lin, C.M.; Chung, C.C. Fuzzy Brain Emotional Learning Control System Design for Nonlinear Systems. Int. J. Fuzzy Syst. 2015, 17, 117–128. [Google Scholar] [CrossRef]
- Mei, Y.; Tan, G.; Liu, Z. An improved brain-inspired emotional learning algorithm for fast classification. Algorithms 2017, 10, 70. [Google Scholar] [CrossRef]
- El-Garhy, M.A.A.A.; Mubarak, R.; El-Bably, M. Improving maximum power point tracking of partially shaded photovoltaic system by using IPSO-BELBIC. J. Instrum. 2017, 12, P08012. [Google Scholar] [CrossRef]
- La, H.M.; Lim, R.; Sheng, W. Multirobot cooperative learning for predator avoidance. IEEE Trans. Control Syst. Technol. 2015, 23, 52–63. [Google Scholar] [CrossRef]
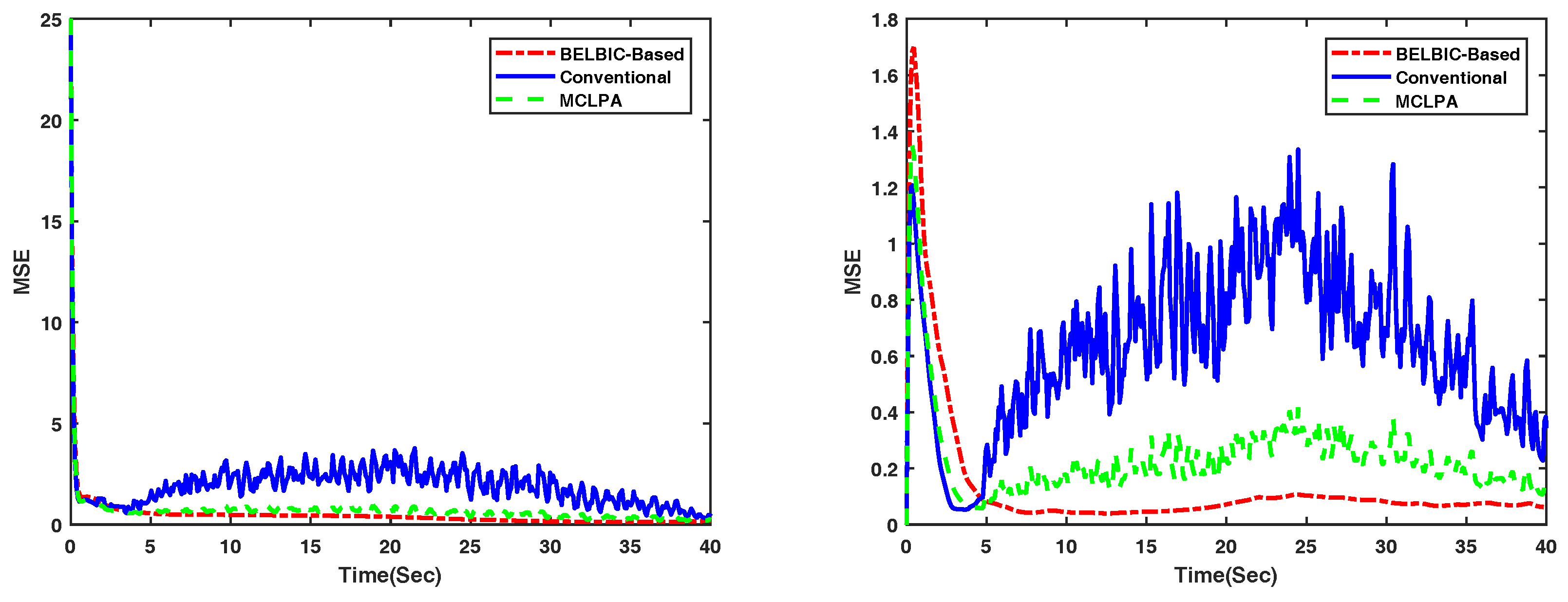
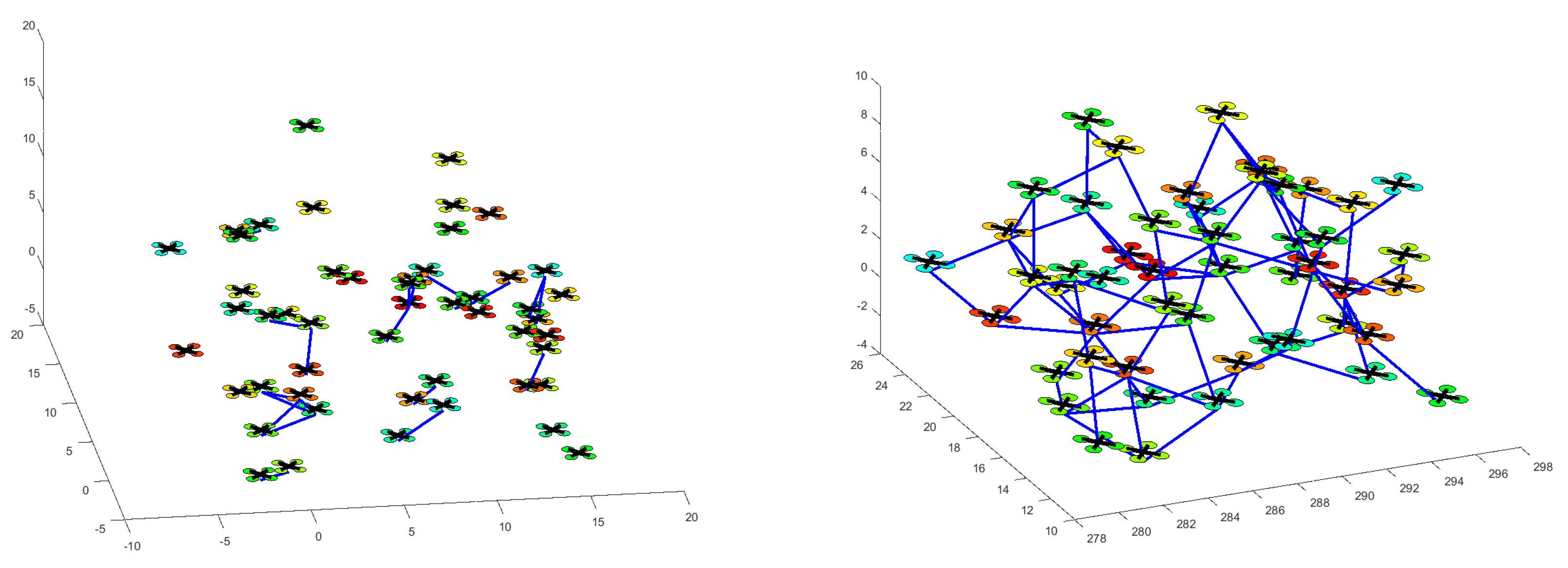
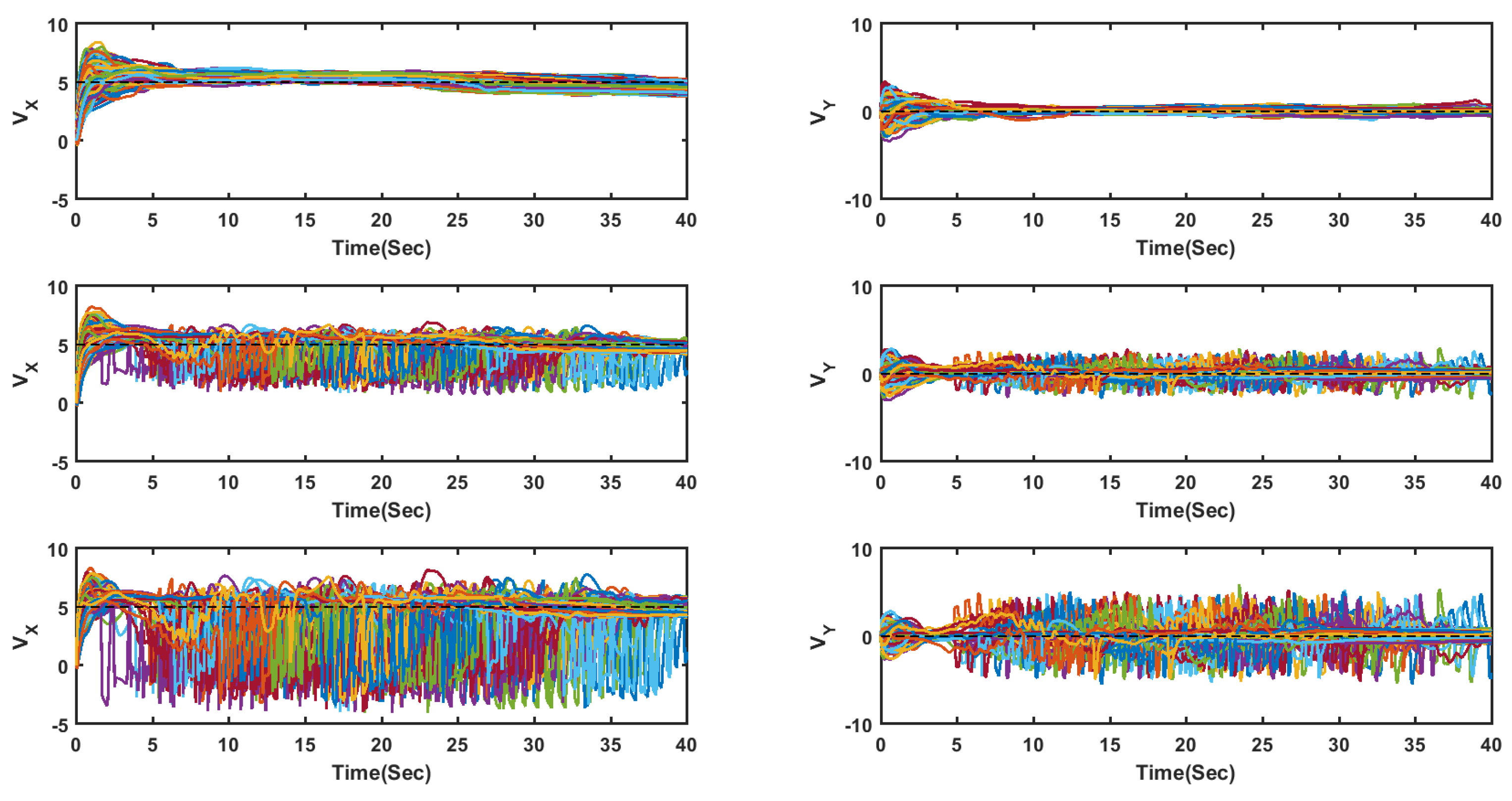
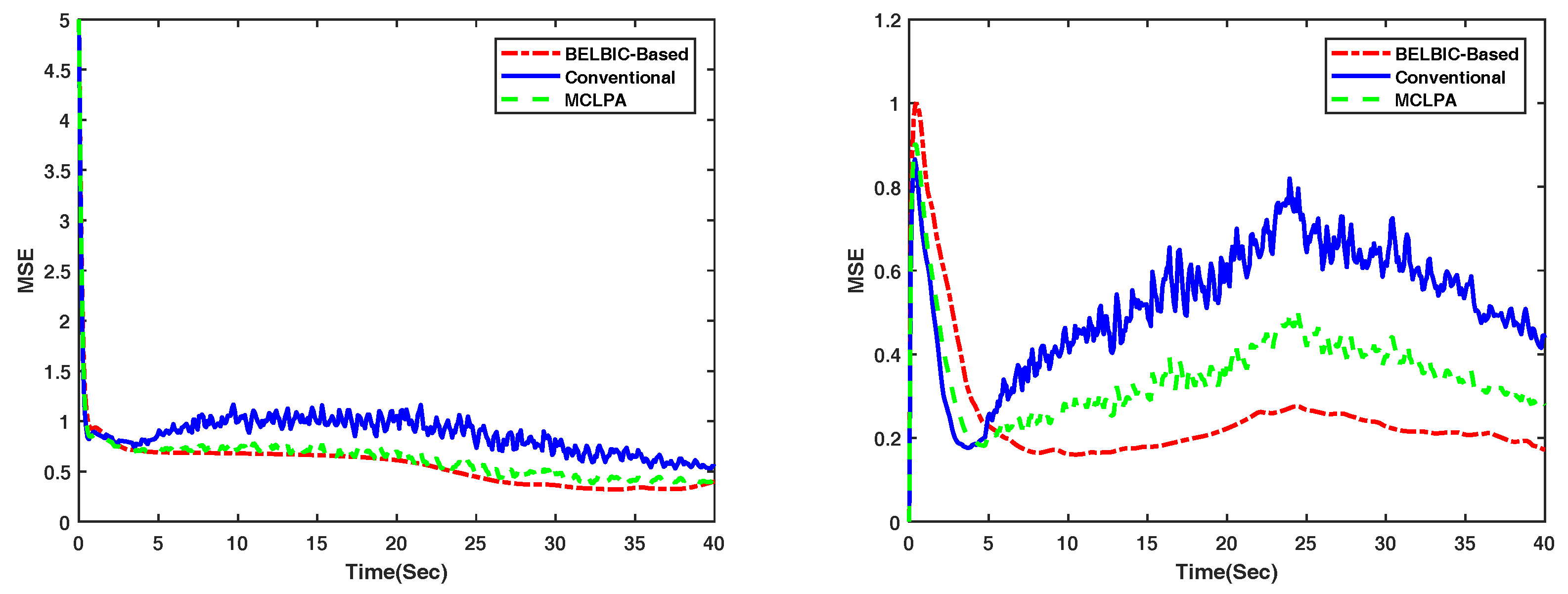
| Flocking in [3] | MCLPA [36] | BELBIC-Based | |
|---|---|---|---|
| Mean Value on the x-axis | 0.802 | 0.641 | 0.602 |
| Standard Deviation on the x-axis | 6.025 × 10−5 | 5.566 × 10−5 | 0.814 × 10−5 |
| Mean Value on the y-axis | 0.371 | 0.245 | 0.176 |
| Standard Deviation on the y-axis | 6.869 × 10−4 | 3.068 × 10−4 | 1.324 × 10−4 |
| Flocking in [3] | MCLPA [36] | BELBIC-Based | |
|---|---|---|---|
| Mean Value on the x-axis | 0.762 | 0.581 | 0.512 |
| Standard Deviation on the x-axis | 5.726 × 10−5 | 5.065 × 10−5 | 0.764 × 10−5 |
| Mean Value on the y-axis | 0.356 | 0.225 | 0.147 |
| Standard Deviation on the y-axis | 6.439 × 10−4 | 2.805 × 10−4 | 1.042 × 10−4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jafari, M.; Xu, H. Biologically-Inspired Intelligent Flocking Control for Networked Multi-UAS with Uncertain Network Imperfections. Drones 2018, 2, 33. https://doi.org/10.3390/drones2040033
Jafari M, Xu H. Biologically-Inspired Intelligent Flocking Control for Networked Multi-UAS with Uncertain Network Imperfections. Drones. 2018; 2(4):33. https://doi.org/10.3390/drones2040033
Chicago/Turabian StyleJafari, Mohammad, and Hao Xu. 2018. "Biologically-Inspired Intelligent Flocking Control for Networked Multi-UAS with Uncertain Network Imperfections" Drones 2, no. 4: 33. https://doi.org/10.3390/drones2040033
APA StyleJafari, M., & Xu, H. (2018). Biologically-Inspired Intelligent Flocking Control for Networked Multi-UAS with Uncertain Network Imperfections. Drones, 2(4), 33. https://doi.org/10.3390/drones2040033






