Shipborne Stabilization Grasping Low-Altitude Drones Method for UAV-Assisted Landing Dock Stations
Highlights
- Present the manipulator arm designed for charging shipborne drones that utilize low-altitude visual servo grasp-docking.
- Present a global Jacobian matrix which covers not only the six degree-of-freedom (DOF) of the manipulator arm, but also the nonholonomic shipborne base.
- Provide a long-endurance way to drones charging and recover on water surface.
- Provide a flow field disturbance stabilization for drones landing on water surface.
Abstract
1. Introduction
2. Global Jacobian Matrix and Global Dynamic Model
2.1. Global Jacobian Matrix and Kinematics of the Shipborne Grasping Arm
2.2. Global Dynamics of the Shipborne Grasping Arm
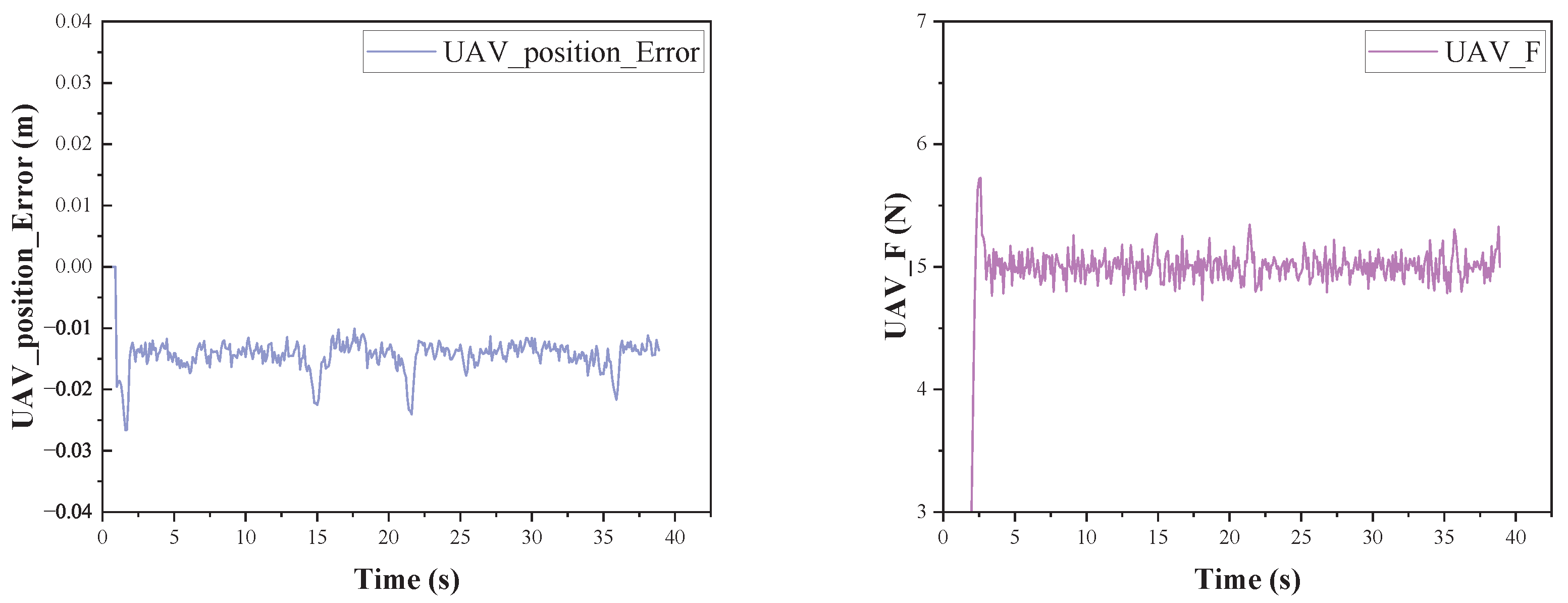
3. Proposed Grasp Docking Paradigm and Experimental Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Riboldi, C.E.D.; Fanchini, L. Assessing the Technical–Economic Feasibility of Low-Altitude Unmanned Airships: Methodology and Comparative Case Studies. Aerospace 2025, 12, 244. [Google Scholar] [CrossRef]
- Thomas, J.; Loianno, G.; Daniilidis, K.; Kumar, V. Visual Servoing of Quadrotors for Perching by Hanging From Cylindrical Objects. IEEE Robot. Autom. Lett. 2016, 1, 57–64. [Google Scholar] [CrossRef]
- Hang, K.; Lyu, X.; Song, H.; Stork, J.A.; Dollar, A.M.; Kragic, D.; Zhang, F. Perching and resting—A paradigm for UAV maneuvering with modularized landing gears. Sci. Robot. 2019, 4, 6637–6645. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.; Wang, D.; Yuan, T.; Zhang, J.; Liu, G.; Li, X.; Chen, X.; Wang, C.; Cai, S.; et al. Electrically active smart adhesive for a perching-and-takeoff robot. Sci. Adv. 2023, 9, 3133–3145. [Google Scholar] [CrossRef]
- Kremer, P.; Nohooji, H.R.; Voos, H. Constrained Trajectory Optimization and Force Control for UAVs with Universal Jamming Grippers. Res. Sq. 2023. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Li, H.; Ai, J. Runway-Free Recovery Methods for Fixed-Wing UAVs: A Comprehensive Review. Drones 2024, 8, 463. [Google Scholar] [CrossRef]
- Cho, G.; Choi, J.; Bae, G.; Oh, H. Autonomous ship deck landing of a quadrotor UAV using feed-forward image-based visual servoing. Aerosp. Sci. Technol. 2022, 130, 107869. [Google Scholar] [CrossRef]
- Yang, T.; Ren, Q.; Zhang, F.; Xie, B.; Ren, H.; Li, J.; Zhang, Y. Hybrid Camera Array-Based UAV Auto-Landing on Moving UGV in GPS-Denied Environment. Remote Sens. 2018, 10, 1829. [Google Scholar] [CrossRef]
- Lippiello, V.; Mebarki, R.; Ruggiero, F. Visual coordinated landing of a UAV on a mobile robot manipulator. In Proceedings of the 2013 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Linköping, Sweden, 21–26 October 2013; pp. 1–7. [Google Scholar] [CrossRef]
- Falanga, D.; Zanchettin, A.; Simovic, A.; Delmerico, J.; Scaramuzza, D. Vision-based autonomous quadrotor landing on a moving platform. In Proceedings of the 2017 IEEE International Symposium on Safety, Security and Rescue Robotics (SSRR), Shanghai, China, 11–13 October 2017; pp. 200–207. [Google Scholar] [CrossRef]
- Xie, J.; Peng, X.; Wang, H.; Niu, W.; Zheng, X. UAV autonomous tracking and landing based on deep reinforcement learning strategy. Sensors 2020, 20, 5630. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Zhang, L.; Li, X.; Wang, H.; Gao, B. Grasping Low-Altitude Drones Technology for Shipborne UAV Charging Stations. In Proceedings of the 2025 IEEE 15th International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Shanghai, China, 15–18 July 2025; pp. 202–205. [Google Scholar] [CrossRef]
- Grlj, C.G.; Krznar, N.; Pranjić, M. A Decade of UAV Docking Stations: A Brief Overview of Mobile and Fixed Landing Platforms. Drones 2022, 6, 17. [Google Scholar] [CrossRef]
- Shao, G.; Ma, Y.; Malekian, R.; Yan, X.; Li, Z. A novel cooperative platform design for coupled USV–UAV systems. IEEE Trans. Ind. Inform. 2019, 15, 4913–4922. [Google Scholar] [CrossRef]
- Kyriakakis, N.A.; Stamadianos, T.; Marinaki, M.; Marinakis, Y. The electric vehicle routing problem with drones: An energy minimization approach for aerial deliveries. Clean. Logist. Supply Chain 2022, 4, 100041. [Google Scholar] [CrossRef]
- Pachayappan, M.; Sudhakar, V. A Solution to Drone Routing Problems using Docking Stations for Pickup and Delivery Services. Transp. Res. Rec. 2021, 2675, 1056–1074. [Google Scholar] [CrossRef]
- Su, Z.; Liu, Y.; Wang, H. Probe Dynamics Direct Control for Aerial Recovery with Preassigned Docking Performance. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3509–3523. [Google Scholar] [CrossRef]
- Dong, H.; Wu, Z.; Wang, J.; Chen, D.; Tan, M.; Yu, J. Implementation of Autonomous Docking and Charging for a Supporting Robotic Fish. IEEE Trans. Ind. Electron. 2023, 70, 7023–7031. [Google Scholar] [CrossRef]
- Page, B.R.; Mahmoudian, N. Simulation-Driven Optimization of Underwater Docking Station Design. IEEE J. Ocean. Eng. 2020, 45, 404–413. [Google Scholar] [CrossRef]
- Teo, K.; Goh, B.; Chai, O.K. Fuzzy Docking Guidance Using Augmented Navigation System on an UAV. IEEE J. Ocean. Eng. 2015, 40, 349–361. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Q.; Zhao, D.; Wang, L.; Jia, T. Electrical Aircraft Ship Integrated Secure and Traverse System Design and Key Characteristics Analysis. Appl. Sci. 2022, 12, 2603. [Google Scholar] [CrossRef]
- Welschehold, T.; Dornhege, C.; Paus, F.; Asfour, T.; Burgard, W. Coupling mobile base and end-effector motion in task space. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Madrid, Spain, 1–5 October 2018; pp. 7158–7163. [Google Scholar]
- Aissi, M.; Moumen, Y.; Berrich, J.; Bouchentouf, T.; Bourhaleb, M.; Rahmoun, M. Autonomous solar USV with an automated launch and recovery system for UAV: State of the art and Design. In Proceedings of the 2020 IEEE 2nd International Conference on Electronics, Control, Optimization and Computer Science (ICECOCS), Kenitra, Morocco, 2–3 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Sanchez-Lopez, J.L.; Pestana, J.; Saripalli, S.; Campoy, P. An approach toward visual autonomous ship board landing of a VTOL UAV. J. Intell. Robot. Syst. 2014, 74, 113–127. [Google Scholar] [CrossRef]
- Morando, A.E.S.; Bozzi, A.; Graffione, S.; Sacile, R.; Zero, E. Optimizing Unmanned Air–Ground Vehicle Maneuvers Using Nonlinear Model Predictive Control and Moving Horizon Estimation. Automation 2024, 5, 324–342. [Google Scholar] [CrossRef]
- Delbene, A.; Baglietto, M.; Simetti, E. Visual Servoed Autonomous Landing of an UAV on a Catamaran in a Marine Environment. Sensors 2022, 22, 3544. [Google Scholar] [CrossRef] [PubMed]
- Er, M.J.; Gao, W.; Li, Q.; Li, L.; Liu, T. Composite trajectory tracking of a ship-borne manipulator system based on full-order terminal sliding mode control under external disturbances and model uncertainties. Ocean Eng. 2023, 267, 113203. [Google Scholar] [CrossRef]
- Xia, K.; Son, H. Adaptive fixed-time control of autonomous VTOL UAVs for ship landing operations. J. Frankl. Inst. 2020, 357, 6175–6196. [Google Scholar] [CrossRef]
- Liu, C.; Fang, S.; Li, J.; Gao, B. An Adaptive Dual-Docking Force Control of Ship-Borne Manipulators for UAV-Assisted Perching. In Proceedings of the 2024 IEEE 14th International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Copenhagen, Denmark, 16–19 July 2024; pp. 394–398. [Google Scholar] [CrossRef]










| Notations | Values | Units |
|---|---|---|
| Degrees of freedom | 6 | |
| Grasp workspace | ||
| End-effector payload | ||
| UAV (DJI mini) weight | ||
| Camera depth range | 1.0 | |
| Camera stand height | 0.3 | |
| Radar ranging error | 0.02 | |
| Ship size |
| Method | IBVS | UAV Autoland | |
|---|---|---|---|
| Confidence interval | |||
| Confidence interval | |||
| Confidence interval | |||
| Docking time | 42 | 53 | |
| Repeated trials | 8 | 8 | |
| Docking success rate | 87.5 | 75 | % |
| Peak contact force |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Liu, C.; Zhang, L.; Zhang, C.; Lian, J.; Wang, H.; Gao, B. Shipborne Stabilization Grasping Low-Altitude Drones Method for UAV-Assisted Landing Dock Stations. Drones 2026, 10, 52. https://doi.org/10.3390/drones10010052
Liu C, Zhang L, Zhang C, Lian J, Wang H, Gao B. Shipborne Stabilization Grasping Low-Altitude Drones Method for UAV-Assisted Landing Dock Stations. Drones. 2026; 10(1):52. https://doi.org/10.3390/drones10010052
Chicago/Turabian StyleLiu, Chuande, Le Zhang, Chenghao Zhang, Jing Lian, Huan Wang, and Bingtuan Gao. 2026. "Shipborne Stabilization Grasping Low-Altitude Drones Method for UAV-Assisted Landing Dock Stations" Drones 10, no. 1: 52. https://doi.org/10.3390/drones10010052
APA StyleLiu, C., Zhang, L., Zhang, C., Lian, J., Wang, H., & Gao, B. (2026). Shipborne Stabilization Grasping Low-Altitude Drones Method for UAV-Assisted Landing Dock Stations. Drones, 10(1), 52. https://doi.org/10.3390/drones10010052







