A Morphing Land–Air Robot with Adaptive Capabilities for Confined Environments

Highlights

What are the main findings?

• A morphing wheeled land–air robot is developed by integrating a multi-link foldable arm mechanism and a variable-diameter wheel mechanism to achieve land–air mode switching, in-flight morphing, flexible dual landing strategies, and smooth transitions between wheeled and legged locomotion.
• The study systematically investigates the aerodynamic effects induced by the addition of wheels, evaluates the performance of the two morphing mechanisms, and validates the robot’s performance through comprehensive outdoor tests, including obstacle traversal and folded takeoff/landing.

What are the implications of the main findings?

• The proposed design greatly enhances mobility and flexibility across air and ground environments, reducing unnecessary takeoffs, lowering energy consumption, and improving overall reliability.
• The unique multi-modal architecture forms a unified aerial–ground operational framework, offering higher efficiency, stability, and robustness when navigating complex real-world environments.

Abstract

Traditional wheeled ground robots offer high energy efficiency and excellent mobility on flat terrain but are constrained by their fixed structures, making it difficult to overcome obstacles or adapt to complex environments. To address these limitations, this paper presents a morphing wheeled land–air robot (MW-LAR) that integrates ground locomotion and quadrotor flight. By incorporating foldable arms and variable-diameter wheels, the MW-LAR can not only switch between ground and flight modes, but also achieve transitions between wheeled and legged locomotion in the ground mode. The foldable arms support seamless aerial-to-ground transitions and in-flight morphing, while the variable-diameter wheels facilitate efficient obstacle traversal on the ground. Benefiting from the design of foldable arms, two complementary landing approaches, namely direct quadrotor landing and ground-mode landing, are implemented to explore different aerial-to-ground transition modes and to improve landing safety and switching efficiency. Experimental results demonstrate that the MW-LAR achieves stable and energy-efficient performance across multiple locomotion modes and complex environments, highlighting its potential for integrated land–air mobility applications.

1. Introduction

Traditional unmanned aerial vehicles (UAVs) exhibit excellent long-range maneuverability and provide a wide field of view [1], but they also face limitations, such as limited endurance, payload capacity, and ability to fly in confined spaces [2,3,4]. Correspondingly, unmanned ground vehicles (UGVs) can operate for extended periods and carry heavy materials but are restricted by terrain and have poor spatial mobility [5]. Multi-modal robots that combine the flexibility of UAVs with the robustness of UGVs can effectively address both shortcomings and provide a balanced solution [6]. They can choose the optimal mode of action based on the actual environment and respond flexibly across various terrains and obstacle-dense scenarios, significantly improving mission execution efficiency. These advantages make them promising in various applications such as disaster rescue, environmental monitoring, and agricultural mapping [6,7], to name a few.

A variety of multi-modal robots have been developed in recent years. For example, the BogieCopter proposed in [8] consists of two tiltable axles and four independent passive wheels, and achieves multi-modal locomotion using the same set of actuators. The HyTAQ robot in [9] adds a cage-like structure to a basic quadrotor, allowing the entire body to act as a passive wheel for ground locomotion. However, this design greatly increases the robot’s size and introduces greater rotational resistance during turning, while its ground mode still relies on the propeller motors for actuation. The robot proposed in [10] employs independent motors to drive the wheels, which simplifies control, while its large size makes it prone to tipping over when climbing or crossing obstacles, making it difficult to maintain stability. In addition to the above works, there are quite a few remarkable works, including but not limited to [11,12], Drivocopter [13], SytaB [14], LEONARDO [15], Skywalker [16], and MALV [17].

At present, several studies have achieved mode switching of a multi-modal robot through structural morphing, enabling different modes to operate independently [18,19,20,21]. For example, the works [22,23,24,25] have reported a series of outstanding sprawl-tuned autonomous robots (STARs) with arms folded downward to achieve modal transition and propeller motors driving the wheels in wheel mode. However, the propeller would generate lateral force when the arm folded, which would be detrimental to the robot’s forward motion and lead to unnecessary energy consumption. In [23], the propellers can generate negative pressure when climbing the wall, but for normal driving, this design could hinder the speed of the robot’s movement, and the energy consumption increases accordingly. In [24], the clutch is added to drive propellers and wheels in a time-sharing manner, reducing driving energy consumption by 52% and achieving higher speed. However, the wheels still rotate along with the propeller during flight, which undoubtedly consumes unnecessary energy. The system complexity also increases. In summary, the advantage of using arm folding for mode transitions lies in preserving an efficient aerodynamic profile during flight while enabling a compact and stable mobile platform in ground mode, thereby enhancing the robot’s adaptability to complex environments. However, these multi-modal robots still face limitations: the arm folding angles are typically constrained, so these robots often need to land in a quadrotor configuration before transforming into ground mode, which may pose considerable challenges on unstructured terrain. Since the arms cannot be folded in the air, these robots often have to bypass narrow spaces or pass through them with a significant tilt. In ground mode, encountering obstacles typically requires frequent takeoffs and landings, resulting in increased energy consumption. Due to the compact nature of the structure, adding wheels near propellers will inevitably affect the lift, which is something few works have investigated.

To address the limitations of conventional multi-modal platforms, we propose a morphing wheeled land–air robot (MW-LAR) with enhanced environmental adaptability, designed with a focus on structural simplicity and control efficiency, as shown in Figure 1. The robot features optimally designed foldable arms that enable seamless transitions between flight and ground modes, as well as in-flight morphing to improve maneuverability in confined or cluttered environments. Moreover, the MW-LAR supports two landing strategies: one performed directly in the flight mode, and the other achieved by folding the arms into a configuration close to the ground mode, thereby ensuring higher reliability under various terrain conditions. In ground mode, the robot uses variable-diameter wheels to cross non-flying obstacles, eliminating the need for repeated takeoffs and thereby reducing energy consumption. In addition, the wheels are independently driven and fully decoupled from the propulsion motors, allowing the robot to move quietly during close-range inspection or reconnaissance tasks, which enhances both operational safety and stealth capability. This work has four layers of contributions. (i) Two morphing mechanisms: the MW-LAR achieves mode transformation through two mechanisms: a multi-link structure enabling transitions between flight and ground modes, and a modular scissor-type design allowing the wheels to switch between wheeled and legged locomotion. (ii) Aerodynamic effects investigation: the aerodynamic effects of the propeller partially overlapping the body and wheels are extensively studied and tested through simulations and experiments, which are rarely studied in existing related work. (iii) Aerial–ground transition mechanism: two complementary landing approaches (flight-mode landing and ground-mode landing) are developed to explore different aerial-to-ground transitions, improving the safety and adaptability of mode switching. (iv) In-flight morphing: there is little research on multi-modal robots that can dynamically adjust the body by folding the robotic arms during flight to improve environmental adaptability. Finally, a systematic platform is constructed and experimentally validated to demonstrate the MW-LAR’s ability to combine multiple modes to accomplish various maneuvers.

This paper is organized as follows. Section 2 describes the overall design of the MW-LAR, mainly focusing on the morphing and actuation mechanisms of the robot in different modes, as well as its obstacle-crossing strategy in the ground mode. Section 3 establishes the dynamic model of the MW-LAR in the flight mode, analyzes the forces during the landing process, and further investigates its force distribution and stability characteristics when crossing obstacles in the ground mode. Section 4 develops the flight-mode control framework of the MW-LAR, presents the design of attitude and position controllers, and validates their effectiveness through simulation experiments. Section 5 presents a series of experiments to validate the performance of the robot. Finally, we conclude our work.

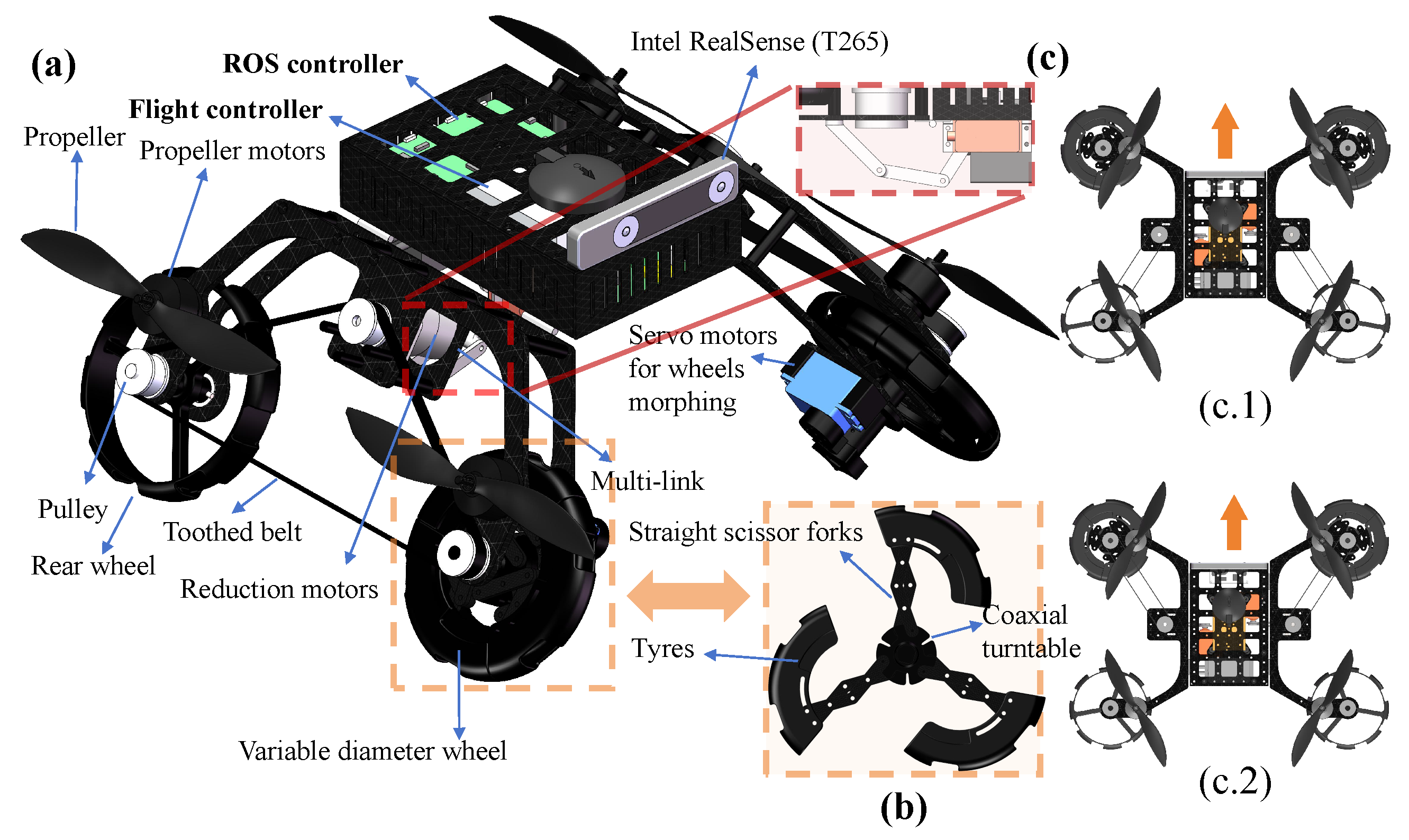
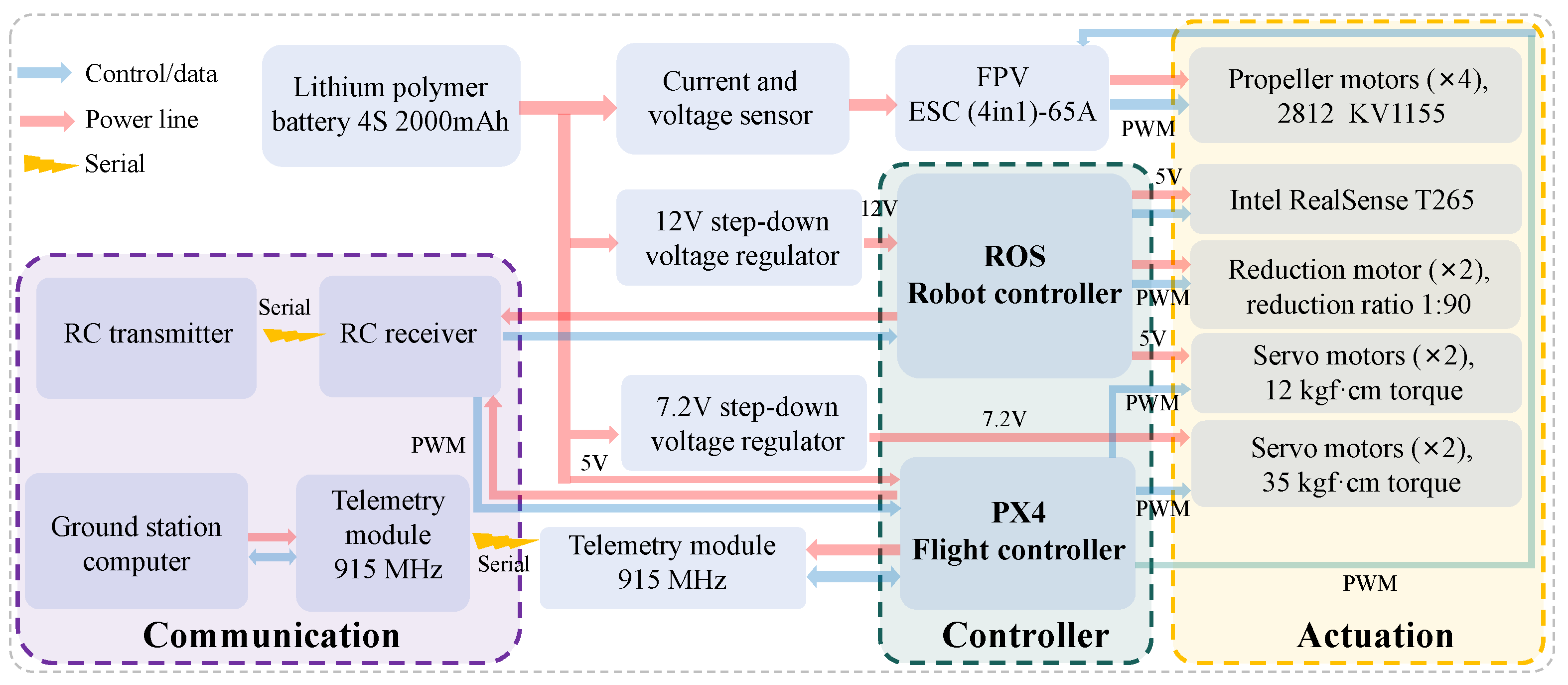
2. Robot’s System Design

This section first provides an overview of the robot’s overall structure and working principle, then describes the design of its morphing mechanisms and driving methods in both flight and ground modes, and finally presents the obstacle-crossing strategy in the ground mode.

2.1. System Overview of the MW-LAR

Figure 2a demonstrates the overall design and detailed components of the MW-LAR. When the MW-LAR is in a horizontal state, that is, in flight mode, it is no different from a traditional quadrotor, with four motors that provide lift evenly distributed around the body. The difference is that the MW-LAR is equipped with two foldable arms, which enable the robot to perform mid-air morphing and transform into ground mode. In ground mode, the MW-LAR can be regarded as a mobile robot with four wheels: two ordinary wheels at the rear and two variable-diameter wheels at the front, whose diameters are actively adjusted according to the terrain. For land–air robots, we also need to pay attention to the layout of propellers and wheels during installation. Theoretically, there are two ways to install the wheels: one is above the propeller and the other is below. Given that placing the wheel above the propeller would increase pressure on the body frame and cause instability, this study adopts the method of placing the wheel below the propeller. The next question is to determine the vertical mounting distance between the wheel and the propeller. We determined this through a series of pre-tests, and the results showed that when this distance varies between 2 cm and 8.5 cm, the impact on the propeller’s lift induced by the wheel is not much different. Therefore, for the sake of compactness, we preset this vertical distance to 2 cm. The main performance parameters are summarized in

Table 1. Main specifications of the MW-LAR.

MW-LAR	Parameters
Robot size ($\alpha$ = $0^{\circ }$)	394 × 504 × 125 mm
Robot size ($\alpha$ = ${90}^{\circ }$)	394 × 300 × 259 mm
Deployment angle of the arm	$0^{\circ }\le$$\alpha$$\le {83}^{\circ }$
Deployment angle of scissors	${32}^{\circ }\le$$\beta$$\le {139}^{\circ }$
Wheel’s size	65$\le r_w\le$110 mm
Minimum traversal width	255 mm
Minimum traversal height	167 mm
Maximum folding angle during in-flight morphing	${83}^{\circ }$
Turning radius	360° turn in place
In-flight morphing	Maintain stable In-flight Morphing
Average current during hovering ($\alpha$ = $0^{\circ }$)	11 A
Average current (ground mode)	0.2 A
Average current (folding on concrete floor)	0.3 A
Instantaneous current during diameter change	0.9 A

.

2.2. Motion Mechanisms

The morphing design of the MW-LAR is primarily reflected in its foldable arms and variable-diameter wheels. The foldable arms enable in-flight morphing and modal transitions, while the variable-diameter wheels change size to cross obstacles. Building on our previous work [26], the following section revolves around the mechanism design of the foldable arm and the variable-diameter wheel.

In [26], we used a gear set to achieve arm folding, but it has disadvantages such as low efficiency, poor accuracy, a complex structure, easy wear, and a high required torque. The foldable arm of the MW-LAR uses a multi-link mechanism and can theoretically achieve a folding angle of $0\sim {90}^{\circ }$ with high efficiency, high accuracy, a simple structure, and low required torque. When the robot lands in a quadrotor shape, the corresponding arm is in a completely horizontal state. Then, by controlling the angle between the foldable arm and the horizontal line during the arm’s downward rotation, the transition of the flight mode to ground mode can be achieved. Conversely, the arms rotate upwards to return to flight mode. Moreover, the arms can be folded before landing, allowing the robot to approach a configuration closer to ground mode and then complete further folding upon touchdown. Similarly, the quadrotor can also achieve mid-air morphing in this way.

To adapt to complex terrain, the variable-diameter wheels of the MW-LAR employ a hinged structure based on rigid straight scissor elements (SSEs), in which relative rotation between two coaxial discs changes the angles between adjacent scissor links, thereby enabling adjustment of wheel diameter. Based on this design, the variable-diameter wheel exhibits two modes: wheeled mode and legged mode, as shown in Figure 2b. In wheeled mode, the wheel remains folded, with the scissor mechanism contracting to a smaller diameter suitable for narrow spaces. In legged mode, the wheel is in the unfolded state, with the scissor mechanism fully extended to enlarge the wheel’s diameter, enabling effective obstacle crossing. When encountering different terrains or obstacles, the robots can adjust the size of their wheels to match the specific terrain or obstacle. In addition, the wheels feature a modular design and are belt-driven, allowing them to be configured as front-wheel drive, rear-wheel drive, or all-wheel drive, as shown in Figure 2c. This modular structure facilitates easy disassembly and replacement in the event of damage.

2.3. Actuation Mechanisms

Figure 3 illustrates the controller and actuation designed for the MW-LAR. Overall, the robot is powered by a 4S Lipo battery, which is then stepped down to a suitable voltage to power the controllers and actuators. The power drive for the MW-LAR in flight mode consists of 4 propeller motors (2812 KV 1155,T-Motor, Nanchang, China) with 8040 3-blade propellers(Gemfan, Ningbo, China), controlled by the flight controller PX4(Pixhawk 6C Mini, Holybro, Shenzhen, China) through a 4-in-1 ESC(Hobbywing, Shenzhen, China). Two reduction motors with a 1:90 reduction ratio are distributed on the left and right sides of the robot body and drive the synchronous wheels via belts. The whole process is controlled by the ROS controller. The reduction motor installation position uses a modular slide design, which facilitates quick replacement and allows easy adjustment of the installation position to match the system’s center of gravity. The MW-LAR’s morphing mainly involves folding the arms and changing the wheels’ diameters. The former adopts two high-voltage servo motors (35 kgf·cm) to synchronously drive the two arms on both sides of the body to fold up and down to adjust the body size. The latter employs two low-voltage servo motors (12 kgf·cm) to synchronously drive the variable-diameter wheels. Both types of servo motors for morphing are controlled by the PX4 controller.

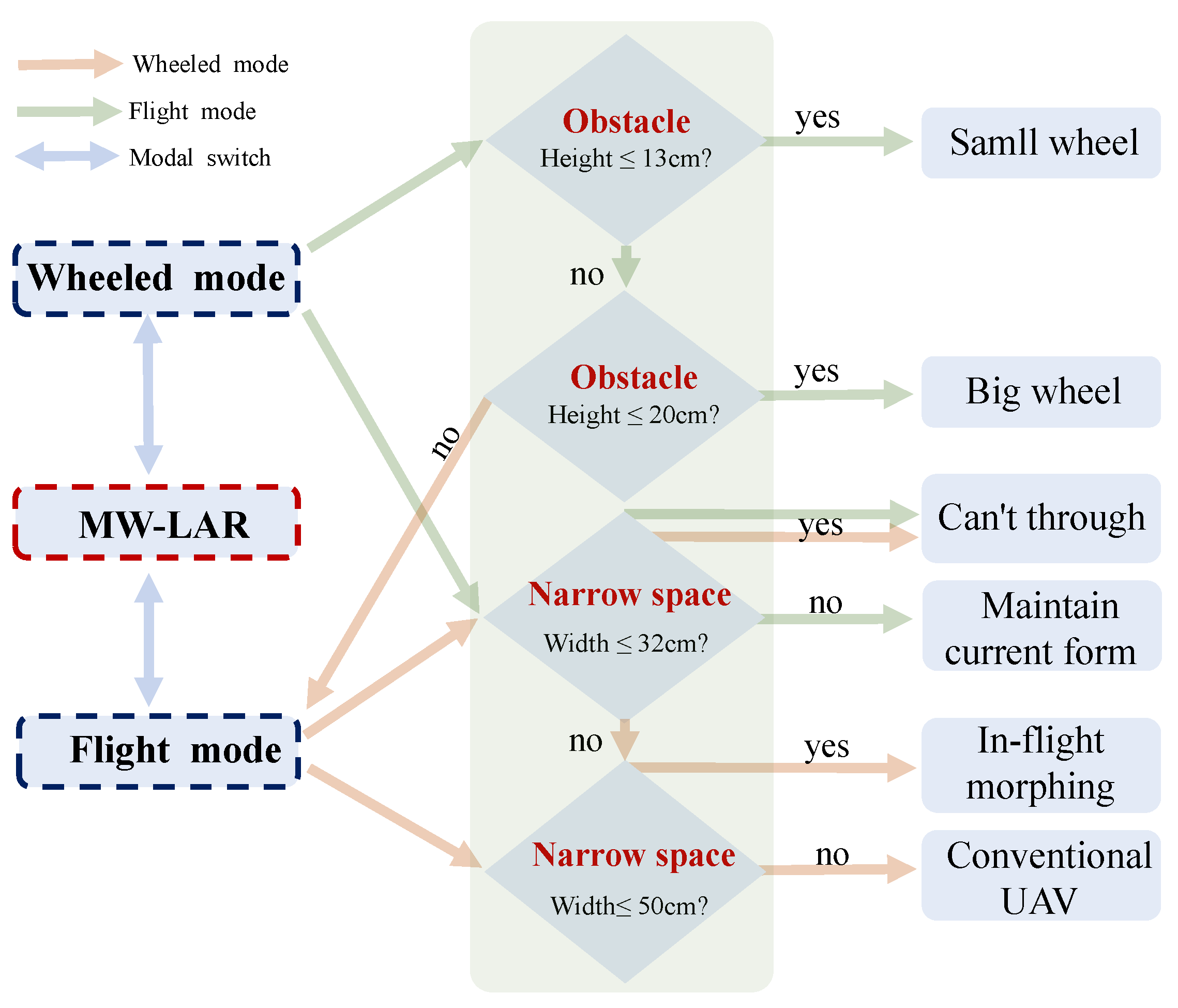
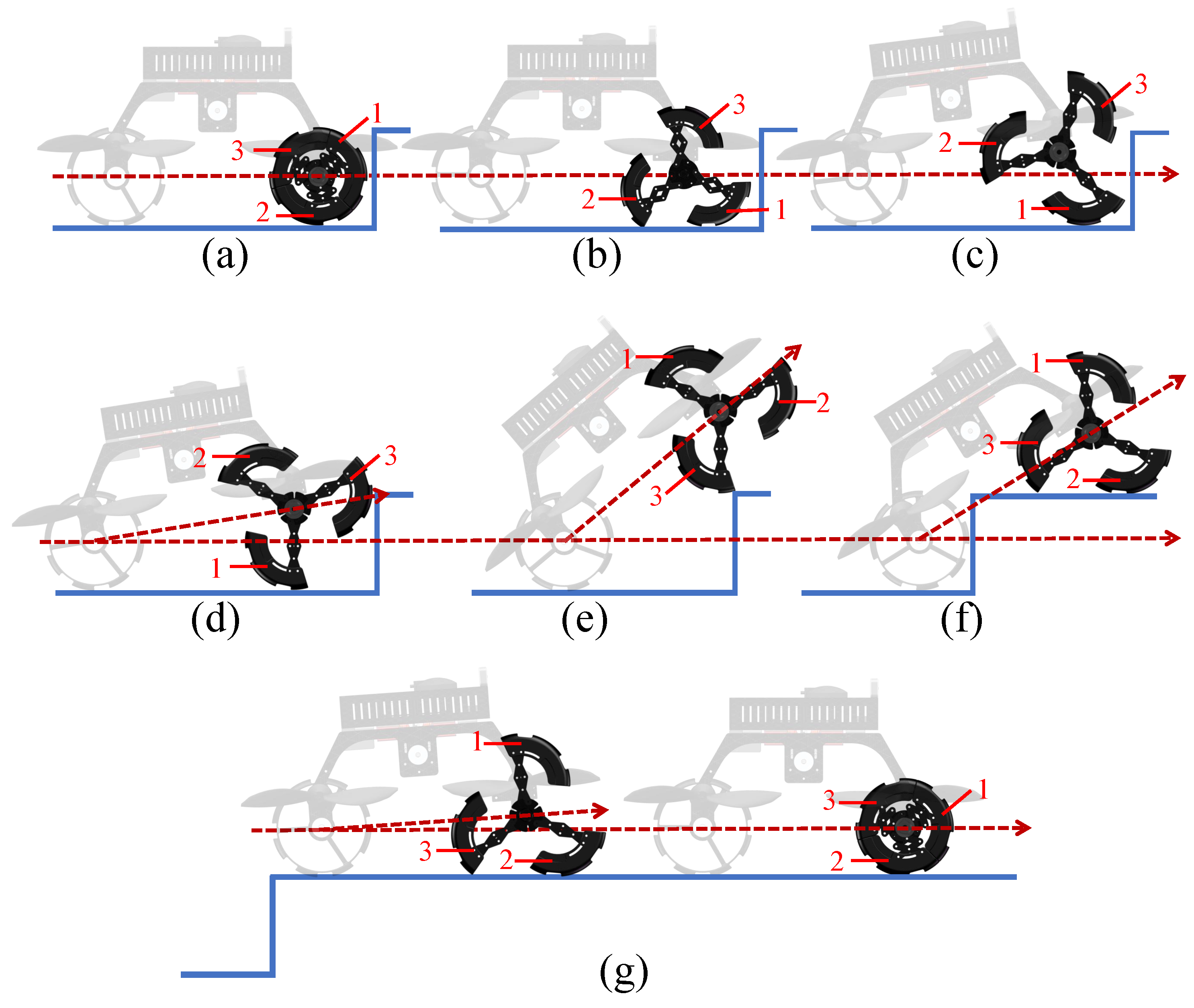
2.4. Overcoming Obstacles Strategy

Assuming that the dimensions of the obstacles are known and the height of the narrow space is sufficient, the detailed obstacle-avoidance strategy is illustrated in Figure 4. For obstacle heights $H\le 13$ cm, the MW-LAR can overcome them directly in a non-variable-diameter state. For $H\in (13,20]$ cm, the traditional ground-aerial robots typically need to take off again to cross, whereas the MW-LAR can extend its wheels to a larger diameter, successfully overcoming the obstacle. When $H>20$ cm, the MW-LAR switches to flight mode to surmount the obstacle. When navigating narrow passages, the MW-LAR can smoothly pass through widths of $W\in [32,50]$ cm by folding its arms, both in ground and flight modes. For $W>50$ cm, the robot maintains its original shape without morphing. If $W<32$ cm, i.e., smaller than its minimum body width, the robot cannot pass.

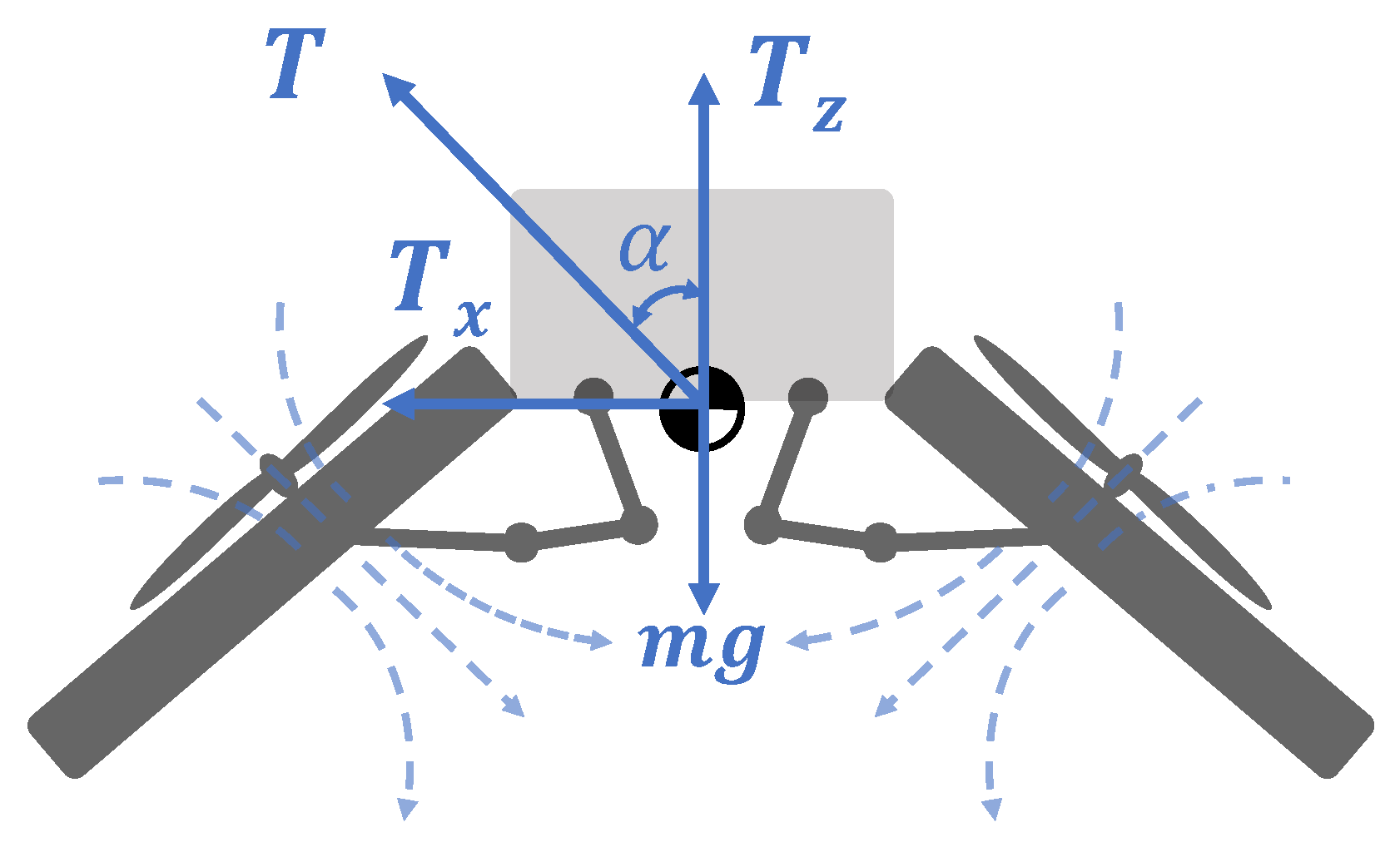
3. Dynamic Modeling of the Robot

This section analyzes the force characteristics of the MW-LAR in different working modes. First, the forces in the flight mode are analyzed to provide a basis for subsequent controller design. Next, the forces during the landing process are examined to determine an appropriate landing posture. Finally, the force distribution and stability conditions during step-climbing in the ground mode are analyzed.

3.1. Dynamics in Flight Mode

A traditional quadrotor can be modeled as a rigid-body system, whose dynamics follow the Newton–Euler equations. Specifically, the translational dynamics are given by

$$\ddot{\mathit{p}}={\displaystyle \frac{1}{m}}R\mathit{T}-\mathit{g}{\mathit{e}}_3.$$

(1)

In addition, the rotational dynamics can be expressed as

$$I\dot{\mathit{\omega }}+\mathit{\omega }\times \left(I\mathit{\omega }\right)=\mathit{\tau },$$

(2)

where $\mathit{p}={[x,y,z]}^{\mathrm{T}}$ denotes the position of the robot’s center of mass in the world frame, and $\ddot{\mathit{p}}$ is the acceleration of the center of mass. m is the mass of the robot, and R represents the rotation matrix from the body frame to the world frame. $\mathit{T}$ denotes the total thrust expressed in the body frame, $\mathit{g}$ is the gravitational acceleration, and ${\mathit{e}}_3={[0,0,1]}^{\mathrm{T}}$ is the unit vector along the z-axis of the world frame. I is the inertia matrix, and $\mathit{\omega }={[{\omega }_x,{\omega }_y,{\omega }_z]}^{\mathrm{T}}$ is the angular velocity vector representing roll, pitch, and yaw rates. Finally, $\mathit{\tau }={[{\tau }_x,{\tau }_y,{\tau }_z]}^{\mathrm{T}}$, where ${\tau }_x$, ${\tau }_y$, and ${\tau }_z$ represent the roll, pitch, and yaw torques in the body frame, respectively. For conventional quadrotor configurations, the total thrust generated by the rotors is aligned with the body-frame z-axis, and the inertia matrix I is typically regarded as constant. In contrast, for a morphing quadrotor, the introduction of the folding angle $\alpha$ causes both a deviation of the total thrust direction from the body-frame z-axis and a redistribution of the system mass. Consequently, the total thrust expressed in the body frame can be written as $\mathit{T}={[Tsin\alpha ,0,Tcos\alpha ]}^T$, and the inertia matrix becomes a function of the folding angle, i.e., $I=I\left(\alpha \right)$. The robot can be decomposed into several geometric components. In detail, the main body is modeled as a cuboid with mass $m_1$ and dimensions a, b, and c. The reduction motor is modeled as a cylinder with mass $m_2$, radius $r_1$, and height $h_1$. The propeller, together with the motor, is modeled as a cylinder with mass $m_3$, radius $r_2$, and height $h_2$. The inertia matrix of each component in its own center-of-mass frame can be expressed as follows $I_i=\mathrm{diag}({\displaystyle \frac{m_i{l}_{i_1}}{12}},{\displaystyle \frac{m_i{l}_{i_2}}{12}},{\displaystyle \frac{m_i{l}_{i_3}}{12}})$, where $i=1,2,3$, and $I_1$, $I_2$, and $I_3$ denote the inertia matrices of the main body, the reduction motor, and the propeller together with the motor, respectively. Then, the parameters $l_{i_j}$ are defined as $l_{1_1}=a^2+b^2$, $l_{1_2}=a^2+c^2$, $l_{1_3}=b^2+c^2$, $l_{2_1}=3(r_1^2+h_1^2)$, $l_{2_2}=3(r_1^2+h_1^2)$,$l_{2_3}=6r_1^2$, $l_{3_1}=3(r_2^2+h_2^2)$, $l_{3_2}=3(r_2^2+h_2^2)$, and $l_{3_3}=6r_2^2$. In addition, the inertia matrices of the reduction motor and the propeller, together with the motor, need to be translated to the body-frame center of mass using the parallel axis theorem. If the arm rotates about the x-axis by an angle $\alpha$, a rotation matrix can be used to describe this rotation,

$$R_x\left(\alpha \right)=\left[\begin{array}{ccc}1& 0& 0\\ 0& cos\alpha & -sin\alpha \\ 0& sin\alpha & cos\alpha \end{array}\right].$$

The inertia matrices of the motor and propeller are adjusted to obtain the inertia matrix expressed in the body frame.

$$I_i\left(\alpha \right)=R_x\left(\alpha \right)I_i{R}_x^T\left(\alpha \right),i\in \{2,3\}.$$

Therefore, the overall inertia matrix of the robot is given by

$$I\left(\alpha \right)=I_1+2R_x\left(\alpha \right)I_2{R}_x^T\left(\alpha \right)+4R_x\left(\alpha \right)I_3{R}_x^T\left(\alpha \right).$$

(3)

Substituting Equation (3) into Equation (2) results in the attitude dynamics model of the morphing quadrotor.

$$I\left(\alpha \right)\dot{\omega }+\dot{I}\left(\alpha \right)\omega +\omega \times \left(I\left(\alpha \right)\omega \right)=\mathit{\tau }.$$

(4)

In addition, the folding angle $\alpha$ changes the orientation of the rotor moment arms, thereby altering the mapping between thrust and torque. The rotor speed vector is defined as ${\mathbf{\Omega }}^2={\left[\begin{array}{c}{\omega }_1^2,{\omega }_2^2,{\omega }_3^2,{\omega }_4^2\end{array}\right]}^T$, where ${\omega }_i$ ($i=1,2,3,4$) denotes the angular velocity of the i-th rotor. Therefore, the thrust-torque relationship of the morphing quadrotor can be expressed as ${[T,{\tau }_x,{\tau }_y,{\tau }_z]}^T=\mathit{M}\left(\alpha \right){\mathbf{\Omega }}^2$, where the control allocation matrix is defined as $\mathit{M}\left(\alpha \right)={\left[\begin{array}{c}{a}_1,a_2,a_3,a_4\end{array}\right]}^T$ with $a_1=-bcos\alpha {\mathbf{J}}^T$, $a_2={\displaystyle \frac{\sqrt{2}}{2}}(lb+ksin\alpha ){\mathbf{s}}_x^T$, $a_3={\displaystyle \frac{\sqrt{2}}{2}}(lb-ksin\alpha ){\mathbf{s}}_y^T$, $a_4=kcos\alpha {\mathbf{s}}_z^T$, where $\mathbf{J}={[1,1,1,1]}^T$, ${\mathbf{s}}_x={[-1,1,1,-1]}^T$, ${\mathbf{s}}_y={[1,1,-1,-1]}^T$, and ${\mathbf{s}}_z={[1,-1,1,-1]}^T$. The parameters b, k, and l denote the thrust coefficient, torque coefficient, and the distance from each rotor to the center of mass, respectively. It should be noted that this model neglects aerodynamic effects and is primarily applicable to deformation and configuration transition processes under low-speed flight conditions.

3.2. Landing Force Analysis in Flight Mode

Traditional ground-aerial robots usually land in flight mode and transition to ground mode upon touchdown. In complex or unstructured terrains, this process can be risky, as unstable landings or failed transformations may affect subsequent tasks. In contrast, if a robot can land in a posture closer to its ground mode, it can switch more quickly and reliably upon contact, enhancing both the stability and continuity of task execution.

Accordingly, we analyzed the landing forces acting on the robot when its arms are folded, as illustrated in Figure 5. In this analysis, ground effect is neglected, as the focus is on the robot at altitudes where ground effect is minimal and on the balance between thrust and gravity for different arm folding angles. At these heights, the additional lift generated by airflow reflection is negligible. In practice, ground effect produces an upward aerodynamic force that can reduce impact and improve stability during landing. Therefore, if the analysis without ground effect meets the landing safety requirements, the actual scenario provides an even greater safety margin. The corresponding force relationships during landing can be expressed as $T_z=Tcos\alpha$, where T denotes the total thrust, $\alpha$ is the folding angle of the arms, and $T_z$ and $T_x$ represent the vertical and horizontal components of T, respectively. When $\alpha =0^{\circ }$, the thrust is fully aligned with the vertical direction, allowing it to completely counteract gravity while maintaining sufficient control authority. As $\alpha$ increases, the vertical component of thrust decreases accordingly, leading to a reduction in attitude regulation and disturbance rejection capability. Based on this analysis, a critical folding angle, ${\alpha }_c$, can be defined as the maximum folding angle at which the robot just balances its weight under maximum thrust, $F_{max}$. From the force equilibrium relation $F_{max}cos{\alpha }_c=mg$ and the thrust-to-weight ratio $F_{max}/mg=2.2$, the critical angle is calculated as ${\alpha }_c\approx {63}^{\circ }$. This result indicates that when $\alpha <{63}^{\circ }$, the robot is able to maintain hovering with sufficient control margin. In contrast, when $\alpha \ge {63}^{\circ }$, the entire thrust is consumed to counteract gravity, leaving the system with almost no disturbance rejection capability, thus even minor perturbations may lead to instability and significantly increase the risk during landing.

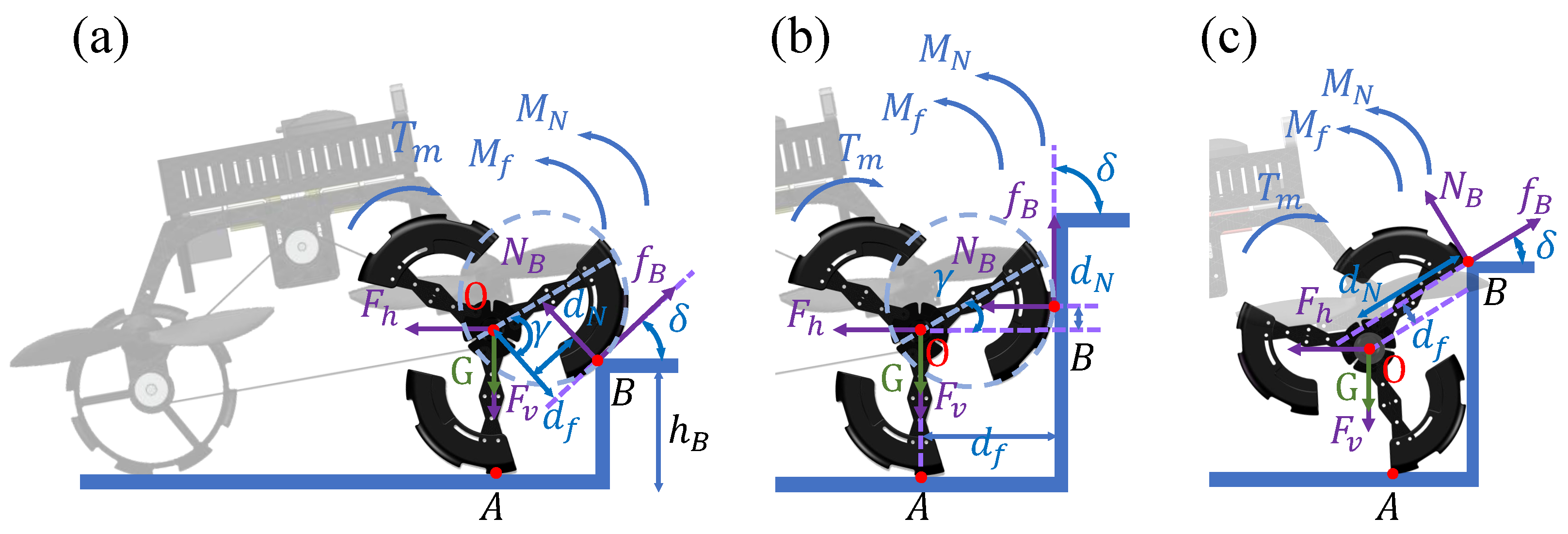
3.3. Obstacle-Crossing Force Analysis in Ground Mode

To clearly illustrate the role of the variable-diameter mechanism and the wheel-leg mode transition during obstacle traversal, the detailed process of the robot overcoming an obstacle is presented below (see Figure 6a–g). During obstacle traversal, when the wheels contact the obstacle, the robot adjusts the wheel diameter to match the obstacle height, allowing the wheel-leg structure to smoothly transition from wheel mode to leg mode. Branch leg 3 then contacts the edge of the step, generating upward diagonal friction to support the robot, while branch leg 2 rotates downward until it touches the obstacle, enabling the front wheel to successfully climb over it. After the front wheel clears the obstacle, the rear wheel completes the traversal, driven by the combined effect of the center-of-mass shift and traction from the front wheel. Finally, the wheel-leg structure switches back from leg mode to wheel mode, allowing the robot to continue forward.

In the study of wheel-leg climbing on steps, the climbing modes of the wheel-leg can be divided into three types based on the relative relationship between the step height and the wheel-leg diameter, as well as the motion characteristics of the wheel-leg, as shown in Figure 7. The first is pedaling climbing, in which the wheel-leg generates an upward thrust by pedaling on the step, and achieves upward movement by utilizing the ground reaction force and friction. This climbing mode is not limited by the step height and can be used for step heights below or above the leg diameter. The second case is a special case of the first one. When the step height is greater than the wheel-leg diameter, the tangent at the contact point between the wheel-leg and the step is upward, and the wheel-leg primarily relies on friction to overcome gravity for climbing. The third is grasping climbing, which applies when the step height is lower than the wheel-leg diameter. The wheel-leg contacts the upper surface of the step at its front end and generates an upward pulling force through grasping actions to achieve climbing.

To investigate the force conditions required for the robot during obstacle crossing, the force situation of a single wheel-leg unit during climbing needs to be analyzed. When endpoint A of the wheel-leg is about to detach from the lower surface of the step, it marks the critical point for the robot to begin climbing, and the force analysis is shown in Figure 7. In the figure, $F_h$ and $F_v$ are the horizontal and vertical components of the force from the robot’s body on the wheel-leg, respectively, $N_B$ and $f_B$ are the normal force and frictional force at the contact point between the wheel-leg and step corner, respectively, G is the gravity of the wheel-leg itself, $M_N$ and $M_f$ are the moments of force $N_B$ and $f_B$ about the geometric center O of wheel-leg, respectively, $T_m$ is the driving torque provided by the motor, $\delta$ is the angle between the tangent at the contact point of the wheel-leg and the step, and the horizontal surface of the step, $\gamma$ is the angle between the normal to the friction force line and the wheel leg arm, and $d_N$ and $d_f$ are the vertical and horizontal components of the distance between points B and O, respectively. The directions of the forces indicated are their positive directions, not the actual directions during climbing. It should be noted that, since the present analysis focuses solely on the local critical state of the variable-radius wheel at the instant of obstacle crossing, rather than the complete force equilibrium of the entire robot, the ground reaction forces at the rear wheels are neglected in this analysis.

First, as illustrated in Figure 7a, from the balance of forces, it can be expressed as follows

$$\begin{array}{cc}\hfill F_h-f_{B}cos\delta +N_{B}sin\delta & =0,\hfill \\ \hfill F_v+G-f_{B}sin\delta -N_{B}cos\delta & =0,\hfill \\ \hfill T_m-M_f-M_N& =0,\hfill \\ \hfill M_f& =f_B{d}_f,\hfill \\ \hfill M_N& =N_B{d}_N,\hfill \end{array}$$

(5)

where $d_f=r_0+\Delta r_{\omega }cos\gamma$, $d_N=\Delta r_{\omega }tan\gamma cos\gamma$, $\Delta r_{\omega }=r_{\omega }-r_0$, and $r_0$ denotes the original radius of the wheel-leg.

If a wheel-leg of the variable-diameter wheel reaches the critical slipping condition at contact point B, $N_B$ and $f_B$ satisfy $f_B=\mu N_B$, where $\mu$ is the coefficient of static friction between the wheel and the obstacle surface. Substituting this equation into the first equation of Equation (5) yields $F_h=N_B(\mu cos\delta -sin\delta )$. Under the critical condition $F_h=0$, the critical angle is given by ${\delta }_c=arctan\mu$. Therefore, when $\delta <{\delta }_c$, $F_h>0$, indicating that the friction force can provide forward driving force. Conversely, when $\delta >{\delta }_c$, $F_h<0$, and the system exhibits a tendency to slip. It should be noted that $\delta ={90}^{\circ }$ represents a special case, as shown in Figure 7b. Similarly, for the force configuration illustrated in Figure 7c, the force relations are the same as in Equation (5).

From the above analysis, when the wheel-leg endpoint A is about to leave the lower surface of the step, the corresponding $F_h$ and $F_v$ represent the minimum driving forces required for the robot to successfully climb. Conversely, when the contact point B is at the critical slipping condition, the corresponding $F_h$ and $F_v$ indicate the maximum driving forces the wheel-leg can sustain. According to Equation (5), these forces can be calculated as $F_h=N_B(\mu cos{\delta }_c-sin{\delta }_c)$ and $F_v=N_B(\mu sin{\delta }_c-cos{\delta }_c)$.

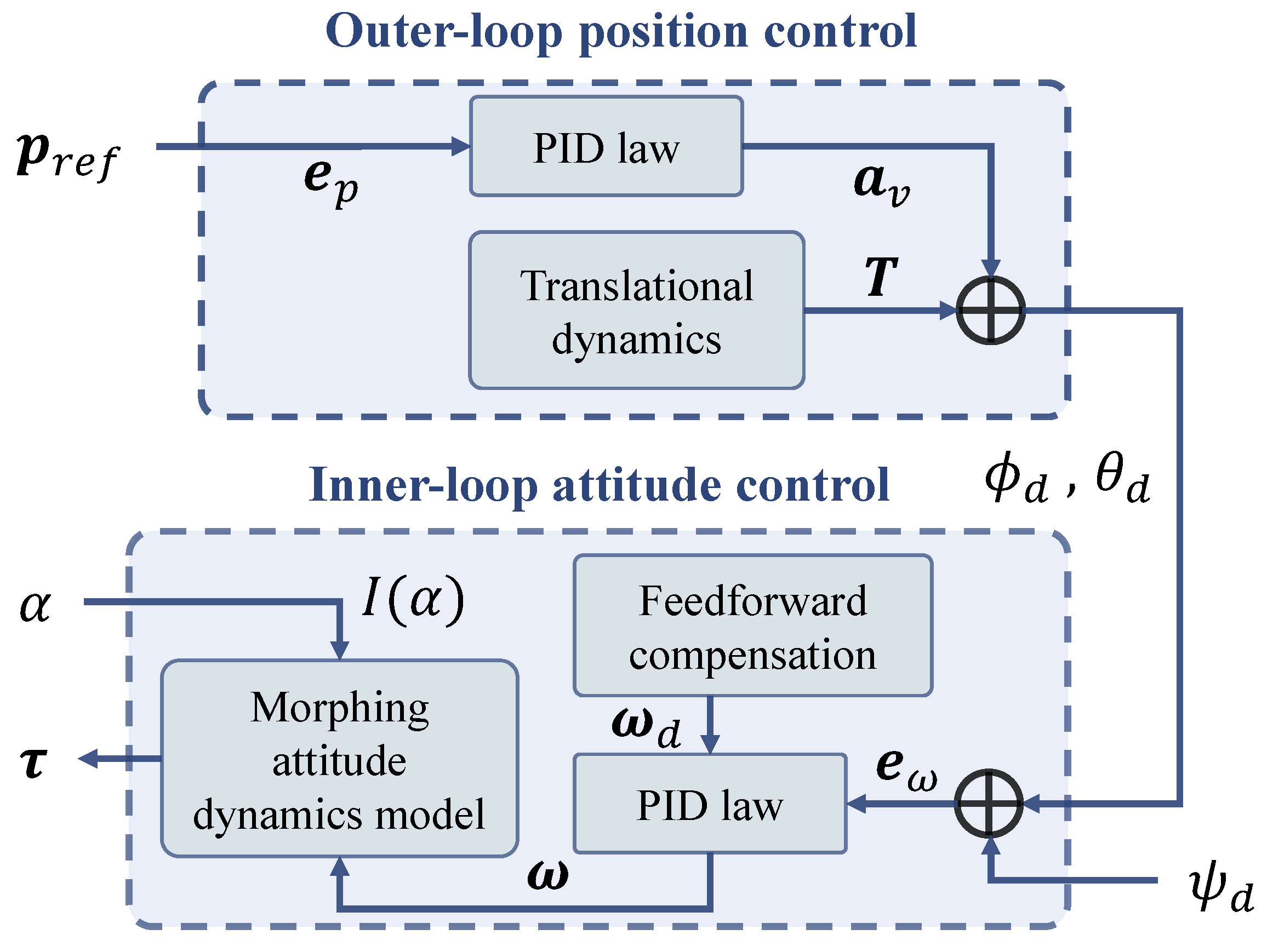
4. Control Design in Flight Mode

In this study, a hierarchical control architecture is adopted for the robot, with the inner loop responsible for attitude stabilization and the outer loop for position tracking. The control strategy is shown in Figure 8, providing stable control conditions for the flight experiments and enabling a better evaluation of the robot’s performance in flight mode.

4.1. Outer Loop Control

The outer-loop controller aims to track position with the basic idea of generating a virtual acceleration command ${\mathit{a}}_v={[a_{vx},a_{vy},a_{vz}]}^T$ based on the position error, which is then converted into the desired attitude angles through the translational dynamics equations. According to the reference trajectory ${\mathit{p}}_{ref}\left(t\right)$, the position error is defined as ${\mathit{e}}_p\left(t\right)={\mathit{p}}_{ref}\left(t\right)-\mathit{p}\left(t\right)$. The virtual acceleration command is then generated by a PID control law.

$${\mathit{a}}_v\left(t\right)=K_p{\mathit{e}}_p\left(t\right)+K_d{\mathit{e}}_p\left(t\right)+K_i{\int }_0^t{\mathit{e}}_p\left(\tau \right)d\tau ,$$

where $K_p$, $K_d$, and $K_i$ denote the proportional, derivative, and integral gains, respectively.

To satisfy Equation (1), the translational thrust is chosen as $T\left(t\right)=m|{\mathit{a}}_v\left(t\right)+g{\mathit{e}}_3|$, from which the desired attitude angles can be derived accordingly.

$$\begin{array}{cc}\hfill {\varphi }_d\left(t\right)& =arcsin\left({\displaystyle \frac{a_{vx}sin{\psi }_d-a_{vy}cos{\psi }_d}{\parallel {\mathit{a}}_v+g{\mathit{e}}_3\parallel }}\right),\hfill \\ \hfill {\theta }_d\left(t\right)& =arctan\left({\displaystyle \frac{a_{vx}cos{\psi }_d+a_{vy}sin{\psi }_d}{a_{vz}+g}}\right),\hfill \end{array}$$

where ${\psi }_d$ denotes the desired yaw angle, ${\mathit{e}}_3={[0,0,1]}^T$ represents the unit vector along the positive direction of the z-axis. Consequently, the outer loop converts the desired position trajectory into attitude angle commands, which serve as reference inputs for the inner-loop controller.

4.2. Inner Loop Control

In the inner-loop control, the traditional quadrotor angular-rate PID scheme is modified by incorporating the inertia matrix $I\left(\alpha \right)$, which varies with the folding angle, and by compensating for angular momentum coupling, thereby maintaining attitude tracking accuracy and stability during arm folding.

Given the reference attitude angles ${\mathsf{\Theta }}_d={[{\varphi }_d,{\theta }_d,{\psi }_d]}^T$, where ${\varphi }_d$ and ${\theta }_d$ are provided by the outer-loop controller and ${\psi }_d$ is determined by the mission planner, the angular velocity error is defined as ${\mathit{e}}_{\omega }={\mathit{\omega }}_d-\mathit{\omega }$, where ${\mathit{\omega }}_d={\dot{\mathsf{\Theta }}}_d$ denotes the reference angular velocity and $\mathit{\omega }=\dot{\mathsf{\Theta }}$ denotes the actual angular velocity. Based on this error, the desired angular accelerations in the three axes are computed by combining their integral and derivative terms with a feedforward compensation, as follows

$$\mathit{u}=K_p^{\omega }{\mathit{e}}_{\omega }+K_i^{\omega }\int {\mathit{e}}_{\omega }dt+K_d^{\omega }{\dot{\mathit{e}}}_{\omega }+K_{ff}^{\omega }{\mathit{\omega }}_d,$$

(6)

where $\mathit{u}={[{\dot{\omega }}_x,{\dot{\omega }}_y,{\dot{\omega }}_z]}^T$ represents the desired angular accelerations along the roll, pitch, and yaw axes.

By substituting Equation (6) into Equation (4), the angular rate control law is given as follows.

$$\begin{array}{cc}\hfill \mathit{\tau }=& I\left(\alpha \right)(K_p^{\omega }{\mathit{e}}_{\omega }+K_i^{\omega }\int {\mathit{e}}_{\omega }dt+K_d^{\omega }{\dot{\mathit{e}}}_{\omega })+\mathit{\omega }\times \left(I\left(\alpha \right)\mathit{\omega }\right)+K_{ff}^{\omega }{\mathit{\omega }}_d,\hfill \end{array}$$

(7)

where $K_p^{\omega }$, $K_i^{\omega }$, and $K_d^{\omega }$ are the feedback gains, while $K_{ff}^{\omega }$ is an optional feedforward gain.

By discretizing Equation (7) over the control period $\Delta t$, the following iterative form can be obtained.

$$\begin{array}{cc}\hfill \mathit{\tau }\left(k\right)=& I\left(\alpha \left(k\right)\right)(K_p^{\omega }{\mathit{e}}_{\omega }\left(k\right)+K_i^{\omega }{I}_e\left(k\right)+K_d^{\omega }{D}_e\left(k\right))\hfill \\ \hfill & +\mathit{\omega }\left(k\right)\times \left(I\left(\alpha \left(k\right)\right)\mathit{\omega }\left(k\right)\right)+K_{ff}^{\omega }{\mathit{\omega }}_d\left(k\right),\hfill \end{array}$$

(8)

where $I_e\left(k\right)=I_e(k-1)+{\mathit{e}}_{\omega }\left(k\right)\Delta t$ and $D_e\left(k\right)=({\mathbf{e}}_{\omega }\left(k\right)-{\mathbf{e}}_{\omega }(k-1))/\Delta t$, while $I\left(\alpha \right(k\left)\right)$ denotes the inertia matrix corresponding to the current folding angle. Within each control period $\Delta t$, the inner-loop controller computes the output torque $\mathit{\tau }\left(k\right)$ based on the latest measured states, compensating for variations in the folding-arm structure to maintain attitude tracking accuracy and system stability, thereby providing a reliable control foundation for the flight experiments.

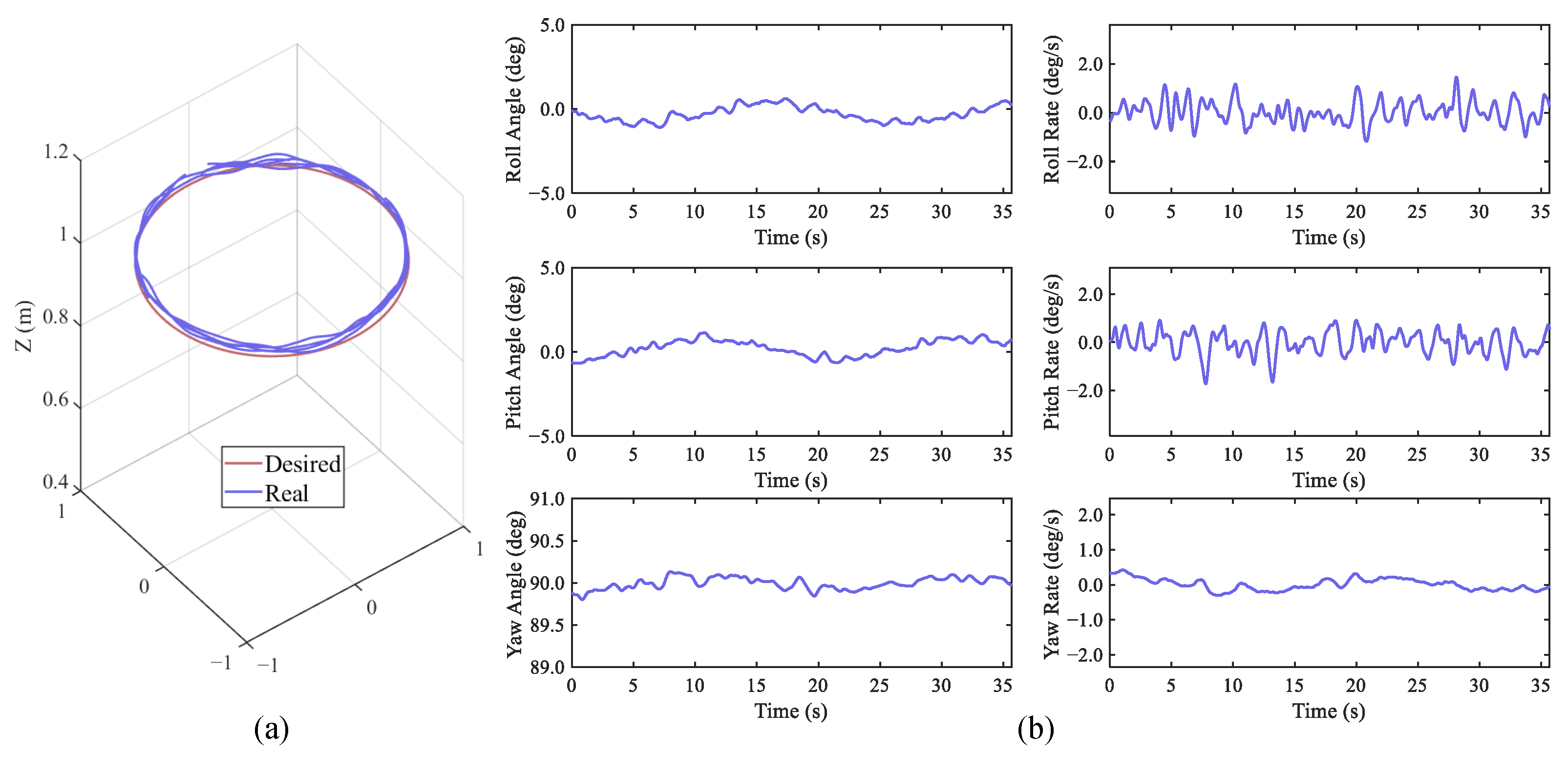
4.3. Simulation and Analysis

To verify the dynamic controllability and motion stability of the proposed robot structure, a PID-based simulation study was conducted in the PX4 flight controller and Gazebo simulation environment. In the simulation, a dual-loop PID controller was employed to independently regulate the position and attitude. Specifically, the outer-loop position controller had proportional gains of $7.0$, $7.0$, and $6.0$ along the three axes, with corresponding velocity gains of $6.0$, $6.0$, and $3.0$. The inner-loop attitude controller had attitude gains of $3.5$, $3.5$, and $0.3$ and angular velocity gains of $0.5$, $0.5$, and $0.1$ for the roll, pitch, and yaw channels, respectively. The MW-LAR model was set with a mass of $2.78$ kg, gravitational acceleration of 9.81 $\mathrm{m}/{\mathrm{s}}^2$, and a rotor arm length of $0.20$ m, while considering the physical constraints of the actuators. Rotor thrust was modeled quadratically, with a thrust coefficient of $7.27\times {10}^{-6}\mathrm{N}/{(\mathrm{rad}/\mathrm{s})}^2$ and a rotor torque coefficient of $0.016$ m. Additionally, the maximum angular velocity of each rotor was limited to 1000 rad/s. At the start of the simulation, the robot’s position, velocity, and attitude were all initialized to zero.

As shown in Figure 9, the robot demonstrates excellent tracking performance in three-dimensional position and velocity, accurately following the desired circular trajectory. Meanwhile, the variations in the roll, pitch, and yaw angles remain small, and the overall motion stays stable. These results indicate that the proposed robot structure possesses good dynamic stability and controllability, thereby confirming the rationality of the structural design and providing theoretical support for subsequent experimental validation.

5. Experiments and Results

To comprehensively evaluate the multi-modal performance of the proposed robot, a prototype integrating an onboard battery was fabricated via 3D printing, with a total mass of 2.5 kg. Based on this prototype, a series of experiments was conducted to validate its locomotion capabilities in both ground and flight modes.

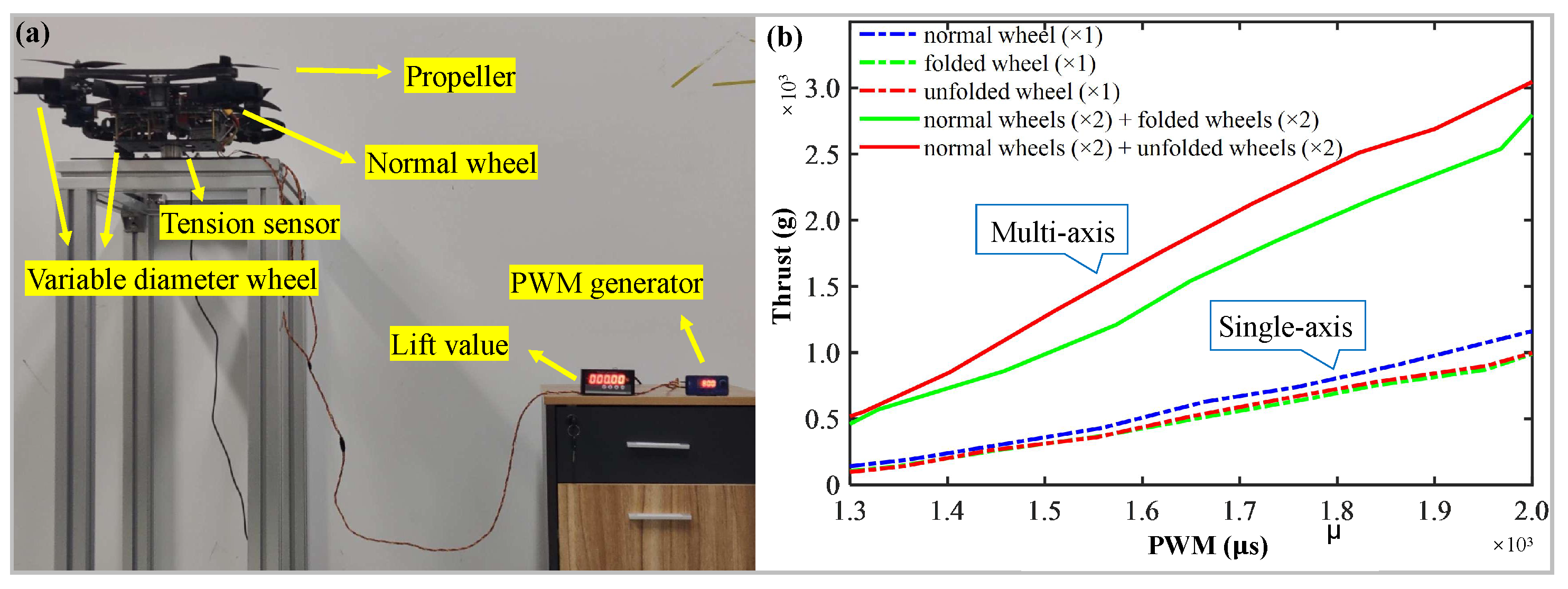
5.1. Investigation on the Influence of Wheels on Propeller Lift

To analyze the aerodynamic influence of the wheel structures added beneath the propellers, two sets of experiments were designed and conducted. The first set aimed to measure the lift variation in a single motor–propeller system under different wheel configurations, while the second set evaluated the total thrust of the complete robot in different morphologies. The experimental setup used for data collection is shown in Figure 10a. In the first set of experiments, the maximum lift of a single motor–propeller unit without wheels was measured to be 1500 g, which served as the baseline. Under the same experimental configuration, the lift was then measured with normal wheels, folded wheels, and unfolded wheels, respectively. The corresponding maximum lifts were 1260 g, 1010 g, and 1020 g, as indicated by the blue, green, and red dashed lines in Figure 10b. Compared with the baseline, the lift losses (LL) caused by the presence of different wheels were calculated as follows: LL_normal = 16%, LL_folded = 32.67%, and LL_unfolded = 32%. In the second set of experiments, the total thrust of the MW-LAR prototype was further tested under two representative configurations: the folded state (two folded wheels + two normal wheels) and the unfolded state (two unfolded wheels + two normal wheels). The results, shown as the green and red solid lines in Figure 10b, indicate that the maximum total thrusts were 2870 g and 3060 g, respectively.

The experimental results indicate that the presence and structural configuration of the wheels have a certain influence on the aerodynamic performance of the propellers. Compared with the lift without wheels, adding normal or variable-diameter wheels will cause lift loss, and the loss induced by variable-diameter wheels is greater than that of normal wheels, but the folding/unfolding process of the variable-diameter wheel is similar, indicating that the current morphing mechanism can maintain relatively stable aerodynamic characteristics during dynamic shape changes. In addition, it can be observed that, under the same PWM (Pulse Width Modulation) signal, the total thrust from the four motors is less than 4 times the single-axis lift. This is mainly due to the increase in the number of propeller motors, the increase in the load on the power system, causing voltage drop, or partly due to the aerodynamic interference between two adjacent propellers.

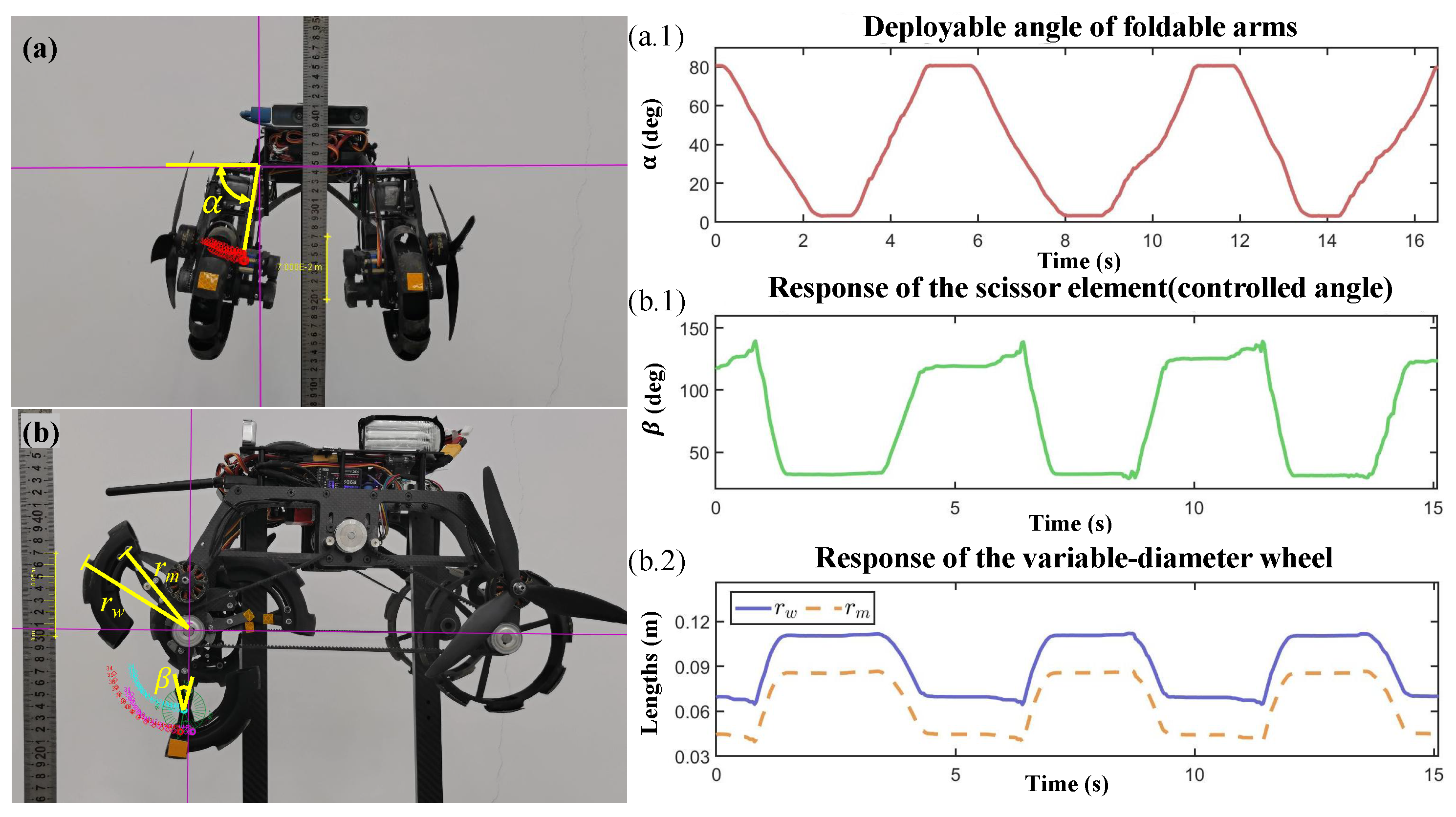
5.2. Performance of Foldable Arms and Morphing Wheels of the MW-LAR

We then conducted experiments to evaluate the performance of the folding arms and variable-diameter wheels, and the experimental setup is shown in Figure 11. In the folding-arm test, the robot was mounted on a fixed platform, and the two folding arms were driven by a set of servomotors with the same PWM input signal to ensure they rotated freely and simultaneously within a specified range. A motion camera was used to track the deployable angle $\alpha$. The results from several repeatable cycles are plotted in Figure 11(a.1), where a range of $[0,{83}^{\circ }]$ is achieved, which is 28% higher than the maximum arm folding angle of 65° for the robot in [26]. In the variable-diameter wheel test, the robot was also fixed to the platform to ensure the wheels could freely change size. A motion camera was used to track the change in the deployable angle $\beta$ of the scissor elements, the length of the morphing mechanism $r_m$ and the wheel’s radius $r_w$. The results in several repeatable cycles are plotted in Figure 11(b.1,b.2), where the length of the morphing mechanism $r_m$ varies from 0.04 m to 0.085 m with $\beta$ changing from $[{32}^{\circ },{139}^{\circ }]$, which is a 67% improvement over the $\beta$, which is $[{49}^{\circ },{113}^{\circ }]$ in the previous version [26], and the maximum morphing ratio of the variable-diameter wheel is 2.1.

5.3. Bench-Top Flight Test of the MW-LAR

To evaluate the controllability of the folding-arm structure in flight mode, experiments were conducted on the robot under two configurations: (i) fully extended arms and (ii) arms folded downward. During the experiments, the robot was mounted on a three-axis stabilized platform that constrained translational motion while allowing rotational degrees of freedom. Reflective markers were attached to key structural components in a motion-capture environment to enable precise measurement of attitude and position, thereby ensuring experimental safety and repeatability. The control system employed a hierarchical PID architecture, in which the inner loop was responsible for attitude stabilization and the outer loop for altitude maintenance.

As shown in Figure 12, the robot takes off at 7 s and reaches a hovering altitude of approximately 0.8 m at around 10 s. The in-air folding process begins at about 14 s, at which point the yaw angle remains stable at approximately 73°, and the arms start folding downward. During the initial stage of folding, the yaw angle temporarily deviates to about 65° at around 16 s, corresponding to a maximum variation of approximately 8°, and reaches a maximum folding angle of about 40° at 19.6 s. As the folding process progresses, the yaw angle gradually recovers and eventually stabilizes at approximately 75°, with the overall variation remaining within about 10°. Throughout the entire folding process, the flight altitude remains nearly constant. Similarly, during the landing phase, a brief yaw fluctuation of about 10° is observed, after which the system returns to a stable state. The angular velocity response exhibits only minor oscillations during the folding and landing phases, while remaining stable during the rest of the flight.

The short-term yaw fluctuations observed above mainly originate from abrupt changes in the system’s moment of inertia caused by structural variations during the in-air folding process, which introduce transient disturbances. It should be noted that in this experiment, the yaw angle was not set as an independent control objective, as its variations have a limited impact on overall attitude stability and flight safety. Meanwhile, the flight altitude remains essentially unchanged throughout the folding process, indicating that the thrust compensation mechanism effectively counteracts the aerodynamic disturbances induced by arm motion. As the folding process concludes, the transient disturbances introduced by structural changes gradually decay, and the system attitude correspondingly returns to a stable state.

5.4. Traversal Performance Tests of the MW-LAR in Ground Mode

To assess the robot’s capabilities in ground mode, we constructed a multi-dimensional validation scenario in the complex terrain of an industrial factory, as shown in Figure 13. Figure 13a presents a typical process of the robot traversing a narrow pipe with a steel structure. Before the 8 cm vertical obstacle, the traditional multi-modal robot is limited by the fixed wheel diameter to climb over the pipe and cannot enter the workspace with a cross-section width of only 32 cm due to the body’s limitations. In contrast, our robot can actively expand the front wheel diameter to 20 cm to cross the obstacle, then contract it back to its base diameter of 13 cm using differential steering to complete a 90° in situ turn, and finally exit the constrained space in a compact form. Figure 13b shows a deep pit crossing experiment with a width of 45 cm. Unlike traditional schemes that require frequent mode switching and incur high energy consumption, our robot extends its folding arms to widen the body and adjusts the wheel-ground contact force dynamically to achieve non-flying obstacle traversal.

Further analysis demonstrates the robot’s significant adaptability in confined spaces: (i) Obstacle-crossing capability: the variable-diameter wheels can adjust from 13 to 20 cm, allowing traversal of obstacles approximately twice the wheel diameter. (ii) Low energy consumption: by dynamically adjusting wheel-ground contact forces, the robot can perform non-flying obstacle crossing, reducing energy consumption by about 98% compared with flight-based crossing. (iii) Narrow-space traversal: by adjusting the structure through folding arms, the robot can pass through confined spaces, demonstrating high adaptability to complex environments.

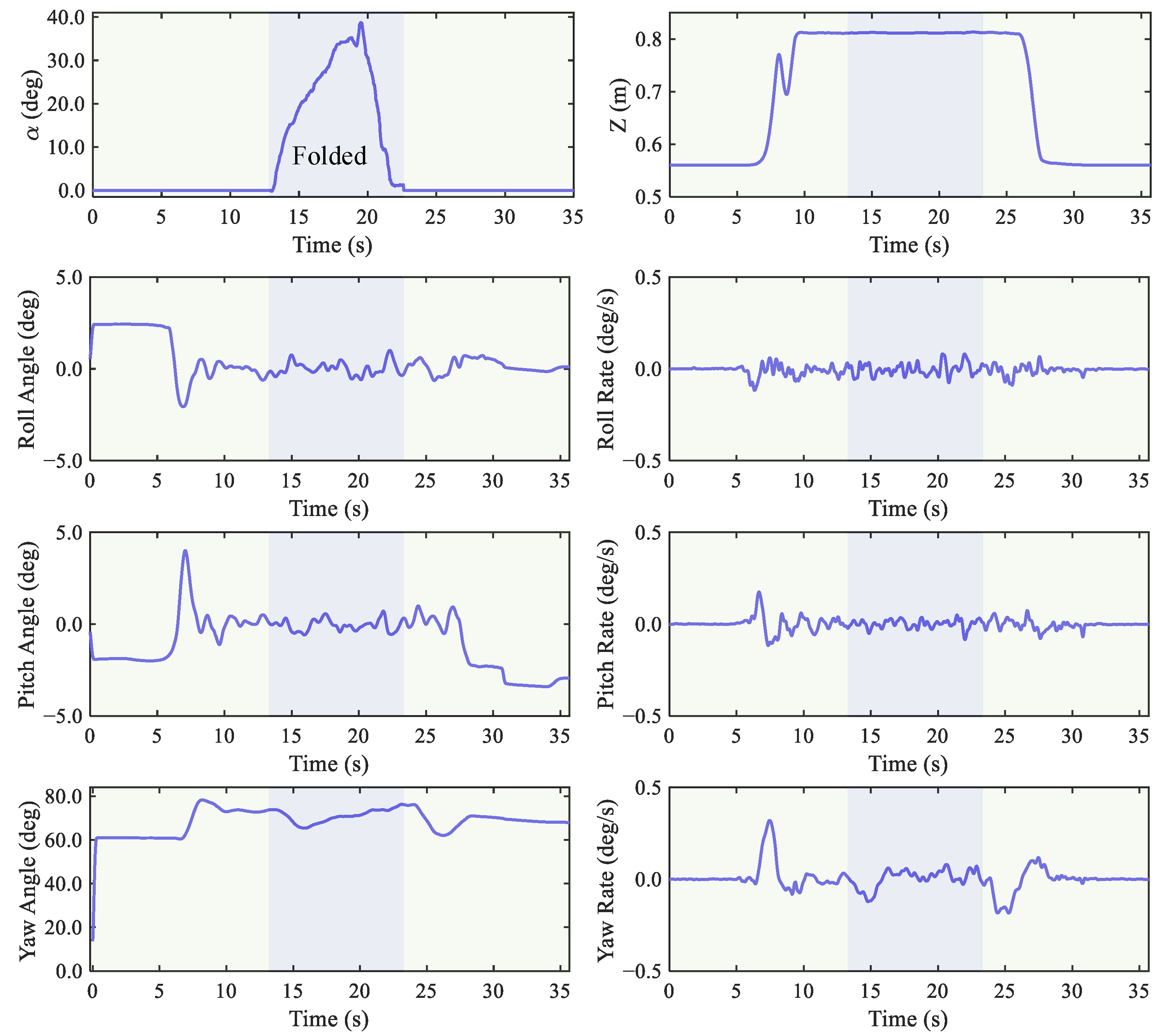
5.5. In-Flight Morphing Performance Tests of the MW-LAR

To evaluate the robot’s dynamic morphing performance in flight mode and verify the feasibility of landing in a configuration close to the ground mode, an outdoor flight experiment was conducted. The experimental procedure and data are shown in Figure 14a–d. During the experiment, the robot vertically took off with a preset arm folding angle of $\alpha ={45}^{\circ }$ and maintained the folded state during the liftoff phase. At 52 s, the arm began to unfold, rapidly reaching the standard quadrotor shape within $0.5$ s. The robot entered the landing phase at 11 s, during which it executed the folding command synchronously, and achieved a precise touchdown with a maximal folding angle of $\alpha ={83}^{\circ }$ at 13 s.

Figure 14e presents the evolution of the full-flow flight parameters. The results show that the RMSE of the pitch angle and the roll angle are $1.6^{\circ }$ and $2.5^{\circ }$, respectively, both within the acceptable range of deviation from the preset control commands. The altitude trajectory also remains generally stable. It should be noted that the instantaneous fluctuation of the attitude angle during the two configuration transitions (unfolding/folding) is controlled within $5^{\circ }$, and the robot is able to return to a stable state within $0.8$ s.

The experimental results show that the robot can complete two aerial configuration transitions within a 15-s flight period ($0.5$ s for unfolding and $1.2$ s for folding) while maintaining good attitude stability throughout the process. Moreover, it is capable of landing in a posture close to the ground mode. This provides new ideas for the application of heterogeneous robots in unstructured environments (e.g., jungle rescue), dynamic take-off and landing scenarios (mobile platform landing), and flight missions in confined spaces, which significantly expand the mission boundaries of quadrotor systems.

Through the above five sets of experiments, the robot’s overall performance in terms of aerodynamic characteristics, structural morphing, ground locomotion, and flight control was systematically verified. The results demonstrate that the proposed transformable ground–aerial amphibious robot can maintain stable motion and control performance under different configurations, achieving smooth transitions between flight and ground modes. This indicates strong environmental adaptability and task execution capability.

6. Conclusions

This paper presents an enhanced ground mobile robot, the Morphing Wheeled Land–Air Robot (MW-LAR). Unlike traditional wheeled robots that are limited by fixed structures, the robot can not only move efficiently on the ground but also actively adjust its wheel diameter according to terrain conditions and perform aerial transitions when necessary. Specifically, the MW-LAR is equipped with variable-diameter wheels that can flexibly adjust their size according to terrain variations, thereby enhancing its obstacle-surmounting capability in ground mode. In addition, a pair of foldable arms enables rapid transitions between flight and ground modes as well as dynamic morphing during flight, achieving a minimum folding time of $0.9$ s and a maximum folding angle of ${83}^{\circ }$. The experimental results demonstrate that the MW-LAR exhibits high flexibility and environmental adaptability in complex environments. In the ground mode, the robot can overcome obstacles by enlarging its wheel radius, thereby avoiding unnecessary takeoffs. In the flight mode, it can achieve stable mode transitions and perform in-air transformations through arm folding, while also being capable of safely landing in a posture close to the ground mode. Future work will focus on integrating additional sensors for autonomous decision-making, such as path planning and self-attitude adjustment, and further evaluating the robot’s dynamic performance under model predictive control.