Insecticidal Activity Evaluation of Phenylazo and Dihydropyrrole-Fused Neonicotinoids Against Cowpea Aphids Using the MLR Approach ^†

Abstract

This paper presents a Quantitative Structure-Activity Relationship (QSAR) study of a series of 24 dihydropyrrole-fused and phenylazo neonicotinoid derivatives, with insecticidal activity tested against Cowpea aphids (Aphis craccivora). In this regard, the conformational search ability of the OMEGA software was employed to model neonicotinoid conformer ensembles, using molecular mechanics calculations based on the 94s variant of the Merck Molecular force field (MMFF94). The minimum energy conformers were used to calculate structural descriptors, which were further related to the insecticidal activity (pLC₅₀ values), using the multiple linear regression (MLR) approach. The genetic algorithm was used for variable selection and several criteria for internal and external model validation. A robust model (r² = 0.880, r²_adj = 0.855, q²_LOO = 0.827, s = 0.2098, F = 34.295) with predictive power (concordance correlation coefficient (CCC)_ext = 0.945, r²_m= 0.824) was obtained, using the QSARINS software. The developed model can be confidently used for the prediction of the insecticidal activity of new chemicals, saving a substantial amount of time and money.

1. Introduction

Neonicotinoids are considered to be one of the most important and relevant classes of insecticides used nowadays [1,2]. Neonicotinoids are synthetic insecticides acting on the insect nicotinic acetylcholine receptor (nAChR) and have been increasingly used to control various insects during recent decades, especially since imidacloprid was introduced to the market [3]. However, the neonicotinoids success is being provoked by the rapid development of resistance [2] and severe bee toxicity [4,5,6]. It is considered that neonicotinoid insecticides represent the most effective chemical class for the control of sucking insect pests (aphids, whiteflies, leaf- and planthoppers, thrips), micro lepidoptera, and a number of coleopteran pest species [7]. Neonicotinoids have the advantage of their plant systemicity over other insecticides. After application into the soil or the seed, these compounds are absorbed through the plant roots, where they are distributed and give therefore consistent and long-lasting control of sucking insects.

The coplanar segment between guanidine or amidine and pharmacophore in the neonicotinoids could create an electronic conjugation to facilitate the partial negative charge flow toward the tip atom and increase the binding affinity to the insect target [8]. Photostabilized compounds selective for insects relative to mammals have photolabile nithiazine with a nitromethylene moiety and no cationic substituent [9].

Quantitative Structure-Activity Relationship (QSAR) is the most commonly used method to understand how chemical structure features correlate with the toxicity of natural and/or synthetic chemicals like insecticides. This method offers the possibility of searching for new insecticides with enhanced activity against insects and pests. The urgent need for the development of a new insecticide is related to the phenomenon of insecticide-resistant cases of pests. In this regard, several computational approaches were applied to study the insecticidal activity of neonicotinoids [10,11,12,13,14,15].

In this study, the QSAR model of 24 dihydropyrrole-fused and phenylazo neonicotinoid derivatives is derived from the data set of chemical structures and insecticidal activities tested against Cowpea aphids (Aphis craccivora) using multiple linear regression (MLR) approach.

Molecular mechanics calculations, using the 94s variant of the Merck Molecular force field (MMFF94), were used to model the neonicotinoid structures. Statistical analysis using several criteria was employed to find a robust and predictive MLR model. The best derived MLR model could be confidently used to predict the insecticidal activity of newly designed insecticides.

2. Methods

2.1. Dataset and Theoretical Molecular Descriptors Calculation

A dataset of 24 phenylazo and dihydropyrrole-fused neonicotinoid derivatives (

Table 1. Experimental (pLC_50exp) and predicted for the best multiple linear regression (MLR) model (pLC_50pred) insecticidal activity values of neonicotinoids.

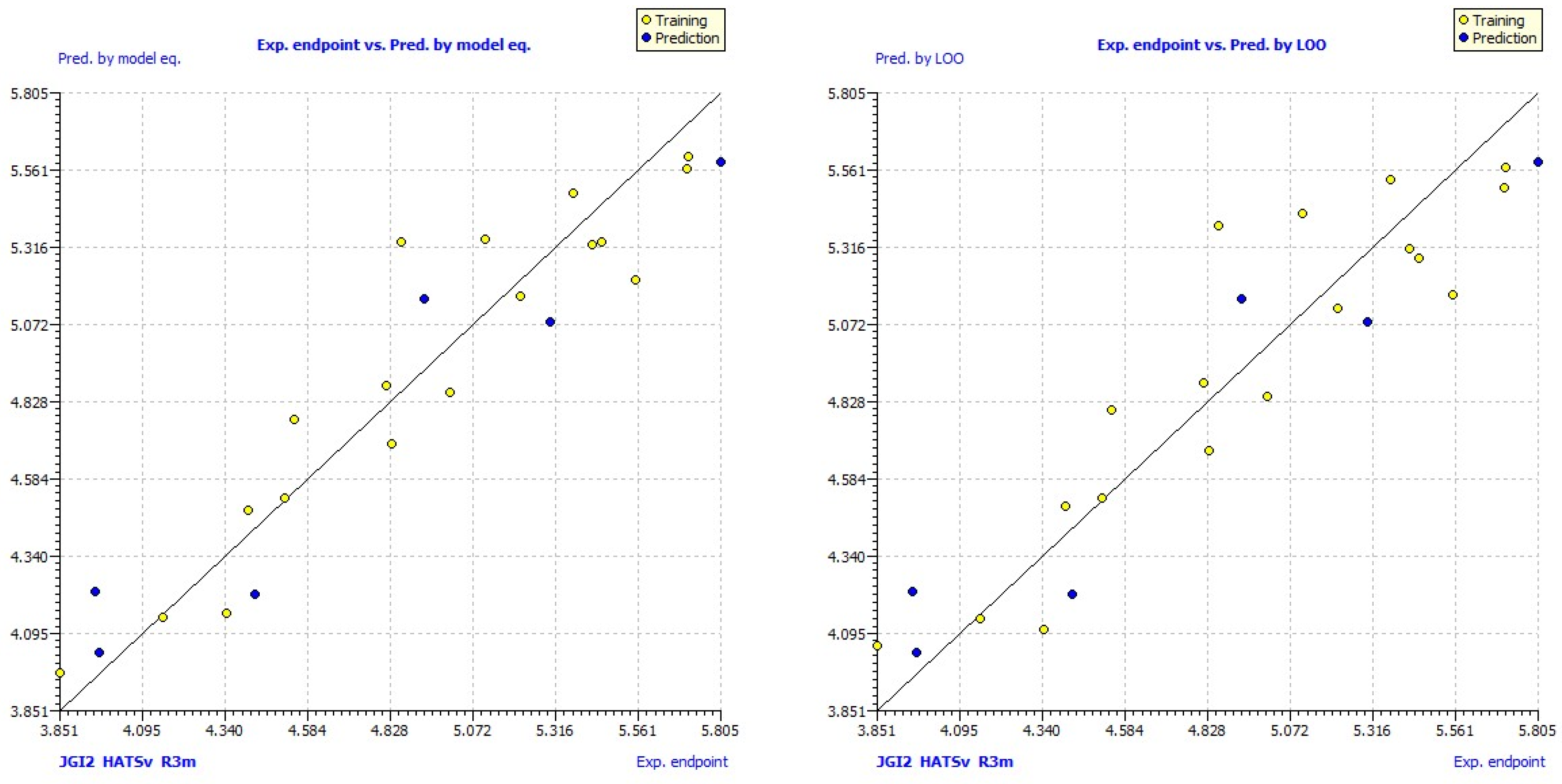
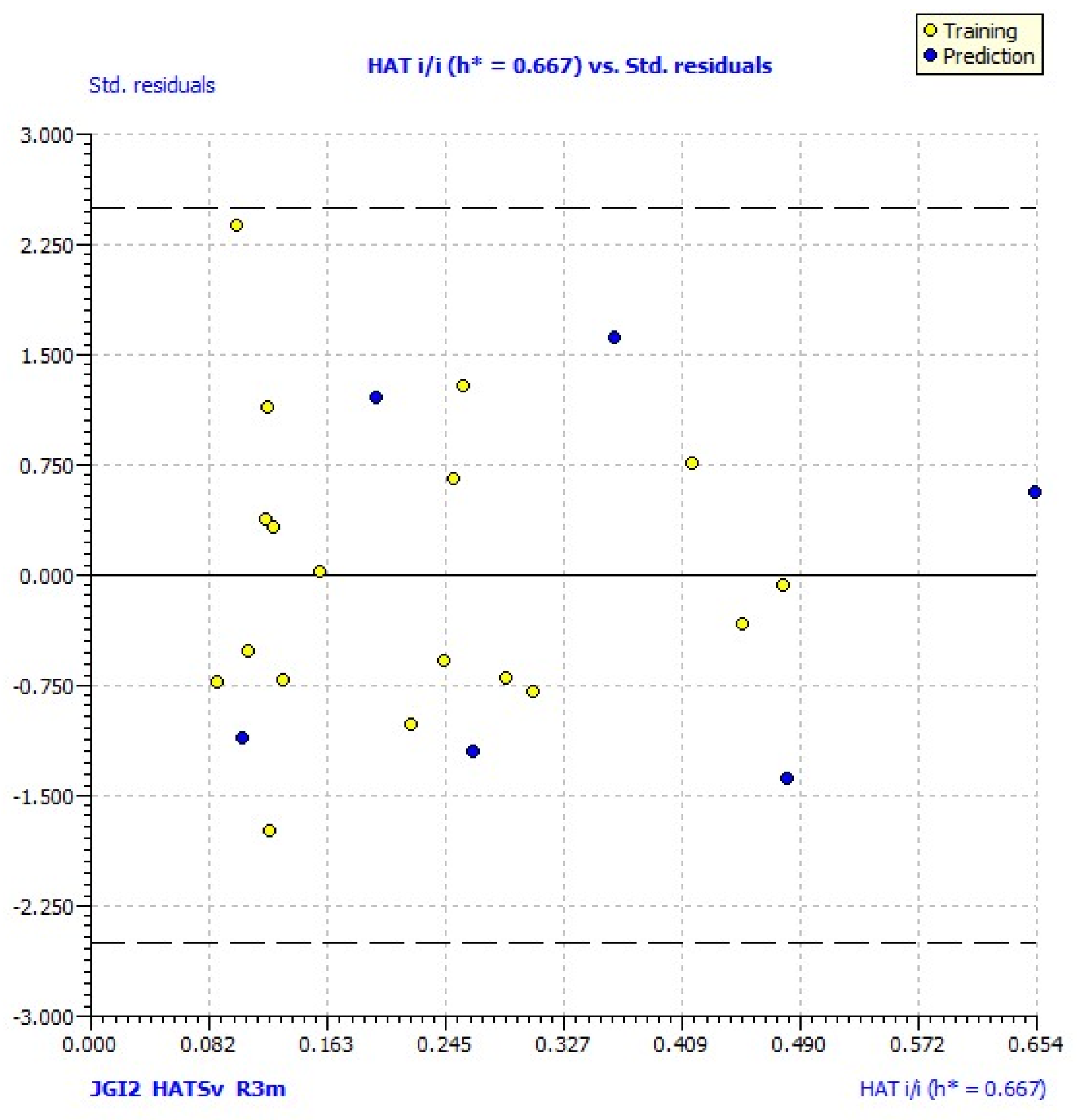
No	Structure	pLC50exp	pLC50pred	No	Structure	pLC50exp	pLC50pred
1		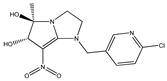5.21	5.16	13 *		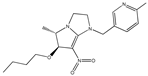3.97	4.04
2		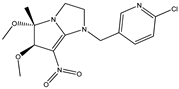5.70	5.57	14 *		4.43	4.22
3*		5.80	5.59	15		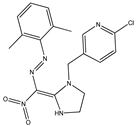5.37	5.49
4		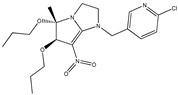5.71	5.61	16 *		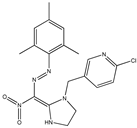5.30	5.08
5		5.11	5.34	17		5.43	5.33
6		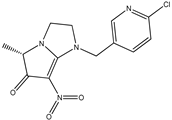3.85	3.97	18		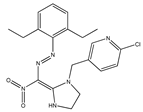5.55	5.21
7		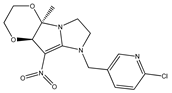4.55	4.77	19		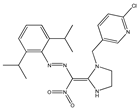4.86	5.34
8		4.52	4.53	20		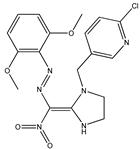5.00	4.86
9		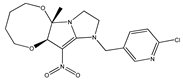4.41	4.49	21		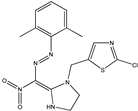5.46	5.33
10		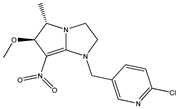4.35	4.16	22		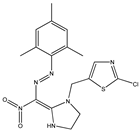4.82	4.88
11*		3.96	4.23	23*		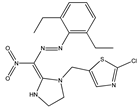4.93	5.16
12		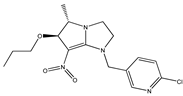4.16	4.15	24		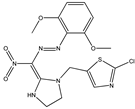4.83	4.70

* Test compounds included in the best MLR model.

) having the insecticidal activity (LC₅₀, in mmol/L) against cowpea aphids (Aphis craccivora) [16,17] was analyzed. pLC₅₀ values were used as the dependent variable.

The neonicotinoid structures were pre-optimized using the MMFF94 molecular mechanics force field included in the Omega (Omega v.2.5.1.4, OpenEye Scientific Software, Santa Fe, NM) software [18,19]. For conformer generation, the maximum number of conformers per compound set of 400 and a root-mean-square deviation (RMSD) value of 0.5 Å were employed during the conformer ensemble generation.

The conformers of minimum energy were then used to calculate the structural parameters, using the DRAGON (Dragon Professional 5.5, 2007, Talete S.R.L., Milano, Italy) and InstanJChem (Instant JChem (2012) version 5.10.0, Chemaxon) software.

2.2. The Multiple Linear Regression Method

The MLR approach [20] was employed to relate the pLC₅₀ values with the calculated structural descriptors, using the QSARINS v. 2.2 program [21,22]. The genetic algorithm with leave-one-out cross-validation correlation coefficient was used for variable selection of a constrained function to be optimized, a mutation rate of 20%, and a population size with 10 and 500 iterations.

2.3. Model Validation

The dataset was divided randomly into training and test (25% of the total number of compounds) sets. Following compounds: 3, 11, 13, 14, 17, and 23 were included in the test set (Table 1).

Several criteria were used for testing the predictive model power: ${\mathrm{Q}}_{\mathrm{F}1}^2$ [23], ${\mathrm{Q}}_{\mathrm{F}2}^2$ [24], ${\mathrm{Q}}_{\mathrm{F}3}^2$ [25], the concordance correlation coefficient (CCC) [26] (having the thresholds values higher than 0.85, [27]) and the predictive parameter ${\mathrm{r}}_{\mathrm{m}}^2$ (with a lowest threshold value of 0.5) [28].

The model overfit was checked using the Y-randomization test [29] and by comparing the root-mean-square errors (RMSE) and the mean absolute error (MAE) of the training and validation sets [30].

Y-scrambling [31], the adjusted correlation coefficient (${\mathrm{r}}_{\mathrm{a}\mathrm{d}\mathrm{j}}^2$), and q² (leave-one-out, ${\mathrm{q}}_{\mathrm{L}\mathrm{O}\mathrm{O}}^2$, and leave-more-out, ${\mathrm{q}}_{\mathrm{L}\mathrm{M}\mathrm{O}}^2$) cross-validation coefficients were employed for internal model validation.

The Multi-Criteria Decision Making (MCDM) validation criterion [32] is used to summarize the performance of MLR models. For every validation criterion, a desirability function was associated, and MCDM had values between 0 (the worst) and 1 (the best).

3. Results and Discussion

The autoscaling method was employed for normalizing the data:

$$\mathrm{X}{\mathrm{T}}_{\mathrm{m}\mathrm{j}}=\frac{{\mathrm{X}}_{\mathrm{m}\mathrm{j}}-{\overline{\mathrm{X}}}_{\mathrm{m}}}{{\mathrm{S}}_{\mathrm{m}}}$$

(1)

where for each variable m, XT_mj, and X_mj are the j values for the m variable after and before scaling, respectively. ${\overline{\mathrm{X}}}_{\mathrm{m}}$ is the mean and S_m is the standard deviation of the variable.

The variables contained in the MLR models were selected using the genetic algorithm. The statistical (fitting and predictivity) results are included in

Table 2. Fitting and cross-validation statistical results of the MLR models *.

Model	${\mathbf{r}}_{\mathbf{t}\mathbf{r}\mathbf{a}\mathbf{i}\mathbf{n}\mathbf{i}\mathbf{n}\mathbf{g}}^2$	${\mathbf{q}}_{\mathbf{L}\mathbf{O}\mathbf{O}}^2$	${\mathbf{q}}_{\mathbf{L}\mathbf{M}\mathbf{O}}^2$	${\mathbf{r}}_{\mathbf{a}\mathbf{d}\mathbf{j}}^2$	RMSEtr	MAEtr	CCCtr	${\mathbf{r}}_{\mathbf{s}\mathbf{c}\mathbf{r}}^2$	${\mathbf{q}}_{\mathbf{s}\mathbf{c}\mathbf{r}}^2$	SEE	F
MLR1	0.880	0.827	0.806	0.855	0.185	0.147	0.936	0.176	−0.404	0.210	34.295
MLR2	0.865	0.793	0.774	0.837	0.196	0.164	0.928	0.174	−0.396	0.222	30.000
MLR3	0.854	0.777	0.755	0.822	0.205	0.172	0.921	0.178	−0.390	0.232	27.208
MLR4	0.854	0.790	0.772	0.823	0.204	0.161	0.921	0.177	−0.397	0.232	27.333

* ${\mathrm{r}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{n}\mathrm{g}}^2$: correlation coefficient; ${\mathrm{q}}_{\mathrm{L}\mathrm{O}\mathrm{O}}^2$ leave-one-out correlation coefficient; ${\mathrm{q}}_{\mathrm{L}\mathrm{M}\mathrm{O}}^2$; leave-more-out correlation coefficient; ${\mathrm{r}}_{\mathrm{a}\mathrm{d}\mathrm{j}}^2$; adjusted correlation coefficient; RMSE_tr: root-mean-square errors; MAE_tr: mean absolute error; CCC_tr: the concordance correlation coefficient; ${\mathrm{r}}_{\mathrm{s}\mathrm{c}\mathrm{r}}^2$ and ${\mathrm{q}}_{\mathrm{s}\mathrm{c}\mathrm{r}}^2$: Yscrambling parameters; SEE: standard error of estimates; F: Fischer test.

,

Table 3. The model predictivity results *.

Model	${\mathbf{Q}}_{\mathbf{F}1}^2$	${\mathbf{Q}}_{\mathbf{F}2}^2$	${\mathbf{Q}}_{\mathbf{F}3}^2$	RMSEext	MAEext	CCCext
MLR1	0.904	0.844	0.945	0.211	0.202	0.945
MLR2	0.801	0.676	0.889	0.304	0.293	0.889
MLR3	0.818	0.704	0.896	0.291	0.281	0.896
MLR4	0.744	0.583	0.858	0.345	0.309	0.858

* ${\mathrm{Q}}_{\mathrm{F}1}^2$; ${\mathrm{Q}}_{\mathrm{F}2}^2$;${\mathrm{Q}}_{\mathrm{F}3}^2$: external validation parameters; RMSE_ext: root-mean-square errors; MAE_ext: mean absolute error; CCC_ext: the concordance correlation coefficient.

and

Table 4. The ‘Multi-Criteria Decision Making (MCDM) all’ score values, ${\mathrm{r}}_{\mathrm{m}}^2$ predictivity parameter, and descriptors included in the MLR models *.

Model	${\mathbf{r}}_{\mathbf{m}}^2$	MCDM all	Descriptors included in the MLR model *
MLR1	0.824	0.867	JGI2 HATSv R3m
MLR2	0.795	0.814	BEHp2 JGI2 R3m
MLR3	0.791	0.812	JGI2 Mor06m R3m
MLR4	0.720	0.786	JGI2 R3m R8m+

* JGI2: mean topological charge index of order2 (Galvez topological charge index); HATSv: leverage-weighted total index/weighted by atomic van der Waals volumes (GETAWAY descriptor); R3m: R autocorrelation of lag 3/weighted by atomic masses (GETAWAY descriptor); BEHp2: highest eigenvalue n. 2 of Burden matrix/weighted by atomic polarizabilities (BCUT descriptor); Mor06m: 3D-MoRSE—signal 06/weighted by atomic masses (3D-MoRSE descriptor); R8m+: R maximal autocorrelation of lag 8/weighted by atomic masses (GETAWAY descriptor).

.

The ‘MCDM all’ scores, based on the fitting, cross-validated, and external criteria were considered for choosing the best MLR models.

For the reliability of the best MLR1 model, the experimental versus predicted pLC₅₀ values and Y-scramble plots are presented in Figure 1 and Figure 2, respectively.

In the Y-scrambling test performed for the MLR models, a significant low scrambled r² (${\mathrm{r}}_{\mathrm{s}\mathrm{c}\mathrm{r}}^2$) and cross-validated q² (${\mathrm{q}}_{\mathrm{s}\mathrm{c}\mathrm{r}}^2$) values were obtained for 2000 trials. Figure 2 shows that in case of all the randomized models; the values of ${\mathrm{r}}_{\mathrm{s}\mathrm{c}\mathrm{r}}^2$ and ${\mathrm{q}}_{\mathrm{s}\mathrm{c}\mathrm{r}}^2$ for the MLR1 model were <0.5 (${\mathrm{r}}_{\mathrm{s}\mathrm{c}\mathrm{r}}^2$/${\mathrm{q}}_{\mathrm{s}\mathrm{c}\mathrm{r}}^2$ of 0.1759/-0.4035). The low calculated ${\mathrm{r}}_{\mathrm{s}\mathrm{c}\mathrm{r}}^2$ and ${\mathrm{q}}_{\mathrm{s}\mathrm{c}\mathrm{r}}^2$ values indicate no chance correlation for all MLR chosen models (Table 2).

The Williams plot (standardized residuals versus leverages, with the leverage threshold h* = 0.667 for the MLR1 model), in the range of ±2.5σ, was used to verify the domain applicability. All compounds in the dataset are within the applicability domain of the MLR1 model, as presented in Figure 3.

The selected descriptors included in the MLR1 best model are not intercorrelated, as presented in the correlation matrix from

Table 5. Correlation matrix of the descriptors included in the best MLR1 model and their standardized coefficients (Std. coeff.).

	JGI2	HATSv	R3m	Std. coeff.
JGI2	1			0.967
HATSv	−0.278	1		0.321
R3m	−0.121	0.623	1	−0.617

.

Good correlations with the insecticidal activity and predictive model power were notices for all MLR models. Model MLR4 was less predictive (in accordance to its ${\mathrm{Q}}_{\mathrm{F}2}^2$ value) compared to the other MLR models. Closer values of the RMSE and the MAE of the training and validation sets were observed for the MLR2, MLR3, and MLR4 models. MLR1 model was considered being the best one according to several other statistical parameters of fitting and the ‘MCDM all’ score values.

The best MLR1 model had three descriptors: one Galvez topological charge index (JGI2, which means the topological charge index of order 2) and two GETAWAY descriptors (HATSv, which represents the leverage-weighted total index/weighted by atomic van der Waals volumes and R3m—R autocorrelation of lag 3/weighted by atomic masses). The increase of the JGI2 and HATSv descriptor values is favorable for high insecticidal activity. Lower values of R3m raise the insecticidal activity.

New neonicotinoid structures with insecticidal activity against the cowpea aphids can be designed based on the MLR models presented in this study.

4. Conclusions

Quantitative structure-insecticidal activity relationships were developed using the multiple linear regression approach for neonicotinoids with dihydropyrrole-fused and phenylazo moieties, active against the cowpea aphids (Aphis craccivora). Insecticide structures were modeled using the MMFF94s force field. Descriptors of the minimum conformers were related to the pLC₅₀ values using the multiple linear regression approach. Good correlations and predictive models were obtained. Getaway and Galvez topological charge index descriptors included in the best MLR model can be used for prediction of new insecticides active against the cowpea aphids, saving experimental time and money.