Vibration Emissions of Grinders: Experiments and a Model ^†

Abstract

A simple two-rigid-body model of an electrical grinder was created to calculate the vibration emissions according to the test code EN 60745-2-3. The model assumes that the operator does not affect the vibration emissions. Experiments with and without the operator validated this hypothesis and demonstrated the model’s abilities and limitations.

1. Introduction

Electric grinders are vibrating tools that are likely to expose operators to vibration levels higher than the values defined by the European directive. To help companies to choose machines with fewer vibrations, manufacturers are required to declare the vibration emissions. The vibration emissions constitute the frequency-weighted root-mean-square acceleration $a_{hv}$ defined by the standard ISO 5349-1 [1] (typically between 3 and 8 m/s² [2,3,4,5,6] for grinders), measured in accordance with the standard test code EN 60745-2-3. The objective of this study was to develop and verify a simple model which calculates the accelerations of a grinder during standard tests. This model assumes that holding the grinder has no effect on vibration [7,8]. To validate this hypothesis, in addition to standard tests during which an operator holds the grinder, tests without the operator were carried out. Finally, the measured accelerations were compared to those calculated by the model.

2. Materials and Methods

According to the standard EN 60745-2-3 [9], the disks were created from aluminum and perforated in such a way as to create the given imbalance. A thin steel cable was passed through a pulley and attached to the grinder and a mass so as to apply an upwards force and to relieve the weight of the grinder. The grinder was held by an operator and when the grinder was running, the disk spun freely without grinding or cutting any material. Three operators handled the grinders successively and repeated the tests. Other tests were carried out without an operator, and the grinder was simply hung from a long and rigid 1930 N/m tension spring.

The tested grinder was a Metabo W12-125 Quick (Nürtingen, Germany). This is a small grinder weighing 2.4 kg with 125 mm diameter disks. The grinder was tested without the side handle.

For the tests, the accelerations were measured using at least three PCB 356B21 glued triaxle piezoelectric accelerometers. The tension signals of the accelerometers were numerically recorded using a Dewesoft R2DB (Trbovlje, Slovenia) at a frequency of 20,000 Hz. Before the tests, the respective positions of the accelerometers were measured through a 3D scan of the instrumented grinders.

3. Numerical Model

A numerical model was developed considering the perforated disk and the grinder as two rigid bodies linked by a revolute joint. A constant rotational speed $\omega$ between them was assumed.

The main hypothesis of this model was the lack of external force acting on the grinders. Finally, the dynamic equations provided a system of six equations and six degrees of freedom (position of the grinder in the space, including the vector of angular velocity, denoted as $\overrightarrow{\mathsf{\Omega }}$). The system was simplified by neglecting the second-order terms in the angular velocity ($~{ \mathsf{\Omega }}^2$) and other terms through the comparison of the numerical values of mass parameters. Lastly, the complex amplitude vector of the first harmonic (at the rotation frequency) of the steady-state acceleration of point $M$ on the running grinder was given by the two following equations:

$${\overrightarrow{a}}_M=\frac{\mathrm{bal}}{m_T}{\omega }^2{\overrightarrow{e}}_r+j\omega \overrightarrow{\mathsf{\Omega }}\wedge \left(\overrightarrow{CM}-\frac{m_G}{m_T}\overrightarrow{C{G}_{woD}}\right)$$

(1)

$${\stackrel{=}{I}}_T\overrightarrow{\mathsf{\Omega }}=j\omega m_G\frac{\mathrm{bal}}{m_T}\overrightarrow{C{G}_{woD}}\wedge {\overrightarrow{e}}_r$$

(2)

In these equations, bal is the imbalance of the perforated disk, $m_T$ is the total mass of the system, ${\overrightarrow{e}}_r$ is the rotating vector in the plane of the disk, $j=\sqrt{-1}$, $C$ is the center of the disk, $m_G$ is the mass of the grinder without the disk, $G_{woD}$ is the center of mass of the grinder without the disk, and ${\stackrel{=}{I}}_T$ is the sum of the inertia tensor of rigid bodies expressed at their center of mass. All model parameters were known and provided by the manufacturer based on their detailed CAD.

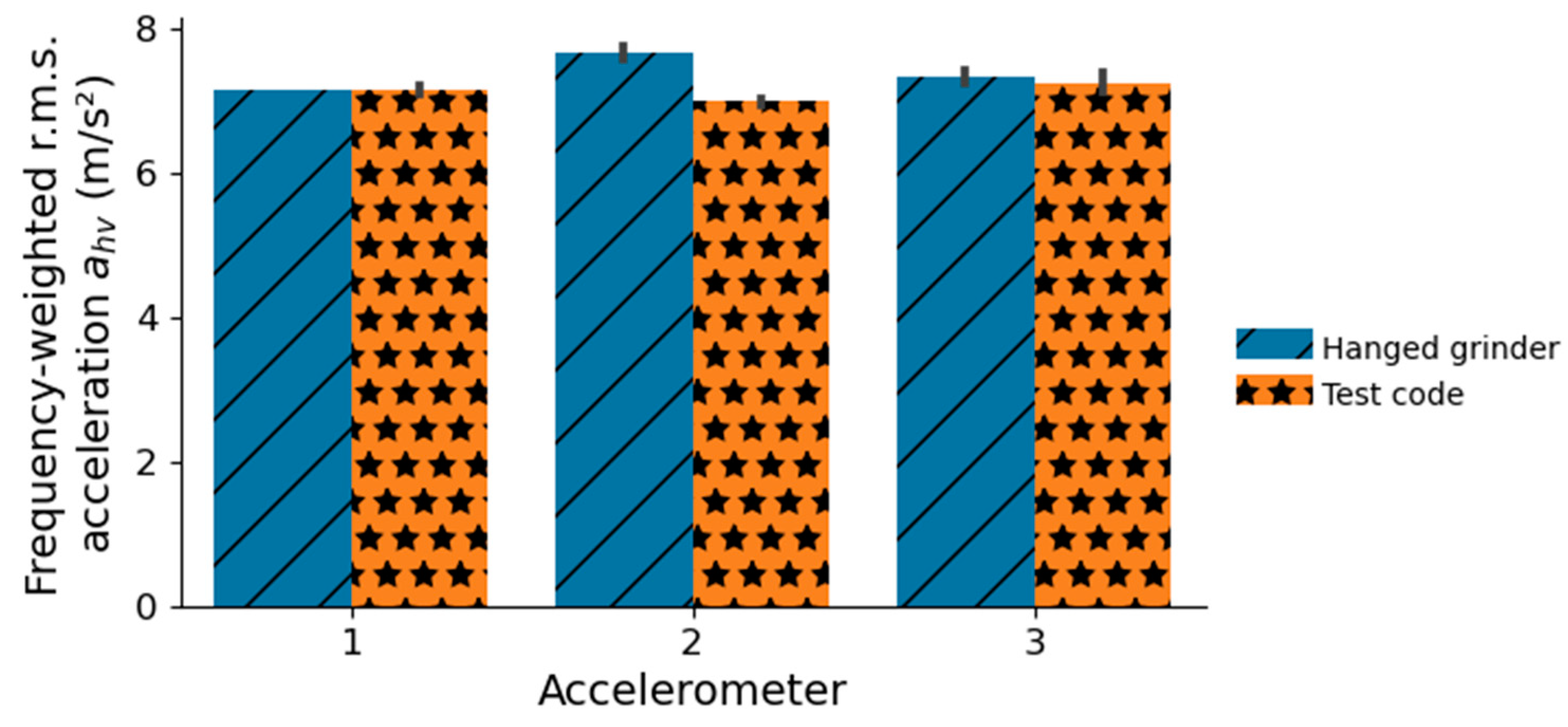
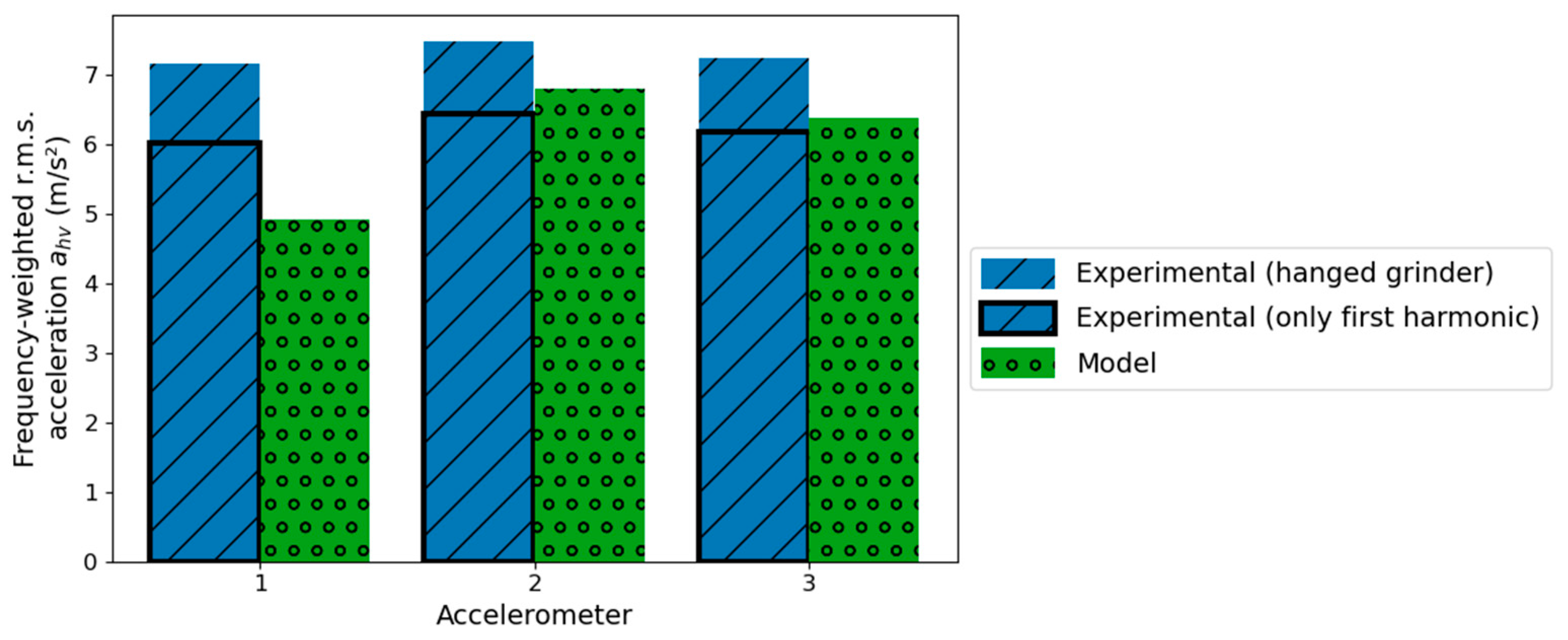
4. Results

Firstly, the frequency-weighted root-mean-square accelerations $a_{hv}$ defined in the standard ISO 5349-1 and implemented during the use of the test codes and tests with the hanging grinder are shown in Figure 1. The accelerations $a_{hv}$ were very close, regardless of whether the grinder was hanging or held by an operator. The low standard deviation values for the test code confirm that handling had no effect on the vibrations. One of the hypotheses regarding the model was therefore valid for this grinder.

Secondly, the amplitude vector of the first harmonic regarding the acceleration was calculated based on the location of the accelerometers. This acceleration was compared to the experimental acceleration obtained with the hanging grinder, as shown in Figure 2.

5. Discussion

The tests described above were conducted using a grinder without a flexible part. In addition, similar tests were carried out using a Bosch GWS 24-230 LVI grinder (Gerlingen, Germany) with both handles being flexible (vibration reduction system). This second grinder was large, weighing 5.5 kg with 230 mm diameter disks. The comparisons of the measured frequency-weighted root-mean-square accelerations $a_{hv}$ in the two tests with (test code) and without an operator (hanging grinder) are shown in Figure 3. The vibrations were not linked to whether an operator was holding the grinder or not, except for the rear handle, which is flexible. The results show that a flexible rear handle reduces vibration exposure, as expected. The model did not account for the flexibility of the grinder parts, and therefore, it cannot be used to calculate the correct acceleration on the flexible handle. However, it could replace the test without an operator to evaluate the effect of the flexible part and could aid in the design of the flexible part.

6. Conclusions

Comparing the vibration $a_{hv}$ on a hanging grinder to that obtained according to the test code EN 60745-2-3, no difference was observed. Thus, for this type of grinder, there is no need to consider the operator’s hand in order to model and predict the vibration emissions of grinders. A simple two-rigid-body model was developed and allowed us to calculate this vibration value, as declared by the manufacturer. This model cannot be applied to grinders containing flexible parts.