Factoring Muscle Activation and Anisotropy in Modelling Hand-Transmitted Vibrations: A Preliminary Study †
Abstract
1. Introduction
2. Materials and Methods
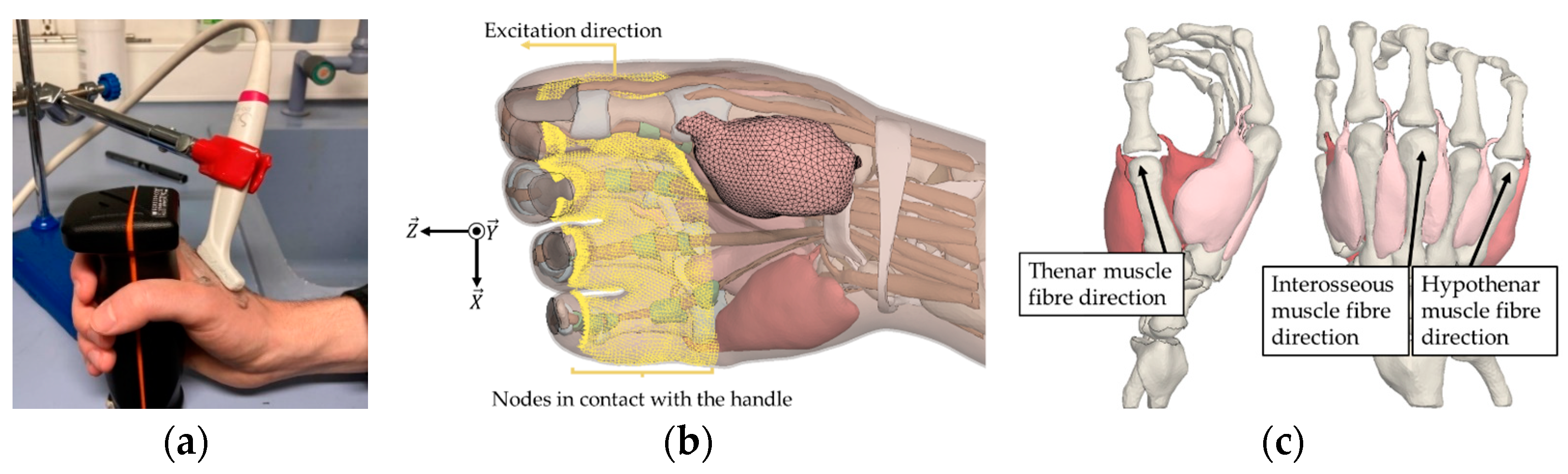
2.1. Measurement of Muscle Elasticity with Supersonic Shear Imagining
2.2. FE Modelling of Hand-Transmitted Vibrations
3. Results
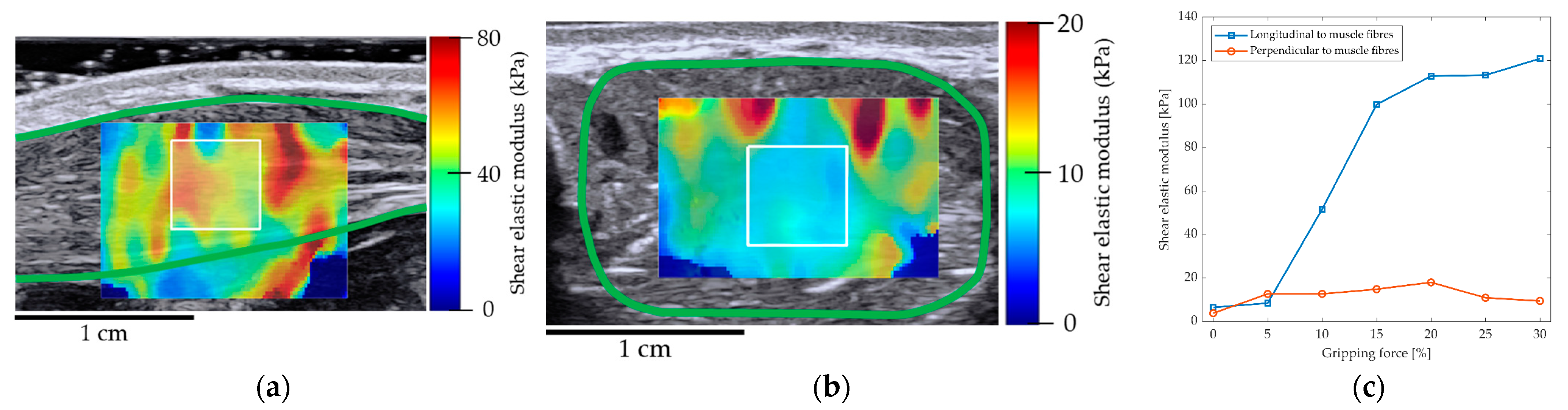
3.1. Effects of Gripping Force on Muscle Elasticity and Fibre Anisotropy
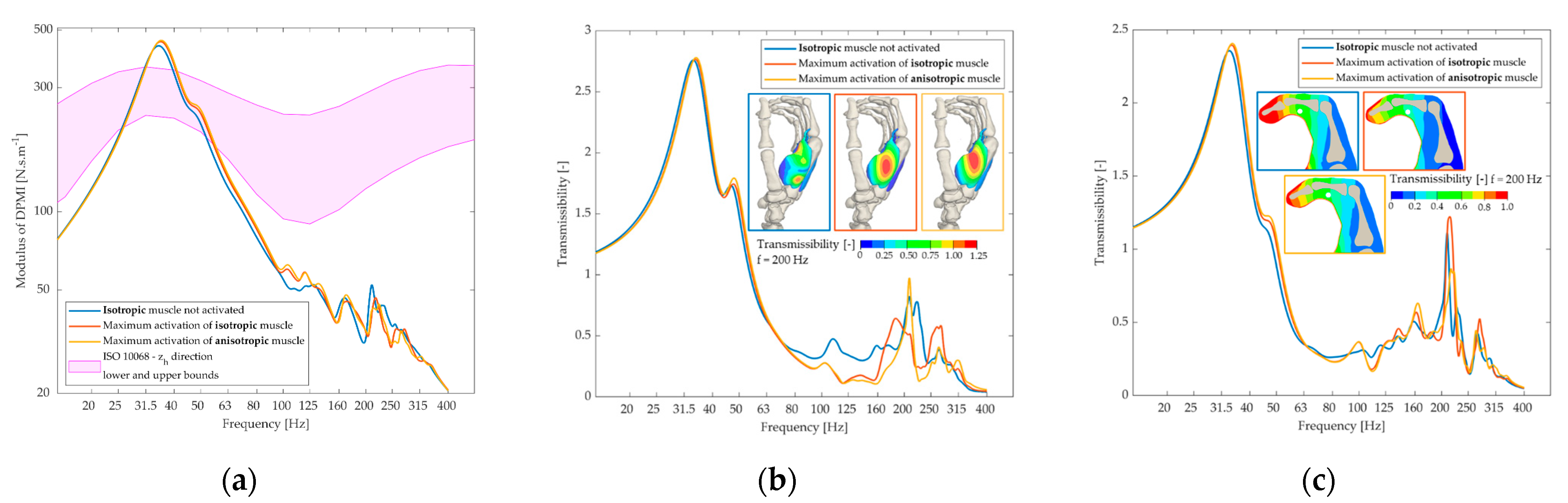
3.2. Effects of Muscle Activation on DPMI and Local Transmissibility
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- FD CR 12349:1996; Mechanical Vibration-Guide to the Health Effects of Vibration on the Human Body. AFNOR: Paris, France, 1996.
- NF EN ISO 5349-1:2001; Mechanical Vibration-Measurement and Evaluation of Human Exposure to Hand-Transmitted Vibration-Part 1: General Requirements. AFNOR: Paris, France, 2002.
- Aldien, Y.; Marcotte, P.; Rakheja, S.; Boileau, P.E. Influence of Hand-Arm Posture on Biodynamic Response of the Human Hand-Arm Exposed to Zh-Axis Vibration. Int. J. Ind. Ergon. 2006, 36, 45–59. [Google Scholar] [CrossRef]
- Bouillard, K.; Nordez, A.; Hug, F. Estimation of Individual Muscle Force Using Elastography. PLoS ONE 2011, 6, e0029261. [Google Scholar] [CrossRef] [PubMed]
- Noël, C.; Settembre, N.; Reda, M.; Jacquet, E. A Multiscale Approach for Predicting Certain Effects of Hand-Transmitted Vibration on Finger Arteries. Vibration 2022, 5, 213–237. [Google Scholar] [CrossRef]
- ISO 10068:2012; Mechanical Vibration and Shock-Mechanical Impedance of the Human Hand-Arm System at the Driving Point. ISO: Geneva, Switzerland, 2012.
- Rouze, N.C.; Wang, M.H.; Palmeri, M.L.; Nightingale, K.R. Finite Element Modeling of Impulsive Excitation and Shear Wave Propagation in an Incompressible, Transversely Isotropic Medium. J. Biomech. 2013, 46, 2761–2768. [Google Scholar] [CrossRef] [PubMed]
| Isotropic Muscle | Anisotropic Muscle with Maximum Activation | |||
|---|---|---|---|---|
| No Activation | Maximum Activation | Longitudinal | Transversal | |
| Shear elastic modulus | Not used | Not used | µL = 121.0 kPa | µT = 9.0 kPa |
| Young’s modulus | EL = 22.4 kPa | EL = 338.8 kPa | EL = 338.8 kPa | ET = 25.2 kPa |
| Poisson’s ratio | υL = 0.499 | υL = 0.499 | υL = 0.499 | υT = 0.963 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vauthier, S.; Noël, C.; Settembre, N.; Ngo, H.H.P.; Gennisson, J.-L.; Chambert, J.; Foltête, E.; Jacquet, E. Factoring Muscle Activation and Anisotropy in Modelling Hand-Transmitted Vibrations: A Preliminary Study. Proceedings 2023, 86, 12. https://doi.org/10.3390/proceedings2023086012
Vauthier S, Noël C, Settembre N, Ngo HHP, Gennisson J-L, Chambert J, Foltête E, Jacquet E. Factoring Muscle Activation and Anisotropy in Modelling Hand-Transmitted Vibrations: A Preliminary Study. Proceedings. 2023; 86(1):12. https://doi.org/10.3390/proceedings2023086012
Chicago/Turabian StyleVauthier, Simon, Christophe Noël, Nicla Settembre, Ha Hien Phuong Ngo, Jean-Luc Gennisson, Jérôme Chambert, Emmanuel Foltête, and Emmanuelle Jacquet. 2023. "Factoring Muscle Activation and Anisotropy in Modelling Hand-Transmitted Vibrations: A Preliminary Study" Proceedings 86, no. 1: 12. https://doi.org/10.3390/proceedings2023086012
APA StyleVauthier, S., Noël, C., Settembre, N., Ngo, H. H. P., Gennisson, J.-L., Chambert, J., Foltête, E., & Jacquet, E. (2023). Factoring Muscle Activation and Anisotropy in Modelling Hand-Transmitted Vibrations: A Preliminary Study. Proceedings, 86(1), 12. https://doi.org/10.3390/proceedings2023086012






