3. Results and Discussion
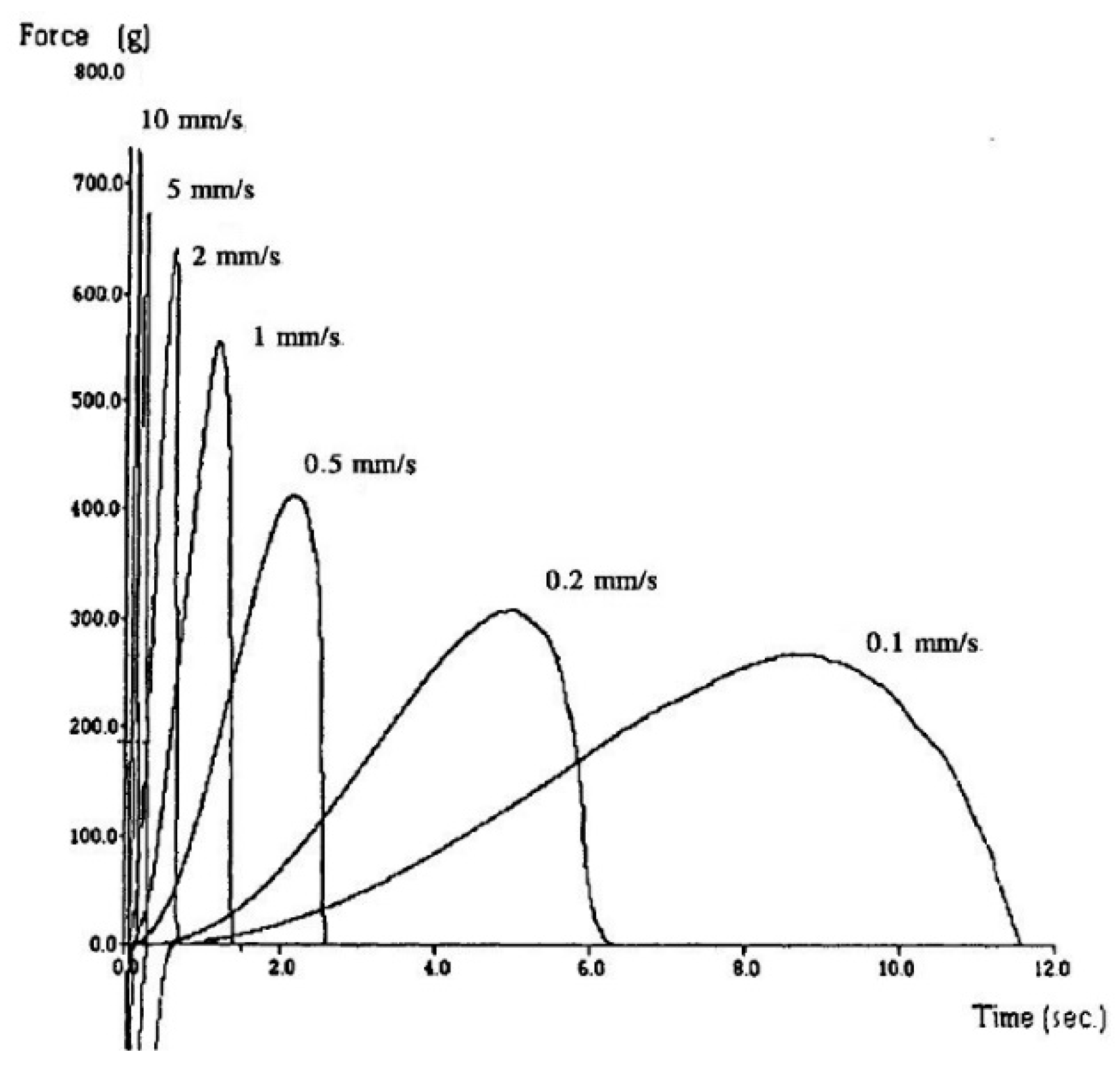
The spread of the peaks in
Figure 1 was resolved by transposing the horizontal time axis to distance.
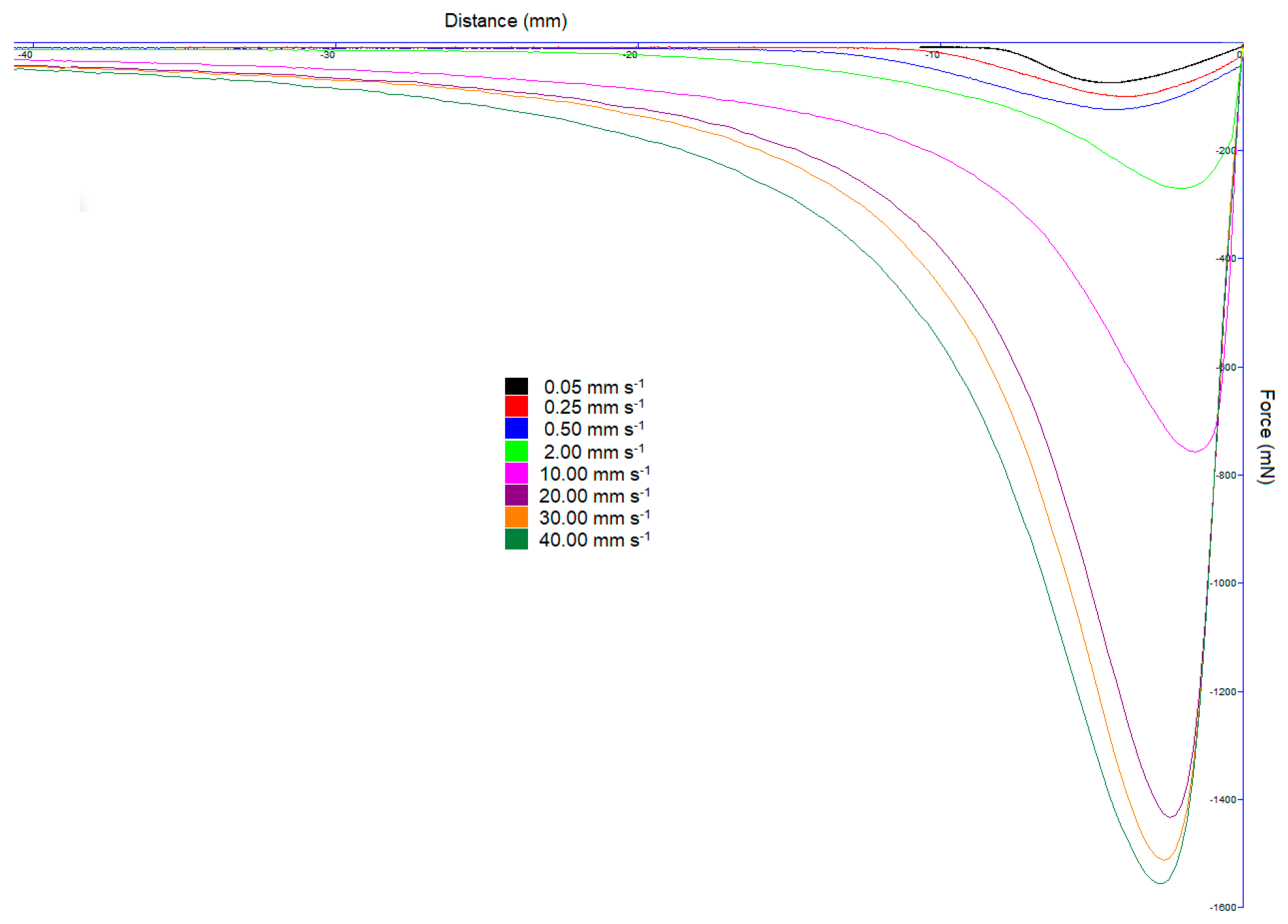
Figure 2 has the same experimental design as undertaken by Hoseney and Smewing [
4], with a range of separation speeds, which almost span the capability of the texture analyser used. In
Figure 2, we have drawn the curves as negative peaks; however, throughout this discussion, we will refer to the peak as the maximum force (as referring to a minimum force makes little sense).
By plotting the distance of separation as opposed to time on the horizontal axis, we observe that the distance to the negative peak is roughly the same regardless of the speed of the probe. This is consistent with Hoseney and Smewing [
4], though not at all obvious from
Figure 1. In contrast, the distance that the probe moves from the liquids’ plane surface to the maximum negative peak is both visibly similar and intuitively the same for all probe speeds in
Figure 2. In
Figure 1, the areas under the curves are greater for the slower speeds, with the units of this quantity being force–time. In
Figure 2, the units are force–distance, and the areas under the curves are greatest for the higher speeds. Moreover, if researchers assign stickiness to the area under the curve, then the derived units of force–distance are energy or work (J).
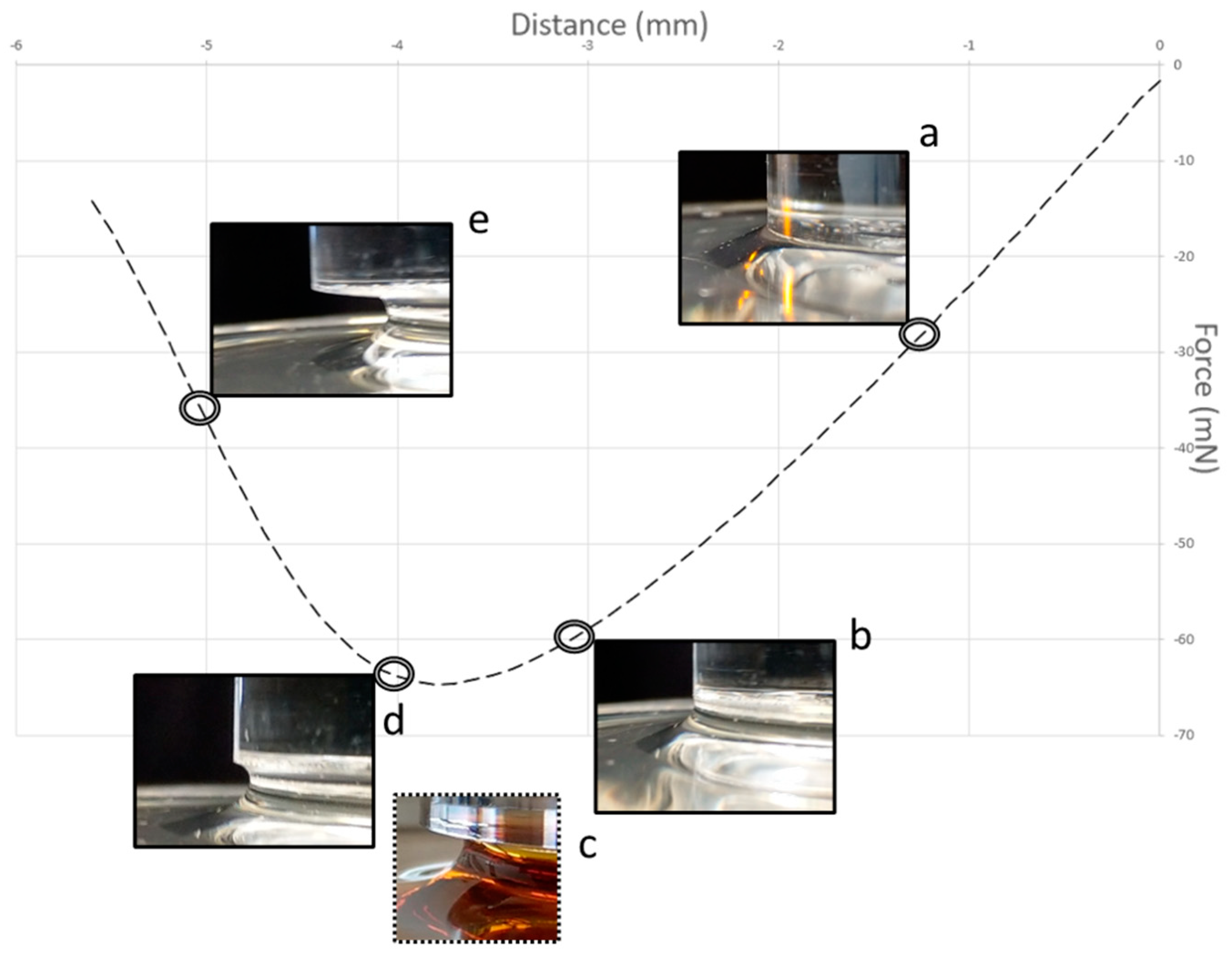
Figure 3 shows a typical curve for the separation of a probe from the surface of a sticky liquid (at a relatively low speed). When the separation is about 1.5 mm, the liquid is still in good contact with the edge of the probe, though the surface develops a curvature (inset of
Figure 3a). Before the peak is reached, the force starts to lessen (inset of
Figure 3b) as the curve starts to flatten; this is followed by the narrowing of the column of the liquid joining the probe to the body of liquid below. The curvature of the glucose syrup as the probe pulls away exhibits a concave necking (inset of
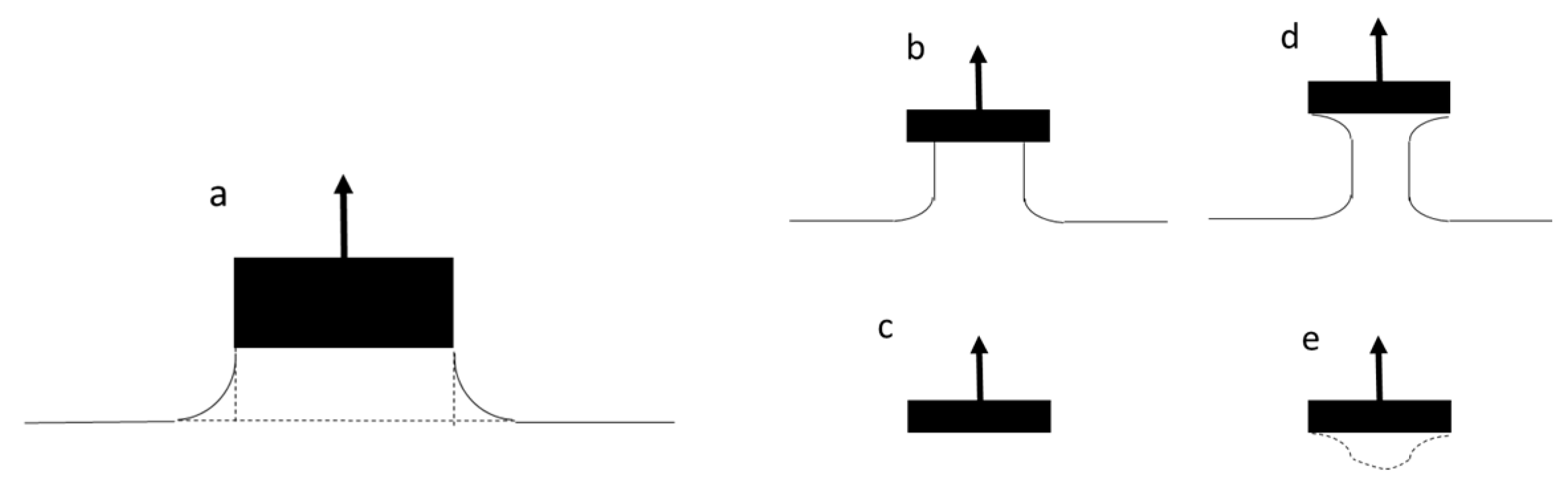
Figure 3d), holding firmly to the probe perimeter and narrowing within the liquid itself (this is shown diagrammatically in
Figure 4d). In contrast, the inset image with a broken line (inset of
Figure 3c) is for golden syrup at the peak, and while the column of the liquid thins, it does not hold fast to the perimeter of the probe but forms a narrowing cylinder attached to the base of the probe (this is shown diagrammatically in
Figure 4b). After the peak is passed, the force continues to reduce as the thickness of the column of the liquid progressively thins (e.g., inset
Figure 3e).
Stickiness has been attributed to the interaction of liquid viscosity and the interfacial properties between the probe material and the liquid [
2].
Figure 3 shows a linear region at the start of probe withdrawal, during which time the perimeter is fully in contact with the liquid. The inset images in
Figure 3 show the curvature of the liquid observed during these early stages of probe withdrawal. The forces acting downward on the probe are due to the surface tension but also the mass of the liquid below the probe and within the truncated annular region beyond the cylindrical perimeter of the probe (
Figure 4a). During the linear part of the force–distance curve, during the stages of probe withdrawal from the surface, the curvature of the liquid adhering to the perimeter of the probe is a complex relationship, which changes as the probe progressively moves up [
5].
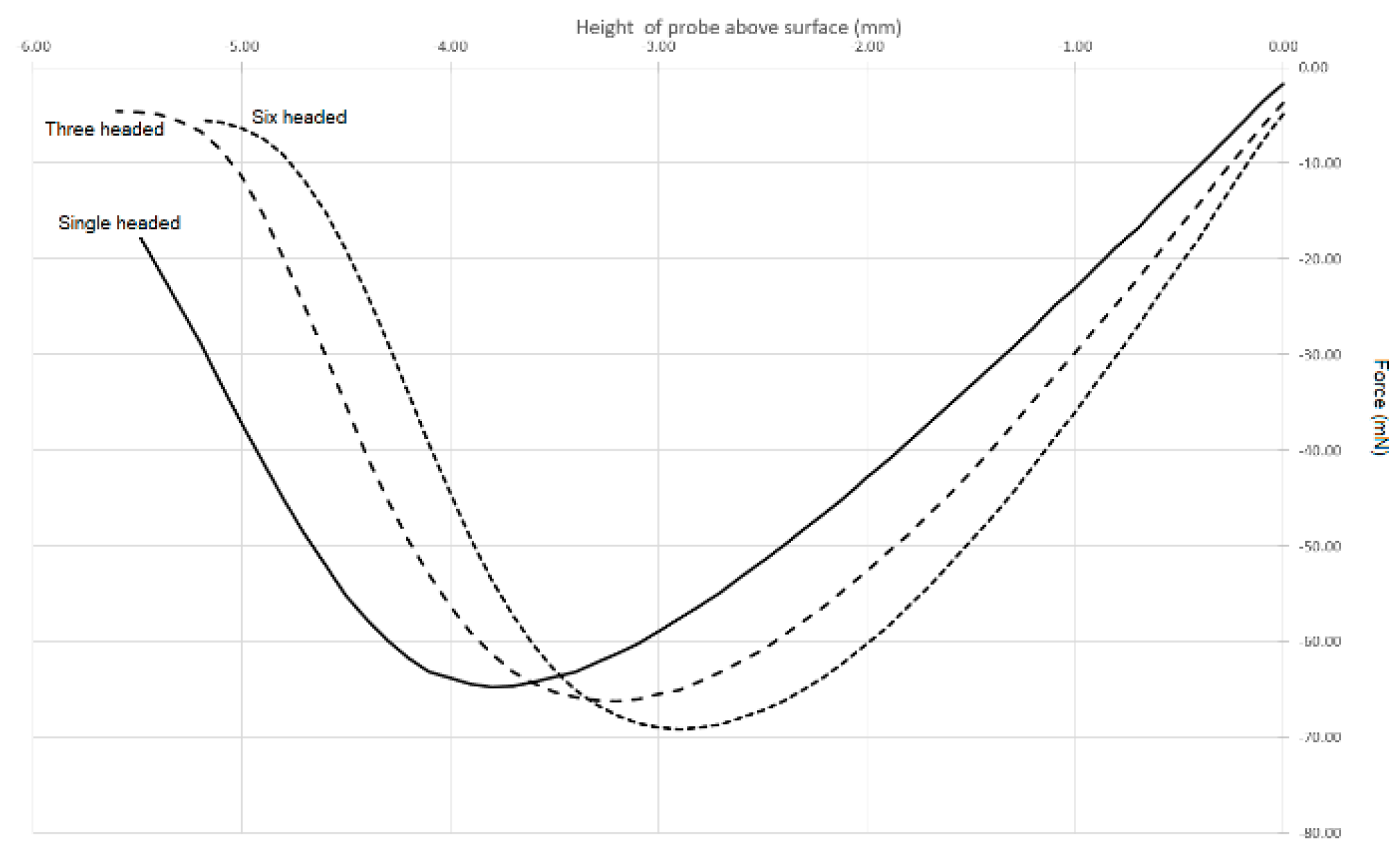
In an attempt to compensate for the effects of curvature, we developed a practical (nontheoretical) solution that utilises multiheaded probes with a common surface area in contact with the liquid. The dimensions of these probes are shown in
Table 1. Despite having the same contact area in touch with the liquid, if we sequentially undertake the stickiness test outlined above with each of these probes, we produce three different curves that do not superimpose on each other (
Figure 5). While the curves in
Figure 5 are all of a similar basic shape, the curve features, such as distance to reach the maximum negative peak, force at the maximum negative peak, area under the curve and gradient of the linear portion of the curve, are all slightly different. However, if we plot these features against the total probe perimeter, we unsurprisingly obtain good straight lines.
Furthermore, if we extrapolate such lines to zero, we effectively obtain the force we would obtain from a zero-perimeter probe. Of course, such a probe does not exist, yet the force exerted on such a virtual probe would be solely due to the mass of the liquid in a cylinder below a 962 mm2 probe.
Our zero-perimeter virtual probe overcomes problems with the unpredictable meniscus; however, we can see from
Figure 3 that, strictly speaking, the known contact area (962 mm
2) is only valid during the linear part of the curve, and this in reality excludes the use of parameters such as the peak force or the area under the curve. However, we continued to make use of the parameters of peak force and the area under the curve as measures of stickiness, albeit with our zero-perimeter curve. At least the zero-perimeter probe excludes the effect of the curved meniscus and as such better defines the system.
If the purpose of a stickiness test is to determine a defined material property, then the dimensions of the geometry are important. That is to say, in an ideal world we would be able to express the stickiness per m
2. Yet, once the curve begins to deviate from a linear force–distance behaviour, the sample geometry has changed. Ideally, we should obtain our measure of stickiness from the linear portion of the curve, otherwise we are measuring a property of ill-defined dimensions. Certainly, during the linear part of the force–distance curve, there is neither separation of the liquid from the perimeter nor necking of the sample, thus the instrumental readings obtained will relate to the contact area of the probe. Moreover, if we consider that property our zero-perimeter virtual probe, we can overcome changes in the meniscus. On this basis, using a property of this linear region such as its gradient would perhaps give us a better measure of stickiness and one that can be related to the probe geometry. Appropriately, the units of this gradient are force per unit distance (Nm
−1); in other words, a tension, which is possibly a better match for stickiness than either the peak force or work used to separate the probe. At low test speeds, the gradient of the linear portion of the force–distance curve is straightforward to measure; however, as is apparent from
Figure 2, at higher speeds, and especially with the more viscous liquids, the curve is almost vertical. It is as if the liquid cannot flow or yield, with the stress exerted by the texture analyser being unable to be dissipated, thereby rapidly rising. Although in
Figure 2 these high-speed curves appear to superimpose upon each other, if the horizontal axis is enlarged, we can discriminate between them.
Figure 1 and
Figure 2 emphasise the importance of probe withdrawal speed on the curve obtained. Making use of our multiheaded probes, we were able to estimate the various parts of the curves of our zero-perimeter virtual probe, being withdrawn from different sticky liquids at a range of speeds. Reminding ourselves that the purpose of these tests is to measure stickiness as a characteristic property of the material, we attempted to examine the relationship between the initial gradient, the maximum negative peak force and the area under the curve of the zero-perimeter virtual probe as functions of withdrawal speed.
To cope with the wide range of withdrawal speeds employed to collect the data in
Figure 6, we plotted the withdrawal speed on a log axis.
Figure 6b,c appears to show a discontinuity, remaining relatively low at slow speeds and then increasing logarithmically after some critical value, which is specific for each liquid.
Kilcast and Roberts [
6] introduced the idea of adhesive and cohesive failure based on whether a sticky liquid leaves a residue on the probe or separates cleanly when a probe is pulled out of a sticky material. We concur with Noren, Scanlon and Arntfield [
7], who observed that the cohesive/adhesive failure behaviour actually depends on the speed at which the test is undertaken. We speculate that as the probe is withdrawn from the liquid surface, at low speeds, the liquid is able to flow back to the liquid bulk, allowing it to cleanly separate from the surface of the probe, progressing from
Figure 4a,b and finishing at
Figure 4c—i.e., adhesive failure. In contrast, once we exceed the critical speed that marks the discontinuity in
Figure 6b,c, the separating probe moves faster than allows the liquid to flow back to the bulk with the result that the probe liquid behaviour progresses from
Figure 4a,d ending with
Figure 4e—i.e., cohesive failure.
Earlier, we commented on the almost vertical force–distance curves of the high-speed tests, and the idea that the material cannot dissipate the stress through flow or relaxation is consistent with stresses building within the material until that material cannot support further stretching and undergoes catastrophic failure. If the separation of the probe from the surface of the liquid is faster than allows the liquid to flow, we get cohesive failure. In this study, we are dealing with viscous syrups. Many foods are glassy materials, which are often considered to be supercooled liquids. Such materials have immensely high viscosities, which would be difficult to flow in the time frame of the test protocol outlined here. Thus, we would expect glassy materials to undergo cohesive failure. Some other foods are viscoelastic (e.g., doughs), and in such situations, we expect the failure to depend on the predominance of viscous and elastic elements present. In the case of viscoelastic materials, both the ease of flow and the elastic limits of the material will dictate whether the texture analyser imposed force can be adequately dissipated in the time frame of the test or whether we will end with cohesive failure.
In our daily life, we experience the phenomenon of stickiness in the liquids we interact with, and perhaps the approach we should take from a physical testing point of view is to employ separation speeds akin to those employed in the manual manipulation of materials with our fingers and jaw motion. Shama and Sherman [
8] used a similar approach in recommending shear rates with which to evaluate the viscosity of liquids if they are to match our human experience.