Numerical Evaluation of Protein Global Vibrations at Terahertz Frequencies by Means of Elastic Lattice Models †
Abstract
:1. Introduction
2. Materials and Methods
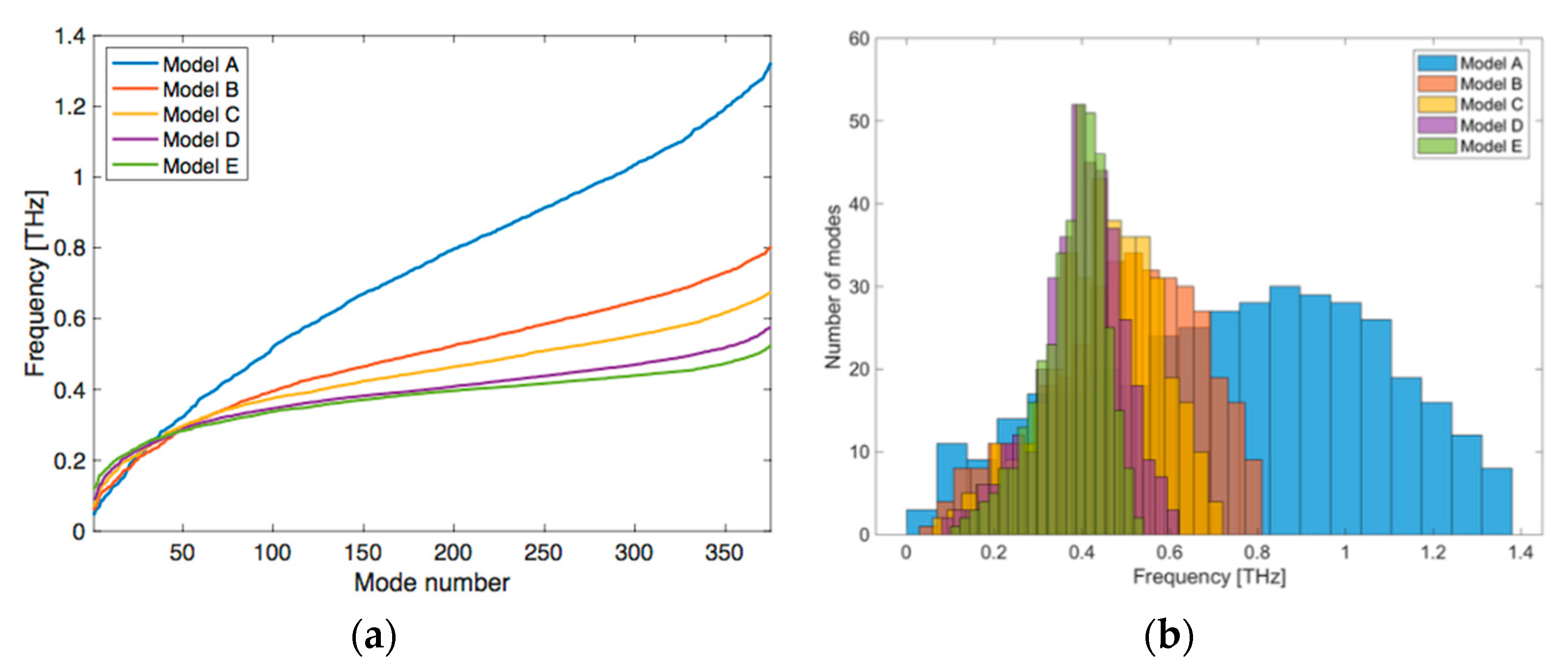
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bahar, I.; Jernigan, R.L.; Dill, K.A. Protein Actions: Principles & Modeling; Garland Science: New York, NY, USA, 2017. [Google Scholar]
- Levinthal, C. How to Fold Graciously. In Mossbauer Spectroscopy in Biological Systems; The University of Illinois Press: Champaign, IL, USA, 1969. [Google Scholar]
- Anfinsen, C.B. Principles that govern the folding of protein chains. Science 1973, 181, 223–230. [Google Scholar] [CrossRef] [PubMed]
- Karplus, M.; McCammon, J.A.; Gelin, B.R. Dynamics of folded proteins. Nature 1977, 267, 585–590. [Google Scholar]
- Teilum, K.; Olsen, J.G.; Kragelund, B.B. Functional aspects of protein flexibility. Cell. Mol. Life Sci. 2009, 66, 2231. [Google Scholar] [CrossRef] [PubMed]
- Karplus, M.; Kuriyan, J. Molecular dynamics and protein function. Proc. Natl. Acad. Sci. USA 2005, 102, 6679–6685. [Google Scholar] [CrossRef] [PubMed]
- Levitt, M.; Sander, C.; Stern, P.S. Protein normal-mode dynamics: Trypsin inhibitor, crambin, ribonuclease and lysozyme. J. Mol. Biol. 1985, 181, 423–447. [Google Scholar] [CrossRef]
- Tirion, M.M. Large amplitude elastic motions in proteins from a single-parameter, atomic analysis. Phys. Rev. Lett. 1996, 77, 1905–1908. [Google Scholar] [CrossRef] [PubMed]
- Bahar, I.; Atilgan, A.R.; Erman, B. Direct evaluation of thermal fluctuations in proteins using a single-parameter harmonic potential. Fold. Des. 1997, 2, 173–181. [Google Scholar] [CrossRef]
- Atilgan, A.R.; Durell, S.R.; Jernigan, R.L.; Demirel, M.C.; Keskin, O.; Bahar, I. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophys. J. 2001, 80, 505–515. [Google Scholar] [CrossRef]
- Scaramozzino, D.; Lacidogna, G.; Piana, G.; Carpinteri, A. A finite-element-based coarse-grained model for global protein vibration. Meccanica 2019, 54, 1927–1940. [Google Scholar] [CrossRef]
- Available online: https://www.lusas.com (accessed on 21 December 2020).
- Carpinteri, A. Advanced Structural Mechanics; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2017. [Google Scholar]
- Eyal, E.; Lum, G.; Bahar, I. The anisotropic network model web server at 2015 (ANM 2.0). Bioinformatics 2015, 31, 1487–1489. [Google Scholar] [CrossRef] [PubMed]
- Dykeman, E.C.; Sankey, O.F. Normal mode analysis and applications in biological physics. J. Phys. Condens. Matter 2010, 22, 423202. [Google Scholar] [CrossRef] [PubMed]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef]
- Ben-Avraham, D. Vibrational normal-mode spectrum of globular proteins. Phys. Rev. B 1993, 47, 14559–14560. [Google Scholar] [CrossRef] [PubMed]
- Haliloglu, T.; Bahar, I.; Erman, B. Gaussian dynamics of folded proteins. Phys. Rev. Lett. 1997, 79, 3090–3093. [Google Scholar] [CrossRef]
| Model | Cutoff (Å) | Mean Length of the Elastic Bars (Å) | EA (pN) | Stiffness of the Mean Connection (N/m) | Correlation Bnum vs Bexp |
|---|---|---|---|---|---|
| A | 8 | 5.71 | 831 | 1.455 | 0.57 |
| B | 10 | 7.21 | 235 | 0.326 | 0.67 |
| C | 12 | 8.61 | 124 | 0.144 | 0.66 |
| D | 15 | 10.59 | 71 | 0.067 | 0.69 |
| E | 20 | 13.46 | 45 | 0.033 | 0.72 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scaramozzino, D.; Lacidogna, G.; Piana, G.; Carpinteri, A. Numerical Evaluation of Protein Global Vibrations at Terahertz Frequencies by Means of Elastic Lattice Models. Proceedings 2020, 67, 8. https://doi.org/10.3390/ASEC2020-07518
Scaramozzino D, Lacidogna G, Piana G, Carpinteri A. Numerical Evaluation of Protein Global Vibrations at Terahertz Frequencies by Means of Elastic Lattice Models. Proceedings. 2020; 67(1):8. https://doi.org/10.3390/ASEC2020-07518
Chicago/Turabian StyleScaramozzino, Domenico, Giuseppe Lacidogna, Gianfranco Piana, and Alberto Carpinteri. 2020. "Numerical Evaluation of Protein Global Vibrations at Terahertz Frequencies by Means of Elastic Lattice Models" Proceedings 67, no. 1: 8. https://doi.org/10.3390/ASEC2020-07518
APA StyleScaramozzino, D., Lacidogna, G., Piana, G., & Carpinteri, A. (2020). Numerical Evaluation of Protein Global Vibrations at Terahertz Frequencies by Means of Elastic Lattice Models. Proceedings, 67(1), 8. https://doi.org/10.3390/ASEC2020-07518







