Spatiotemporal Graph Imaging Associated with Multilevel Atomic Excitations ^†

Abstract

In this paper, we establish a graph imaging technique to manifest local stabilization within atomic systems of multiple levels. Specifically, we address the interrelation between local stabilization and image entropy. As an example, we consider the mutual interaction of two pair of pulses propagating in a double-$\Lambda$ configuration. Thus, we have two different sets of two pulses that share the same shape and phase, initially. The first (second) set belongs to lower (upper) -$\Lambda$ subsystems, respectively. The configuration of two pair of pulses is considered as a dynamical graph model with four nodes. The dynamic transition matrix describes the connectivity matrix in the static graph model. It is to be emphasized that the graph and its image have the same transition matrix. In particular, the graph model exposes the stabilization in terms of the singular-value decomposition of energies for the transition matrix, that is, irrespectively of the structure of the transition matrix. The image model of the graph displays the details of the matrix structure in terms of row and column probabilities. Therefore, it enables one to study conditional probabilities and mutual information inherent in the network of the graph. Furthermore, the graph imaging provides the main row/column contribution to the transition matrix in terms of image entropy. Our results show that image entropy exposes spatial dependence, which is irrelevant to graph entropy.

1. Introduction

Quantum graphs are often implemented to model and simulate quantum systems in nuclear, molecular, and atomic physics [1,2,3,4]. The graph structure is basically composed of nodes (vertices) and links (edges), as well as a connectivity matrix that describes the strength of links between nodes. The nature of vertices and edges of the graph is strongly dependent on the system considered [2,3,4,5]. A molecular quantum graph consists of a large number of vertices. As an example, Rawlinson considered 120 nodes for the quantum graph to describe the ro-vibrational states of protonated methane molecular ion [2]. In such a quantum graph, the vertices correspond to energy minima on the potential energy surface of the compound system, and the links represent low-energy paths between vertices. In computational neuroscience contexts, has been demonstrated how the brain network can be represented by a graph [5]. The nodes in the brain graph correspond to a set of brain regions that perform specific tasks, and the edges correspond to functional connections. The connectivity matrix describes connections of different regions of the human brain in the brain-graph model. Graphs are classified into static and dynamic graphs. Dynamic graphs attribute their time dependence to the inclusion of nodes [6] or the fluctuation of the links in time. Wong considered dynamic graphs as continuous-time quantum walks [7]. There is progress in the subject of graphs and image processing in different fields. In this short communication, we briefly mention some of these efforts. Recently, Drinko et al. reported that quantum graphs could be used to construct quantum devices [8]. Furthermore, a variety of signal processing techniques for graphs and networks has been discussed in [9]. Finally, image processing has become a powerful diagnostic tool in medicine and biology [10].

Recently, we introduced a dynamical graph model (DGM) to simulate the propagation of short pulses in multilevel atomic media [4]. In that model graph, nodes are represented by atomic states of hyperfine structure (hf) associated with the $D_1$ line in ${}^{87}Rb$ vapor. The transition matrix is comprised of the density matrix components (DMCs) of different ranks that are accessible to the atomic system. Furthermore, the transition matrix is described by Maxwell fields coupling the hf states. The spatiotemporal behavior is given in terms of the Bloch equations for the density matrix and the reduced Maxwell field equations. We realized the graph with four nodes in different images, by which we mean that we made different realizations of the two-dimensional transition matrix connecting the nodes of the graph [11].

Throughout our analysis of the graph model for the atomic structure, we mainly characterized the graph model using mutual information (MI) inherent in the graph network [12] and references therein. We compared the spatial dependence of mutual information against the results of spatial scattering of light from pulses in the course of their propagation to have a realistic graph model describing the atomic structure. Thus, we may able to interpret the mutual information correlations. Therefore, the statistical significance of mutual information in light scattering was tested. Recently, the statistical significance of mutual information between a galaxy and its large environment was reported [13]. In the present communication, we are interested in the total light scattered by pulses. Therefore, we do not intend to deal with the angular distribution of the mutual information.

This paper displays the structure of the transition matrix in terms of transient Bloch metrics. This is a simple description that can be generally realized without invoking the irreducible tensorial set of the density matrix (ITSDM) [14]. The ITSDM reflects all the accessible information to the atomic system. We have provided two irreducible bases for describing the atomic structure under a hyperfine structure [15,16]. The elements of the connectivity matrix are enrichment through different multipole connections of coherence as well as looping and self-looping of the nodes. Ignoring the ITSDM, the dimensions of the product space are highly reduced. However, we cannot write the DMCs of the third and fourth ranks due to the lack of implicit rank dependence. This paper introduces new dependence of the transition matrix on the Bloch metrics with six links. In such a simple structure that ignores the ITSDM, there are ten DMCs, corresponding to six links and four populations as loops. Alternatively, in this paper, the links are governed by the space–time evolution of the Maxwell–Bloch equations (MBEs) with 28 components.

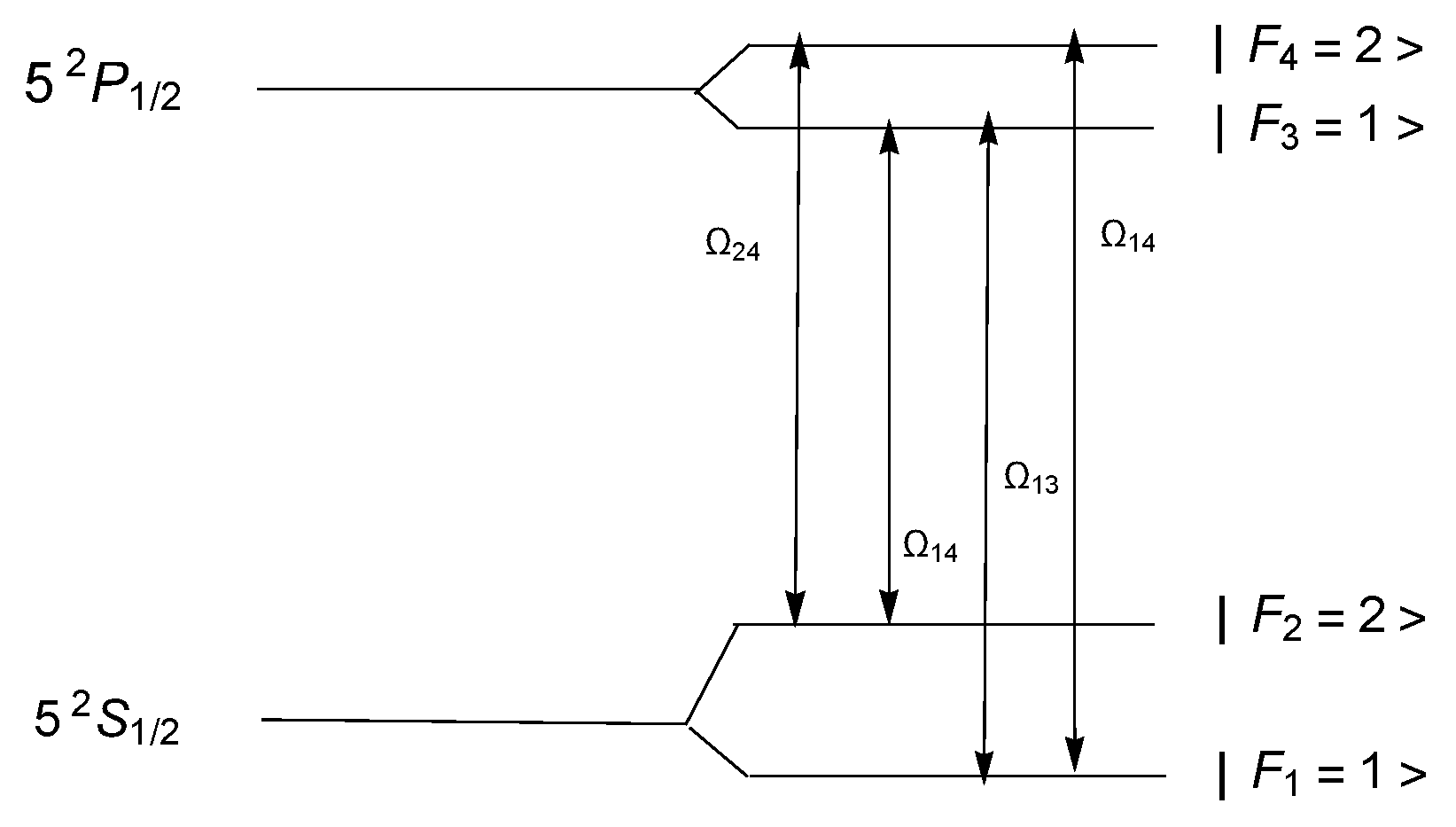
2. The Atomic System

The atomic scheme addressed in this paper is depicted in Figure 1. It shows hyperfine states and the Rabi frequencies as ${\Omega }_{ij}$, where $i=3,4$ and $j=1,2$. The state of the dressed atom is described by the Liouville–von Neumann type equation [15]. We shall make use of relative units. The relative retarded time in a frame moving with the pulse is $\tau =\gamma (t-z/c)$.

The dimensionless spatial variable is given as $\zeta ={\alpha }^{{}^{\prime }}(z+ct)$, where t is the time, c is the velocity of light, z is the spatial variable, and ${\alpha }^{{}^{\prime }}$ is the absorption coefficient of one of the pulses at the injection point. The atom–field coupling v is defined as $v=\frac{d_{r}E}{2\sqrt{3}\hslash }$, where $d_r$ is the reduced dipole moment of the optical transition and E is the electric field amplitude. The Rabi frequency is related to atom–field coupling by the relation: $\Omega =\sqrt{8}v$. The relative atom–field coupling becomes $\mathrm{v}=v/\gamma$, and $\gamma$ is the spontaneous decay rate of the atomic excited state $P_{1/2}$. We have 28 density matrix components (DMCs), ${\rho }_{\alpha \beta }^{\left(Fm\right)}$, associated with the $D_1$ line, taking into account the hf structure. The labels $\alpha$ and $\beta$ take values from 1 to 4. The labels F and m denote the tensor rank and the magnetic quantum number, respectively. The DMCs of the atomic polarizations are represented by ${\rho }_{13}^{\left(1m\right)}$, ${\rho }_{14}^{\left(1m\right)}$, ${\rho }_{23}^{\left(1m\right)}$, and ${\rho }_{24}^{\left(1m\right)}$. The magnetic quantum number $m=0$, as we consider linear polarization. We are interested in the resonant pulse propagation. We shall assume a $t^2$-Gaussian shape for the injected pulse’s envelope in the form $v\left(t\right)=64\sqrt{2}\pi v_0/27{(t/T_p)}^2\exp [-8/9\pi {(t/T_p)}^2]$, where $v_0$ is the mean amplitude of the pulse and $T_p$ is its time duration. The reduced Maxwell-field equations in a frame moving with the pulse can be written as

$$\begin{array}{c}\partial {\mathrm{v}}_{13}(\zeta ,\tau )/\partial \zeta =-{\rho }_{13}^{\left(10\right)}(\zeta ,\tau ),\partial {\mathrm{v}}_{14}(\zeta ,\tau )/\partial \zeta ={\rho }_{14}^{\left(10\right)}(\zeta ,\tau ),\hfill \\ \partial {\mathrm{v}}_{23}(\zeta ,\tau )/\partial \zeta =-{\rho }_{23}^{\left(10\right)}(\zeta ,\tau ),\partial {\mathrm{v}}_{24}(\zeta ,\tau )/\partial \zeta ={\rho }_{24}^{\left(10\right)}(\zeta ,\tau ).\hfill \end{array}$$

(1)

In the following, we describe a graph imaging of the multilevel structure considered. For a detailed description of the irreducible tensorial sets describing the atomic system and the Maxwell–Bloch equations, please see our recent communication [17].

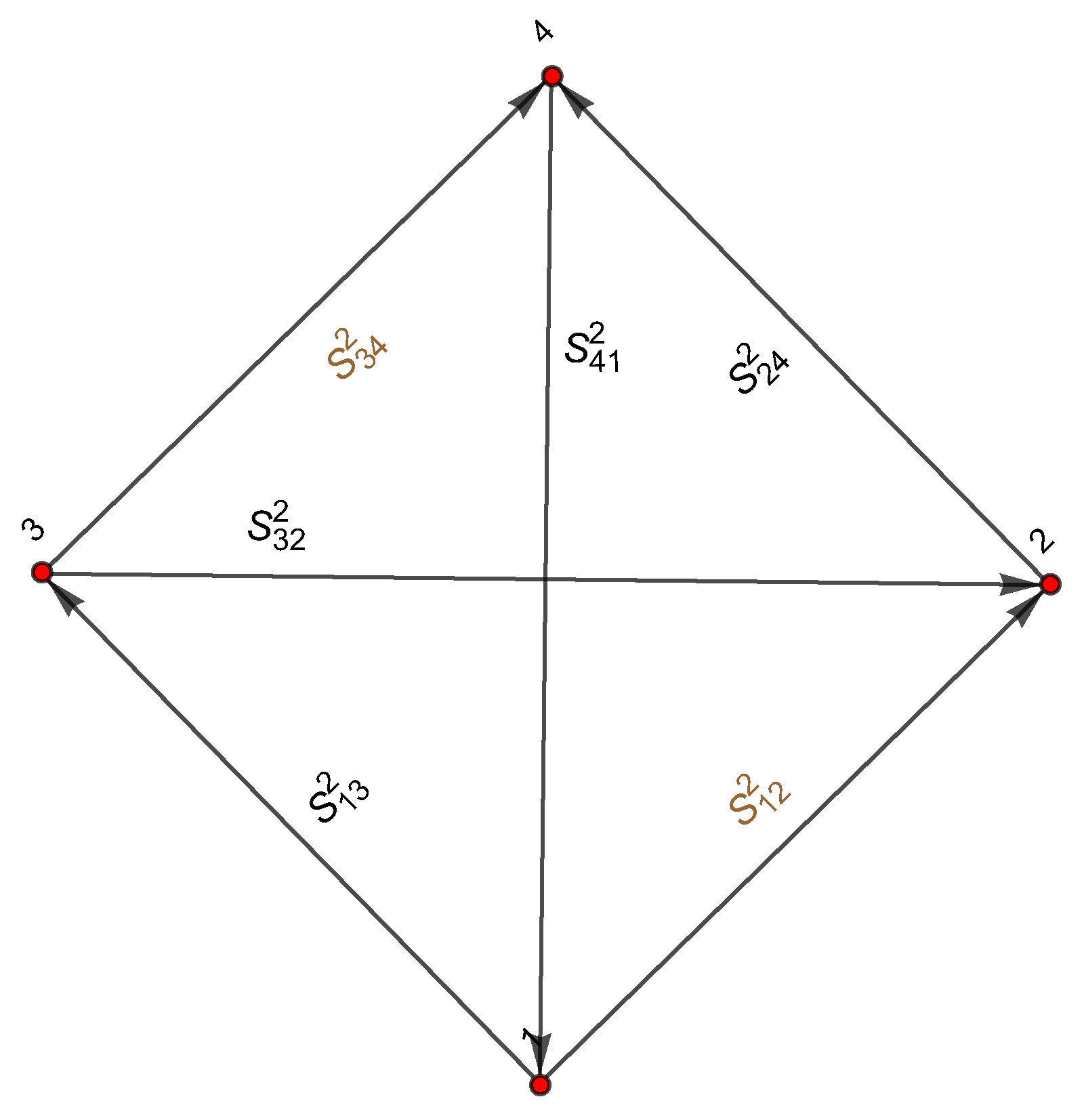
3. Graph Imaging

Recently, we have presented the transition matrix associated with the graph of the hf scheme depicted in Figure 1. The transition matrix is composed of the atomic and the field contributions. The atomic contributions are density matrix components that are maximally accessible to the $D_1$ line. The DMC is arranged into different irreducible tensorial sets that are allowed by dipole and quadrupole transitions. The field contribution to the transition matrix is mainly attributed to the dipole-allowed transitions only. According to the singular value decomposition (SVD) technique, the system can be characterized by its leading eigenvalues. Alternatively, in this communication, we shall pay attention to different types of transition matrices. The proposed transition matrix is constructed from nodes and links. The nodes represent the atomic energy state, while the links represent the Bloch metrics associated with each transition allowed by dipoles or quadrupoles. These are positive quantities, and there is no need for SVD to obtain positive values for the eigenvalues. Figure 2 presents an image structure with four nodes. The figure shows the diamond structure with a closed loop. The diagonals are connected by dipole-allowed transitions. We are interested only in the resonant interaction of the four pulses with the double-$\Lambda$ atomic medium. The steady-state analysis of laser phases in the ⋄ configuration of electromagnetically induced transparency has been addressed in [18].

The image in Figure 2 shows that there are two links that are attributed to dipole-forbidden transitions. Let us write the transition matrix as

$$M_1(t;z)=\left(\begin{array}{cccc}{S}_{13}^2(t;z)& S_{32}^2(t;z)& S_{24}^2(t;z)& S_{41}^2(t;z)\end{array}\right),$$

(2)

where $S_{ij}^2(t;z)$ represents the Bloch metric associated with the transition $|j\rangle \leftrightarrow |i\rangle$. The image $M_1(t;z)$ presents the transition matrix as being composed from dipole transitions only. The brown links in Figure 2 are omitted. However, one can draw the closed-loop diamond structure with dipole-allowed transitions presenting links. We study the transition matrix $M_1(t;z)$ at some location point in space z and at different time distributions. This reduces the dimension of the matrix $M_1(t;z)$ to be of the length of the interaction time considered. The rows of the matrix $M_1(t;z)$ cannot be exchanged due to the direction of the arrow of time. So, the influence of the permutation entropy is highly reduced. The permutations are only along the columns of the transition matrix. By constructing the Bloch metrics, one can write

$$\begin{array}{c}{S}_{13}^2(t;z)=\frac{1}{2}{({\rho }_{11}^{\left(00\right)}(t;z)-{\rho }_{33}^{\left(00\right)}(t;z))}^2+{\left({\rho }_{13}^{\left(1m\right)}(t;z)\right)}^2+{\left({\rho }_{31}^{\left(1m\right)}(t;z)\right)}^2,\hfill \\ S_{14}^2(t;z)=\frac{5}{8}{(\sqrt{3/5}{\rho }_{44}^{\left(00\right)}(t;z)-{\rho }_{11}^{\left(00\right)}(t;z))}^2+{\left({\rho }_{14}^{\left(1m\right)}(t;z)\right)}^2+{\left({\rho }_{41}^{\left(1m\right)}(t;z)\right)}^2,\hfill \\ S_{14}^2(t;z)=\frac{3}{8}{(\sqrt{5/3}{\rho }_{33}^{\left(00\right)}(t;z)-{\rho }_{22}^{\left(00\right)}(t;z))}^2+{\left({\rho }_{23}^{\left(1m\right)}(t;z)\right)}^2+{\left({\rho }_{32}^{\left(1m\right)}(t;z)\right)}^2,\hfill \\ S_{24}^2(t;z)=\frac{1}{2}{({\rho }_{44}^{\left(00\right)}(t;z)-{\rho }_{22}^{\left(00\right)}(t;z))}^2+{\left({\rho }_{24}^{\left(1m\right)}(t;z)\right)}^2+{\left({\rho }_{42}^{\left(1m\right)}(t;z)\right)}^2.\hfill \end{array}$$

(3)

The transition matrix $M_2(t;z)$ is comprised of the primed components as

$$M_2(t;z)=\left(\begin{array}{cccc}{{}^{\prime }{S}^2}_{13}(t;z)& {{}^{\prime }{S}^2}_{32}(t;z)& {{}^{\prime }{S}^2}_{24}(t;z)& {{}^{\prime }{S}^2}_{41}(t;z)\end{array}\right).$$

(4)

For such a case, the Bloch metrics become

$$\begin{array}{c}{{}^{\prime }{S}^2}_{13}(t;z)={\left({\rho }_{11}^{\left(00\right)}(t;z)\right)}^2+{\left({\rho }_{33}^{\left(00\right)}(t;z)\right)}^2+{\left({\rho }_{13}^{\left(1m\right)}(t;z)\right)}^2+{\left({\rho }_{31}^{\left(1m\right)}(t;z)\right)}^2,\hfill \\ {{}^{\prime }{S}^2}_{14}(t;z)={\left({\rho }_{44}^{\left(00\right)}(t;z)\right)}^2+{\left({\rho }_{11}^{\left(00\right)}(t;z)\right)}^2+{\left({\rho }_{14}^{\left(1m\right)}(t;z)\right)}^2+{\left({\rho }_{41}^{\left(1m\right)}(t;z)\right)}^2,\hfill \\ {{}^{\prime }{S}^2}_{23}(t;z)={\left({\rho }_{33}^{\left(00\right)}(t;z)\right)}^2+{\left({\rho }_{22}^{\left(00\right)}(t;z)\right)}^2+{\left({\rho }_{23}^{\left(1m\right)}(t;z)\right)}^2+{\left({\rho }_{32}^{\left(1m\right)}(t;z)\right)}^2,\hfill \\ {{}^{\prime }{S}^2}_{24}(t;z)={\left({\rho }_{44}^{\left(00\right)}(t;z)\right)}^2+{\left({\rho }_{22}^{\left(00\right)}(t;z)\right)}^2+{\left({\rho }_{24}^{\left(1m\right)}(t;z)\right)}^2+{\left({\rho }_{42}^{\left(1m\right)}(t;z)\right)}^2.\hfill \end{array}$$

(5)

Let us construct the third transition matrix. It accounts for the full graph, which includes Raman transitions:

$$M_3(t;z)=\left(\begin{array}{cccccc}{{}^{\prime }{S}^2}_{13}(t;z)& {{}^{\prime }{S}^2}_{32}(t;z)& {{}^{\prime }{S}^2}_{24}(t;z)& {{}^{\prime }{S}^2}_{41}(t;z)& {{}^{\prime }{S}^2}_{12}(t;z)& {{}^{\prime }{S}^2}_{34}(t;z)\end{array}\right).$$

(6)

The Bloch metrics associated with the Raman transitions become

$$\begin{array}{c}{{}^{\prime }{S}^2}_{12}(t;z)={\left({\rho }_{11}^{\left(00\right)}(t;z)\right)}^2+{\rho }_{22}^{\left(00\right)}{(t;z))}^2+{\left({\rho }_{12}^{\left(2m\right)}(t;z)\right)}^2+{\left({\rho }_{21}^{\left(2m\right)}(t;z)\right)}^2,\hfill \\ {{}^{\prime }{S}^2}_{34}(t;z)={\left({\rho }_{33}^{\left(00\right)}(t;z)\right)}^2+{\left({\rho }_{44}^{\left(00\right)}(t;z)\right)}^2+{\left({\rho }_{34}^{\left(2m\right)}(t;z)\right)}^2+{\left({\rho }_{43}^{\left(2m\right)}(t;z)\right)}^2.\hfill \end{array}$$

(7)

4. Image Entropy

In this section, we provide the mathematical formalism for image entropy. We introduced the transition matrix $M\left(t\right)$ associated with a model graph representing the hyperfine structure. In what follows, we aim to describe the procedure to obtain image entropy [19]. Let us note that our transition matrix is not symmetric. The first step is to normalize the transition matrix $M(t;z)$, such that

$$M_{\alpha \beta }(t;z)\leftarrow \frac{M_{\alpha \beta }(t;z)}{{\sum }_{\alpha \beta }{M}_{\alpha \beta }(t;z)}.$$

(8)

Hence, we can define:

A.

The probability, $p_{\alpha }(t;z)$, for the node to be connected,

B.

Shannon entropy, $S_{row}(t;z)$, for rows in the transition matrix $M(t;z)$,

C.

Conditional entropy, $S_{column|row}(t;z)$, for column nodes given row nodes,

D.

Mutual information, $I(t;z)$, gained through the network:

$$\begin{array}{c}\hfill I\left(M(t;z)\right)=\sum _{\alpha \beta }{M}_{\alpha \beta }(t;z){log}_2[M_{\alpha \beta }(t;z)/p_{\alpha }(t;z)p_{\beta }(t;z)].\end{array}$$

(9)

5. Numerical Results

In Section 4, we presented an alternative representation for the transition matrix. The present representation describes the graph of the multilevel structure in terms of nodes and bonds connecting the nodes. We facilitated different classes of images (trees) for the graph model. The bonds (links or edges) in our model represent the Bloch metric for the specific link between nodes. The Bloch metric depends on the atomic inversion and the coherence, whether optical or Raman. It is convenient to account for mutual information. Figure 3 depicts mutual information content in the course of propagation of the two pair of pulses considered. The MI exposes a finite number of peaks, which are localized spatially. Thus, the MI identifies four bands of spatial resonances in the course of propagation. The first band comprises a single line, whilst other bands have multi-peak structures. The multi-peak structure within each band signifies the mutual interaction and correlation by the resonant pulses in the course of propagation.

The multi-peak structure of the MI spatial resonance can be compared with the spatial fluorescence imaging based upon the scattered light at different location depths in the atomic medium. We analyzed the Poynting energy for light scattering associated with a dual-color excitation of the sodium atom in a multilevel atom [20]. Here, we intended to describe scattering in terms of cross-sections. The spatial and total cross-section for light scattering is given as

$$\sigma \left(z\right)=\frac{\gamma \int (n_3(t;z)+n_4(t;z))dt}{N_0},$$

(10)

where $N_0$ denotes the average number of photons incident on a unit area; the fraction of $\pi$ polarized scattered photons:

$${\sigma }_{\pi }\left(z\right)=\frac{\gamma \int (n_3(t;z)+n_4(t;z))dt}{3N_0}.$$

(11)

Figure 4 shows the spatial dependence of the relative cross-section. The spatial cross-section and mutual information expose banded multi-peak structures. The mutual information and cross-section display a broadened single line in the first band. The cross-section displays a well-resolved triplet of lines in the second band. The structure is broadened in mutual information behavior. The spatial dependence of mutual information does not show the threshold entropy tendency as being exposed by the graph entropy. In addition, it is not restricted to max-/min-entropy limitations. However, the row entropy of the transition matrix shows that it is bounded from above by Hartley entropy.

6. Discussion

We have facilitated a graph-imaging technique to simulate the spatiotemporal characteristics of the propagation of a pair of two pulses in resonant multilevel atomic media. The transition matrix is constructed from positive definite quantities, reflecting the strength of the bonds connecting the nodes. We have found that the Bloch metric for each two-level atom subsystem is a good measure for node connectivity. Therefore, three types of Bloch metric connectivity have been investigated. The first one provides a constrained Bloch metric to satisfy the explicit requirements of $2^{-1}{\partial }_{t}Tr{\rho }^2$, which is traceless in regards to the field. The second proposed Bloch metric measure is attributed to instantaneous behavior and is more or less geometrical. For both cases, we only studied the Bloch metrics due to dipole transitions. The third Bloch metric is a geometrical one and includes both dipole and quadrupole transitions. The constructed transition matrices are not symmetrical with respect to permutations of rows and columns. This enables us to reduce the permutation entropy. The results are insensitive to permutation of columns, as predicted by parallel computations, especially for the first case. Thus, these transition matrices quantify the image entropy with respect to its bond strengths between nodes.

In conclusion, we have two views for graph and image entropy. The graph entropy is basically dependent on the eigensystem of the graph corresponding to the schematic energy level diagram of the atom under consideration. However, the image entropy solely depends upon positive definite bond connections. The strength of these bonds measures the connectivity between nodes. With a matrix visualization for the image, we have construed the mutual information gained in the network. It has been shown that the mutual information exposes peaks in the course of propagation. The mutual information peaks show a structure that is irrelevant to the graph entropy. The information entropy quantifies the spatial resonance as compared with the spatial light scattering. We hope that our technique finds its application in light storage experiments through image segmentation and information transfer.