Co-Design and Control of a Magnetic Microactuator for Freely Moving Platforms †
Abstract
:1. Introduction
2. Methods
2.1. Modelling
2.2. Trajectory Planning and Control
2.2.1. Electromagnetic Actuation
2.2.2. Piezoelectric Actuation
2.3. Co-Design
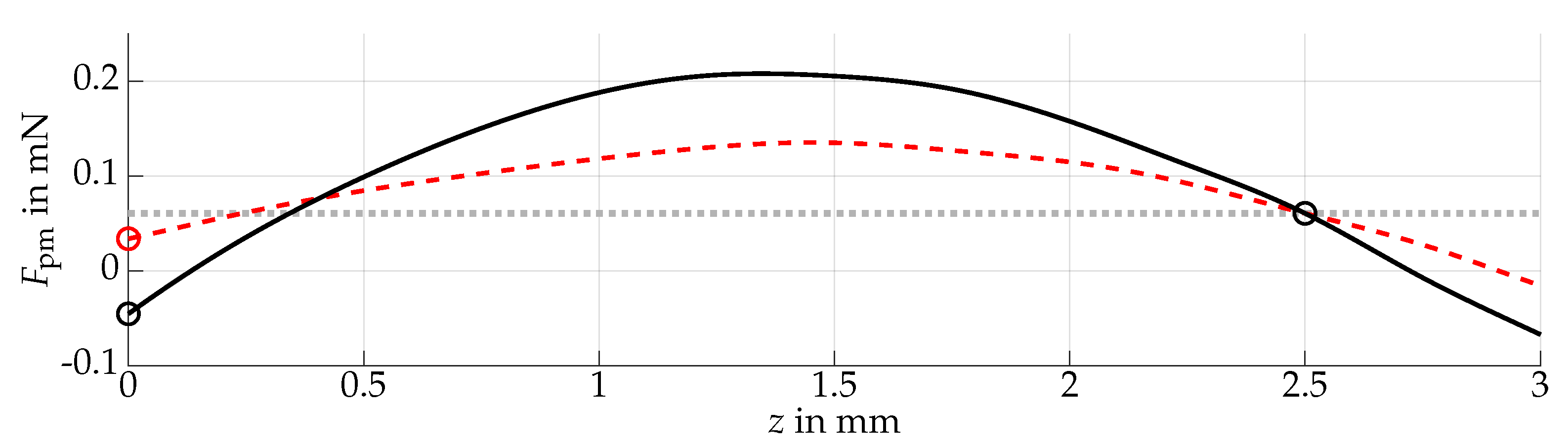
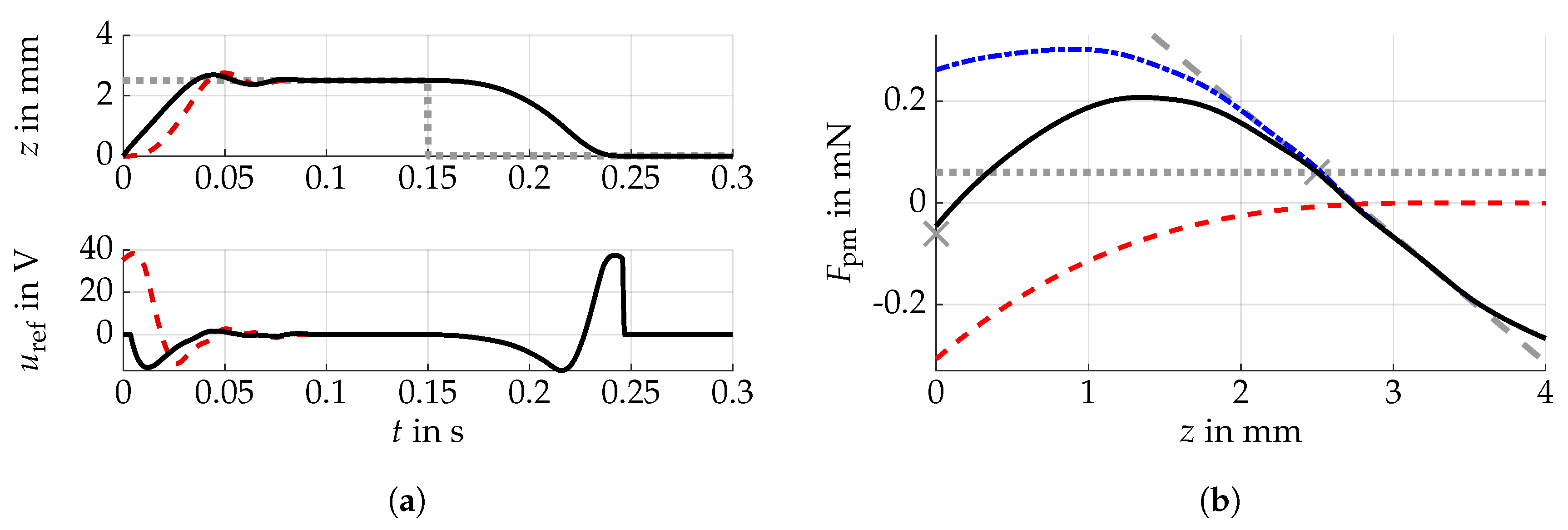
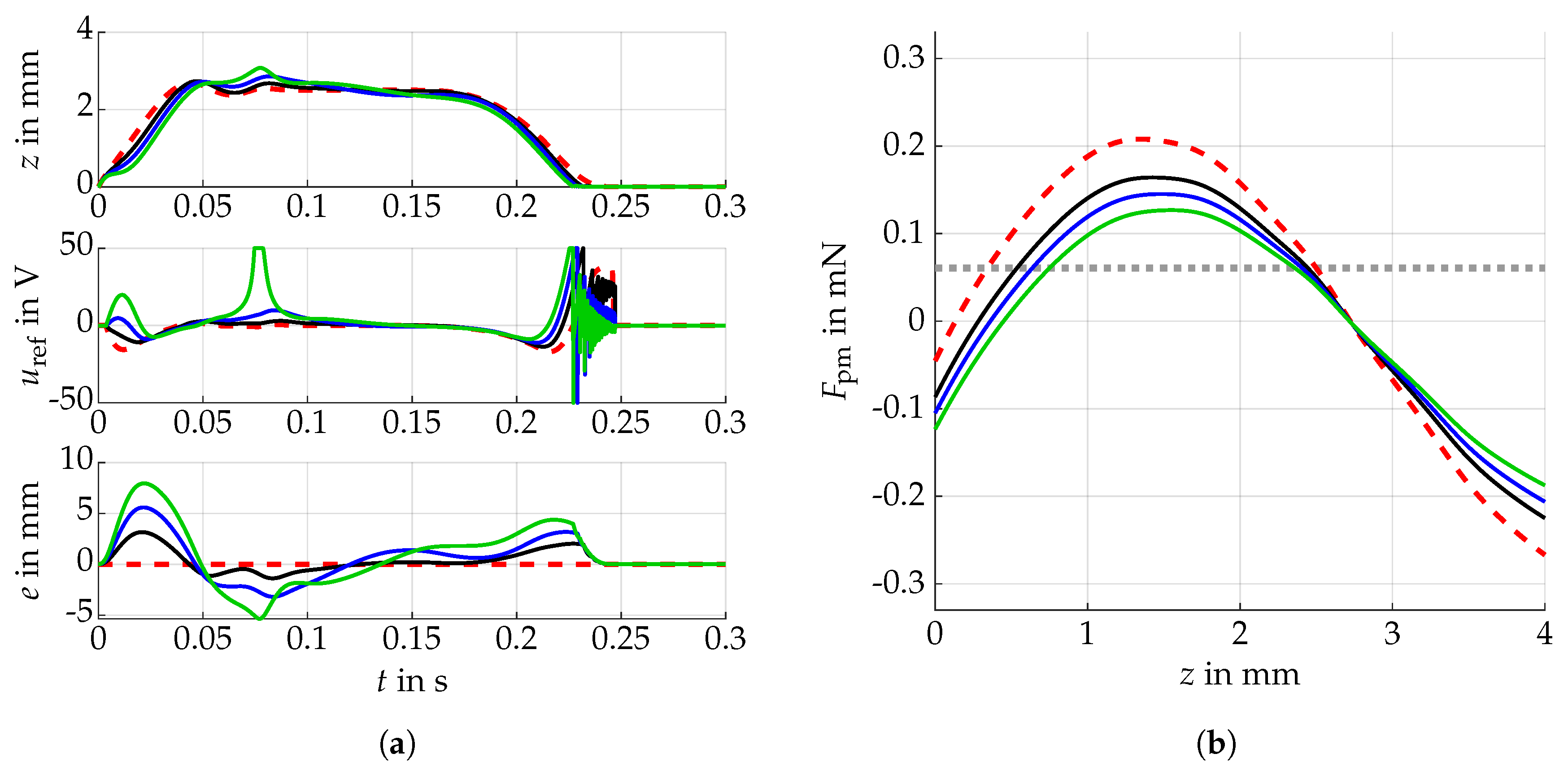
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Breguet, J.M.; Pérez, R.; Bergander, A.; Schmitt, C.; Clavel, R.; Bleuler, H. Piezoactuators for Motion Control from Centimeter to Nanometer. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Takamatsu, Japan, 31 October–5 November 2000; pp. 492–497. [Google Scholar]
- Mita, M.; Arai, M.; Tensaka, S.; Kobayashi, D. Fujita, H. A Micromachined Impact Microactuator Driven by Electrostatic Force. J. Microelectromech. Syst. 2003, 12, 37–41. [Google Scholar] [CrossRef]
- Edeler, C.; Meyer, I.; Fatikow, S. Modeling of stick-slip micro-drives. J. Micro-Nano Mechatron. 2011, 6, 65–87. [Google Scholar] [CrossRef]
- Ruffert, C.; Li, J.; Denkena, B.; Gatzen, H.H. Development and Evaluation of an Active Magnetic Guide for Microsystems With an Integrated Air Gap Measurement System. IEEE Trans. Magnet. 2007, 43, 2716–2718. [Google Scholar] [CrossRef]
- Ruffert, C.; Gehrking, R.; Ponick, B.; Gatzen, H.H. Magnetic Levitation Assisted Guide for a Linear Micro-Actuator. IEEE Trans. Magnet. 2006, 42, 3785–3787. [Google Scholar] [CrossRef]
- Poletkin, K.; Lu, Z.; Wallrabe, U.; Korvink, J.G.; Badilita, V. Stable dynamics of micro-machined inductive contactless suspensions. Int. J. Mech. Sci. 2017, 131, 753–766. [Google Scholar] [CrossRef]
- Safaeian, R.; Heydari, H. Optimal design of passive permanent magnet bearings. In Proceedings of the 27th Iranian Conference on Electrical Engineering, Yazd, Iran, 30 April–2 May 2019; pp. 458–463. [Google Scholar]
- Tzes, A.; Nikolakopoulos, G.; Dritsas, L.; Koveos, Y. Multi-Parametric Hinf Control of a Micro-actuator. In Proceedings of the 16th Triennial World Congress, Prague, Czech Republic, 4–8 July 2005; pp. 964–969. [Google Scholar]
- Zhu, G.; Lévine, J.; Praly, L.; Peter, Y. Flatness-Based Control of Electrostatically Actuated MEMS With Application to Adaptive Optics: A Simulation Study. J. Microelectromech. Syst. 2006, 15, 1165–1174. [Google Scholar] [CrossRef]
- Owusu, K.O.; Lewis, F.L. Solving the “Pull-in” Instability Problem of Electrostatic Microactuators using Nonlinear Control Techniques. In Proceedings of the 2nd IEEE International Conference on Nano/Micro Engineered and Molecular Systems, Bangkok, Thailand, 16–19 January 2007; pp. 1190–1195. [Google Scholar]
- Zhu, G.; Saydy, L. Robust Output Feedback Control of an Electrostatic Micro-Actuator. In Proceedings of the American Control Conference, New York, NY, USA, 9–13 July 2007; pp. 3192–3197. [Google Scholar]
- Peters, D.L.; Kurabayashi, K.; Papalambros, P.Y.; Ulsoy, A.G. Co-Design of a MEMS Actuator and Its Controller Using Frequency Constraints. In Proceedings of the ASME Dynamic Systems and Control Conference, Ann Arbor, MI, USA, 20–22 October 2008; pp. 801–807. [Google Scholar]
- Schütz, A.; Hu, S.; Rudnyi, E.B.; Bechtold, T. Electromagnetic System-Level Model of Novel Free Flight Microactuator. In Proceedings of the 21st International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems, Cracow, Poland, 6–27 July 2020; pp. 1–6. [Google Scholar]
- Goldfarb, M.; Celanovic, N. A lumped parameter electromechanical model for describing the nonlinear behavior of piezoelectric actuators. J. Dyn. Syst. Meas. Control 1997, 119, 478–485. [Google Scholar] [CrossRef]
- Main, J.A.; Garcia, E. Piezoelectric Stack Actuators and Control System Design: Strategies and Pitfalls. J. Guid. Control Dyn. 1997, 20, 478–485. [Google Scholar] [CrossRef]
- Agashe, J.S.; Arnold, D.P. A study of scaling and geometry effects on the forces between cuboidal and cylindrical magnets using analytical force solutions. J. Phys. D Appl. Phys. 2008, 41, 1–9. [Google Scholar] [CrossRef]
- Ravaud, R.; Lemarquand, G.; Babic, S.; Lemarquand, V.; Akyel, C. Cylindrical Magnets and Coils: Fields, Forces, and Inductances. IEEE Trans. Magnet. 2010, 46, 3585–3590. [Google Scholar] [CrossRef]
- Ansys Inc. ANSYS Electronics Desktop, Release 2020 R1; Ansys Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Specker, T.; Buchholz, M.; Dietmayer, K. Dynamical Modeling of Constraints with Friction in Mechanical Systems. In Proceedings of the 8th Vienna International Conference on Mathematical Modelling, Vienna, Austria, 18–20 February 2015; pp. 514–519. [Google Scholar]
- Fliess, M.; Lévine, J.; Martin, P.; Rouchon, P. Flatness and defect of non-linear systems: Introductory theory and examples. Int. J. Control 1995, 61, 1327–1361. [Google Scholar] [CrossRef]
- Charlet, B.; Lévine, J. On dynamic feedback linearization. Syst. Control Lett. 1989, 13, 143–151. [Google Scholar] [CrossRef]
- The MathWorks Inc. MATLAB and Global Optimization Toolbox (R2019a); The MathWorks Inc.: Natick, MA, USA, 2019. [Google Scholar]

| Variable | Description | Lower Bound | Upper Bound | Optimised Value |
|---|---|---|---|---|
| Ring magnet remanence | 1 | |||
| Ring magnet remanence | 1 | |||
| Proof mass remanence | 1 | |||
| Position of ring magnet 1 | 1 | 10 | ||
| Position of ring magnet 2 | 1 | |||
| Position of solenoid | – | |||
| Piezo actuator voltage peak | 0 | |||
| Third motion derivative | – | – | – | |
| Controller switch on time | 0 | |||
| Maximum transient time |
| Description | Value | Description | Value |
|---|---|---|---|
| Inner radius (ring magnets) | (piezo) | ||
| Outer radius (ring magnets) | Stiffness (piezo) | −1 | |
| Height (ring magnets) | Surface (piezo) | 9 2 | |
| Inner radius (solenoid) | Height (piezo) | 21 | |
| Outer radius (solenoid) | Mass (piezo) | ||
| Height (solenoid) | Diameter (proof mass) | ||
| Wire diameter (solenoid) | Height (proof mass) | ||
| Specific resistance (solenoid) | Density (proof mass) | 7874 −3 | |
| Number of coils (solenoid) | 4000 | State penalty Q (LQR) | |
| (piezo) | 360 | Input penalty R (LQR) | 1 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 8 | |||
| 28 | 0 | ||
| 0.25 | |||
| 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olbrich, M.; Schütz, A.; Kanjilal, K.; Bechtold, T.; Wallrabe, U.; Ament, C. Co-Design and Control of a Magnetic Microactuator for Freely Moving Platforms. Proceedings 2020, 64, 23. https://doi.org/10.3390/IeCAT2020-08494
Olbrich M, Schütz A, Kanjilal K, Bechtold T, Wallrabe U, Ament C. Co-Design and Control of a Magnetic Microactuator for Freely Moving Platforms. Proceedings. 2020; 64(1):23. https://doi.org/10.3390/IeCAT2020-08494
Chicago/Turabian StyleOlbrich, Michael, Arwed Schütz, Koustav Kanjilal, Tamara Bechtold, Ulrike Wallrabe, and Christoph Ament. 2020. "Co-Design and Control of a Magnetic Microactuator for Freely Moving Platforms" Proceedings 64, no. 1: 23. https://doi.org/10.3390/IeCAT2020-08494
APA StyleOlbrich, M., Schütz, A., Kanjilal, K., Bechtold, T., Wallrabe, U., & Ament, C. (2020). Co-Design and Control of a Magnetic Microactuator for Freely Moving Platforms. Proceedings, 64(1), 23. https://doi.org/10.3390/IeCAT2020-08494





