Active Disturbance Rejection Control for Double-Pump Direct-Driven Hydraulics ^†

Abstract

As a result of the energy crisis and further development of the electro-hydraulic actuator, double-pump direct driven hydraulics (DDH) was brought forward, which mainly comprises a servo motor, double fixed displacement pumps, a differential cylinder, a low-pressurized tank and auxiliary valves. To address the problems caused by uncertain parameters and unknown external disturbances of DDH, this paper proposed a control method adopting active disturbance rejection control (ADRC). Firstly, a mathematical model, including a DDH unit and a micro-crane, was created and modelled in MATLAB/Simulink. Further, the model was verified by measurement. After that, the state-space equation model of the system was derived based on its mathematical model and a third-order ADRC was designed using the constructed system state-space equation. Additionally, tracking-differentiator (TD) was employed to process the input signal transiently to avoid unnecessary oscillations, and the extended state observer (ESO) was used to accurately estimate the influence of the uncertainty and compensate by nonlinear feedback control law (NFCL). Moreover, the proposed ADRC or Proportional–Integral–Differential (PID) control was combined with the mathematical model of a micro-crane. Finally, the simulations were performed under varying loads, and the system position tracking performance were analyzed and compared. The results show that the ADRC can sufficiently suppress the unknown external disturbance, has the advantages of robustness, and improves the position tracking precision.

1. Introduction

The electro-hydraulic servo system can be roughly divided into two categories: valve-controlled system and pump-controlled system. The valve-controlled system has the characteristics of a fast dynamic response and high control accuracy, but it has disadvantages, such as significant throttling loss, low system efficiency, and severe heating. Compared with the valve-controlled system, the pump-controlled system basically eliminates the throttling loss. Hence, it significantly improves system efficiency and has the characteristics of compactness and high system integration [1,2]. In recent years, machines have to be energy-efficient due to limited and high-priced energy resources together with the increasing sensitivity of environmental issues [3,4]. Hence, pump-controlled system techniques have become the centre of focus [5,6].

However, in the pump-controlled differential cylinder system, unbalanced flow is caused by the unequal effective cross-section area of the two chambers. Much research has been carried out on this, such as using a pilot-operated check valve or solenoid-operated reversing valve [7,8], developing an asymmetric flow distribution pump [9], and proposing a double-pump or multi-pump compensation circuit [10,11,12] to solve the flow imbalance problem. Among them, the double-pump direct-driven hydraulic (DDH) system can better improve the dynamic performance and stability of the system. Then, when addressing the problem of flow imbalance, the time-varying and nonlinearity of the pump-controlled system also need to be solved. Hence, many control methods were proposed, such as adaptive fuzzy control [13], control based on disturbance observer [14,15], adaptive backstepping control or iterative backstepping control [16,17,18].

As discussed above, the DDH can effectively solve the problem of flow mismatch, but control performance of the system is affected by parameter uncertainty. Therefore, this paper proposed a control method, adopting active disturbance rejection control (ADRC) for DDH. Firstly, Section 2 introduces the principle of the DDH, establishes the mathematical model of a micro-crane and derives the system state-space equation. Then, Section 3 gives the design procedure of the proposed ADRC controller based on the system state-space. Section 4 performs simulation and compares the tracking performance of the ADRC controller with the Proportional–Integral–Differential (PID) controller. Finally, Section 5 draws some conclusions.

2. Modelling

2.1. Working Principle of DDH

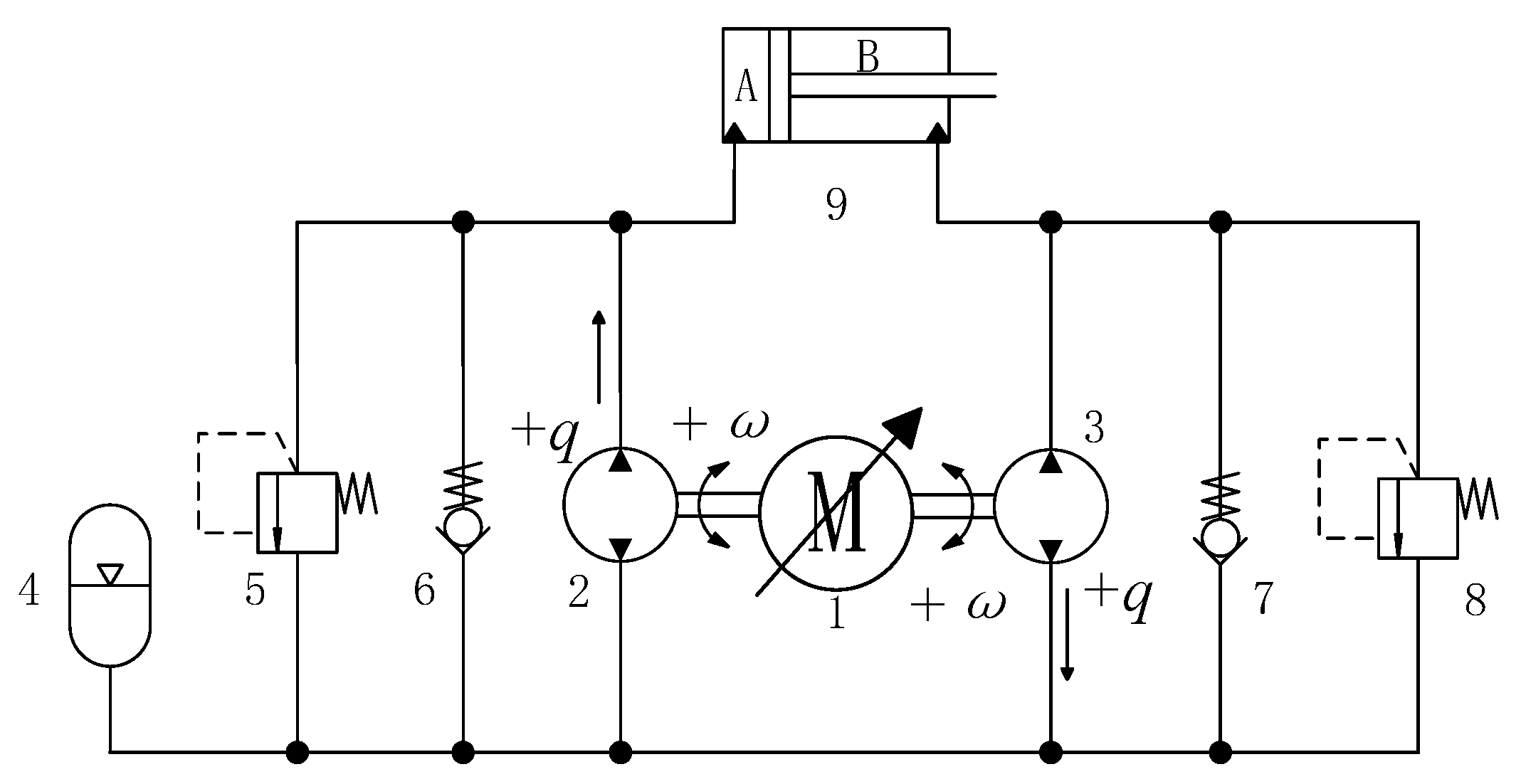
The DDH is mainly composed of a permanent magnet synchronous motor, two bi-directional pumps, a hydraulic accumulator, two check valves, and two pressure relief valves, as shown in Figure 1 and

Table 1. List of components (see Figure 1).

No.	Component	No.	Component
1	Permanent magnet synchronous motor	5, 8	Pressure relief valve
2	A-side pump	6, 7	Check valve
3	B-side pump	9	Hydraulic cylinder
4	Hydraulic accumulator

. The two pumps are driven by a permanent magnet synchronous motor, the hydraulic accumulator is installed between the two pumps to make the system more compact, two check valves are used to prevent cavitation, and two pressure relief valves are used for safety purposes.

2.2. DDH Model

The DDH models mainly include the pump and cylinder. In the model, the following assumptions are given: the hydraulic cylinder leakage is zero, the hydraulic cylinder load is an inertial load, and there is no elastic load.

2.2.1. Pump Model

The flow equation of the pump is given by

$$Q_{\mathrm{A}}=\eta \omega D_{\mathrm{pA}}$$

(1)

$$Q_{\mathrm{B}}=-\eta \omega D_{\mathrm{pB}}$$

(2)

where $\eta$ is the volumetric efficiency of the pump, and it is set to be 85%; $\omega$is the angular velocity, $D_{\mathrm{p}}$ is the volumetric displacement.

2.2.2. Cylinder Model

The flow equation of the hydraulic cylinder can be expressed by

$$q_{\mathrm{A}}=A_{\mathrm{A}}\dot{x}+\frac{V_1}{{{\displaystyle \beta }}_{\mathrm{e}}}{{\displaystyle \dot{p}}}_{{}_{\mathrm{A}}}$$

(3)

$$-q_{\mathrm{B}}=A_{\mathrm{B}}\dot{x}+\frac{V_2}{{{\displaystyle \beta }}_{\mathrm{e}}}{\dot{p}}_{\mathrm{B}}$$

(4)

$$V_1=V_{10}+A_{\mathrm{A}}x$$

(5)

$$V_2=V_{20}+A_{\mathrm{B}}x$$

(6)

where $q_A$ and $q_{\mathrm{B}}$ are the flow of the chamber A and chamber B, $A_{\mathrm{A}}$ is the piston area, $A_{\mathrm{B}}$ is the difference in piston and piston rod area, x is the absolute position of the piston $p_{\mathrm{A}}$ and $p_{\mathrm{B}}$ are the pressures of chamber A and chamber B, ${\beta }_{\mathrm{e}}$ is the effective bulk modulus, $V_1$ and $V_2$ is the total volume of chamber A and chamber B, $V_{10}$ and $V_{20}$ are”dead volume” of chamber A and chamber B.

Hydraulic cylinder force balance equation can be expressed by

$${{\displaystyle p}}_{\mathrm{A}}{{\displaystyle A}}_1-{{\displaystyle p}}_{\mathrm{B}}{{\displaystyle A}}_2=M\ddot{x}+B_{\mathrm{c}}\dot{x}+F$$

(7)

where $B_{\mathrm{c}}$ is damping coefficient,$F$ is the random external load force.

2.2.3. State-Space Equation

Defining the state variables $[x_1,x_2,x_3]=[x,\dot{x},\ddot{x}]$, based on Equations (1)–(7), the system state-space equations can be represented as

$$\{\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=x_3\\ {\dot{x}}_3=k_1{x}_2+k_2{x}_3+k_3\omega +f\end{array}$$

(8)

where

$$k_1=-(\frac{A{}_1{}^2{\beta }_{\mathrm{e}}}{V_{1}m}-\frac{A_2{}^2{\beta }_{\mathrm{e}}}{V_{2}m});k_2=-\frac{B_{\mathrm{c}}}{m};k_3=\frac{A_1\eta D_{\mathrm{pA}}{\beta }_{\mathrm{e}}}{V_{1}m}-\frac{A_2\eta D_{\mathrm{pB}}{\beta }_{\mathrm{e}}}{V_{2}m};f=-\frac{{\dot{F}}_{\mathrm{L}}}{m}.$$

2.2.4. Mechanical Model of the Micro-Crane

The schematic diagram of the crane structure is shown in Figure 2.

The load force acts on the end of the crane structure and generates torque around the joint Θ. The torque balance equation is displayed as follows

$${\displaystyle \sum M_{\text{θ}}=J\frac{d^2\theta }{d{t}^2}}$$

(9)

$$\frac{d^2\theta }{d{t}^2}=(\frac{1}{J})[(-m_1\cdot r_1\cdot \sin ({\theta }_{\mathrm{m}1})-m_2\cdot r_2\cdot \sin ({\theta }_{\mathrm{m}2})-m_{\mathrm{load}}\cdot \sin ({\theta }_{\mathrm{mload}}))g+F_{\mathrm{Cyl}}\cdot \sin (\alpha )\cdot d_1]$$

(10)

where $F_{\mathrm{Cyl}}$ is the net hydraulic force, g is the gravitational constant, α is the angle between the cylinder and the boom, $m_{\mathrm{i}}$ is a mass, $d_1$and $d_2$ are the distance to the upper fastening point of the cylinder, ${\theta }_{\mathrm{i}}$ are the angles between the centre of mass and the vertical axis.

The angles $\gamma$,${\theta }_{\mathrm{m}1}$, ${\theta }_{\mathrm{m}2}$,and ${\theta }_{\mathrm{mload}}$ shown in Figure 2 can be determined by adding the change of θ to the measured value when the hydraulic cylinder is fully retracted

$$\gamma ={\gamma }_0+{\displaystyle {\int }_0^{\mathrm{t}}\frac{d\theta }{dt}dt}$$

(11)

$${\theta }_{\mathrm{m}1}={\theta }_{\mathrm{m}10}+{\displaystyle {\int }_0^{\mathrm{t}}\frac{d\theta }{dt}dt}$$

(12)

$${\theta }_{\mathrm{m}2}={\theta }_{\mathrm{m}20}+{\displaystyle {\int }_0^{\mathrm{t}}\frac{d\theta }{dt}dt}$$

(13)

$${\theta }_{\mathrm{mload}}={\theta }_{\mathrm{mload}0}+{\displaystyle {\int }_0^{\mathrm{t}}\frac{d\theta }{dt}dt}$$

(14)

Use the sine rule given below to obtain the angle$\alpha$

$$\sin (\alpha )=\frac{d_2}{x_{\mathrm{t}}}\sin (\gamma )$$

(15)

where $d_2$ is the distance to the fastening point on the cylinder, and $x_{\mathrm{t}}$ is the length of the cylinder plus the stroke of the piston. $x_{\mathrm{t}}$ is derived using the cosine rule

$$x_{\mathrm{t}}{}^2=d_1{}^2+d_2{}^2-2d_1{d}_2\cos (\gamma )$$

(16)

According to the derivation of Equation (16), the hydraulic cylinder velocity can be expressed by

$$\frac{d{x}_{\mathrm{t}}}{dt}=\frac{d_1{d}_2\frac{d\gamma }{dt}\sin (\gamma )}{\sqrt{d_1{}^2+d_2{}^2-2d_1{d}_2\cos (\gamma )}}$$

(17)

2.2.5. Model Validation

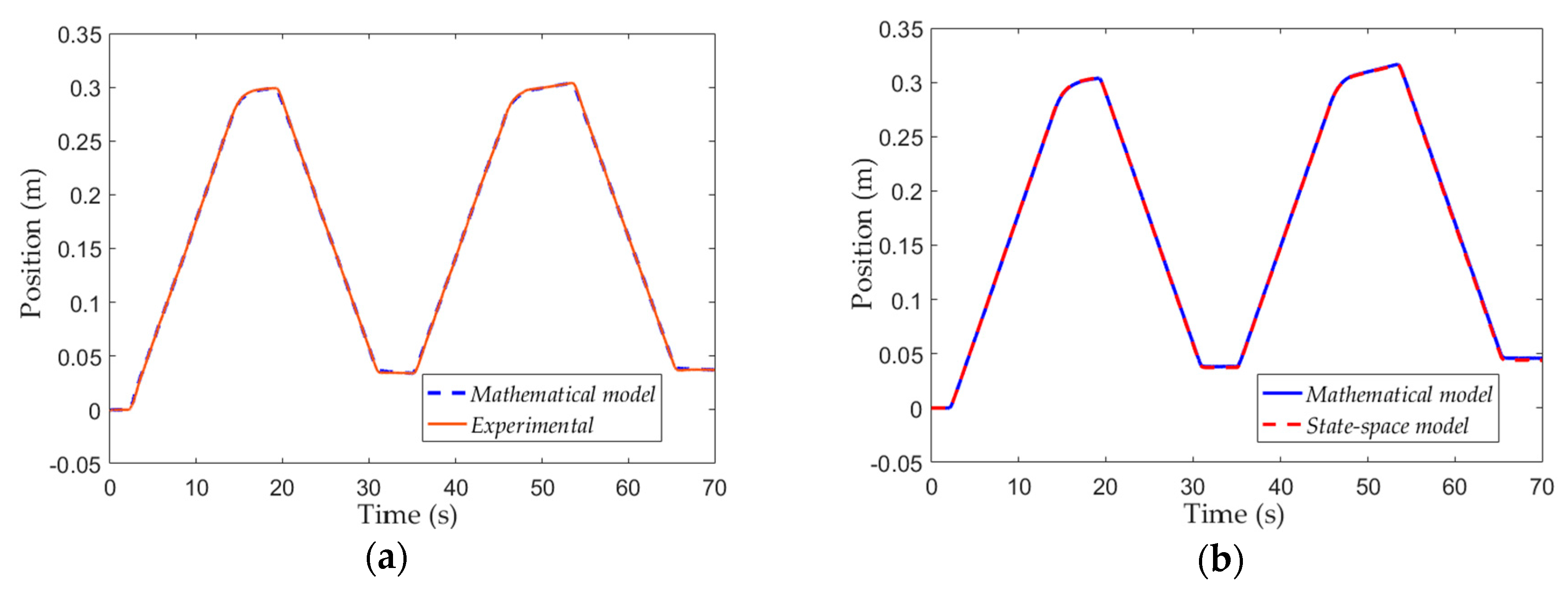
This subsection verifies the feasibility of the deduced state-space equation of the DDH. The parameters of the DDH are shown in

Table 2. Simulation parameters of DDH.

Parameters	Value	Unit	Parameters	Value	Unit
Pump A Volumetric Displacement (DpA)	13.03	mL/rev	Effective bulk modulus (βe)	7 × 108	Pa
Pump B Volumetric Displacement (DpB)	9.35	mL/rev	Cylinder stroke (L)	400	mm
Piston diameter of hydraulic cylinder (dd)	60	mm	Damping coefficient (Bc)	500	N·s/m
Piston rod diameter of hydraulic cylinder (dr)	30	mm	Dead volume of chamber A (V01)	2 × 10−6	m3
Load mass (m)	50	kg	Dead volume of chamber B (V02)	2 × 10−6	m3

. Firstly, the experimental data from reference [10] is used to verify the accuracy of the mathematical model of DDH. The comparison between the simulation results of the mathematical model and the experimental results show that the position curve is basically consistent, as shown in Figure 3a. Then, the simulation was performed using the state-space model, and the result is shown in Figure 3b. The position curve of the state-space model almost overlaps the other (mathematical model), which indicates that the created state-space model has acceptable accuracy for the design of the ADRC controller.

3. Design of ADRC

ADRC is a control algorithm without dependence on the system model. Its basic idea is to consider unmodelled dynamics and unknown external disturbance as “total disturbance” of the system. Further, the total disturbance is estimated and compensated. ADRC is mainly composed of three parts: the tracking differentiator (TD), the extended state observer (ESO), and the nonlinear feedback control law (NFCL) [20,21]. 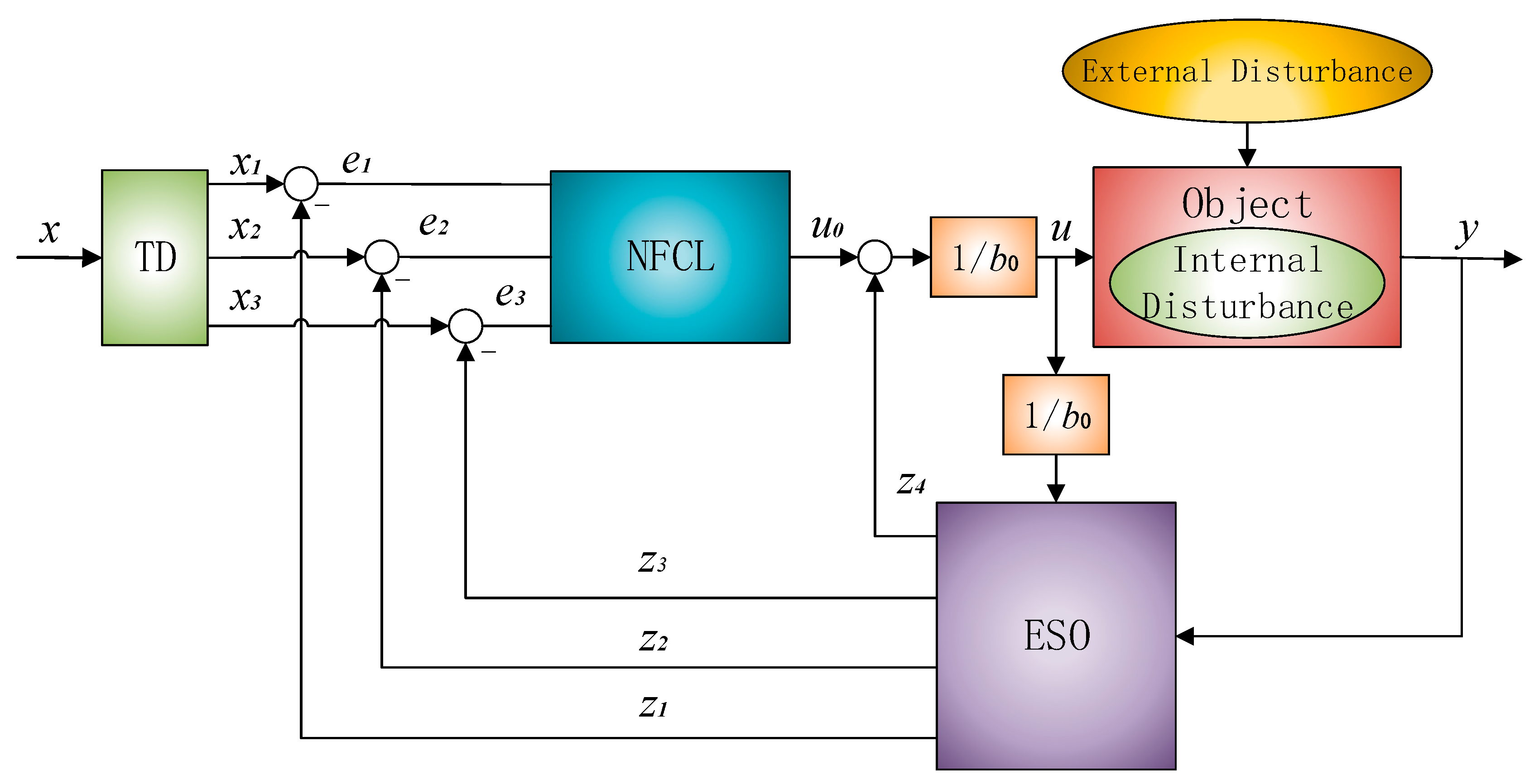Figure 4 illustrates the structure of ADRC. TD is used to arrange the transition process, and the input signal x₁ passes through the TD to give the differential signals: x₂ and x₃; ESO is used to give the estimated value of the state variables and total disturbance; z₁, z₂, z₃ is the estimated value of the state; z₄ is the estimated value of the total disturbance; NFCL is used to nonlinearly combine the error between the transition process and the estimated state variables to achieve nonlinear control strategy; e₁, e₂, e₃ is the deviation signal; b₀ is the compensation factor; y is the output signal.

3.1. Design of TD

TD is actually a signal processing; it can closely track the input signal and give the differential signal of the input signal. Thus, it is possible to reduce the initial error of the system and avoid overshooting caused by the sudden change in setting value [20,21]. The DDH adopts a three-order TD, and the discrete forms can be represented as follows

$$\{\begin{array}{l}fh=fhan(x_1(k),x_2(k),r,h);\\ x_1(k+1)=x_1(k)+T{x}_2(k);\\ x_2(k+1)=x_2(k)+Tfh;\\ x_3(k+1)=fh\end{array}$$

(18)

where r is the speed factor, T is the sampling period, h is the filtering factor for the input signal; $f\left(x_1\left(k\right),x_2\left(k\right),r,h\right)$ is the fast optimal control function, and its definition is as follows

$$\{\begin{array}{l}fsg(x,d)=(sign(x+d)-sign(x-d))/2\\ d=r{h}^2\\ a_0=h{x}_2\\ y=x_1+a_0\\ a_1=\sqrt{d(d+8\left|y\right|)}\\ a_2=a_0+sign(y)(a_1-d)/2\\ a=(a_0+y)fsg(y,d)+a_2(1-fsg(y,d))\\ fhan=-r(\frac{a}{d})fsg(a,d)-rsign(a)(1-fsg(a,d))\end{array}$$

(19)

3.2. Design of ESO

The ESO is the core part of ADRC, which can track the state variables and estimate the internal and external disturbance of the system without the need for any precise mathematical model. The DDH uses a four-order ESO.

Let $m_{\mathrm{n}},B_{\mathrm{cn}},{\beta }_{\mathrm{en}}$ be the nominal values of $m,B_{\mathrm{c}},{\beta }_{\mathrm{e}}$, respectively, and then can be expressed by

$$k_{1\mathrm{n}}=-(\frac{A{}_1{}^2{\beta }_{\mathrm{en}}}{V_1{m}_{\mathrm{n}}}-\frac{A_2{}^2{\beta }_{\mathrm{en}}}{V_2{m}_{\mathrm{n}}})$$

(20)

$$k_{2\mathrm{n}}=-\frac{B_{\mathrm{cn}}}{m_{\mathrm{n}}}$$

(21)

$$k_{3\mathrm{n}}=\frac{A_1\eta D_{\mathrm{pA}}{\beta }_{\mathrm{en}}}{V_1{m}_{\mathrm{n}}}-\frac{A_2\eta D_{\mathrm{pB}}{\beta }_{\mathrm{en}}}{V_2{m}_{\mathrm{n}}}$$

(22)

$$f=-\frac{{\dot{F}}_{\mathrm{L}}}{m_{\mathrm{n}}}$$

(23)

Let $\tilde{a}$ be the difference between the nominal value and the actual value of the parameter, $\tilde{k}=k_n-k$, then Equation (8) can be rewritten as

$$\{\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=x_3\\ {\dot{x}}_3=k_{1\mathrm{n}}{x}_2+k_{2\mathrm{n}}{x}_3+k_{3\mathrm{n}}\omega +\sigma \end{array}$$

(24)

where $\sigma ={\tilde{k}}_1{x}_2-{\tilde{k}}_2{x}_3-{\tilde{k}}_3\omega +f$ represents the total disturbance of the system; in order to estimate the total disturbance, defining $x_4=\sigma$ as an extended state variable of the system, and assuming that $\sigma$ is differentiable, the system can be expressed by

$$\{\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=x_3\\ {\dot{x}}_3=a_{1\mathrm{n}}{x}_2+a_{2\mathrm{n}}{x}_3+x_4+a_{3\mathrm{n}}\omega \\ {\dot{x}}_4=f(x,t)\end{array}$$

(25)

where $f\left(x,t\right)$ represents the change rate of $\sigma$.

Let $\dot{z}=\left[{\dot{z}}_1,{\dot{z}}_2,{\dot{z}}_3,{\dot{z}}_4\right]$ be the estimated vector of state x, then the ESO is designed as

$$\{\begin{array}{l}{e}_1=z_1-y\\ \\ {\dot{z}}_1=z_2-{\beta }_{01}{e}_1\\ {\dot{z}}_2=z_3-{\beta }_{02}{e}_1\\ {\dot{z}}_3=a_{1n}{z}_2+a_{2n}{z}_3+z_4-{\beta }_{03}{\left|e_1\right|}^{\frac{1}{4}}sign(e_1)+a_{3n}\omega \\ {\dot{z}}_4=-{\beta }_{04}{\left|e_1\right|}^{\frac{1}{8}}sign(e_1)\end{array}$$

(26)

Observer gain is simplified according to the bandwidth concept from reference [22].

$${\beta }_{01}=4\omega ,{\beta }_{02}=6{\omega }^2,{\beta }_{03}=4{\omega }^3,{\beta }_{04}={\omega }^4$$

3.3. Design of NFCL

Using the fastest control synthesis function fhan to perform nonlinear combination of errors, the algorithm can be expressed by

$$\{\begin{array}{l}{e}_1=x_1-z_1\\ e_2=x_2-z_2\\ e_3=v_3-z_3\\ u_0={\beta }_{1}fal(e_1,\alpha ,\delta )+{\beta }_{2}fal(e_2,\alpha ,\delta )+{\beta }_{3}fal(e_3,\alpha ,\delta )\\ \\ u=u_0-\frac{z_4}{b_0}.\end{array}$$

(27)

4. Simulation Results and Analysis

This section combines the DDH model, the micro-crane mechanical model, and the designed ADRC method into one model, uses sine signal and actual working position signal as inputs to the system, and compares the position tracking performance with P and PI controller. The simulation parameters of DDH are shown in Table 2, and the parameters of the micro-crane are shown in

Table 3. Micro-crane structure parameters.

Parameters	Value	Unit
d1	0.983	m
m1	25.11	kg
m2	21.40	kg
mload	40	kg
r2	0.977	m
rload	1.674	m
θm10	0.1169	rad
θm20	0.1572	rad
θmload	0.1775	rad

.

4.1. Sine Signal

In order to test the performance of the adopted control method, the sine position signal was set as Equation (28), and the tracking performance of ARDC was analyzed with or without disturbance. The simulation result without disturbance is shown in Figure 5.

$$x_r=0.15\sin (\frac{2}{10}\pi t-\frac{\pi }{2})+0.15$$

(28)

The working process of the hydraulic system is often accompanied by the disturbance of the external load force. In order to compare the tracking performance and robustness with different control methods, a sudden disturbance force is added. The control tracking effect is shown in Figure 6.

As shown in Figure 5 and Figure 6,

Table 4. Comparison of tracking error of sine position signal.

Control Method	Without Disturbance Position Error/m		With Disturbance Position Error/m
	Root Mean Square	Maximum	Root Mean Square	Maximum
P	2.985 × 10−3	5.132 × 10−3	3.472 × 10−3	5.275 × 10−3
PI	1.262 × 10−3	2.080 × 10−3	1.223 × 10−3	2.081 × 10−3
ADRC	4.276 × 10−4	1.514 × 10−3	3.833 × 10−4	1.514 × 10−3

, without disturbance, the maximum errors of P control and PI control are 5.132 and 2.080 mm. In contrast, the maximum error of ADRC is 1.514 mm. It can be seen that the maximum tracking error is reduced by about 70% and 27%, and the root means that square error is reduced by about 86% and 66%, respectively. With disturbance, the maximum errors of P control and PI control are 5.275 and 2.081 mm. In contrast, the maximum error of ADRC is 1.514 mm. The maximum tracking error is reduced by about 71% and 27%, and the root means that square error is reduced by about 89% and 69%, respectively. It can be seen that, with ADRC, certain fluctuations appear at the beginning, but this will converge quickly. The position tracking error shown in Figure 5b and Figure 6c reveals that the ADRC suppresses internal and external disturbances effectively, with high position tracking precision and strong robustness.

4.2. Actual Working Position Signal

The simulation was carried out using the actual working position signal as input, and the simulation result without disturbance is shown in Figure 7.

Further, the simulation was carried out with disturbance to compare the tracking performance and robustness with varying control methods. The simulation result with disturbance is shown in Figure 8.

As shown in Figure 7 and Figure 8,

Table 5. Comparison of tracking error of actual working position signal.

Control Method	Without Disturbance Position Error/m		With Disturbance Position Error/m
	Root Mean Square	Maximum	Root Mean Square	Maximum
P	2.415 × 10−3	3.829 × 10−3	2.642 × 10−3	4.189 × 10−3
PI	1.955 × 10−3	5.221 × 10−3	1.873 × 10−3	5.221 × 10−3
ADRC	5.268 × 10−4	2.183 × 10−3	5.003 × 10−4	2.183 × 10−3

, without disturbance, the maximum errors of P control and PI control are 3.829 and 5.221 mm. In contrast, the maximum error of ADRC is 2.193 mm, the maximum tracking error is reduced by about 43% and 58%, and the root means square error is reduced by about 78% and 73%, respectively. With disturbance, the maximum errors of P control and PI control are 4.189 and 5.221 mm. In contrast, the maximum error of ADRC is 2.183 mm. The maximum tracking error is reduced by about 48% and 58%, and the root means square error is reduced by about 81% and 73%, respectively. The position tracking error shown in Figure 7b and Figure 8c reveals that the ADRC suppresses internal and external disturbances effectively, with high position tracking precision and strong robustness.

In summary, the simulation results show that the proposed ADRC control method has better tracking performance and stronger robustness.

5. Conclusions

Aiming towards the problems of uncertain parameters and unknown external disturbances in the DDH, an ADRC controller was designed. The control method can estimate the total disturbance, including parameter uncertainty and unknown disturbance, and provide compensation. A model was built, including the DDH, mechanism of the crane, and ADRC controller. Simulations were performed using two types of reference signal. The simulation results reveal that, without disturbance, compared with the P and PI control, ADRC can reduce the maximum error by about 43% and 58%, and can decrease the root means square error by about 78% and 73%. With disturbance, compared with P and PI control, ADRC reduces the maximum error by about 48% and 58%, and decrease the root means square error by about 81% and 73%. The results show that, compared with PID control, ADRC can suppress internal and external disturbances effectively, has the advantage of robustness, and improves the position tracking precision.

Although the control method ADRC can improve control accuracy on the DDH based on the simulation results, it should be compared with experimental data for validation. Hence, in the near future, a test bench needs to be set up, and experiments should be performed with the proposed control method.