Energetic Sustainability of Systems †
Abstract
1. Introduction
2. Methods
- one should create a system model to be used to investigate the problem;
- the problem of closed systems should be investigated. Based on this, a conclusion can be drawn for singular cases;
- a test model should be developed in which only two systems have an ideal relationship. This constitutes the general dual system testing model. It should examine the relationship between structurally different systems:
- the dual relationship of rigid systems must be examined;
- the dual relationship between fully flexible systems needs to be examined;
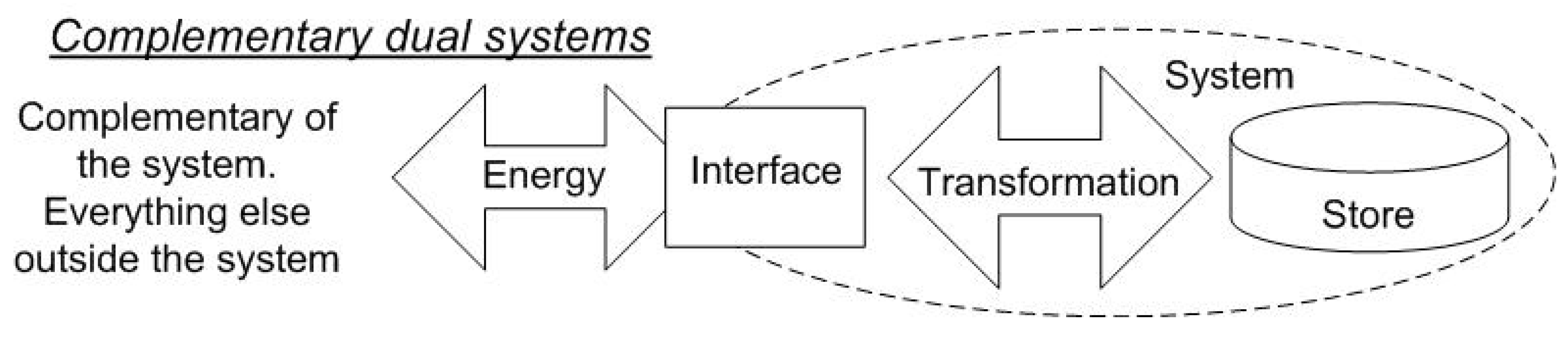
- in the dual test model, one system must be replaced with the complement of the other system.
3. Results
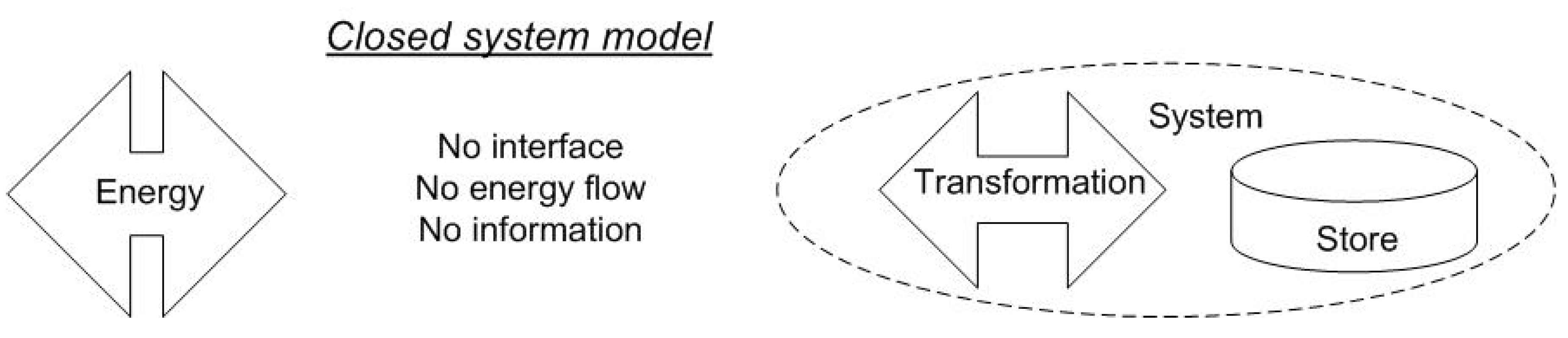
- modeling of perfectly closed systems is only possible in theory, their existence cannot be proved,
- completely rigid systems engulf each other;
- perfectly flexible systems are balanced;
- the energy condition for sustainability is the continuous and unlimited growth of stored energy. This result is consistent with the experience that the energy of the long-life systems increases exponentially.
4. Discussion
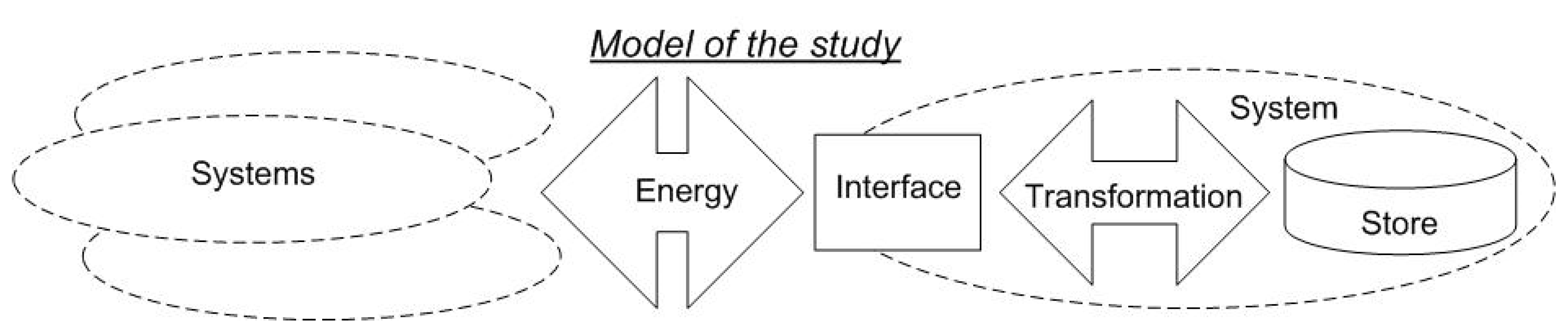
4.1. Model
4.2. Closed Systems
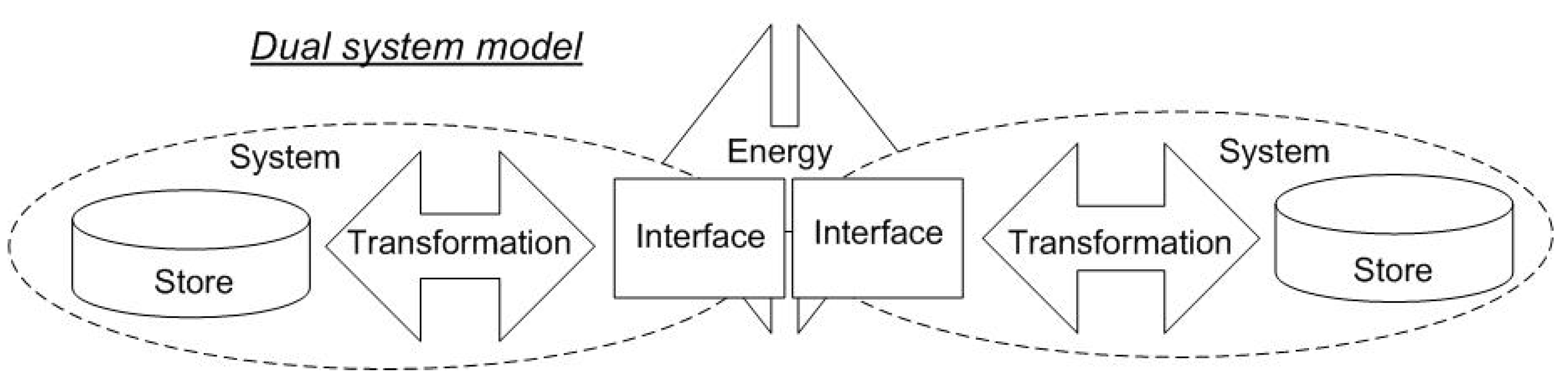
4.3. Dual Systems
4.4. Rigid Dual Systems
4.5. Flexible Dual Systems
4.6. Complementary Dual Systems
5. Summary
Funding
References
- Bernardi, D.; Pawlikowski, E.; Newman, J. A General Energy Balance for Battery Systems. J. Electrochem. Soc. 1985, 132, 5–12. [Google Scholar] [CrossRef]
- Kasac, J.; Stefancic, H.; Stepanic, J. Comparison of social and physical free energies on a toy model. Phys. Rev. E 2004, 1, 16117–16124. [Google Scholar] [CrossRef] [PubMed]
- Albini, A.; Rajnai, Z. Modeling general energy balance of systems. Procedia Manuf. 2019, 32, 374–379. [Google Scholar] [CrossRef]
- Tokody, D.; Schuszter, G.; Papp, J. Study of How to Implement an Intelligent Railway System in Hungary. In Proceedings of the 2015 IEEE 13th International Symposium on Intelligent Systems and Informatics (SISY), Subotica, Serbia, 17–19 September 2015; Szakál, A., Ed.; IEEE: New York, NY, USA, 2015. [Google Scholar]
- Kiss, M.; Breda, G.; Muha, L. Information security aspects of Industry 4.0. Procedia Manuf. 2019, 32, 848–855. [Google Scholar] [CrossRef]
- Tokody, D. Digitising the European industry-holonic systems approach. Procedia Manuf. 2018, 22, 1015–1022. [Google Scholar] [CrossRef]
- Szabó, Z. The effects of globalization and cyber security on smart cities. Interdiscip. Descr. Complex Syst. 2019, 17, 503–510. [Google Scholar] [CrossRef]
- Kovács, Z. Cloud Security in Terms of the Law Enforcement Agencies. Hadmérnök 2012, 7, 144–156. [Google Scholar]
- Mester, G. Rankings Scientists, Journals and Countries Using h-index. Interdiscip. Descr. Complex Syst. 2016, 14, 1–9. [Google Scholar] [CrossRef]
- Dobrilovic, D.; Odadzic, B. Virtualization Technology as a Tool for Teaching Computer Networks. Int. J. Educ. Pedagog. Sci. 2008, 13, 41–45. [Google Scholar]
- Mester, G. Academic Ranking of World Universities 2009/2010. IPSI J. Trans. Internet Res. TIR 2011, 7, 44–47. [Google Scholar]
- Albini, A.; Tokody, D.; Rajnai, Z. Theoretical Study of Cloud Technologies. Interdiscip. Descr. Complex Syst. 2019, 17, 511–519. [Google Scholar] [CrossRef]
- Albini, A.; Rajnai, Z. General Architecture of Cloud. Procedia Manuf. 2018, 22, 485–490. [Google Scholar] [CrossRef]
- Albini, A.; Mester, G.; Iantovics, B.L. Unified Aspect Search Algorithm. Interdiscip. Descr. Complex Syst. 2019, 17, 20–25. [Google Scholar] [CrossRef]
- Mester, G. Obstacle Avoidance and Velocity Control of Mobile Robots. In Proceedings of the 6th International Symposium on Intelligent Systems and Informatics SISY 2008, Subotica, Serbia, 26–27 September 2008; Catalog Number CFP0884C-CDR. IEEE: Piscataway, NJ, USA, 2008; pp. 97–101. [Google Scholar]
- Mester, G.; Rodic, A. Sensor-Based Intelligent Mobile Robot Navigation in Unknown Environments. Int. J. Electr. Comput. Eng. Syst. 2010, 1, 55–66. [Google Scholar]
- Szabó, A.; Szucs, E.; Berek, T. Illustrating Training Opportunities Related to Manpower Facility Protection through the Example of Máv Co. Interdiscip. Descr. Complex Syst. 2018, 16, 320–326. [Google Scholar] [CrossRef]
- Mester, G.; Pletl, S.; Pajor, G.; Basic, D. Adaptive Control of Rigid-Link Flexible-Joint Robots. In Proceedings of the 3rd International Workshop of Advanced Motion Control, Berkeley, CA, USA, 20–23 March 1994; pp. 593–602. [Google Scholar]
- Mester, G.; Pletl, S.; Nemes, A.; Mester, T. Structure Optimization of Fuzzy Control Systems by Multi-Population Genetic Algorithm. In Proceedings of the 6th European Congress on Intelligent Techniques and Soft Computing, EUFIT’98, Aachen, Germany, 7–10 September 1998; Verlag Mainz: Aachen, Germany, 1998; pp. 450–456. [Google Scholar]
- Mester, G.; Rodic, A. Simulation of Quad-rotor Flight Dynamics for the Analysis of Control, Spatial Navigation and Obstacle Avoidance. In Proceedings of the 3rd International Workshop on Advanced Computational Intelligence and Intelligent Informatics (IWACIII 2013), Shanghai, China, 18–21 October 2013; pp. 1–4. [Google Scholar]
- Zamfirescu, C.B.; Duta, L.; Iantovics, L.B. The Cognitive Complexity in Modelling the Group Decision Process. BRAIN Broad Res. Artif. Intell. Neurosci. 2010, 1, 69–79. [Google Scholar]
- Shatnawi, M.M. Applying Information Security Risk Management Standards Process for Automated Vehicles. Bánki Rep. 2019, 2, 70–74. [Google Scholar]
- Albininé Budavári, E.; Rajnai, Z. The Role of Additional Information in Obtaining information. Interdiscip. Descr. Complex Syst. 2019, 17, 438–443. [Google Scholar] [CrossRef]
- Hell, P.M.; Varga, P.J. Drone systems for factory security and surveillance. Interdiscip. Descr. Complex Syst. 2019, 17, 458–467. [Google Scholar] [CrossRef]
- Pető, R. Security of Smart City. Interdiscip. Descr. Complex Syst. 2019, 1, 13–19. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albini, A.; Budavári, E.A.; Rajnai, Z. Energetic Sustainability of Systems. Proceedings 2020, 63, 50. https://doi.org/10.3390/proceedings2020063050
Albini A, Budavári EA, Rajnai Z. Energetic Sustainability of Systems. Proceedings. 2020; 63(1):50. https://doi.org/10.3390/proceedings2020063050
Chicago/Turabian StyleAlbini, Attila, Edina Albininé Budavári, and Zoltán Rajnai. 2020. "Energetic Sustainability of Systems" Proceedings 63, no. 1: 50. https://doi.org/10.3390/proceedings2020063050
APA StyleAlbini, A., Budavári, E. A., & Rajnai, Z. (2020). Energetic Sustainability of Systems. Proceedings, 63(1), 50. https://doi.org/10.3390/proceedings2020063050




