Selecting the Optimal Use of the Geothermal Energy Produced with a Deep Borehole Heat Exchanger: Exergy Performance †
Abstract
:1. Introduction
2. Materials and Methods
- Undisturbed/far-field ground temperature: the ground source is, as a precautionary measure, assumed to act as a purely conductive media. The far-field ground temperature profile is assumed to act as a linear function of the depth with a surface value of 25 °C (reference ambient temperature) and a constant temperature gradient over the z-direction, Kg. The values of Kg, and αg are the objectives of the next sensitivity analysis.
- WBHX: the thermal power exchanged between the circulating fluid and the far-field ground temperature is evaluated through a series of equivalent thermal resistances. The axial effects are neglected, however, and the temperature evolution of the fluid along the WHBX ducts is evaluated through the so-called “quasi-3D approach” [36,39]. At a given depth, z, the following differential equation applies:
- District heating: the district heating network is modelled as a water flow to be heated from 60 to 90 °C. The useful flow rate, mDH, and the corresponding thermal power are calculated considering a heat transfer effectiveness of the main DH heat exchanger equal to 0.8. The DH application is only considered if the production temperature of the WBHX must be higher than 100 °C.
- Absorption chiller: the end-user chiller loop works with supply and return temperatures of 7 and 12 °C, respectively. The chiller is assumed to act as an indirect-fired unit, namely the generator is equipped with a heat exchanger that allows the energy transfer between the hot water from the WBHX loop and the refrigerant mixture (e.g., LiBr-H2O). The temperature required at the generator, Tgen, is assumed equal to 100 °C. The heat exchanger within the ABSC generator is assumed to be sufficiently long to ensure a unitary heat transfer effectiveness: in other words, the WBHX fluid leaves the absorption unit with a temperature equal to the one required in the ABSC generator. The performance of the chiller is evaluated through the second law of thermal efficiency method, according to source temperatures and exergy efficiency, ηIIABSC, assumed as constant and equal to 0.3.
- ORC power plant and cooling tower: following the results presented in [36], the considered working fluid is 2-methylpropane (isobutane). Depending on the temperature at the WBHX outlet section, the power of the Hirn cycle is calculated using the following assumption: a condenser temperature equal to 41 °C; a pinch point of the HRSG equal to 5 K; an approach point for all the heat exchangers equal to 10 K; an isentropic and electrical-mechanical efficiency of the turbine equal to 0.85 and 0.95, respectively; and an electrical-mechanical efficiency of the feeding pump equal to 0.6. The power required by the fans in the cooling tower is evaluated according to the model presented in the Appendix of [36]. For each tested configuration, the geometry of the finned surface (i.e., number of rows and number of ducts per row) and the frontal air velocity are optimized to minimize the electricity input, ensuring the required heat exchange at the condenser.
- Thermal diffusivity of the ground: αg = {10−7; 5 × 10−7; 10−6} m2/s
- Thermal conductivity of the ground source: λg = {1; 2; 3} W/(m K)
- Ground temperature gradient: Kg = {30; 60; 90; 120; 150} K/km
- WBHX depth: H = {1, 2, 3, 4, 5} km.
- The WBHX fluid must be in the liquid state. Proper work pressure and flow rate are thus evaluated for each configuration.
- The ground temperature at the well bottom must be higher than 100 °C.
- Configurations resulting in negative exergy efficiency are discarded (e.g., when the auxiliary energy consumption exceeds the power production).
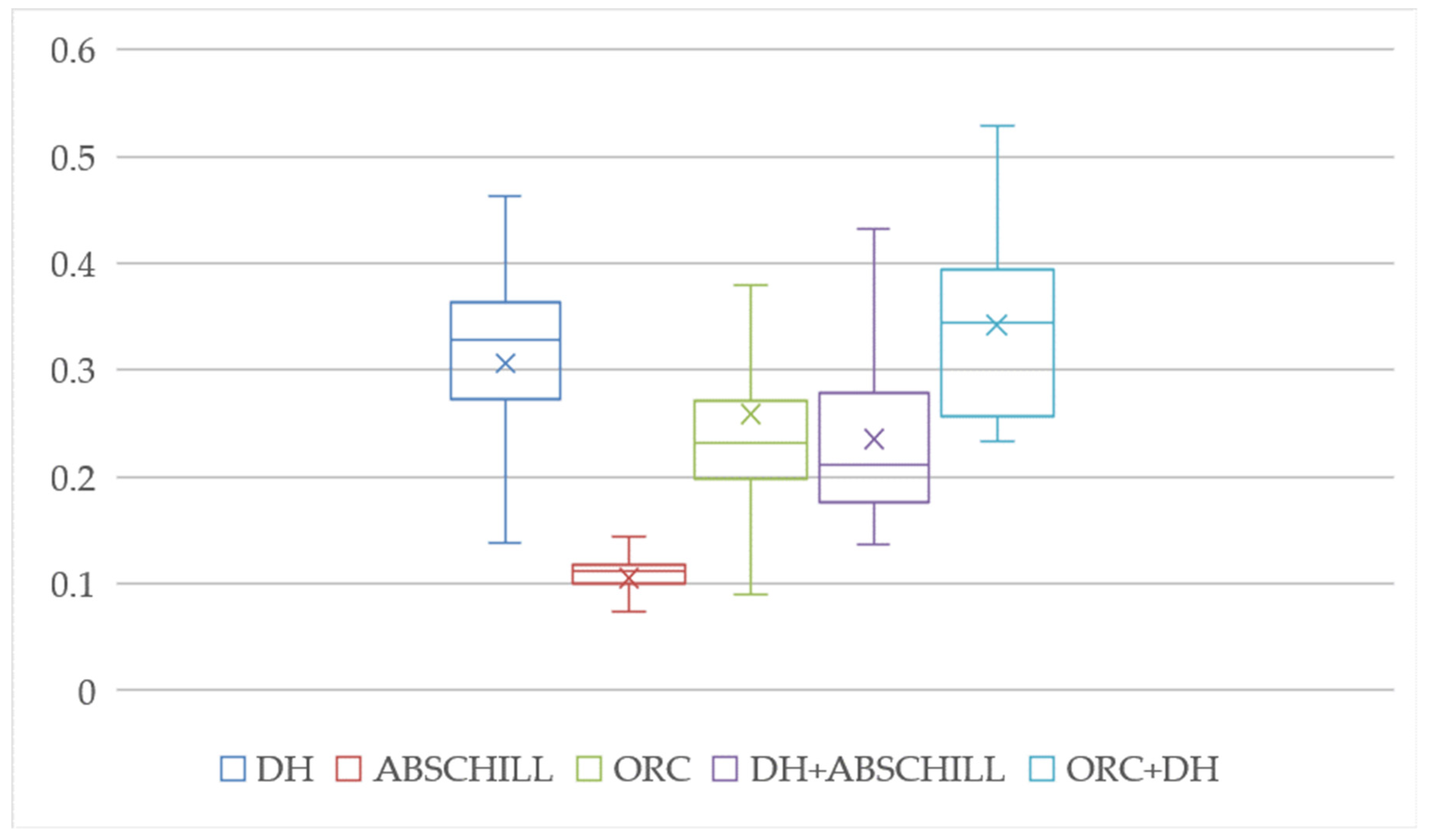
3. Results
4. Discussion and Conclusions
Conflicts of Interest
Nomenclature
| c | specific heat capacity | [J/kg K] |
| specific exergy | [kJ/kg] | |
| exergy rate | [W] | |
| Kg | temperature gradient | [°C/100 m] |
| exergy destruction | [W] | |
| IQR interquartile range | ||
| k | convective heat transfer | [W/m2 K] |
| H | total length of the well | [m] |
| mass flow rate | [kg/s] | |
| p | pressure | [bar, MPa] |
| total thermal power | [W] | |
| R | thermal resistance | [mK/W] |
| r | radius | [mm] |
| T | temperature | [K or °C] |
| t | time | [s] |
| mechanical/electrical power | [W] | |
| z | depth | [m] |
Greek symbols
| α | thermal diffusivity | [m2/s] |
| η | efficiency | |
| λ | thermal conductivity | [W/m K] |
| ρ | density | [kg/m3] |
Subscripts, superscripts, acronyms
| a | ambient state |
| ABSC | absorption chiller |
| CP | circulation pump |
| CT | cooling tower |
| DH | district heating |
| DSH+COND | desuperheater + condenser |
| dw | downward |
| EER | energy efficiency ratio |
| EVA | evaporator |
| f | fluid |
| gen | generator |
| HEx | heat-exchanger |
| II | second-law |
| i | inner |
| in | inlet |
| o | outer |
| ORC | organic Rankine cycle |
| out | outlet |
| P | pump |
| PH | preheater |
| ret | return |
| s | soil property |
| sup | supply |
| SH | superheater |
| T | turbine |
| up | upward |
| w | water |
| WBHX | WellBore Heat eXchanger |
| 0 | reference state |
References
- IRENA. Renewable Capacity Statistics 2019; International Renewable Energy Agency (IRENA): Abu Dhabi, UAE, 2019; ISBN 978-92-9260-123-2. [Google Scholar]
- Kujawa, T.; Nowak, W.; Stachel, A.A. Utilization of existing deep geological wells for acquisitions of geothermal energy. Energy 2006, 31, 650–664. [Google Scholar] [CrossRef]
- Wang, Z.; McClure, M.W.; Horne, R.N. A single-well EGS configuration using a thermosiphon. In Proceedings of the Thirty-Fourth Workshop on Geothermal Reservoir Engineering Stanford University, Stanford, CA, USA, 9–11 February 2009. [Google Scholar]
- Taleghani, A.D. An improved closed-loop heat extraction method for geothermal resources. J. Energy Resour. Technol. ASME 2013, 135. [Google Scholar] [CrossRef]
- Akhmadullin, I.; Tyagi, M. Design and analysis of electric power production unit for low enthalpy geothermal reservoir applications. Int. J. Environ. Chem. Ecol. Geol. Geophys. Eng. 2014, 1, 6. [Google Scholar]
- Mokhtari, H.; Hadiannasab, H.; Mostafavi, M.; Ahmadibeni, A. Determination of optimum geothermal Rankine cycle parameters utilizing coaxial heat exchanger. Energy 2016, 102, 260–275. [Google Scholar] [CrossRef]
- Renaud, T.; Verdin, P.; Falcone, G. Numerical simulation of a Deep Borehole Heat Exchanger in the Krafla geothermal system. Int. J. Heat Mass Transf. 2019, 143, 118496. [Google Scholar] [CrossRef]
- Nalla, G.; Shook, G.M.; Mines, G.L.; Bloomfield, K.K. Parametric sensitivity study of operating and design variables in wellbore heat exchangers. Geothermics 2005, 34, 330–346. [Google Scholar] [CrossRef]
- Morita, K.; Bollmeier, W.S.; Mizogami, H. An experiment to prove the concept of the downhole coaxial heat exchanger (DCHE) in Hawaii. Trans. Geotherm. Res. Council 1992, 16, 9–16. [Google Scholar]
- Kohl, T.; Brenni, R.; Eugster, W. System performance of a deep borehole heat exchanger. Geothermics 2002, 31, 687–708. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, F.; Liu, J.; Ma, Z.; Han, E.; Song, M. Field test and numerical investigation on the heat transfer characteristics and optimal design of the heat exchangers of a deep borehole ground source heat pump system. Energy Convers. Manag. 2017, 153, 603–615. [Google Scholar] [CrossRef]
- Dai, C.; Shi, Y.; Zeng, L.; Li, J.; Lei, H. Heat Extraction Performance of a Deep Downhole Heat Exchanger. Energy Procedia 2019, 158, 5602–5607. [Google Scholar] [CrossRef]
- Galoppi, G.; Biliotti, D.; Ferrara, G.; Carnevale, E.A.; Ferrari, L. Feasibility study of a geothermal power plant with a double-pipe heat exchanger. Energy Procedia 2015, 81, 193–204. [Google Scholar] [CrossRef]
- Alimonti, C.; Soldo, E.; Berardi, D.; Bocchetti, D. A comparison between energy conversion systems for a power plant in Campi Flegrei geothermal district based on a WellBore Heat eXchanger. In Proceedings of the European Geothermal Congress 2016, Strasbourg, France, 19–23 September 2016. [Google Scholar]
- Alimonti, C.; Soldo, E. Study of geothermal power generation from a very deep oil well with a wellbore heat exchanger. Renew. Energy 2016, 86, 292–301. [Google Scholar] [CrossRef]
- Davis, A.P.; Michaelides, E.E. Geothermal power production from abandoned oil wells. Energy 2009, 34, 866–872. [Google Scholar] [CrossRef]
- Templeton, J.D.; Ghoreishi-Madiseh, S.A.; Hassani, F.; Al-Khawaja, M.J. Abandoned petroleum wells as sustainable sources of geothermal. Energy 2014, 70, 366–373. [Google Scholar] [CrossRef]
- Feng, Y.; Tyagi, M.; White, C.D. A downhole heat exchanger for horizontal wells in low-enthalpy geopressured geothermal brine reservoirs. Geothermics 2015, 53, 368–378. [Google Scholar] [CrossRef]
- Noorollahi, Y.; Pourarshad, M.; Jalilinasrabady, S.; Yousefi, H. Numerical simulation of power production from abandoned oil wells in Ahwaz oil field in southern Iran. Geothermics 2015, 55, 16–23. [Google Scholar] [CrossRef]
- Wight, N.M.; Bennett, N.S. Geothermal energy from abandoned oil and gas wells using water in combination with a closed wellbore. Appl. Therm. Energy 2015, 89, 908–915. [Google Scholar] [CrossRef]
- Mottaghy, D.; Dijkshoorn, L. Implementing an effective finite difference formulation for borehole heat exchangers into a heat and mass transport code. Renew. Energy 2012, 45, 59–71. [Google Scholar] [CrossRef]
- Macenić, M.; Kurevija, T. Revitalization of abandoned oil and gas wells for a geothermal heat exploitation by means of closed circulation: Case study of the deep dry well Pčelić-1. Interpretation 2018, 6, 1–9. [Google Scholar] [CrossRef]
- DiPippo, R. Second law assessment of binary generating power from low-temperature geothermal fluids. Geothermics 2004, 33, 565–586. [Google Scholar] [CrossRef]
- Kotas, T.J. The Exergy Method of Thermal Plant Analysis; Krieger Publishing Company: Malabar, FL, USA, 1995. [Google Scholar]
- Lee, K.C. Classification of geothermal resources by exergy. Geothermics 2001, 30, 431–442. [Google Scholar] [CrossRef]
- Barbacki, A. Classification of geothermal resources in Poland by exergy analysis—Comparative study. Renewable and Sustainable. Energy Rev. 2012, 16, 123–128. [Google Scholar]
- Ramajo, H.; Tritlla, J.; Levresse, G.; Tello-Hinojosa, E.; Ramírez, G.; Pérez, H. New SExI tools to evaluate the evolution and anthropic disturbance ingeothermal fields: The case of Los Azufres geothermal field, México. Rev. Mex. Cienc. Geol. 2010, 27, 520–529. [Google Scholar]
- Yari, M. Exergetic analysis of various types of geothermal power plants. Renew. Energy 2010, 35, 112–121. [Google Scholar] [CrossRef]
- Ganjehsarabi, H.; Gungor, A.; Dincer, I. Exergetic performance analysis of Dora II geothermal power plant in Turkey. Energy 2012, 46, 101–108. [Google Scholar] [CrossRef]
- Fallah, M.; Akbarpour Ghiasi, R.; Hasani Mokarram, N. A comprehensive comparison among different types of geothermal plants from exergy and thermoeconomic points of view. Therm. Sci. Eng. Prog. 2018, 5, 15–24. [Google Scholar] [CrossRef]
- Ozgener, L.; Hepbasli, A.; Dincer, I. Thermo-mechanical exergy analysis of Balcova geothermal district heating system in Izmir, Turkey. ASME J. Energy Resour. Technol. 2004, 126, 293–301. [Google Scholar] [CrossRef]
- Ozgener, L.; Hepbasli, A.; Dincer, I. Energy and exergy analysis of Salihli geothermal district heating system in Manisa, Turkey. Int. J. Energy Res. 2005, 29, 393–408. [Google Scholar] [CrossRef]
- Ozgener, L.; Hepbasli, A.; Dincer, I. Energy and exergy analysis of the Gonen geothermal district heating system, Turkey. Geothermics 2005, 34, 632–645. [Google Scholar] [CrossRef]
- Hepbasli, A. Thermodynamic analysis of a ground-source heat pump system for district heating. Int. J. Energy Res. 2005, 29, 671–687. [Google Scholar] [CrossRef]
- Kang, S.; Li, H.; Liu, L.; Lei, J.; Zhang, G. Exergy analysis of a novel CHP–GSHP coupling system. Appl. Therm. Eng. 2016, 93, 308–314. [Google Scholar] [CrossRef]
- Alimonti, C.; Conti, P.; Soldo, E. A comprehensive exergy evaluation of a deep borehole heat exchanger coupled with a ORC plant: The case study of Campi Flegrei. Energy 2019, 189, 116100. [Google Scholar]
- Casarosa, C.; Conti, P.; Franco, A.; Grassi, W.; Testi, D. Analysis of thermodynamic losses in ground source heat pumps and their influence on overall system performance. J. Phys. Conf. Ser. 2014, 547, 012006. [Google Scholar] [CrossRef]
- NIST. Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, version 9.1; National Institute of Standards and Technology, Standard Reference Data Program: Gaithersburg, MD, USA, 2013. [Google Scholar]
- Conti, P.; Testi, D.; Grassi, W. Revised heat transfer modeling of double-U vertical ground-coupled heat exchangers. Appl. Therm. Eng. 2016, 106, 1257–1267. [Google Scholar] [CrossRef]
- Conti, P. Dimensionless maps for the validity of analytical ground heat transfer models for GSHP applications. Energies 2016, 9, 890. [Google Scholar] [CrossRef]
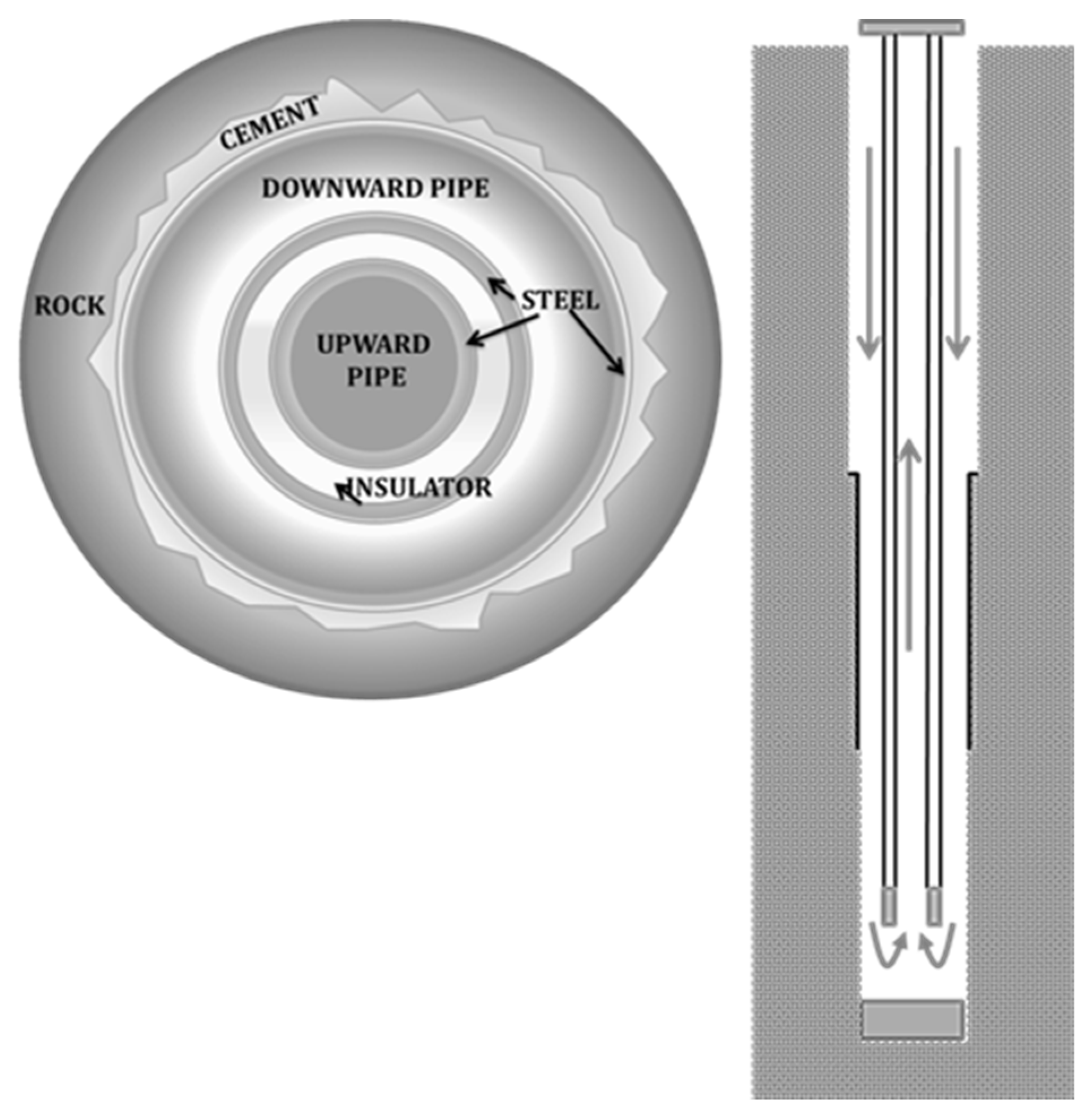
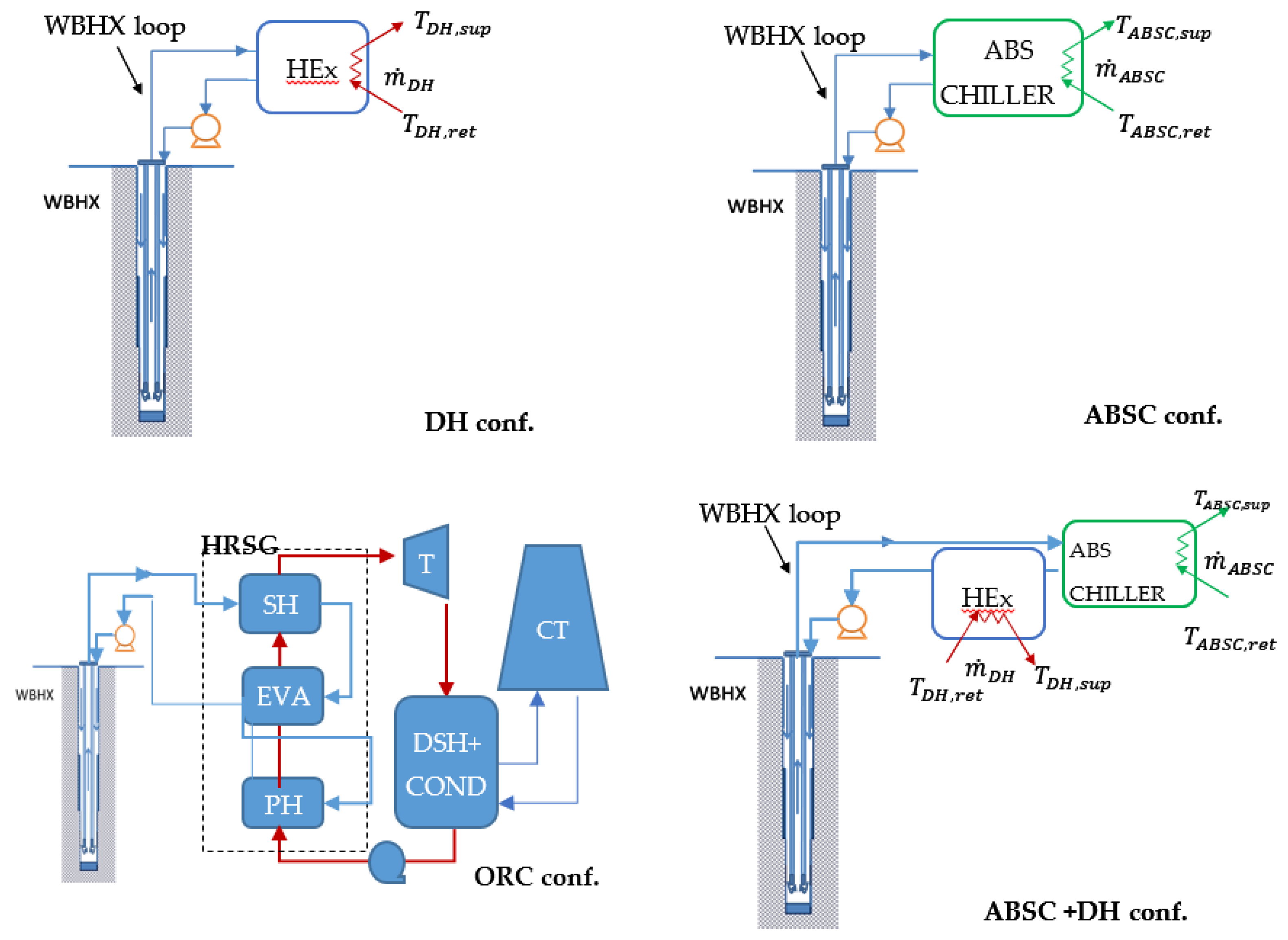

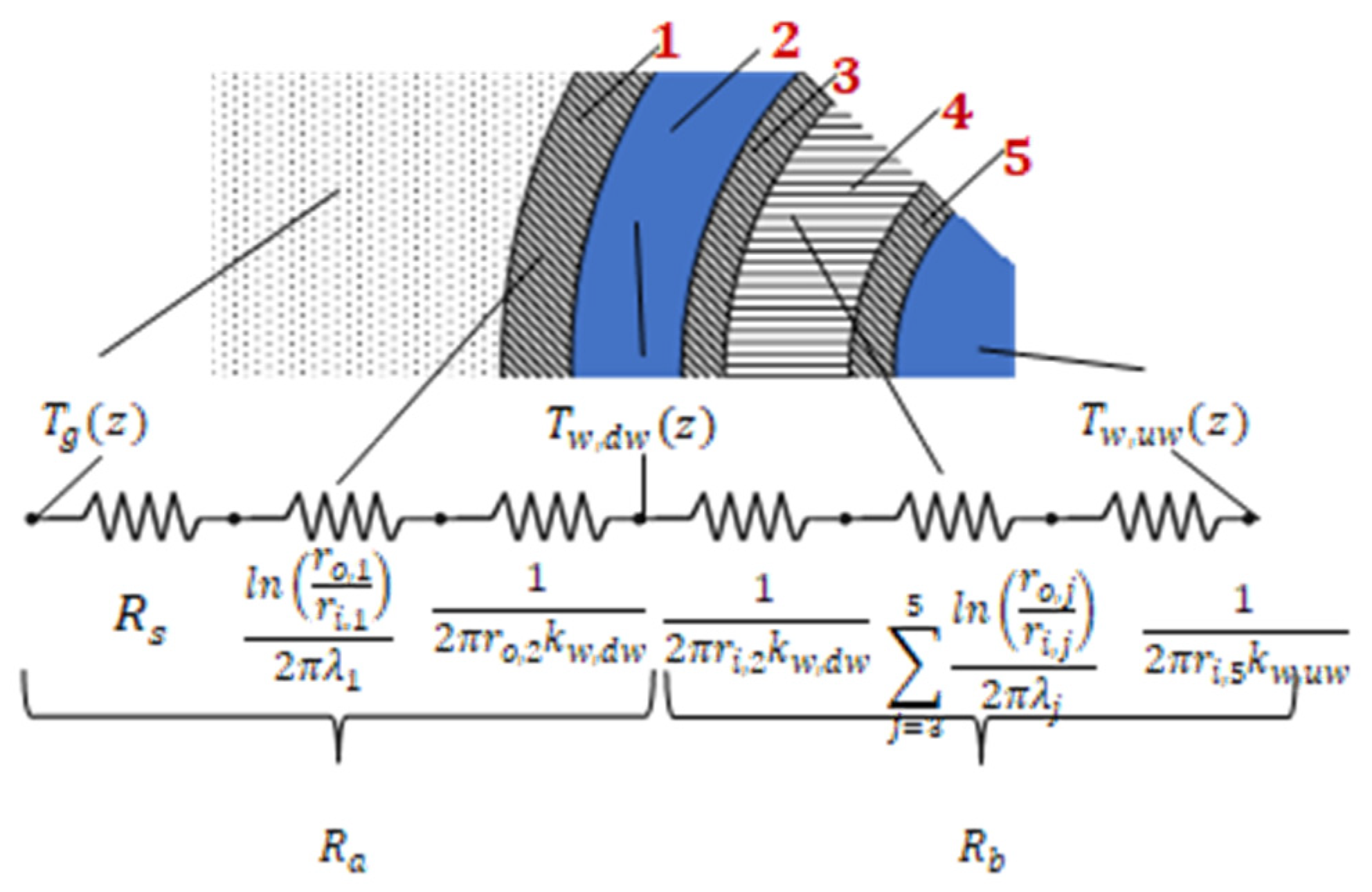
| Parameter | Value |
|---|---|
| Do/Di Layer 1 | 244.40/226.60 mm |
| Do/Di Layer 2 | 226.60/177.8 mm |
| Do/Di Layer 3 | 177.8/150.36 mm |
| Do/Di Layer 4 | 150.36/88.90 mm |
| Do/Di Layer 5 | 88.90/77.92 mm |
| Thermal conductivity steel (λ1, λ3, λ5) | 50 W/(mK) |
| Thermal conductivity insulation (λ4) | 0.04 W/(mK) |
| DH | ABSC | ORC | DH + ABSC | ORC + DH | |
|---|---|---|---|---|---|
| 0.43 | 0.10 | 0.21 | 0.33 | 0.24 | |
| 329 kW | - | - | 207 | 8 kW | |
| - | 184 kW | - | 140 kW | - | |
| - | - | 22 kW | - | 22 kW | |
| 47 kW | 10 kW | 22 kW | 37 kW | 24 kW | |
| 0.14 | 0.05 | 1 | 0.106 | 0.8 | |
| 5.4 m3/h | 5.4 m3/h | 5.4 m3/h | 5.4 m3/h | 5.4 m3/h | |
| 329 kW | 196 kW | 298 kW | 356 | 247 kW | |
| 73 °C | 100 °C | 80 °C | 68 °C | 90 °C | |
| 125 °C | 130 °C | 126 °C | 123 °C | 130 °C | |
| 109 kW | 92 kW | 105 kW | 113 kW | 99 kW | |
| 45 kW | 48 kW | 44 kW | 45 kW | 45 kW | |
| 18 kW | 35 kW | 39 kW | 31 kW | 29 kW |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alimonti, C.; Conti, P.; Soldo, E. Selecting the Optimal Use of the Geothermal Energy Produced with a Deep Borehole Heat Exchanger: Exergy Performance. Proceedings 2020, 58, 20. https://doi.org/10.3390/WEF-06912
Alimonti C, Conti P, Soldo E. Selecting the Optimal Use of the Geothermal Energy Produced with a Deep Borehole Heat Exchanger: Exergy Performance. Proceedings. 2020; 58(1):20. https://doi.org/10.3390/WEF-06912
Chicago/Turabian StyleAlimonti, Claudio, Paolo Conti, and Elena Soldo. 2020. "Selecting the Optimal Use of the Geothermal Energy Produced with a Deep Borehole Heat Exchanger: Exergy Performance" Proceedings 58, no. 1: 20. https://doi.org/10.3390/WEF-06912
APA StyleAlimonti, C., Conti, P., & Soldo, E. (2020). Selecting the Optimal Use of the Geothermal Energy Produced with a Deep Borehole Heat Exchanger: Exergy Performance. Proceedings, 58(1), 20. https://doi.org/10.3390/WEF-06912






