European and American Options Valuation by Unsupervised Learning with Artificial Neural Networks ^†

Abstract

Artificial neural networks (ANNs) have recently also been applied to solve partial differential equations (PDEs). In this work, the classical problem of pricing European and American financial options, based on the corresponding PDE formulations, is studied. Instead of using numerical techniques based on finite element or difference methods, we address the problem using ANNs in the context of unsupervised learning. As a result, the ANN learns the option values for all possible underlying stock values at future time points, based on the minimization of a suitable loss function. For the European option, we solve the linear Black–Scholes equation, whereas for the American option, we solve the linear complementarity problem formulation.

1. Introduction

The interest in machine learning techniques, due to the remarkable successes in different application areas, is growing exponentially. ANNs are learning systems based on a collection of artificial neurons that constitute a connected network. Such systems “learn” to perform tasks, generally without being programmed with task-specific rules. Many different financial problems have also been addressed with machine learning. The financial application on which we focus is the valuation of financial derivatives with PDEs. Generally, we can distinguish between supervised and unsupervised machine learning techniques. The goal of the current work is to solve the financial PDEs by applying unsupervised machine learning techniques. In such a case, only the inputs of the network are known, and based on a suitable loss function that needs to be minimized, the ANN should “converge” to the solution of the PDE problem. We will price European and American options modeled by the Black–Scholes PDE and look for solutions for all future time points and stock values. Thus, linear and nonlinear partial differential equations need to be solved.

2. Artificial Neural Networks Solving PDEs

We introduce the methodology following [1] to solve linear and nonlinear time-dependent PDEs by ANNs. Then, we write a general PDE problem as follows:

$$\begin{array}{cc}\hfill {\mathcal{N}}_I\left(v(t,x)\right)& =0,x\in \tilde{\Omega },t\in [0,T],\hfill \\ \hfill {\mathcal{N}}_B\left(v(t,x)\right)& =0\mathrm{on}\partial \tilde{\Omega },\hfill \\ \hfill {\mathcal{N}}_0\left(v(t^{*},x)\right)& =0x\in \tilde{\Omega }\mathrm{and}{t}^{*}=0\mathrm{or}{t}^{*}=T,\hfill \end{array}$$

(1)

where $v(t,x)$ denotes the solution of the PDE, ${\mathcal{N}}_I(·)$ is a linear or nonlinear time-dependent differential operator, ${\mathcal{N}}_B(·)$ is a boundary operator, ${\mathcal{N}}_0(·)$ is an initial or final time operator, $\tilde{\Omega }$ is a subset of ${\mathbb{R}}^D$, and $\partial \tilde{\Omega }$ denotes the boundary on the domain $\tilde{\Omega }$. The goal is to obtain $\widehat{v}(t,x)$ by minimizing a suitable loss function $L\left(v\right)$ over the space of k-times differentiable functions, where k depends on the order of the derivatives in the PDE, i.e.,

$$arg\underset{v\in {\mathcal{C}}^k}{\min }L\left(v\right)=\widehat{v}$$

where we denote by $\widehat{v}(t,x)$ the true solution of the PDE. A general expression for the loss function, defined in terms of the $L^p$ norm, including a weighting, is defined as follows [1,2]:

$$\begin{array}{cc}\hfill L\left(v\right)& =\lambda {\int }_{\Omega }\mid {\mathcal{N}}_I\left(v(t,x)\right){\mid }^{p}d\Omega +(1-\lambda ){\int }_{\partial \Omega }\left(\mid {\mathcal{N}}_B\left(v(t,x)\right){\mid }^p+\mid {\mathcal{N}}_0\left(v(t,x)\right){\mid }^p\right)d\gamma ,\hfill \end{array}$$

(2)

where $\Omega =\tilde{\Omega }\times [0,T]$ and $\partial \Omega$ the boundary of $\Omega$. Financial options with early-exercise features give rise to free boundary PDE problems. We will focus on the reformulation of the free boundary problem as a LCP. The generic LCP formulation reads:

$$\begin{array}{cc}\hfill \max ({\mathcal{N}}_0\left(v(t,x)\right),{\mathcal{N}}_I\left(v(t,x)\right))& =0,x\in \tilde{\Omega },t\in [0,T],\hfill \\ \hfill {\mathcal{N}}_B\left(v(t,x)\right)& =0,\mathrm{on}\partial \tilde{\Omega },\hfill \\ \hfill {\mathcal{N}}_0\left(v(t^{*},x)\right)& =0,x\in \tilde{\Omega }\mathrm{and}{t}^{*}=0\mathrm{or}{t}^{*}=T.\hfill \end{array}$$

Our expression for the loss function, to solve the linear complementarity problem, is as follows:

$$\begin{array}{cc}\hfill L\left(v\right)& =\lambda {\int }_{\Omega }\mid \max ({\mathcal{N}}_0(t,x,v),{\mathcal{N}}_I(t,x,v)){\mid }^{p}d\Omega +(1-\lambda ){\int }_{\partial \Omega }\left(\mid {\mathcal{N}}_B(t,x,v){\mid }^p+\mid {\mathcal{N}}_0(t,x,v){\mid }^p\right)d\gamma .\hfill \end{array}$$

(3)

3. Financial Derivatives Pricing PDEs

In this section, the option pricing partial differential equation problems are presented. We briefly introduce the European asset model, the American and multi-asset options model being easily extended.

The underlying asset $S_t$ is assumed to pay a constant dividend yield $\delta$, and follows the geometric Brownian motion:

$$d{S}_t=(\mu -\delta )S_{t}dt+\sigma S_{t}d{W}_t^P$$

(4)

where $W_t^P$ is a Brownian motion. Assuming there are no arbitrage opportunities, the European option value follows from the Black–Scholes equation:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\mathcal{L}\left(v\right)={\partial }_{t}v+\mathcal{A}v-rv=0S\in \tilde{\Omega }t\in [0,T)\hfill \\ v(T,S)=H\left(S\right)\hfill \end{array}\right.\end{array}$$

(5)

where operator $\mathcal{A}$ is the classical Black–Scholes operator, and function H denotes the option’s payoff. Then, the loss function is defined as:

$$\begin{array}{cc}\hfill L\left(v\right)& =\lambda {\int }_{\Omega }\mid \mathcal{L}\left(v(t,x)\right){\mid }^{p}d\Omega \hfill \\ \hfill & +(1-\lambda ){\int }_{\partial \Omega }\left(\mid v(t,x)-G(t,x){\mid }^p+\mid v(t,x)-H\left(x\right){\mid }^p\right)d\gamma ,\hfill \end{array}$$

(6)

where functions G and H denote the values of the spatial boundary conditions and final condition, respectively. The integral terms in the loss function are approximated by Monte Carlo techniques.

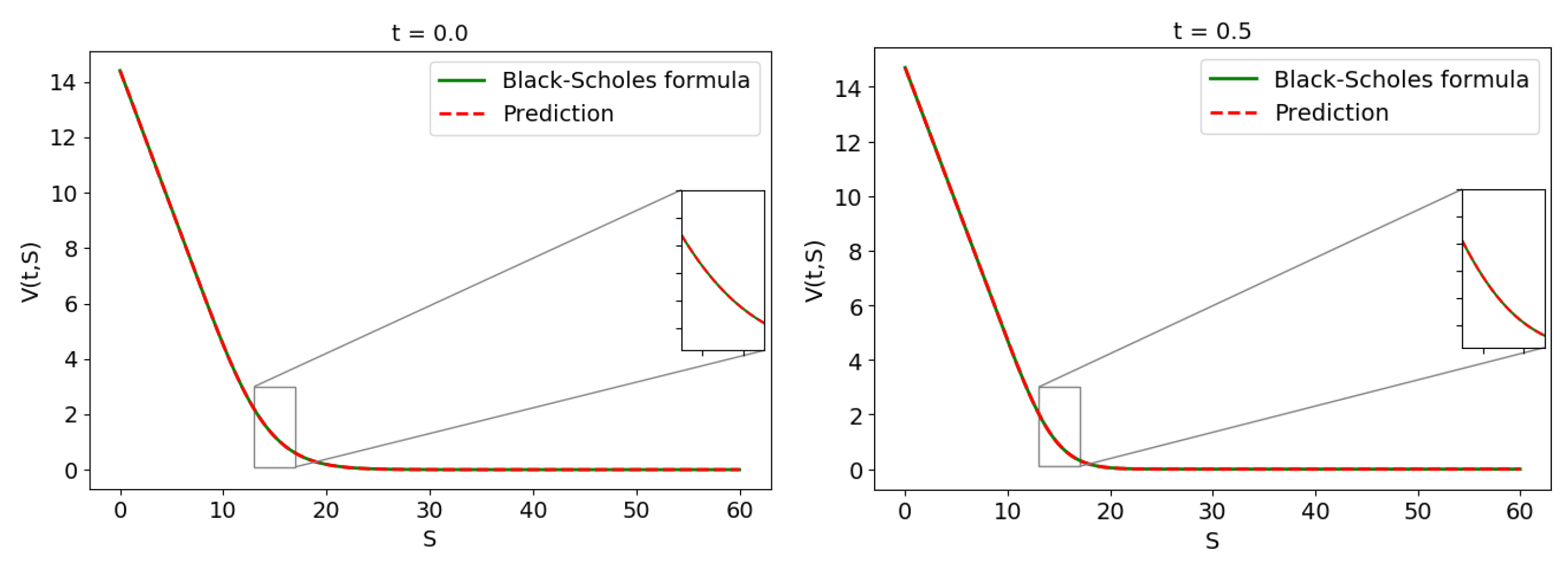
4. ANN Option Pricing Results

We start with a European put option, with the following parameters’ values: $\sigma =0.25$, $r=0.04$, $T=1$, $K=15$, $S_{\infty }=4K$, $\delta =0.0$. In Figure 1, the ANN-based, trained, and the analytical solution are plotted for two time instances. The relative error, with $\lambda =0.5$, is equal to 2.23 × 10⁻⁴.

Finally, in order to show the accuracy of the method applied to train the ANN to price American options depending on two asset prices, the relative error is presented in

Table 1. Error for different multi-asset American options.

	Error
Max-call	$1.73\times {10}^{-3}$
Spread	$2.45\times {10}^{-3}$
Arithmetic average put	$6.42\times {10}^{-3}$

.