Numerical Simulation of a Nonlinear Problem Arising in Heat Transfer and Magnetostatics ^†

Abstract

We present a numerical model that comprises a nonlinear partial differential equation. We apply an adaptive stabilised mixed finite element method based on an a posteriori error indicator derived for this particular problem. We describe the numerical algorithm and some numerical results.

1. Introduction

We consider the mathematical model from [1]. The model comprises a second order nonlinear elliptic partial differential equation over a bounded domain $\mathsf{\Omega }$ in ${\mathbb{R}}^2$, provided with Dirichlet boundary conditions over the contour $\mathsf{\Gamma }$:

$$\left\{\begin{array}{ccc}\hfill -\nabla ·\left(k\right(·,|\nabla u|)\nabla u)& =& f\mathrm{in}\mathsf{\Omega },\hfill \\ \hfill u& =& g\mathrm{on}\mathsf{\Gamma }.\hfill \end{array}\right.$$

(1)

The unknown u can be temperature, magnetic potential, etc., $|·|$ denotes the Euclidean norm and ∇ and $\nabla ·$ denote, respectively, the usual gradient and divergence operators. The functions k, f and g are data, and we assume that $k:\mathsf{\Omega }\times [0,+\infty )\to \mathbb{R}$ satisfies the following bound, for two positive constants $k_1$ and $k_2$: $k_1\le k(\mathbf{x},s)+s\frac{\partial }{\partial s}k(\mathbf{x},s)\le k_2,\forall (\mathbf{x},s)\in \mathsf{\Omega }\times [0,+\infty )$.

Problem (1) allows to predict a wide range of physical phenomena, such as magnetostatics and heat transfer. Due to the nonlinearity, we need to resort to numerical methods. We apply an adaptive stabilized mixed finite element method and present some results from our numerical experiments.

2. Adaptive Augmented Mixed Finite Element Method

We introduce two additional unknowns, $\mathbf{t}=\nabla u$ and $\sigma =k(·,|\mathbf{t}\left|\right)\mathbf{t}$, and define the function space $X:={\left[L^2\left(\mathsf{\Omega }\right)\right]}^2\times H(\nabla ·,\mathsf{\Omega })\times L^2\left(\mathsf{\Omega }\right)$, where $L^2\left(\mathsf{\Omega }\right)$ is the space of square integrable functions and $H(\nabla ·,\mathsf{\Omega }):=\{\mathbf{v}\in {\left[L^2\left(\mathsf{\Omega }\right)\right]}^2;\nabla ·\mathbf{v}\in L^2\left(\mathsf{\Omega }\right)\}$. In order to approximate the triplet $(\mathbf{t},\sigma ,u)$, the domain is divided into triangular cells that conform a mesh (see Figure 1a). In each of those cells an approximation of the unknowns is calculated. The corresponding function space is $X_h:={\mathcal{P}}_0\times {\mathcal{RT}}_0\times {\mathcal{P}}_1$, with ${\mathcal{P}}_k$ being the space of polynomials of degree $\le k$ and ${\mathcal{RT}}_0$ is the lowest order Raviart Thomas space. We consider the following discrete problem: find $({\mathbf{t}}_h,{\sigma }_h,u_h)\in X_h$ such that

$$A(({\mathbf{t}}_h,{\sigma }_h,u_h),({\mathbf{s}}_h,{\tau }_h,v_h))=F({\mathbf{s}}_h,{\tau }_h,v_h),\forall ({\mathbf{s}}_h,{\tau }_h,v_h)\in X_h$$

(2)

where

$$\begin{array}{c}{\displaystyle A((\mathbf{t},\sigma ,u),(\mathbf{s},\tau ,v)):={\int }_{\mathsf{\Omega }}k(·,|\mathbf{t}\left|\right)\mathbf{t}·\mathbf{s}-{\int }_{\mathsf{\Omega }}\sigma ·\mathbf{s}+{\int }_{\mathsf{\Omega }}\tau ·\mathbf{t}+{\int }_{\mathsf{\Omega }}u\nabla ·\tau -{\int }_{\mathsf{\Omega }}v\nabla ·\sigma +}\hfill \\ {\displaystyle {\kappa }_1{\int }_{\mathsf{\Omega }}(\sigma -k(·,\left|\mathbf{t}\right|\left)\mathbf{t}\right)·\tau +{\kappa }_2{\int }_{\mathsf{\Omega }}\nabla ·\sigma \nabla ·\tau +{\kappa }_3{\int }_{\mathsf{\Omega }}(\nabla u-\mathbf{t})·(\nabla v+\mathbf{s})+{\kappa }_4{\int }_{\mathsf{\Gamma }}uv}\hfill \end{array}$$

(3)

$$F(\mathbf{s},\tau ,v):={\int }_{\mathsf{\Gamma }}\tau ·\mathbf{n}g+{\int }_{\mathsf{\Omega }}fv-{\kappa }_2{\int }_{\mathsf{\Omega }}f\nabla ·\tau +{\kappa }_4{\int }_{\mathsf{\Gamma }}gv$$

(4)

with ${\kappa }_i$ being positive constants. The nonlinear form $A(·,·)$ is strongly monotone, Lipschitz-continuous and bounded for appropriate values of the parameters ${\kappa }_i$ so that problem (2) has a unique solution.

We consider an adaptive algorithm, which estimates the local error in each cell, and refines the mesh over those regions with the highest error. On each triangle, we introduce the following novel error indicator, which is reliable and locally efficient [2]:

$$\begin{array}{ccc}\hfill {\theta }_T^2& :=& {\displaystyle \parallel \nabla u_h-{\mathbf{t}}_h{\parallel }_{{\left[L^2\left(T\right)\right]}^2}^2+\parallel f+\nabla ·{\sigma }_h{\parallel }_{L^2\left(T\right)}^2+\parallel {\sigma }_h-k(·,|{\mathbf{t}}_h\left|\right){\mathbf{t}}_h{\parallel }_{{\left[L^2\left(T\right)\right]}^2}^2}\hfill \\ \hfill & +& {\displaystyle \sum _{e\in E\left(T\right)\cap E\left(\mathsf{\Gamma }\right)}{h}_e(\parallel g-u_h{\parallel }_{L^2\left(e\right)}^2+\parallel \frac{d}{ds}(g-u_h){\parallel }_{L^2\left(e\right)}^2)}\hfill \end{array}$$

(5)

where $E\left(T\right)$ denotes the set of edges of T and $E\left(\mathsf{\Gamma }\right)$ the set of edges in the boundary.

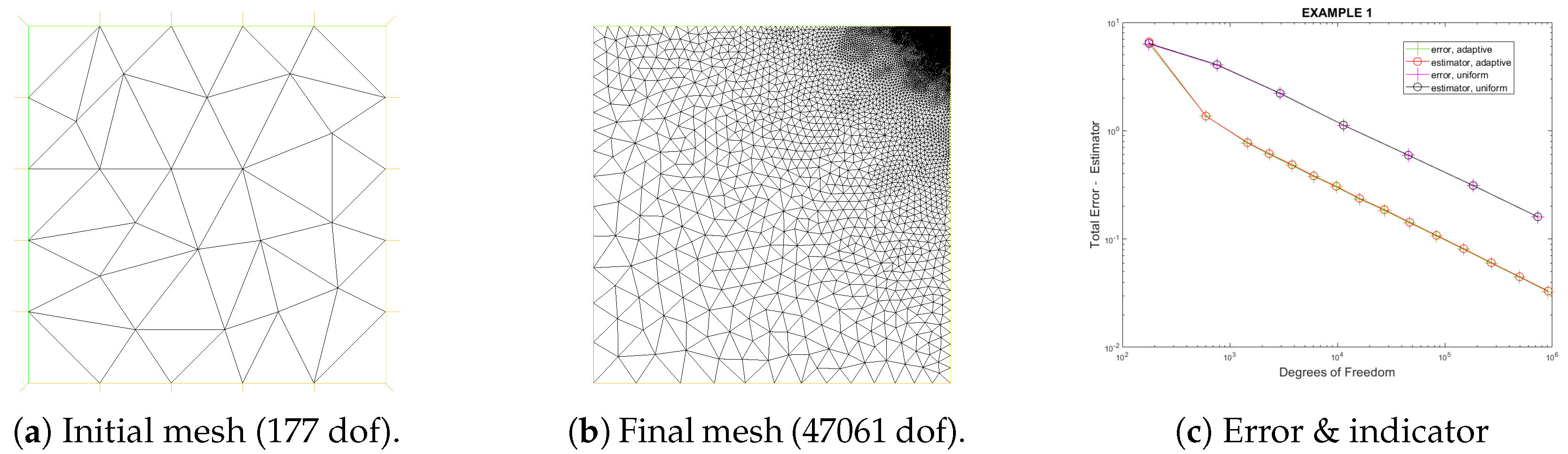
3. Results and Discussion

The adaptive algorithm was tested on a singular example over the unit square with a singularity in its upper right corner. The exact solution is $u(x,y)={(2.1-x-y)}^{-1/3}$. In Figure 1b, we can see that the algorithm refines the mesh near the singularity. Figure 1c shows a graph that compares, for both uniform and adaptive refinements, the exact error and the defined indicator vs. degrees of freedom (dof). With the adaptive algorithm the total error is lower, and a good agreement between error and indicator is seen. In fact, the efficiency index, which is the quotient between indicator and total error, tends to one as the mesh size decreases.

These simulations were carried out in FreeFEM++, following the mesh refinement algorithm proposed in [3], and the nonlinear system was solved with Newton’s method with a tolerance of ${10}^{-9}$, needing four iterations.