Multi-Technology Correction Based 3D Human Pose Estimation for Jump Analysis in Figure Skating ^†

Abstract

Jump analysis in figure skating is important. Recovering the 3D pose of a figure skater has become increasingly important. However, issues such as restrictions from an athlete’s clothing, self-occlusion, abnormal pose and so on will result in poor results. This paper proposes a multi-technology correction framework to obtain a 3D human pose. The framework consists of three key components: temporal information-based mutational point correction, multi-perspective-based reconstructed point selection and trajectory smoothness-based inaccurate point correction. Firstly, temporal information is used to correct the mutational points at the 2D level. Secondly, a multi-perspective is used to select the correct spatial points at the 3D level. Thirdly, trajectory smoothness is used to correct inaccuracies at the 3D level. This work will serve the purpose of displaying the 3D animated pose of a figure skater. The quality grade of the result rate on the test sequences is 87.25%.

1. Introduction

Recently, estimating 3D human poses in sports has attracted academic interests for its vast potential. Analyzing the 3D jump pose in figure skating is an active research area, as it plays a significant role for a figure skater’s behavior understanding. It can not only objectively evaluate the performance of a figure skater’s jump, but also enhance the audience’s entertainment experience by displaying the jump height, spatial trajectory, action details and other information obtained from a figure skating video. Unfortunately, the diverse variations in background, costume, abnormal pose, self-occlusion, illumination and camera parameters make it a challenging problem. Recent advanced technologies in estimating 3D pose have not covered these variations appropriately. Motivated by these problems, this work has developed a transformation system to generate a 3D pose conditioned on the corresponding 2D pose.

The current related work cannot meet the requirements for estimating the 3D pose of figure skaters. It is well known that the goal of 3D human pose estimation is to localize key points of single or multiple human bodies in a 3D space. However, most of the previous 3D human pose estimation methods utilize a convolutional neural network and performed well on large-scale publicly datasets [1,2,3,4]. However, many methods estimate the relative 3D pose to a reference point in the body. Then, according to the prior information such as the length of the bone, to calculate the final 3D pose is done by adding the 3D coordinates of the reference point to the estimated relative coordinates [5,6]. The 3D coordinates obtained by these methods are not the real positions of key points in the space. This is not a suitable method for the analysis of jumps in figure skating because it lacks a 3D annotated dataset. Currently, a 3D dataset is much more difficult to obtain because accurate 3D pose annotation requires using motion capture in indoor artificial settings. However, these are not possible for figure skating which requires a large venue.

Different from the previous 3D pose estimation method, this work obtains the athlete’s 3D pose with fully spatial realism by considering the particularity of figure skating as shown in Figure 1. The whole system takes as the input a sequence of images capturing the motion of a figure skater from a synchronized multi-perspective and outputs the 3D joints of the target person in the form of a 3D human model video. The three proposed methods are as follows: temporal information-based mutational point correction, multi-perspective-based reconstructed point selection and trajectory smoothness-based inaccurate point correction. The details of the proposals will be introduced in Section 3.

The rest of this paper is organized as follows. The whole system is introduced in Section 2. Details of the proposed methods are explained in Section 3. Finally, the experiment and conclusion are in Section 4 and Section 5, respectively.

2. Framework

2.1. 2D Pose Estimation

The work first obtains the 2D pixel values of the human joints through the multi-person 2D pose estimation method OpenPose [7] as shown in Figure 2. This approach uses a nonparametric representation, which is referred to as part affinity fields (PAFs), to associate body parts with individuals in the image. The architecture encodes the global context, allowing a greedy bottom-up parsing step to achieve a real-time performance. The architecture is designed to jointly learn part locations and their association.

2.2. Camera Calibration and Binocular Stereo Reconstruction

In order to determine the relationship between the 3D geometric position of the figure skater’s joint spatial point and its corresponding 2D point in the image, it is necessary to establish a geometric model of camera imaging. These geometric model parameters are camera parameters, and the process of solving the parameters is called camera calibration. The accuracy of the calibration result and the stability of the algorithm directly affect the quality of the results. The solution process of the camera calibration matrix is as follows: z is an unknown scale factor which corresponds to the depth; u and v are the pixel coordinate values; X, Y and Z are the spatial coordinate values; and$M_{3X4}$ is the camera calibration matrix.

$$\mathrm{z}\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=M_{3X4}\left[\begin{array}{c}\begin{array}{c}X\\ Y\end{array}\\ \begin{array}{c}Z\\ 1\end{array}\end{array}\right]$$

(1)

Binocular stereo vision mimics human eyes to obtain 3D information and consists of two cameras. The two cameras form a triangular relationship with the measured object in space. As shown in Figure 3b, the spatial coordinate can be obtained according to the calibration matrix and the human joints’ pixel value of the two camera planes.

2.3. Dataset

As shown in Figure 3a, which is a standard figure skating venue, with six cameras placed every 60 degrees within the auditorium, the visual fields of these cameras cover the red area simultaneously. The resolution of sequences is 1920 times 1080, and the frame rate is 60 frames per second (fps). Synchronized images which contain the target from six perspectives are available at any moment.

3. Proposed Methods

3.1. Mutational Point Correction

Due to the particularity of figure skating, such as the restrictions of figure skater’s clothing, the self- occlusion, abnormal pose, large venues and other factors, accurate 2D detection results cannot be obtained even after an advanced 2D human pose estimation method [7]. Proposal 1 will mainly solve the problems at the 2D level as shown in Figure 4. The errors in 2D information can be roughly divided into three types of mutations: the left and right are reversed, the wrong identification and the sudden appearance and disappearance of the joints.

Except for the key points in the face and neck, all the key points have left and right sides. All three kinds of mutation points are first judged with the threshold value of the previous frame. Here, the threshold is defined as a circle with the key point of the previous frame as the center and a certain pixel value as the radius. If the threshold is exceeded, the values of the left and right sides will be exchanged. Thus, the mutation caused by a left–right inversion can be corrected. Then, perform the second threshold judgment where wrong identification can be detected. As shown in Figure 5b, the identification of these errors can be judged as a very serious error, which is difficult to correct. If an inappropriate correction method is used, it will lead to error superposition and introduce a larger error, so discard the serious error. Due to the figure skater’s self-occlusion, the key points will appear and disappear suddenly, which is difficult to correct at the 2D level, so correct it at the 3D level.

3.2. Reconstructed Point Selection

Six cameras are used to capture the dataset. In theory, according to the stereo binocular reconstruction principle, $C_6^2$ spatial points will be reconstructed because the principle of reconstruction requires a clear triangular relationship between two different cameras. Therefore, it is necessary to discard the camera combinations which cannot form a distinct triangle with the target athlete such as 0-1, 2-5 and 3-4. For reconstructed points which can be used, if any two are not equal, the weighted average will be calculated. Otherwise, use majority rules to get the accurate one. The weighted average (w) is calculated as follows: S is the reconstruction point, $\eta$ is the weight of S and the value of $\eta$ is determined according to the relative displacement from the previous frame.

$${\mathrm{w}=\mathsf{\eta }}_1{S}_1{+\mathsf{\eta }}_2{S}_2+\cdots {+\mathsf{\eta }}_{\mathrm{n}}{S}_n$$

(2)

$$\mathsf{\eta }=\frac{30}{\sqrt{{\left({\mathrm{x}}_{\mathrm{t}}{-\mathrm{x}}_{\mathrm{t}-1}\right)}^2+{\left({\mathrm{y}}_{\mathrm{t}}{-\mathrm{y}}_{\mathrm{t}-1}\right)}^2+{\left({\mathrm{z}}_{\mathrm{t}}{-\mathrm{z}}_{\mathrm{t}-1}\right)}^2}}$$

(3)

3.3. Inaccurate Point Correction

In order to correct inaccurate reconstructed points, it is necessary to utilize the smoothness of the spatial trajectory. Figure 6a shows the spatial trajectory of the skater’s left elbow. As shown in Figure 6b, the red dot is the key point of the first two frames, and the gray is the current reconstructed point. A straight line can be determined according to the key points of the previous two frames. If the reconstructed point of the current frame is far away from this line, the position of the current frame’s key point needs to be predicted on the line.

4. Experiment

The experiment is run on the test videos which contain 51 groups of jumps in total. The test videos are six corner perspectives of the figure skating venue. The test dataset contains 23 groups of 1 turn jump, 10 groups of 2 turn jumps, 15 groups of 3 turn jumps and 3 groups of a falling jump. For the software environment, the proposed method is implemented on C++ and OpenCV 3.4.1.

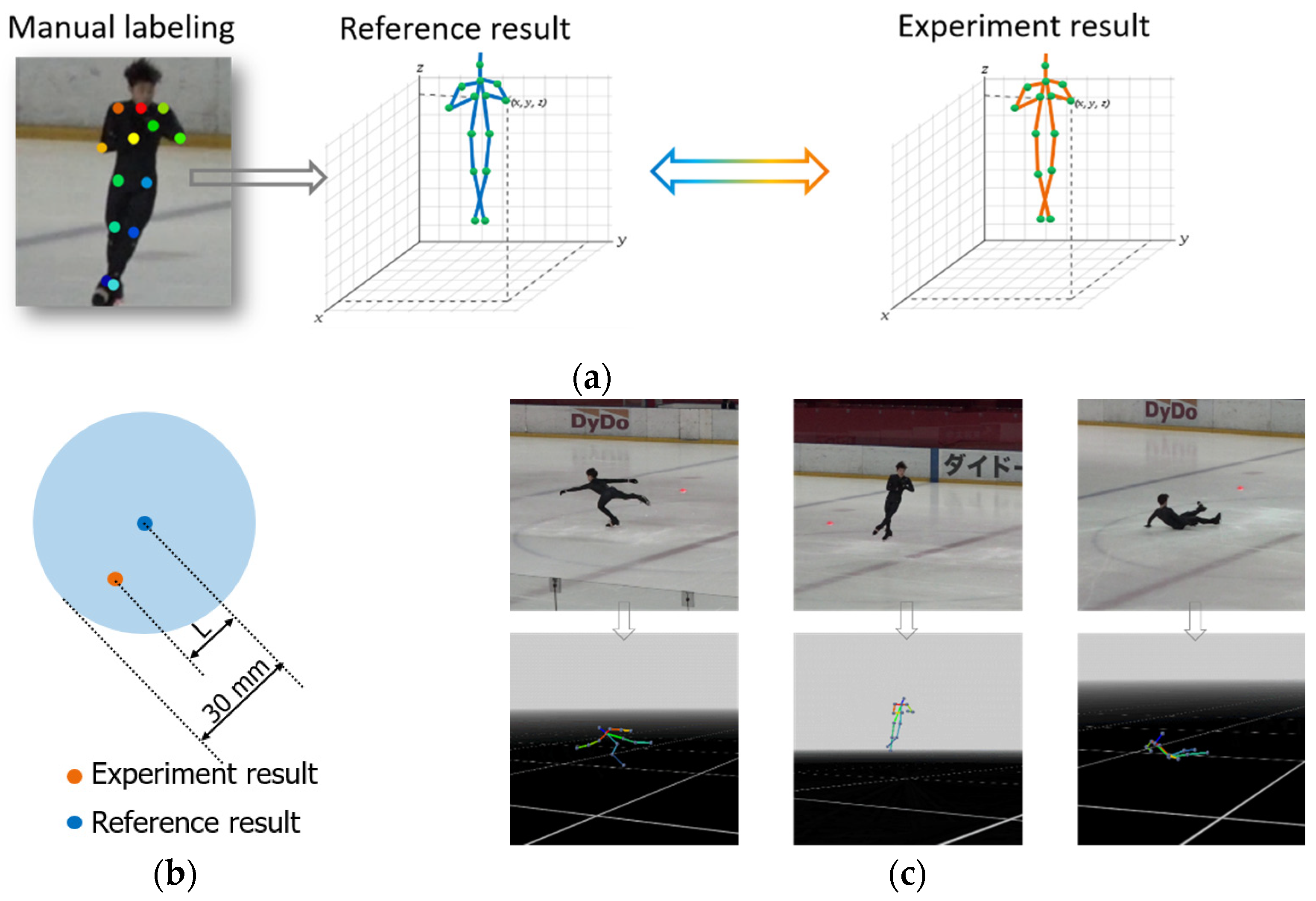
The definition of a successful frame is that if comparing the experimental results with the reference results, the 14 joint points coincide within a certain error range, then it is considered a successful frame, as shown in Figure 7a. The allowable range of error is defined by the fact that the experimental results do not exceed the sphere with a radius of 30 mm centered on the reference point, as shown in Figure 7b.

Figure 7. The quality grade of results is determined by comparing them with the reference spatial points which are reconstructed from the manually labeled 2D pixel values. (a) Evaluation method; (b) the allowable range of error; (c) experimental result. The quality grade of results is defined as

Figure 7. The quality grade of results is determined by comparing them with the reference spatial points which are reconstructed from the manually labeled 2D pixel values. (a) Evaluation method; (b) the allowable range of error; (c) experimental result. The quality grade of results is defined as

$$\mathrm{quality}\mathrm{grade}=\frac{\mathrm{successful}\mathrm{frames}}{\mathrm{total}\mathrm{frames}}$$

(4)

5. Conclusions

This work has developed a system to obtain the 3D jump pose of a figure skater. At the core of the approach, this method corrects inaccurate or even erroneous reconstruction results by combining spatial-temporal information and a multi-perspective during the process of 2D-to-3D pose transformation. The proposed system outperforms previous 3D pose estimation in terms of spatial the coordinates’ authenticity. The quality grade of the experimental result is 87.25%, based on the test sequences which have different types of jumps in figure skating. For future work, we plan to change the network of pose estimation as needed, adding key points such as hands and feet, at the same time as improving the algorithm to realize real-time. After these modifications, the system can be applied to the objective performance evaluation of figure skaters and the real-time display of figure skating TV broadcasts to enhance the audience entertainment experience.