Analysis of Swimming Motion for a Swimmer with Unilateral Transradial Deficiency to Develop Better Training Paddles †
Abstract
1. Introduction
2. Methods
2.1. Experiment
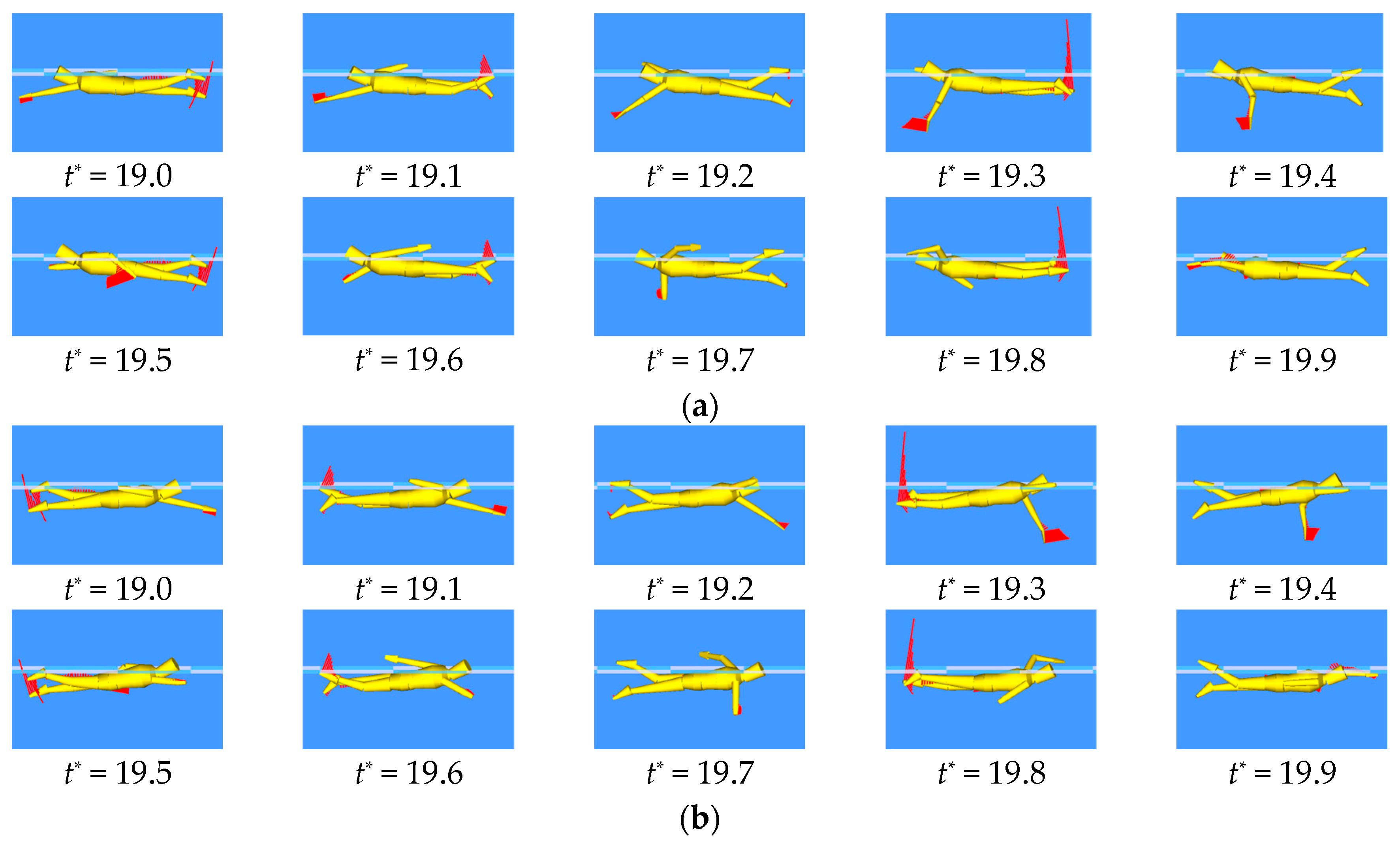
2.2. Simulation
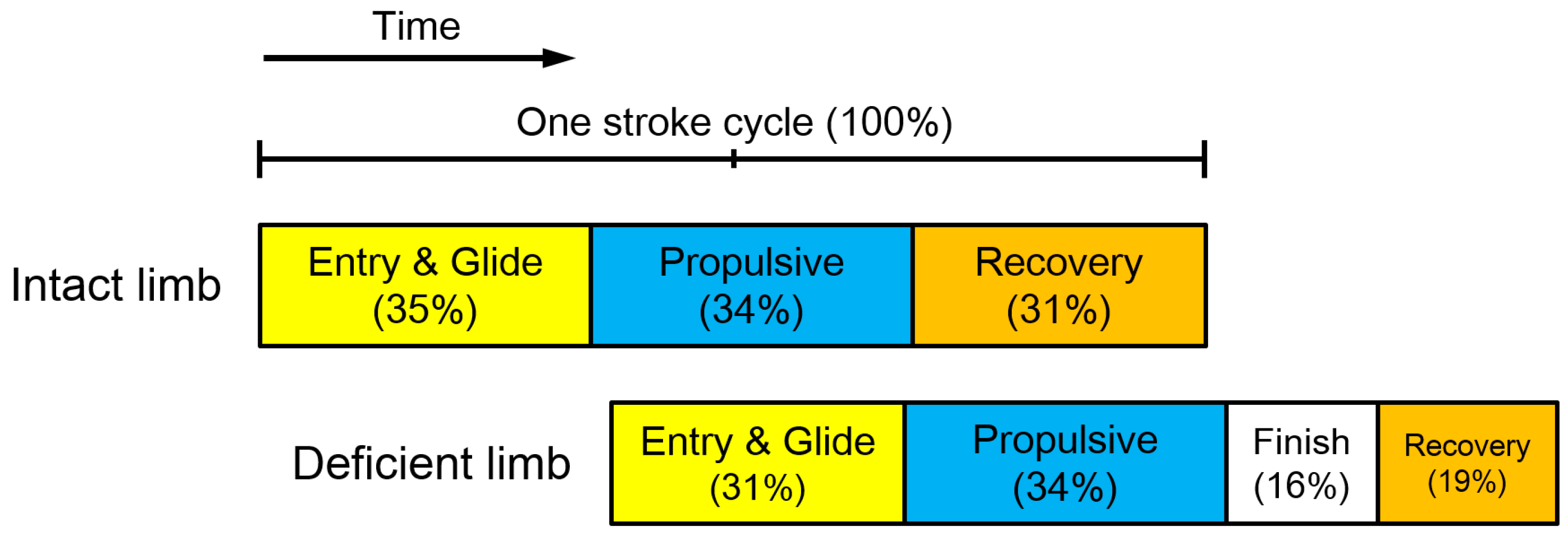
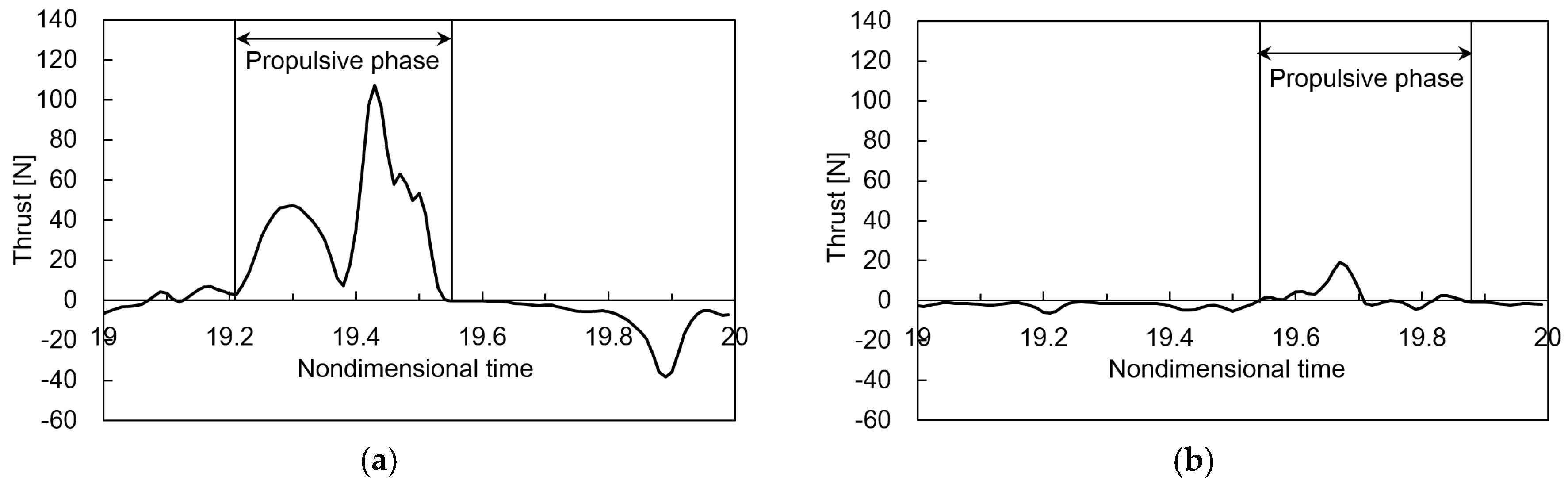
3. Results and Discussion
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Nakashima, M.; Favreau, A.; Terada, M. Design and development of a paddle for a swimmer with trans-radial amputation. In Proceedings of the 17th International Symposium on Computer Simulation in Biomechanics, Canmore, AB, Canada, 28–30th July 2019; pp. 79–80. [Google Scholar]
- Osborough, C.; Payton, C.; Daly, D. Relationships between the front crawl stroke parameters of competitive unilateral arm amputee swimmers, with selected anthropometric characteristics. J. Appl. Biomech. 2009, 25, 304–312. [Google Scholar] [CrossRef] [PubMed]
- Osborough, C.; Payton, C.; Daly, D. Influence of swimming speed on inter-arm coordination in competitive unilateral arm amputee front crawl swimmers. Hum. Mov. Sci. 2010, 29, 921–931. [Google Scholar] [CrossRef]
- Osborough, C.; Payton, C.; Daly, D. Effect of swim speed on leg-to-arm coordination in unilateral arm amputee front crawl swimmers. J. Sports Sci. 2015, 33, 1523–1531. [Google Scholar] [CrossRef] [PubMed]
- Figueiredo, P.; Willing, R.; Alves, F.; Vilas-Boas, J. Biophysical characterization of a swimmer with a unilateral arm amputation: A case study. Int. J. Sports Physiol. Perform. 2014, 9, 1050–1053. [Google Scholar] [CrossRef] [PubMed]
- Lecrivain, G.; Slaouti, A.; Payton, C.; Kennedy, I. Using reverse engineering and computational fluid dynamics to investigate a lower arm amputee swimmer’s performance. J. Biomech. 2008, 41, 2855–2859. [Google Scholar] [PubMed]
- Lecrivain, G.; Payton, C.; Slaouti, A.; Kennedy, I. Effect of body roll amplitude and arm rotation speed on propulsion of arm amputee swimmers. J. Biomech. 2010, 43, 1111–1117. [Google Scholar] [CrossRef] [PubMed]
- Nakashima, M.; Miura, Y.; Satou, K. Development of swimming human simulation model considering rigid body dynamics and unsteady fluid force for whole body. J. Fluid Sci. Tech. 2007, 2, 56–67. [Google Scholar] [CrossRef]
- Swimming Human Simulation Software “Swumsuit”. Available online: http://www.swum.org/swumsuit/ (accessed on 9 November 2019).
- Nakashima, M. Mechanical study of standard six beat front crawl swimming by using swimming human simulation model. J. Fluid Sci. Tech. 2007, 2, 290–301. [Google Scholar] [CrossRef]
- Nakashima, M.; Maeda, S.; Miwa, T.; Ichikawa, H. Optimizing simulation of the arm stroke in crawl swimming considering muscle strength characteristics of athlete swimmers. J. Biomech. Sci. Eng. 2012, 7, 102–117. [Google Scholar] [CrossRef][Green Version]
- Nakashima, M.; Ono, A. Maximum joint torque dependency of the crawl swimming with optimized arm stroke. J. Biomech. Sci. Eng. 2014, 9, 1–9. [Google Scholar] [CrossRef][Green Version]
- Nakashima, M.; Nemoto, C.; Kishimoto, T.; Terada, M.; Ikuta, Y. Optimizing simulation of arm stroke in freestyle for swimmers with hemiplegia. Mech. Eng. J. 2018, 5, 17–00377. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakashima, M.; Tebbe, J. Analysis of Swimming Motion for a Swimmer with Unilateral Transradial Deficiency to Develop Better Training Paddles. Proceedings 2020, 49, 9. https://doi.org/10.3390/proceedings2020049009
Nakashima M, Tebbe J. Analysis of Swimming Motion for a Swimmer with Unilateral Transradial Deficiency to Develop Better Training Paddles. Proceedings. 2020; 49(1):9. https://doi.org/10.3390/proceedings2020049009
Chicago/Turabian StyleNakashima, Motomu, and Jacob Tebbe. 2020. "Analysis of Swimming Motion for a Swimmer with Unilateral Transradial Deficiency to Develop Better Training Paddles" Proceedings 49, no. 1: 9. https://doi.org/10.3390/proceedings2020049009
APA StyleNakashima, M., & Tebbe, J. (2020). Analysis of Swimming Motion for a Swimmer with Unilateral Transradial Deficiency to Develop Better Training Paddles. Proceedings, 49(1), 9. https://doi.org/10.3390/proceedings2020049009



