A Study on the Mechanical Characteristics of String Planes of Badminton Racquets by Nonlinear Finite Element Analysis †
Abstract
:1. Introduction
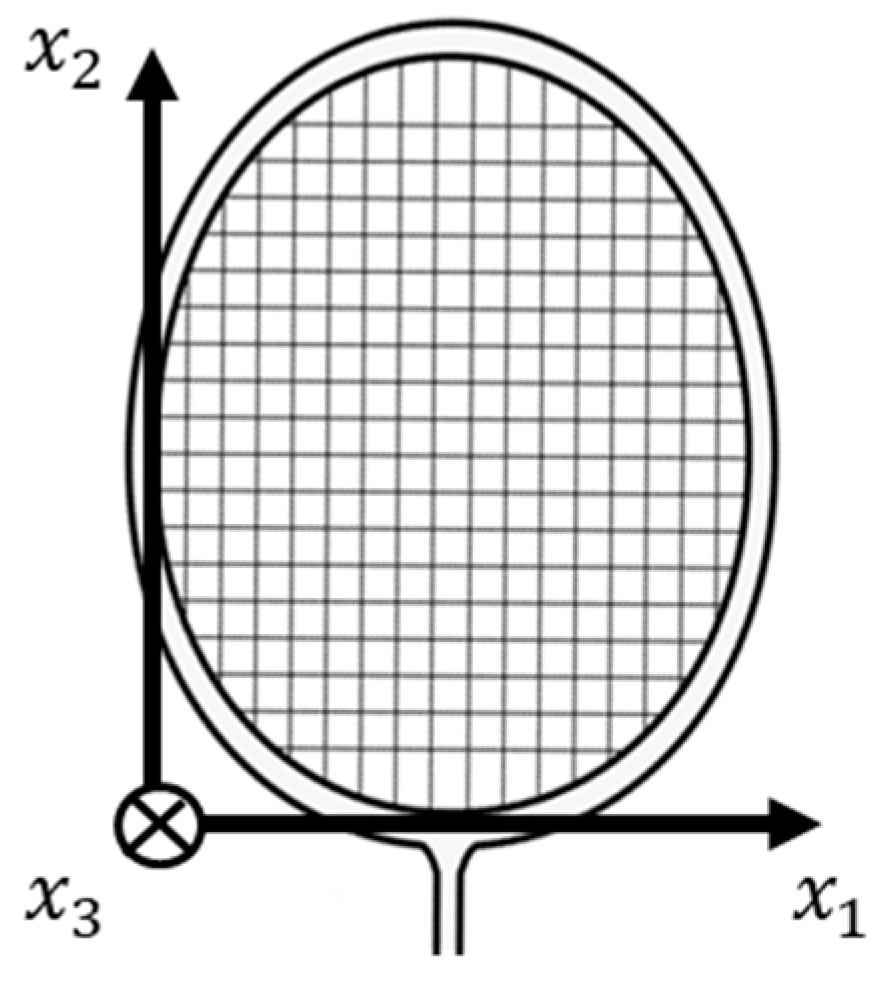
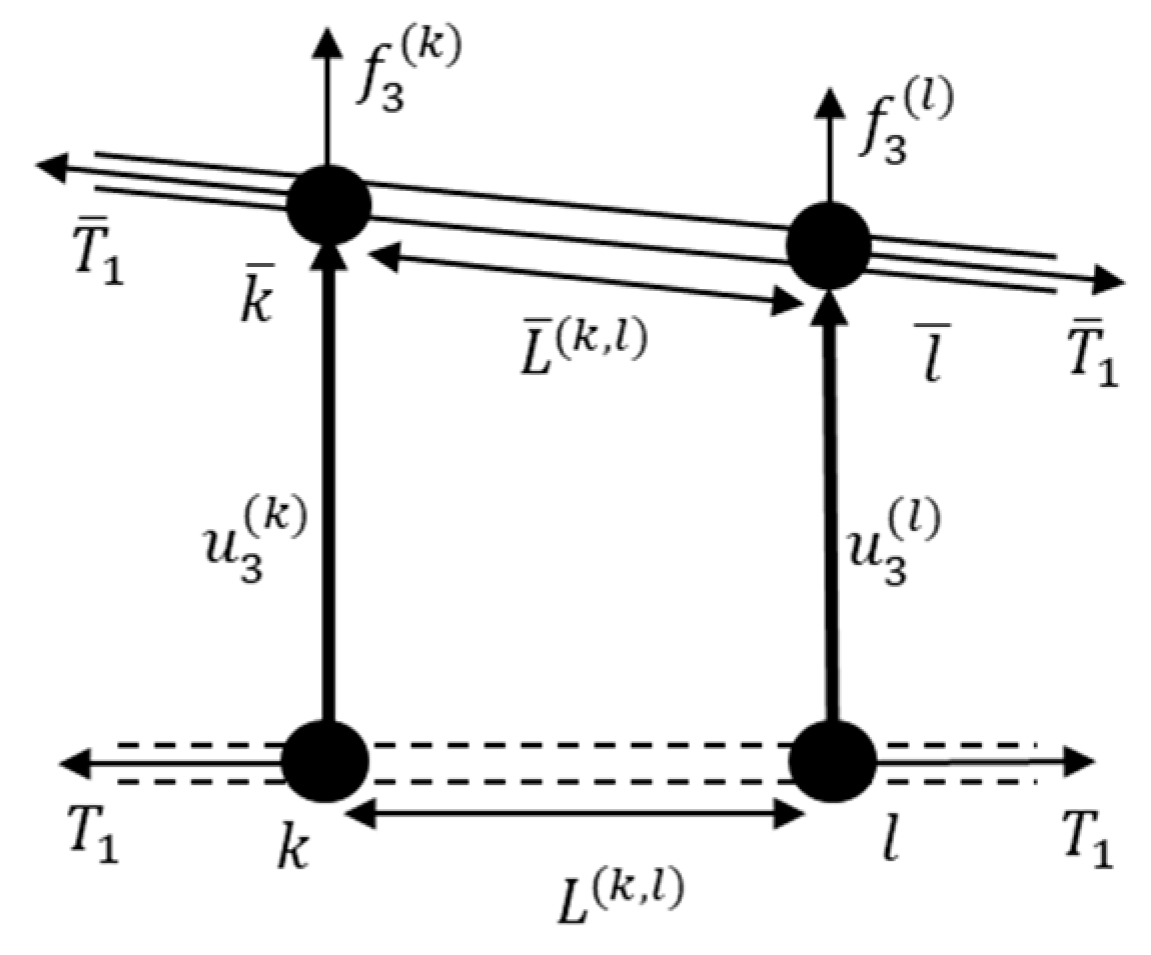
2. Materials and Methods
3. Results
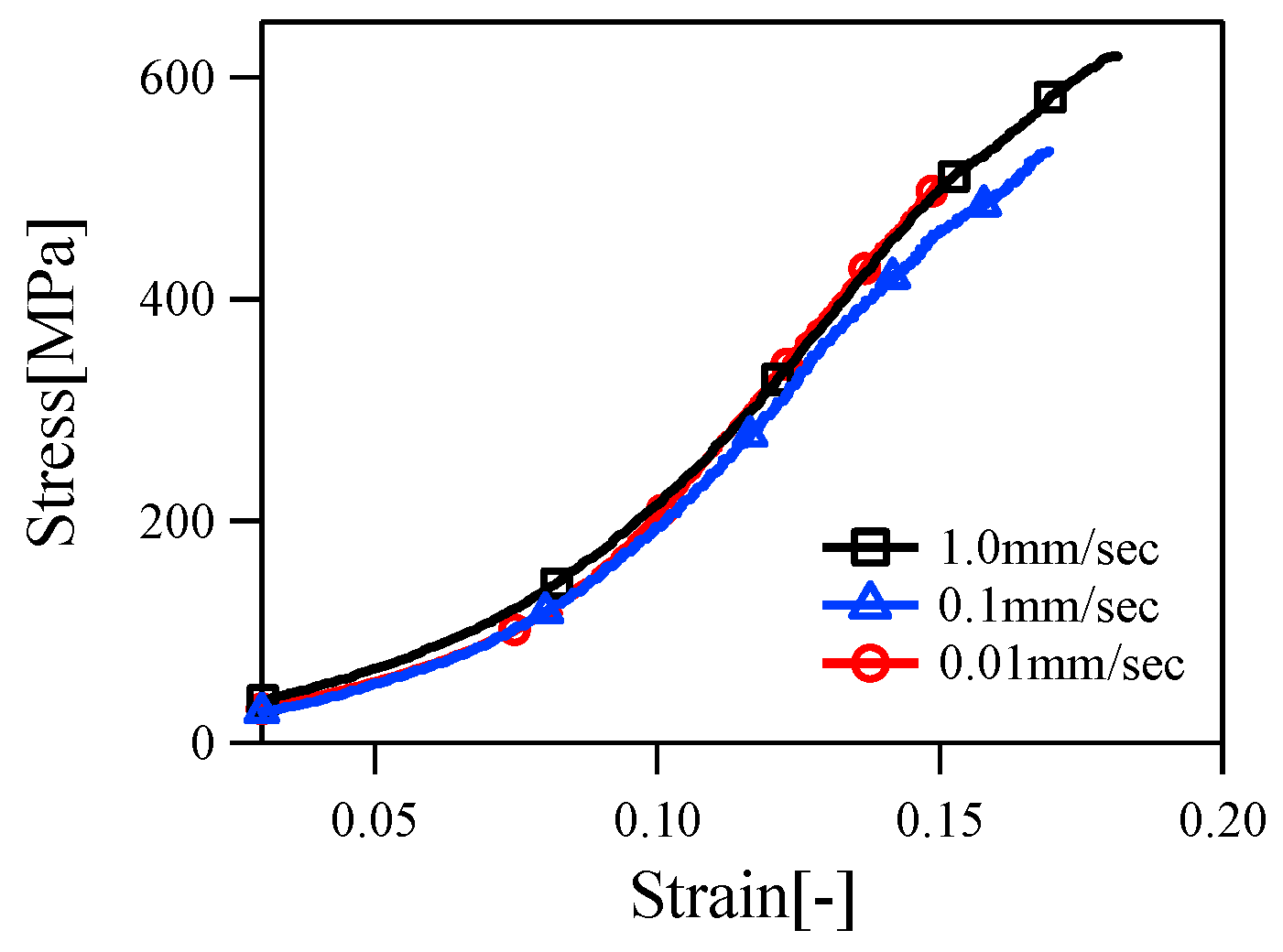
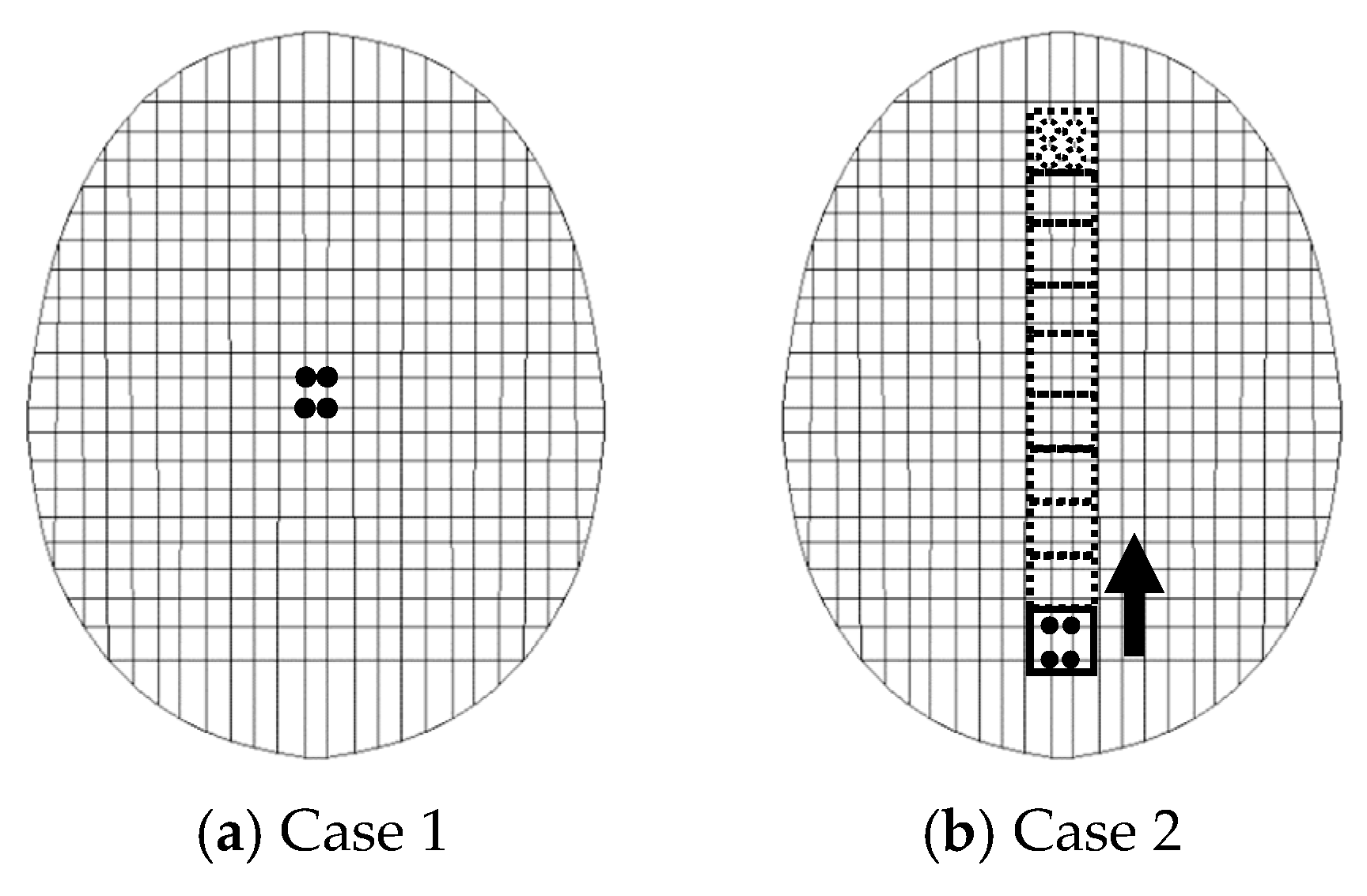
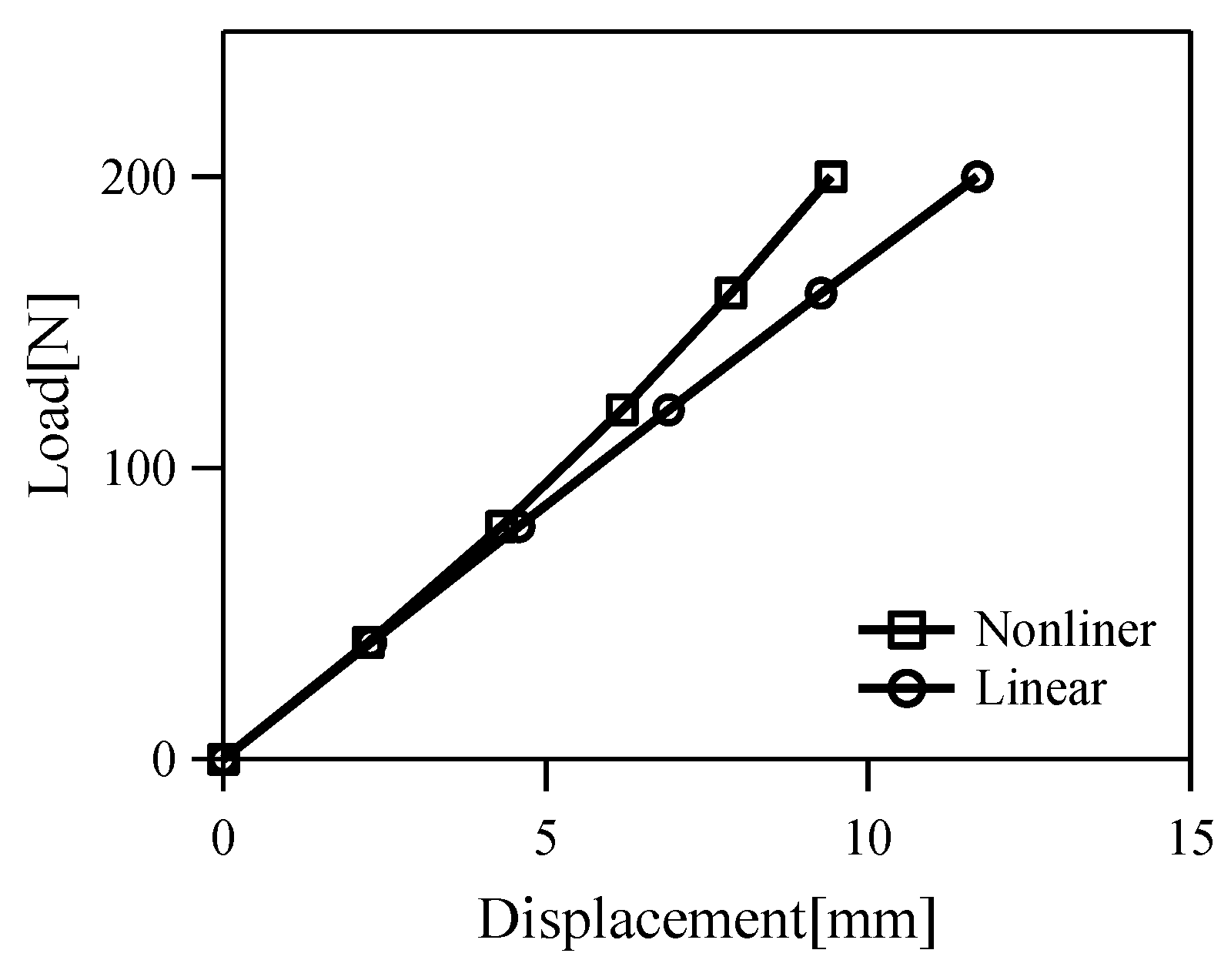
3.1. Loading Test of Nylon Strings
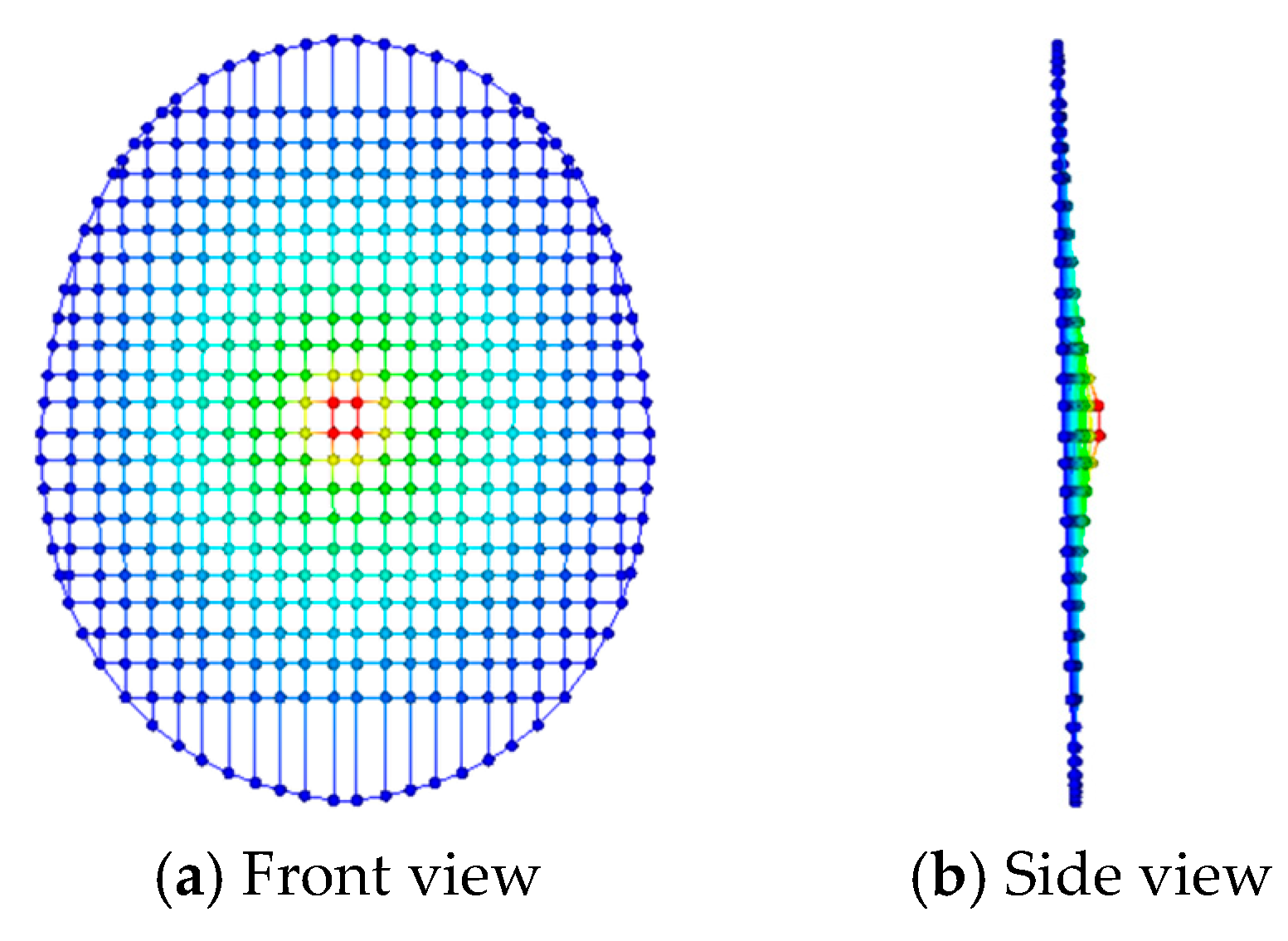
3.2. Analysis of the String Plane Models of Three Badminton Racquets
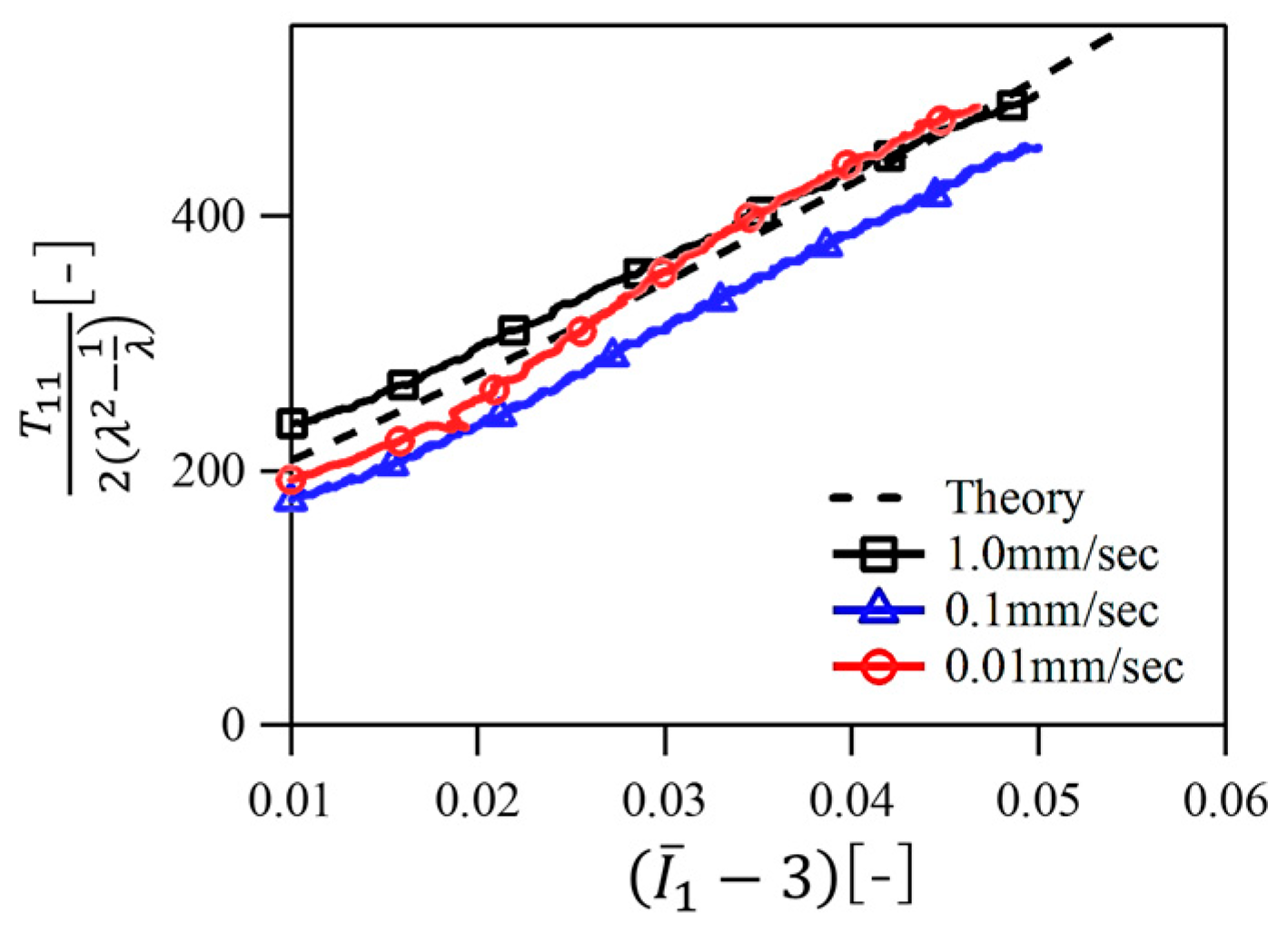
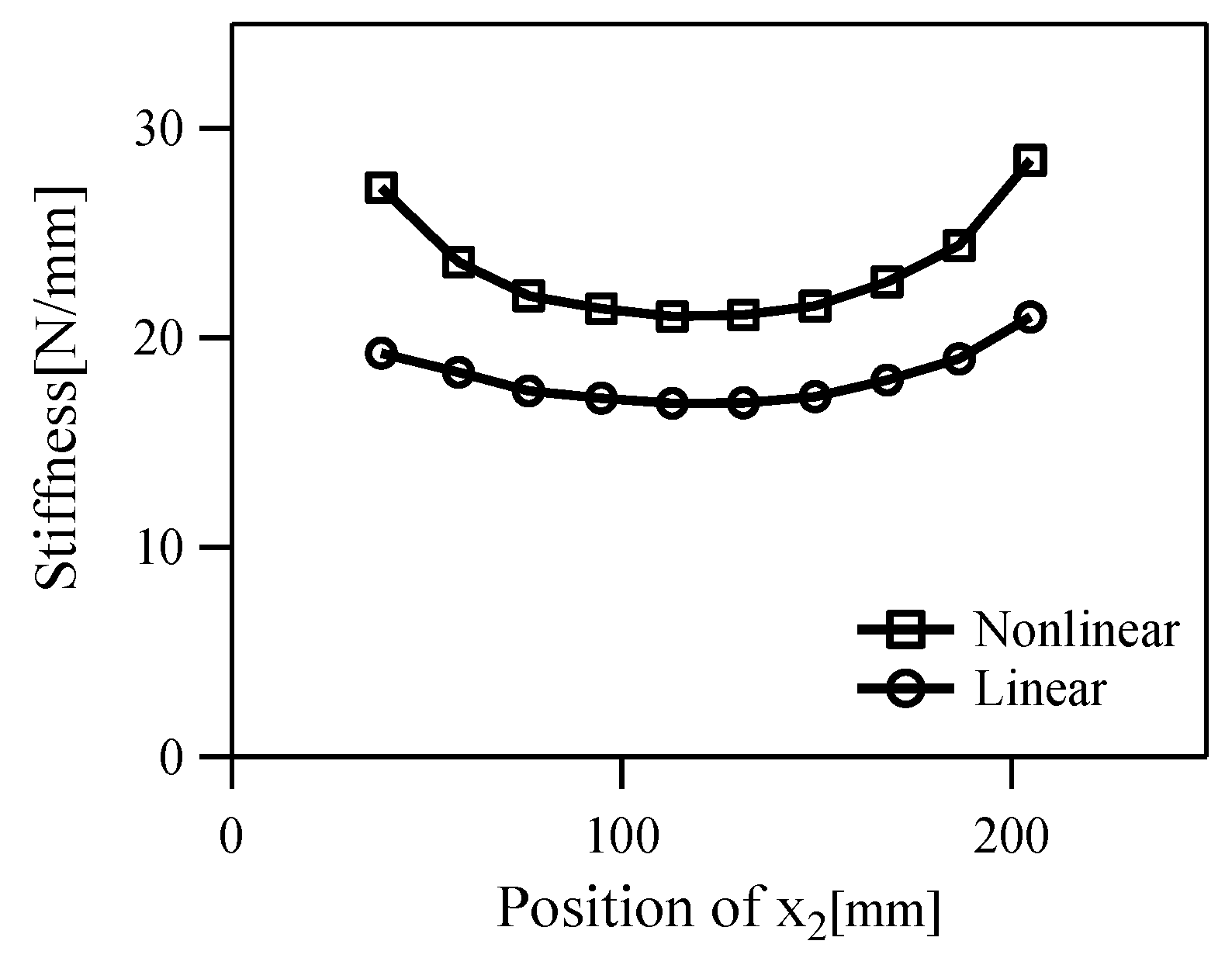
3.3. Effect of the Nonlinear Property of Polymer Strings
4. Discussion
5. Conclusions
References
- Kwan, M. Designing the World’s Best Badminton Racket. Ph.D. Thesis, Aalborg University, Aalborg, Denmark, 2010. [Google Scholar]
- Nasruddin, F.A.; Harun, M.N.; Syahrom, A.; Abdul Kadir, M.R.; Omar, A.H.; Oechsner, A. Finite Element Analysis on Badminton Racket Design Parameter, 1st ed.; Springer Informational Publishing: New York, NY, USA, 2016; pp. 27–32. [Google Scholar]
- Allen, T.; Choppin, S.; Knudson, D. A Review of Tennis Racket Performance Parameters. Sports Eng. 2016, 19, 1–11. [Google Scholar] [CrossRef]
- Li, L.; Yang, S.H.; Hwang, C.; Kim, Y.S. Effects of String Tension and Impact Location on Tennis Playing. J. Mech. Sci. Technol. 2009, 23, 2990–2997. [Google Scholar] [CrossRef]
- Blomstrand, E.; Demant, M. Simulation of a Badminton Racket. Master’s Thesis, Chalmers University of Technology, Göteborg, Sweden, 2017. [Google Scholar]
- Matsuda, A.; Nakui, M.; Hashiguti, T. Simulation of Mechanical Characteristics of Tennis Racket String Bed Considering String Pattern. Proceedings 2018, 2, 264. [Google Scholar]
- Martins, P.A.L.S.; Natal Jorge, R.M.; Ferreira, A.J.M. A Comparative Study of Several Material Models for Prediction of Hyperelastic Properties: Application to Silicone-Rubber and Soft Tissues. Strain 2006, 42, 135–147. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takizawa, M.; Matsuda, A.; Hashiguchi, T. A Study on the Mechanical Characteristics of String Planes of Badminton Racquets by Nonlinear Finite Element Analysis. Proceedings 2020, 49, 42. https://doi.org/10.3390/proceedings2020049042
Takizawa M, Matsuda A, Hashiguchi T. A Study on the Mechanical Characteristics of String Planes of Badminton Racquets by Nonlinear Finite Element Analysis. Proceedings. 2020; 49(1):42. https://doi.org/10.3390/proceedings2020049042
Chicago/Turabian StyleTakizawa, Masatomo, Akihiro Matsuda, and Tomohiro Hashiguchi. 2020. "A Study on the Mechanical Characteristics of String Planes of Badminton Racquets by Nonlinear Finite Element Analysis" Proceedings 49, no. 1: 42. https://doi.org/10.3390/proceedings2020049042
APA StyleTakizawa, M., Matsuda, A., & Hashiguchi, T. (2020). A Study on the Mechanical Characteristics of String Planes of Badminton Racquets by Nonlinear Finite Element Analysis. Proceedings, 49(1), 42. https://doi.org/10.3390/proceedings2020049042



