Abstract
A kinetic model of the shooting arms has estimated arm joint torques for one-hand set- and jump-shots in basketball. The dynamic model has three rigid planar links with rotational joints imitating an upper arm, forearm and hand with shoulder, elbow and wrist joints. In general shots controlled by hand, forearm and upper arm motions, there are many torque combinations of shoulder, elbow and wrist joints to produce shooters’ desired ball-release speed, angle and backspin angular velocity. The minimum of the sum of squares of the torque combinations exists at ball-release, when the release angular velocities of the hand and forearm are equal, and the release angular accelerations of the hand and forearm are also equal. Each torque of the shooting arm joints for the set-shot with upward shoulder speed is smaller than that for the jump-shot. Shoulder, elbow and wrist torques increase in proportion to horizontal shot distances. As release backspin angular speed increases, each of the shoulder, elbow and wrist torques also increases. The torques of the shoulder, elbow and hand affect the horizontal shot distance and the ball-release backspin.
1. Introduction
Skilled shooters relax their shooting arms and release the basketball with fingertip control, a gentle snap of the wrist, and a smooth shooting arm follow-through for one-hand set- and jump-shots. The ball is flipped, not pushed, at ball-release. In general shots controlled by hand, forearm and upper arm motions, suitable torque combinations at the shoulder, elbow and wrist may exist for the shooters’ desired ball-release speed, angle and backspin. Shot techniques with the minimum torques of the shooting arm joints allow them to make long-range shots with a high success rate.
Some previous basketball studies have commented on shooting arm mechanics depending on measured kinematic data [1,2,3,4]. These measurements achieved different results and conclusions because they measured different skill sets and situations. Biomechanical studies did not clearly identify the optimal coordination of human joint action [5] (p. 70). There have been few previous basketball studies that measured each torque of shooting arm joints for set- and jump-shot motions. Miller examined the patterns of the shooting arm muscles for shots at three different shot distances [6]. Dynamic models of shooting arms analyzed the corresponding joint torques for wheelchair basketball free throws [7].
A kinematic model has previously been used to analyze shooting arm motions at ball-release and to develop kinematic knowledge for set- and jump-shots [8,9,10]. The general jump-shot provides shooters with unlimited release conditions but they are required to control and coordinate correctly all shooting arm joints. Shoulder rotation contributes to vertical ball-release velocity, and elbow and wrist actions mostly produce the horizontal ball-release velocity and backspin when the hand and forearm are vertical at ball-release. The kinetic analysis estimates the torques of shooting arm joints, and reveals the relationships between the torques and the horizontal shot distance, and between the torques and backspin angular velocity. The dynamic model results allow new and useful instructions for players and coaches.
2. Shooting Arm Model, Simulation Parameters and Assumptions
Some previous biomechanical studies suggested that shooters should keep the ball center, wrist, elbow and shoulder joints in a vertical plane aligned with the target [5] (pp. 67–68). Figure 1 shows a shooting arm model similar to the two-dimensional three-segment model of Schwark et al. [7] (pp. 155–156). The Newtonian frame with unit vectors is fixed relative to the hoop center with the plane horizontal and the axis up. The ball is released a distance l away from and h below the hoop center with ball-release speed v, velocity angle from the horizontal plane, and backspin angular velocity . The shooting arm is assumed to move in the vertical plane and have three rigid links: upper arm, forearm and hand with rotational joints at the shoulder, elbow and wrist joints. Points, and represent the mass centers of links U, F, and H, respectively. Body, and points and denote the basketball, its center, and the shooter’s fingertip. Arm configuration is defined using counterclockwise angular displacements of the segments from the horizontal plane; of the upper arm; of the forearm; of the hand; and of the line including the fingertip and the ball center. Angles and are the counterclockwise angular displacements of the elbow and wrist, respectively.
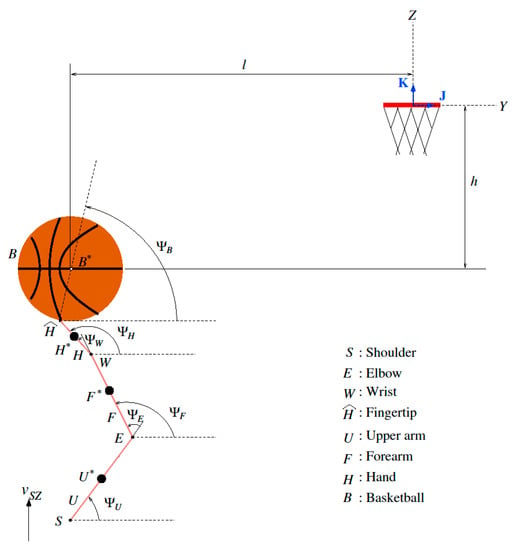
Figure 1.
Geometry of shooting arm motion with a basketball. The shooting arm model has three rigid planar links with rotational joints imitating an upper arm, forearm and hand with shoulder, elbow and wrist joints.
The lengths and masses of the hand, forearm and upper arm are calculated by using the measurements of De Leva [11] (p. 228) and the lengths m, m and m, and kg, kg and kg for a 191-cm guard player are chosen. The positions of the mass center of hand, forearm and upper arm are , and .
The equations of motion and the moment equations of the hand, forearm and upper arm can be written as
where , and are the mass moments of inertia of the hand, forearm and upper arm links, , and are the accelerations of the mass center of hand, forearm and upper arm, , and are the angular accelerations of the hand, forearm and upper arm, WH and WF are the reaction forces of the hand and forearm at the wrist, EF and EU are the reaction forces of the forearm and upper arm at the elbow, SU is the reaction force of the upper arm at the shoulder, is the moment of the hand about the wrist, and are the moments of the forearm about the wrist and elbow, and and are the moments of the upper arm about the elbow and shoulder.
The estimation of shooting arm motions at ball-release is based on some reasonable assumptions: the contact force vanishes at the fingertip [8] (p. 134) and the ball is released with the minimum ball-release speed [12] (pp. 358–359) in pure gravitational flight with no air drag; the shooter releases the ball without slipping between the fingertip and the ball surface at the fingertip contact point; the horizontal velocity and acceleration of the shoulder are zero; the vertical shoulder velocity is zero and positive for the jump- and set-shots, respectively; the angular displacements of the shooting arm and the ball are rad and rad, referred to in [7] (p. 445), and the angular velocities and accelerations of the hand and forearm are [7] (p. 446) and , respectively.
3. Results and Discussion
3.1. Torques and Angular Accelerations of Shooting Arm Joints at Ball-Release
The simulation chooses l = 4 m and rad/s, and h = 0.15 m, the upward shoulder speed = 0, v = 6.38 m/s andfor the jump-shot, and h = 0.6 m, = 2.4 m/s, v = 6.75 m/s andfor the set-shot. Figure 2a shows the relationships of shooting arm angular velocities for the jump- and set-shots at ball-release. The upper arm angular velocities at ball-release are constants; 21.1 rad/s and 12.5 rad/s for the jump- and set-shots, respectively. The hand and forearm angular velocities are negative. The direction of upper arm angular velocity is opposite to that of the hand and forearm. As upper arm angular speed increases, the shooter must produce larger hand and forearm angular speeds [10] (p. 5). The shooter is able to have many combinations of hand and forearm angular velocities. Points 1 to 5 represent possible hand and forearm angular velocity combinations. The shooter keeps the forearm vertical at point 1 with and rad/s for the jump-shot and with and rad/s for the set-shot. At point 5, the shooter manipulates the hand and forearm with the same angular velocity rad/s for the jump-shot and rad/s for the set-shot. Each combination of the hand and forearm angular velocities has many combinations of the angular acceleration and the torque of the arm joint shown in Figure 2b–d. Each of the hand and forearm angular velocity combinations has a constant upper arm angular acceleration of 1547.3 rad/s2 and 878.2 rad/s2 for the jump- and set-shot, respectively. Upper arm angular velocity and acceleration are unique for the release condition. Different shoulder torques can produce constant angular velocity and acceleration of the upper arm (Figure 2b). At ball-release, each of the torques is positive, the shoulder angular acceleration is positive, and the wrist and elbow angular accelerations are negative. The shooter is required to control and coordinate correctly all the upper arm, forearm and hand links, and is able to choose the torque combination with small torques at the shoulder, elbow and wrist joints.
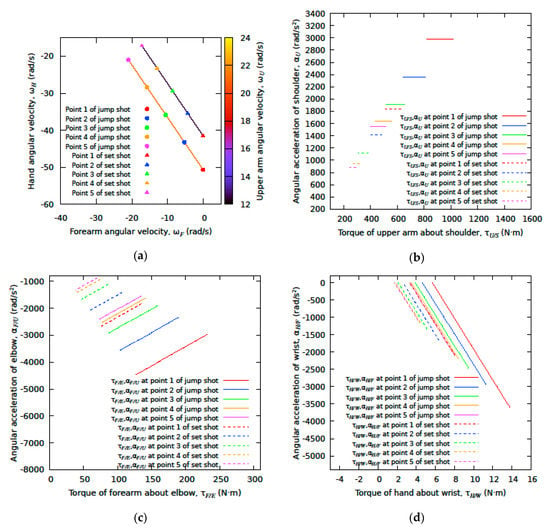
Figure 2.
Ball-release arm joint angular velocities, accelerations and torques for the 4 m set-shot with upward shoulder speed and for the jump-shot. Points 1 to 5 refer to the combinations of the hand and forearm angular velocity with the constant upper arm angular velocity. (a) Upper arm, forearm and hand angular velocities; (b) Angular acceleration of shoulder vs. torque of upper arm at shoulder joint; (c) Angular acceleration of elbow vs. torque of forearm at elbow; (d) Angular acceleration of wrist vs. torque of hand at wrist joint.
Figure 3 highlights the sum of squares of shoulder, elbow and wrist joint torques at ball-release for points 1 to 5 for the set- and jump-shot. Point A on the line of point 5 represents the minimum of the sum of squares of the torques at ball-release so that the shooter is able to swish with the smallest torques of the shooting arm joints. Point A indicates that the shooter should release the ball with the same hand and forearm angular velocity and the same hand and forearm angular acceleration. The set-shot with upward shoulder speed has a smaller sum of squares of arm joint torques than the jump-shot.
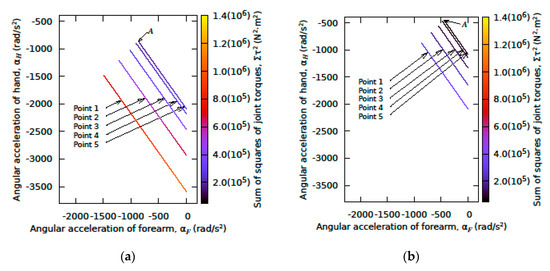
Figure 3.
Sum of squares of shoulder, elbow and wrist joint torques at ball-release as a function of angular accelerations of hand and forearm for points 1 to 5 of (a) the jump-shot and (b) the set-shot. Point A on the line of point 5 represents the minimum of the sum of squares of torques with (a) 3.32 Nm for the hand at the wrist, 73.6 Nm for the forearm at the elbow and 399.3 Nm for the upper arm at the shoulder, and with (b) 1.72 Nm for the hand at the wrist, 38.2 Nm for the forearm at the elbow and 229.9 Nm for the upper arm at the shoulder.
3.2. Torques for Shots with Different Horizontal Shot Distances at Ball-Release
Figure 4a shows the torques of the upper arm at the shoulder, the forearm at the elbow and the hand at the wrist and how they vary as a function of different horizontal shot distances for set- and jump-shots. The ball is released with the minimum release speed and the corresponding release angle based on [12] (pp. 358–359).
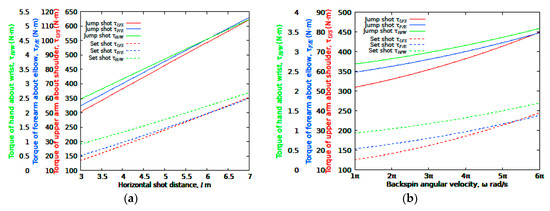
Figure 4.
Torques of the upper arm at the shoulder, the forearm at the elbow and the hand at the wrist at ball-release as a function of (a) horizontal shot distances and (b) backspin angular velocities. Each of the torques at the shoulder, elbow and wrist joints increases as horizontal shot distance increases or release backspin angular speed increases.
Upper arm angular speed increases in proportion to the horizontal shot distance for the set- and jump-shot [10] (pp. 3–5). Both the upper arm angular speed and the shoulder torque increase roughly linearly in proportion to the horizontal shot distance. Shoulder, elbow and wrist torques also increase in proportion to the horizontal shot distance, although Cooper and Siedentop instructed that the longer the distance from the hoop of the shot, the more pronounced the forearm pronation is [13] (p. 54).
3.3. Torques for Shots with Different Backspin Angular Velocity at Ball-Release
Knudson concluded that vigorous wrist flexion and pronation created backspin on the ball [5] (p. 72). In the general shot, hand and forearm actions mostly produce the horizontal ball-release speed and backspin angular velocity [8] (pp. 446–448). Figure 4b highlights the shoulder, elbow and wrist torques as a function of different release backspin angular velocities for the jump- and set-shot. Each of the torques at the shoulder, elbow and wrist joints increases as backspin angular speed increases. All shooting arm joint torques affect the backspin.
4. Conclusions
A kinetic model has estimated torques at shoulder, elbow and wrist joints at ball-release for set- and jump-shots. There are many shooting arm joint torque combinations for a given shooter’s desired ball-release speed, angle and backspin angular velocity. The shooter is required to control and coordinate correctly all the shoulder, elbow and wrist torques. In order to shoot the ball with the smallest torques of the shooting arm joints at ball-release, the shooter releases the ball with the same hand and forearm angular velocity and the same hand and forearm angular acceleration. This technique makes it possible to capture the ball for long-range shots. Shoulder, elbow and wrist joint torques all increase in proportion to the horizontal shot distance. All torques (at the shoulder, elbow and wrist) contribute to the ball-release backspin angular velocity.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Miller, S.; Bartlett, R. The effects of increased shooting distance in the basketball jump-shot. J. Sports Sci. 1993, 11, 285–293. [Google Scholar] [CrossRef] [PubMed]
- Miller, S.; Bartlett, R. The relationship between basketball shooting kinematics, distance and playing position. J. Sports Sci. 1996, 14, 243–253. [Google Scholar] [CrossRef] [PubMed]
- Okazaki, V.H.A.; Rodacki, A.L.F. Increased distance of shooting on basketball jump-shot. J. Sports Sci. Med. 2012, 11, 231–237. [Google Scholar] [PubMed]
- Tsarouchas, E.; Kalamaras, K.; Giavroglou, A.; Pressas, S. Biomechanical analysis of free shooting in basketball. In Proceedings of the 6th International Society of Biomechanics in Sports Symposium; Kreighbaum, E., McNeill, A., Eds.; International Society of Biomechanics in Sports: Bozeman, MT, USA, 1990; pp. 551–560. [Google Scholar]
- Knudson, D. Biomechanics of the basketball jump-shot—Six key teaching points. J. Phys. Educ. Recreat. Dance 1993, 64, 67–73. [Google Scholar] [CrossRef]
- Miller, S. Contribution of selected muscles to basketball shooting. In Proceedings of the 15th International Symposium on Biomechanics in Sports; Wilkerson, J., Ludwig, K., Zimmermann, W., Eds.; International Society of Biomechanics in Sports: Denton, TX, USA, 1997; pp. 475–481. [Google Scholar]
- Schwark, B.N.; Mackenzie, S.J.; Springings, E.J. Optimizing the release conditions for a free throw in wheelchair basketball. J. Appl. Biomech. 2004, 20, 153–166. [Google Scholar] [CrossRef]
- Okubo, H.; Hubbard, M. Kinematics of arm joint motions in basketball shooting. Procedia Eng. 2015, 112, 443–448. [Google Scholar] [CrossRef]
- Okubo, H.; Hubbard, M. Comparison of shooting arm motions. Procedia Eng. 2016, 147, 133–138. [Google Scholar] [CrossRef]
- Okubo, H.; Hubbard, M. Kinematic differences between set- and jump-shot motions in basketball. Proceedings 2018, 2, 201. [Google Scholar]
- De Leva, P. Adjustments to Zatsiorsky-Seluyanov’s segment inertia parameters. J. Appl. Biomech. 1996, 29, 1223–1230. [Google Scholar] [CrossRef]
- Brancazio, P.J. The physics of basketball. Am. J. Phys. 1981, 49, 356–365. [Google Scholar] [CrossRef]
- Cooper, J.M.; Siedentop, D. The Theory and Science of Basketball, 2nd ed.; Lea & Febiger: Philadelphia, PA, USA, 1975; pp. 64–71. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).