Modelling Bending Stiffness and Vibration Characteristics to Enable Simulation-Driven Ski Design †
Abstract
1. Introduction
2. Materials and Methods
2.1. The Ski Candide 3.0
2.2. Experimental Testing
2.2.1. Three-Point Bend Test for Stiffness Characteristics
2.2.2. Experimental Modal Analysis
2.3. Mechanical Modelling and Simulation
2.3.1. The Finite Element Model of the Ski
2.3.2. Load Cases
Three-Point Bend Test
Simulated Modal Analysis
3. Results
3.1. Three-Point Bend Test
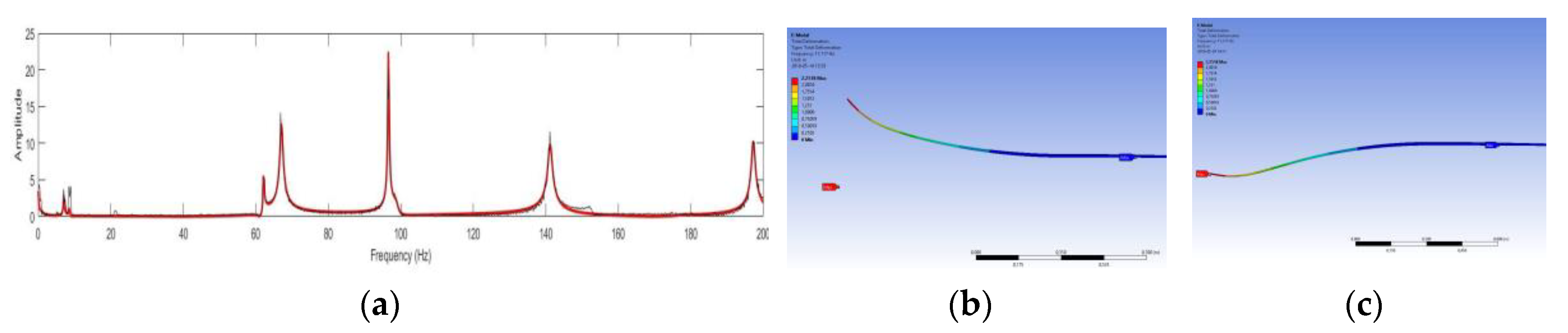
3.2. Modal Analysis
4. Concluding Remarks and Outlook
Acknowledgments
Conflicts of Interest
References
- Clerc, C.; Gaertner, R.; Trompette, P. Computer aided design of skis. Finite Elements Analysis Design 1989, 5, 1–14. [Google Scholar] [CrossRef]
- Nordt, A.A.; Springer, G.S.; Kollár, L.P. Computing the mechanical properties of alpine skis. Sports Eng. 1999, 2, 65–84. [Google Scholar] [CrossRef]
- Federolf, P.; Roos, M.; Lüthi, A. Finite Element Simulation of the Ski-Snow Interaction in a Carved Turn in Alpine Skiing. Sports Eng. 2010, 12, 123–133. [Google Scholar] [CrossRef]
- Wolfsperger, F.; Szabo, D.; Rhyner, H. Development of alpine skis using FE simulations. Procedia Eng. 2016, 147, 366–371. [Google Scholar] [CrossRef][Green Version]
- International Organization for Standardization. (2013). Alpine Skis — Determination of Elastic Properties. ISO Standard No. 5902. Available online: https://www.iso.org/standard/60844.html (accessed on 3 June 2020).
- Schwanitz, S.; Griessl, W.; Leilich, C.; Krebs, R.; Winkler, B.; Odenwald, S. The Effect of a Vibration Absorber on the Damping Properties of Alpine Skis. Proceedings 2018, 2, 305. [Google Scholar]
- Truong, J.; Brousseau, C.; Lussier Desbiens, A. A Method for Measuring the Bending and Torsional Stiffness Distributions of Alpine Skis. Procedia Eng. 2016, 147, 394–400. [Google Scholar] [CrossRef][Green Version]
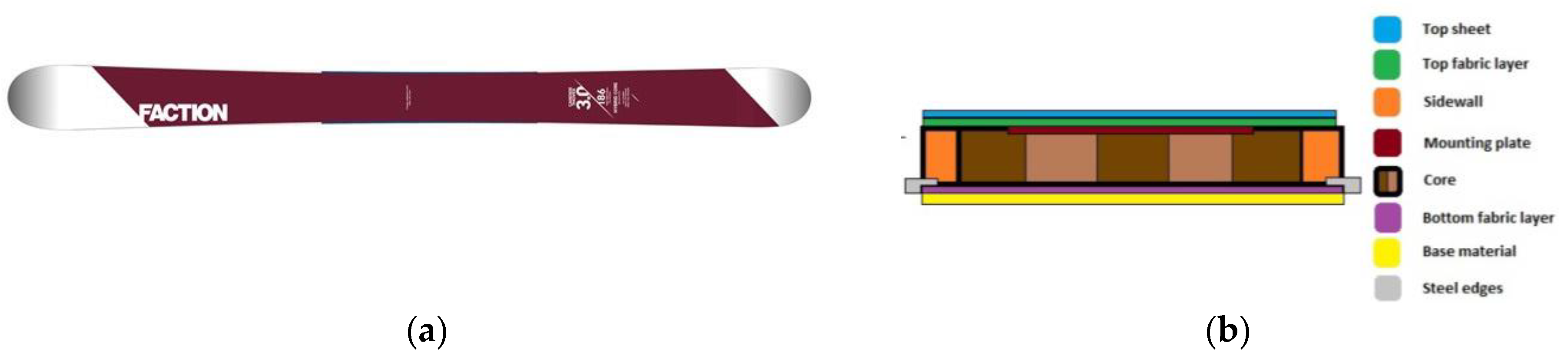




| Ski Lay-Up (Bottom to Top) | Longitudinal 1 Stiffness [GPa] | Density [kg/m3] |
|---|---|---|
| Top sheet | Very low stiffness, i.e., not included | 8050 |
| Top fabric layer | 25/352 | 2000 |
| Mounting plate (Titanal) | 72 | 2820 |
| Core (Poplar/Balsa/Ash/Beech/Paulownia) | 10.9/3.7/12.3/14.3/4.4 | 455/150/680/720/280 |
| Bottom fabric layer | 25/352 | 2000 |
| Base material (PE-UHMW) | 0.9 | 940 |
| Exp. Eigenfreq. (Hz) | Exp. Damp. Coeff. | Num. Eigenfreq.— High Stiffness (Hz) | Num. Eigenfreq.— Low Stiffness (Hz) |
|---|---|---|---|
| 9 | 0.0033 | 12 | 11 |
| 62 | 0.0017 | 54 | 49 |
| 67 | 0.0061 | 80 | 77 |
| 97 | 0.0098 | 110 | 106 |
| 141 | 0.0044 | 130 | 119 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borenius, J.; Edman, H.; Lindmark, A.; Pålsson, M.; Abrahamsson, T.; Fagerström, M. Modelling Bending Stiffness and Vibration Characteristics to Enable Simulation-Driven Ski Design. Proceedings 2020, 49, 157. https://doi.org/10.3390/proceedings2020049157
Borenius J, Edman H, Lindmark A, Pålsson M, Abrahamsson T, Fagerström M. Modelling Bending Stiffness and Vibration Characteristics to Enable Simulation-Driven Ski Design. Proceedings. 2020; 49(1):157. https://doi.org/10.3390/proceedings2020049157
Chicago/Turabian StyleBorenius, John, Henrik Edman, Albin Lindmark, Marcus Pålsson, Thomas Abrahamsson, and Martin Fagerström. 2020. "Modelling Bending Stiffness and Vibration Characteristics to Enable Simulation-Driven Ski Design" Proceedings 49, no. 1: 157. https://doi.org/10.3390/proceedings2020049157
APA StyleBorenius, J., Edman, H., Lindmark, A., Pålsson, M., Abrahamsson, T., & Fagerström, M. (2020). Modelling Bending Stiffness and Vibration Characteristics to Enable Simulation-Driven Ski Design. Proceedings, 49(1), 157. https://doi.org/10.3390/proceedings2020049157




