Bowling Performance Assessed with a Smart Cricket Ball: A Novel Way of Profiling Bowlers ^†

Abstract

Profiling of spin bowlers is currently based on the assessment of translational velocity and spin rate (angular velocity). If two spin bowlers impart the same spin rate on the ball, but bowler A generates more spin rate than bowler B, then bowler A has a higher chance to be drafted, although bowler B has the potential to achieve the same spin rate, if the losses are minimized (e.g., by optimizing the bowler’s kinematics through training). We used a smart cricket ball for determining the spin rate and torque imparted on the ball at a high sampling frequency. The ratio of peak torque to maximum spin rate times 100 was used for determining the ‘spin bowling potential’. A ratio of greater than 1 has more potential to improve the spin rate. The spin bowling potential ranged from 0.77 to 1.42. Comparatively, the bowling potential in fast bowlers ranged from 1.46 to 1.95.

1. Introduction

For the profiling of bowlers in cricket, two parameters are usually assessed and sufficient for decision-making, namely spin (angular velocity) and speed (translational velocity). This principle is applied at cricket centres [1], and also is reflected in the types of datasets generated by smart balls in general, such as: Mizuno smart baseball, iBall smart baseball, Strike smart baseball, and Kookaburra smart cricket ball. The limitation of this approach is the exclusive focus on the performance outcomes of spin bowlers without any assessment of efficiency. Strictly speaking, the efficiency is defined as the ratio of output to input and is usually an energy ratio. Although the input to a sporting action generated by the muscles is difficult to measure, the force or the torque applied by the human body to an object can be measured or calculated. The efficiency of a system is a performance parameter that has not been measured by current commercial smart balls, a fact that significantly detracts from their practical application. A measure related to efficiency will complement the standard performance outcomes generated by smart balls and provide a more valid basis for selecting bowlers into elite training squads.

The Smart Cricket Ball [2,3,4,5] was developed in 2011 to give coaches and bowlers a suite of tools, by outputting five physical parameters and five skill parameters (the latter are all related to efficiency). This is done at a high sampling frequency (815 Hz) throughout the course of the entire bowling action and flight phase of the ball, assessing spin bowling standards from a more rigorous biomechanics perspective.

The aim of this study is to develop and investigate a parameter that represents an efficiency equivalent, related to both torque and spin rate, and thus, to the bowling potential.

2. Materials and Methods

The smart cricket ball developed by [4,5] was trialled by different bowlers from amateur level to national team players. In total, 16 finger-spinners (ball released when supinating the forearm), 7 wrist-spinners (ball released when pronating the forearm), and 10 fast bowlers each bowled the Smart Ball 3–6 times, and their data were analysed from the parameters generated by the smart ball [6,7]. Within each group, only comparable deliveries were analysed: sidespin (off-spin) in finger-spinners, sidespin (leg-spin) in wrist-spinners, and seam bowling in fast bowlers. Although the bowling potential is more applicable to spin bowlers, fast bowlers were included for comparative reasons. This study was granted Ethics approval by the Swinburne University Human Ethics Committee (approval no. 20191582-3216) and adhered to the Declaration of Helsinki.

If the output parameter is the spin rate, then the input is provided by the torque imparted on the ball by the bowler. The ratio of peak torque to maximum spin rate reveals how economically the ball spin rate is increased. If two bowlers generate the same spin rate, but bowler A imparts a higher torque than bowler B, then bowler A’s bowling action is less economical, or less efficient, than the one of bowler B.

In order to investigate this principle, the ratio of peak torque (T_max) to maximum spin rate (ω_max) times 100 was calculated from the data of the 33 bowlers. As a theoretical rule of the thumb, a torque of 0.01 Nm is required to produce a spin rate of 1 rps, yielding a unity ratio (100·T_max/ω_max = 1), denoted the ‘bowling potential’. Note that the ‘bowling potential’ is valid for comparing bowlers who bowl the same delivery (e.g., off-spin, leg-spin, etc.), but invalid for comparing bowlers with different stock balls (e.g., finger-spin vs. wrist-spin; backspin vs. topspin). This result, 100·T_max/ω_max ~ 1 cNms, was found empirically and practically from experiments with the smart cricket ball. The higher the bowling potential, the lower is the efficiency. Efficiency and bowling potential are therefore inversely related. This means that a high torque has the potential to achieve a fast spin rate if bowlers are able to make use of it. If the torque is directly translated to spin rate without any losses, then the potential is used up. Note that torque peaks and angular velocity peaks do not occur at the same time.

The differences of 100·T_max/ω_max between the three groups (finger-spinners, wrist-spinners, fast bowlers) were tested with the Kruskal–Wallis rank sum test for multiple independent samples, with post hoc tests of Conover and Dunn, both with p-values adjusted by the Holm FWER (familywise error rates) and Benjamini–Hochberg FDR (false discovery rate) methods. For significance testing, α was set to 0.05.

3. Results

The maximum torque against maximum spin rate plot is shown in Figure 1. The gradient of each of the three groups represents the bowling potential. Bowlers located above and to the left of the gradient line have a greater bowling potential, but also a smaller efficiency.

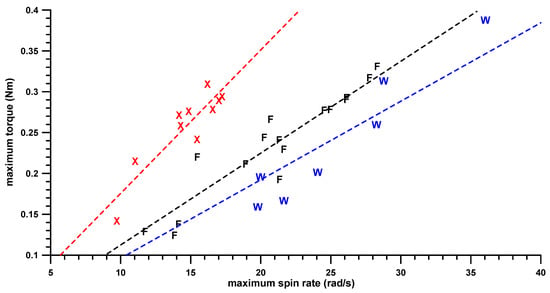
Figure 1. Maximum torque against maximum spin rate; dashed line = gradient of a through-origin fit (times 100 = average bowling potential of each group): X = fast bowlers, F = finger-spinners, W = wrist-spinners.

The following statistical data of 100·T_max/ω_max were found (average ± standard deviation, minimum–maximum):

−

finger-spinners: 1.12 ± 0.13 cNms (0.90–1.42);

−

wrist-spinners: 0.92 ± 0.13 cNms (0.77–1.09);

−

fast bowlers: 1.75 ± 0.16 cNms (1.46–1.95).

The box-whisker plot of the data distribution within each group is shown in Figure 2.

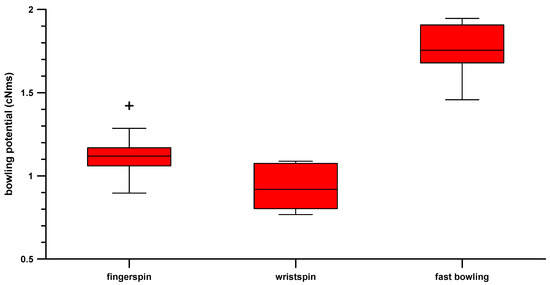
Figure 2. Box and whisker-plot of the bowling potential within each group (in cNms, centi-Newton-meter-second); + = outlier.

The Kruskal–Wallis rank sum test for the three independent samples was significant (p = 5.00∙10⁻⁶). The p-values of all post hoc tests were smaller than 0.05, i.e., between 0.044 and 5.51∙10⁻¹⁰. Therefore, the three average values of 100·T_max/ω_max are all significantly different from each other.

The bowling potential within each group varied greatly (Figure 2), across ranges of 0.52 cNms in finger-spinners, 0.32 cNms in wrist-spinners, and 0.49 cNms in fast bowlers.

4. Discussion

From previous research [4], it is known that wrist-spin deliveries are more efficient than finger-spin ones, whereas backspin (fast bowling) deliveries are the least efficient. This explains why the average 100·T_max/ω_max of wrist-spinners was slightly smaller than 1; the one of finger-spinners was slightly greater than 1; and the one of fast bowlers exceeded 1.5. Considerable individual differences existed between different bowlers, within the same group of delivery. For example, the best wrist-spinner had a spin rate of 36.05 rps, and a bowling potential of 1.09 cNms, whereas the wrist-spinner with the smallest (best) ratio (0.77 cNms, 30% less) produced a spin rate of ‘only’ 21.66 rps. Thus, the ratio reveals more of the potential and the skill of a bowler rather than the spin rate does; note that ‘more potential’ means ‘less skill’.

As already mentioned in the Methods section, the bowling potential is more applicable to spin bowlers rather than to fast bowlers. Fast bowlers were included in this study only for comparative reasons. For fast bowlers, speed is more important than spin.

The ‘potential’ is also applicable to baseball in terms of a pitching potential. A striking example is exemplified by [8], where a potential of 2.52 cNms was found in a pitcher. The latter threw the baseball version of the smart cricket ball, used in this study, for delivering a fastball, comparable to a fast bowling delivery in cricket. The pitcher produced a spin rate of 15.70 rps from a torque of 0.40 Nm. If this pitcher were a wrist-spinner, then a 0.4 Nm torque would generate an average maximum spin rate of 43.5 rps (100·0.4/0.92 = 43.5).