Abstract
The development of systematic coarse-grained mesoscopic models for complex molecular systems is an intense research area. Here we first give an overview of different methods for obtaining optimal parametrized coarse-grained models, starting from detailed atomistic representation for high dimensional molecular systems. We focus on methods based on information theory, such as relative entropy, showing that they provide parameterizations of coarse-grained models at equilibrium by minimizing a fitting functional over a parameter space. We also connect them with structural-based (inverse Boltzmann) and force matching methods. All the methods mentioned in principle are employed to approximate a many-body potential, the (n-body) potential of mean force, describing the equilibrium distribution of coarse-grained sites observed in simulations of atomically detailed models. We also present in a mathematically consistent way the entropy and force matching methods and their equivalence, which we derive for general nonlinear coarse-graining maps. We apply, and compare, the above-described methodologies in several molecular systems: A simple fluid (methane), water and a polymer (polyethylene) bulk system. Finally, for the latter we also provide reliable confidence intervals using a statistical analysis resampling technique, the bootstrap method.
1. Introduction
The enormous range of length and time scales involved in complex materials presents a challenging computational task, mainly, due to a wide range of relaxation times. A standard methodology to overcome problems of long relaxation times is to abandon the chemical detail and describe the molecular system by fewer degrees of freedom. Thus, systematic coarse-grained (CG) models are developed by averaging out the details at the molecular level, and by representing groups of atoms by a single CG particle. The challenge is to derive reliable coarse models both for reproducing the structural and the dynamical properties of systems. That is, to identify and effective approximate force field, approximating the potential of mean force (PMF), and then approximations to kinetic coefficients such as the friction.
Methods to approximate the PMF are well studied in the literature. Examples include: (a) The Boltzmann inversion methods, also known as structural-based, which rely on matching the radial distribution function [1,2,3,4,5,6]. (b) The information theory based variational inference method relies on the minimization of the relative entropy (RE) between the configurational distributions of the system and the approximate one, [7,8,9,10]. (c) The Force Matching (FM) relies on minimizing the distance between the forces exerted on the CG particles and the approximate ones [11,12,13]. Recently, we have introduced a path-space variational inference methods were introduced, capable of inferring dynamical models of coarse-grained systems, [9,14]. There the Relative Entropy Rate (RER) is defined as the appropriate quantity to infer the coarse dynamics for stationary system, while the path space force matching is introduced.
The purpose of the current work is to present a short review of the information theoretic methodologies ( relative entropy, and relative entropy rate) and their relation to the force matching and path-space force matching methodologies, through the application to different molecular systems.
2. Methodology
Let a prototypical problem of N classical atoms in a box of volume V at temperature T. We denote ∈ the position vector and ∈ the momentum vector of the N atoms. The probability of an elementary configuration is given by the Gibbs probability,
where is potential energy of a state , Zis the normalization constant (partition function), and with the Boltzmann constant and T the temperature. In the above relation the kinetic part of the Hamiltonian has been integrated out. Coarse-graining (CG) is a standard methodology to overcomes the large range of length and time scales by averaging out the details of the atomistic level at the molecular level through representing groups of atoms by a single particle. The CG map determines the position vectors of M CG particles (or beads) . Note that but still . From now on, we will use the bar "" notation for objects related to the CG model. The probability that the CG system has configuration is given by
The quantity
is the body potential of mean force (PMF). The corresponding conservative force is thus . While the above formula is exact, the accurate calculation of the PMF for a realistic model of a complex molecular system is a challenging task. This challenge is due to the high dimensionality of the integral, and the M vector as well.
Therefore, we develop methods to find an effective potential in a parameterized form, which best approximates the PMF, i.e.,:
Moreover, we assume that the evolution of the particles is described by a continuous time process , with path space distribution , and invariant measure the Gibbs probability, Equation (1). The approximate coarse space dynamics we adopt are described by a Markov process in with a parametric path space distribution .
2.1. Information Theoretic Variational Inference: The Relative Entropy
Here we adopt the information theoretic variational inference approach as the methodology to derive optimal approximate coarse models bot at equilibrium and dynamical regimes. This variational approach encompasses the minimization of the Relative Entropy (RE) between probability measures. The relative entropy (Kullback-Leibler divergence), [15], of two probability measures and on a common measurable space is given by
provided , i.e., P is absolutely continuous with respect to Q, and otherwise. The functional defines a pseudo-distance between two measures as and if and only if , P-a.s. In the case these probability measures have corresponding probability densities and Equation relent1 becomes . The optimization problem in path-space is,
where denotes the push-forward of the microscopic measure . When the system is at equilibrium the optimization principle is
When considering continuous time observations, in work [14] we prove that the path-space minimization principle (3) reduces to the path-space force matching (PSFM). In stationary dynamics the Relative Entropy Rate (RER) is defined by
where P and Q denote the corresponding stationary processes.
For discrete time observations (a) from the microscopic Gibbs density or (b) the path-space distribution at dynamical regimes, consideringthe estimator for the RE, the optimal parameter estimate is given by [14],
and are the microscopic and coarse space transition probability densities of the Markov processes and , respectively. Note that if the time series are stationary, the RER optimization is
2.2. Relative Entropy and Force-Matching
The Force-Matching (FM) method estimates an effective CG potential that reproduces best the potential at the reference all-atom system, by solving the optimization problem
i.e., we minimize the average difference between the atomistic forces and the corresponding CG forces , where denotes the Euclidean norm in and denotes the expectation with respect to the probability Gibbs measure . The minimization problem for the discrete observations, and the linear parametric representation of the force , is
The path-space force matching optimization problem is, [14],
for which the discrete optimization problem becomes
2.3. Relative Entropy and Structural-Based Methods
The structural-based methods, such as the direct inverse Boltzmann (DBI), iterative Boltzmann inversion (IBI), and inverse Monte Carlo (IMC) methods, use the pair correlation function and the assumption that the interactions depend only on the distance R between particles, that is . is called the radial distribution function. Thus the CG effective interaction is given by
where
that is the average density of finding the CG particle 1 at a distance R from the particle 2.
The structural methods are thus based on the pair correlation function between CG particles, in contrast to the RE which is considering the joint probability distribution of the CG particles. In case the PMF can be exactly described by pair functions then the RE and structural methods coincide.
3. Results and Discussion
In the current section, we present the application of the variational inference methods, the RE, and the FM, for representative molecular systems: A simple fluid (bulk methane), a system of water molecules, and a polyethylene melt, at equilibrium conditions. We moreover study the bulk methane system out-of equilibrium, specifically we apply the PSFM at a transient time regime.
3.1. Bulk Methane
The molecular system consists of 666 methane molecules at temperature , and . We employed molecular dynamics simulations to generate the microscopic space data based on which we applied the inference methods. Details on the atomistic simulations are given in [16]. For the coarse-grained representation of methane we have used a one-site representation with a pair potential. The pair potentials we have tested are (a) expansions with linear and cubic B-splines (with 48 parameters) and (b) the Lennard–Jones parametric form (with two parameters).
A comparison of the FM, and IBI methods is depicted in Figure 1 [17]. The result depicts slight difference of the FM method to the RE and IBI. Figure 2 presents the performance of the FM and PSFM methods at equilibrium verifying the validity of the PSFM and its reduction to the FM method. A study at transient time regimes is presented in work [16].
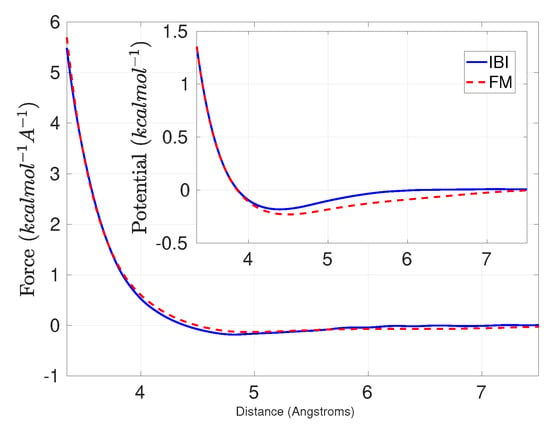
Figure 1.
Methane: The effective pair potential for a one-site methane melt, derived with the FM with cubic splines, and the IBI methods, at K.
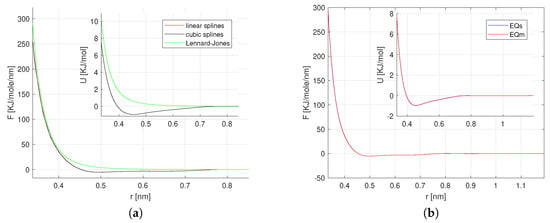
Figure 2.
Methane: The FM and the path-space force matching (PSFM) methods at equilibrium. (a) The FM pair force with linear and cubic B-splines, and Lennard–Jones parametrizations. (b) The PSFM reproduces the FM method, [16].
3.2. Water
The model system consists of 1192 molecules at ambient conditions (, ). Details on the atomistic simulations are given in [17]. For the coarse-grained representation of , we have also used a one-site representation with a pair potential. Figure 3a depicts the resulting pair potential obtained with the RE and FM methods. The RE and FM potentials have a very similar structure with two minima, though the actual values of the potential are different. Figure 3b shows that the pair correlation function derived by CG simulations with the RE potential and the target one (from atomistic simulations) are very close. That is, the RE potential can reproduce with sufficient accuracy the pair correlation.
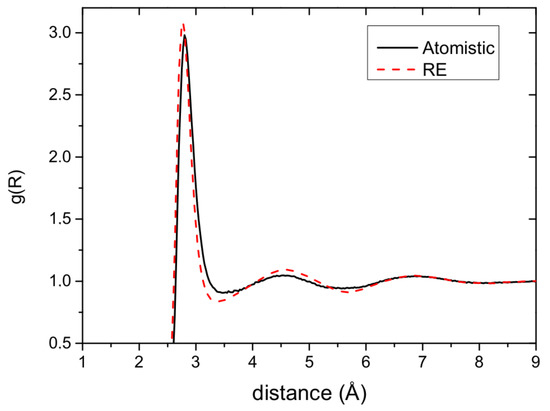
Figure 3.
Water: RE derived potential reproduces well the target pair correlation.
3.3. Polyethylene Melt
The model system consists of 96 polyethylene chains of 99 monomer units ( ), i.e., . The simulations were performed under NVT conditions at temperature . For the coarse-grained representation we consider a 3:1 mapping representation, i.e., three monomer units form one CG particle. With this application we study the effect of the size of the available observations (system configurations), and quantify uncertainties due to the small number of observations. Figure 4 depicts the derived FM potential for a large set of observations. In addition, shows the confidence set obtained with a statistical analysis resampling technique (bootstrap method) of a small observations set, which captures the large-set outcome.
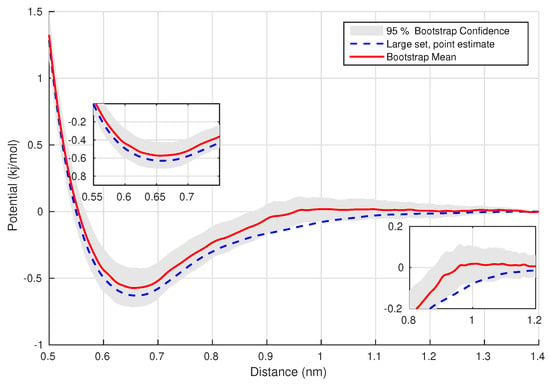
Figure 4.
Polyethylene: The FM potential for linear B-splines, for a set of 5000 observations and the 95% Bootstrap Confidence interval for the FM potential, with a set of 300 observations.
4. Conclusions
In the current work we presented a short review of the information theoretic variational inference method for coarse-graining molecular systems, for systems at- and out-of- equilibrium. Moreover, we presented the connection to the Force Matching method and its relation to the structural based methods. The application of all methods to the methane system shows that the RE and IBI methods give similar results while the FM differs slightly. While for the water model the RE and FM resulting potentials differ substantially, which is not surprising as we know that the two methods are equivalent only asymptotically. We verify the validity of the PSFM, i.e., deriving the piar potential using time-series data, since it produces the same results to the FM, i.e., with identically distributed data. Finally, with the application to the polyethylene system, we show that when the availability of observations is limited the bootstrapping method can provide reliable confidence intervals to the pair potential.
Funding
E.K. acknowledges support by the Hellenic Foundation for Research and Innovation (HFRI) and the General Secretariat for Research and Technology (GSRT), under grant agreement No [52].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Soper, A. Empirical potential Monte Carlo simulation of fluid structure. Chem. Phys. 1996, 202, 295–306. [Google Scholar] [CrossRef]
- Lyubartsev, A.P.; Laaksonen, A. On the Reduction of Molecular Degrees of Freedom in Computer Simulations. In Novel Methods in Soft Matter Simulations; Karttunen, M., Lukkarinen, A., Vattulainen, I., Eds.; Lecture Notes in Physics; Springer: Berlin, Germany, 2004; Volume 640, pp. 219–244. [Google Scholar] [CrossRef]
- Tschöp, W.; Kremer, K.; Hahn, O.; Batoulis, J.; Bürger, T. Simulation of polymer melts. I. Coarse-graining procedure for polycarbonates. Acta Polym. 1998, 49, 61. [Google Scholar] [CrossRef]
- Müller-Plathe, F. Coarse-Graining in Polymer Simulation: From the Atomistic to the Mesoscopic Scale and Back. ChemPhysChem 2002, 3, 754–769. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Adhikari, N.P.; van der Vegt, N.F.A.; Kremer, K. Hierarchical Modeling of Polystyrene: From Atomistic to Coarse-Grained Simulations. Macromolecules 2006, 39, 6708. [Google Scholar] [CrossRef]
- Briels, W.J.; Akkermans, R.L.C. Coarse-grained interactions in polymer melts: A variational approach. J. Chem. Phys. 2001, 115, 6210. [Google Scholar]
- Shell, M. The relative entropy is fundamental to multiscale and inverse thermodynamic problems. J. Chem. Phys. 2008, 129, 144108. [Google Scholar] [CrossRef] [PubMed]
- Chaimovich, A.; Shell, M.S. Anomalous waterlike behavior in spherically-symmetric water models optimized with the relative entropy. Phys. Chem. Chem. Phys. 2009, 11, 1901–1915. [Google Scholar] [CrossRef]
- Katsoulakis, M.A.; Plecháč, P. Information-theoretic tools for parametrized coarse-graining of non-equilibrium extended systems. J. Chem. Phys. 2013, 139, 4852–4863. [Google Scholar] [CrossRef] [PubMed]
- Kalligiannaki, E.; Harmandaris, V.; Katsoulakis, M.; Plecháč, P. The geometry of generalized force matching and related information metrics in coarse-graining of molecular systems. J. Chem. Phys. 2015, 143. [Google Scholar] [CrossRef] [PubMed]
- Izvekov, S.; Voth, G. Effective force field for liquid hydrogen fluoride from ab initio molecular dynamics simulation using the force-matching method. J. Phys. Chem. B 2005, 109, 6573–6586. [Google Scholar] [PubMed]
- Noid, W.G.; Liu, P.; Wang, Y.; Chu, J.; G. S. Ayton S. Izvekov, H.A.; Voth, G. The multiscale coarse-graining method. II. Numerical implementation for coarse-grained molecular models. J. Chem. Phys. 2008, 128, 244115. [Google Scholar] [CrossRef] [PubMed]
- Rudzinski, J.; Noid, W. Coarse-graining entropy, forces, and structures. J. Chem. Phys. 2011, 135, 214101. [Google Scholar] [CrossRef] [PubMed]
- Harmandaris, V.; Kalligiannaki, E.; Katsoulakis, M.; Plecháč, P. Path-space variational inference for non-equilibrium coarse-grained systems. J. Comput. Phys. 2016, 314, 355–383. [Google Scholar] [CrossRef]
- Cover, T.; Thomas, J. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 1991. [Google Scholar]
- Baxevani, G.; Kalligiannaki, E.; Harmandaris, V. Study of the transient dynamics of coarse-grained molecular systems with the path-space force-matching method. Procedia Comput. Sci. 2019, 156, 59–68. [Google Scholar] [CrossRef]
- Kalligiannaki, E.; Chazirakis, A.; Tsourtis, A.; Katsoulakis, M.; Plecháč, P.; Harmandaris, V. Parametrizing coarse grained models for molecular systems at equilibrium. Eur. Phys. J. Special Top. 2016, 225, 1347–1372. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).