Abstract
For several years, the requirements on miniaturization of electronic implants with application in functional electrostimulation have been increasing, while functionality and reliability should not be impaired. One solution concept is to use neither active electronic components nor sensors or batteries. Instead, the functionalities are ensured by the use of intrinsic nonlinear properties of the already used components and energy is transferred by inductive coupling. In this paper, ceramic capacitors are investigated as a first step towards exploiting the nonlinear characteristics of ferroelectric materials. The ceramic capacitors are characterized by simulation and measurements. The modeling is carried out in Mathcad Prime 3.1 and ANSYS 2019 R2 Simplorer and different solvers are compared for exemplary calculations. Finally, a measurement setup is realized to validate the models. Calculations show that the trapezoid method with a number of 500 k points in the given solution interval is best suited for ANSYS. In Mathcad, the Adams, Bulirsch–Stoer, Backward Differentiation Formula, Radau5, and fourth order Runge–Kutta methods with an adaptive step width and a resolution of 50 k points are the most suitable. The nonlinear properties of ferroelectric materials in ceramic capacitors modeled with these methods using ANSYS and Mathcad show small and equal deviation from the measurements.
1. Introduction
In the last few years, there has been a need for miniaturization of implantable systems used in functional electrostimulation without impairing functionality and reliability. Numerous implantable systems, such as the retinal implants Argus II (Second Sight Medical Products Inc., Sylmar, CA, USA), IRIS II (Pixium Vision S.A., Paris, France), Alpha AMS (Retina Implant AG, Reutlingen, Germany) [1], the vagus nerve stimulators AspireSR and SenTivaTM (LivaNova PLC, London, UK) [2], or the hypoglossal nerve stimulator from Inspire Medical Systems [3], are nowadays used to treat diseases such as retinitis pigmentosa, age-related macular degeneration, epilepsy, depression, pain, tinnitus, and obstructive sleep apnea. Due to the myriad of active electronic components, sensors, and bulky battery units in the majority of today’s implantable systems for functional electrostimulation, these cannot be implanted at the location where the electrical stimulation pulses need to be applied. Therefore, the electrodes for electrostimulation are connected to the implant electronics by wires, which are susceptible to migration and fracture over time [4]. In addition, malfunctions of the highly engineered implant electronics can also occur and an age-related replacement of the battery may be necessary over time [5]. From this point of view, electrical implants consisting only of passive components would be advantageous in terms of miniaturization and reliability, but the question arises how functionalities can be achieved without the use of active electronic components. The use of the intrinsic nonlinear properties of the components to be used anyway in implant electronics could answer this question. Thus, for example, in the context of functional electrostimulation, the stimulation current in an implant could be determined using the junction capacitance of a rectifier diode without having to use sensors or other active electronic components [6]. Another notable example is the so-called "Neural Dust" sensors. With a length of 3 mm and a cross-section of 1 mm², these sensors allow wireless acquisition of neural signals using the intrinsic properties of a piezo element [7]. The electronic implants considered in this paper contain neither batteries nor sensors or active electronic components and are consequently not suitable for autonomous operation. An extracorporeal wearable device is required for powering the implants. Powering is carried out by means of an inductive power supply at frequencies below 1 MHz. The amount of inductively transferred energy directly impacts the induced voltage. The sensor functionality of the further concept of this work is based on the indirect sensing of the induced voltage necessary for the power supply of the implant electronics by means of a change of its nonlinear electrical capacitance. In order to realize this sensor functionality, the intrinsic and nonlinear properties of the capacitors used must first be mastered. The aim of this paper is to establish a model allowing the modeling of nonlinear properties of ferroelectric materials under consideration of different calculation methods.
2. Methods
The modeling of the nonlinear properties of ferroelectric materials in ceramic capacitors was implemented in the circuit shown in Figure 1 using the capacitors C2a and C2b. The nonlinear characteristic of the ceramic capacitors was measured and used in Mathcad Prime 3.1 (PTC, Boston, MA, USA) and ANSYS 2019 R2 Simplorer (ANSYS, Inc., Canonsburg, PA, USA). The system consisted of an extracorporeal primary side carried by the patient which provided the inductive energy supply (see Figure 1a) and a secondary side implanted in the patient which converted the inductively received energy into stimulation pulses (see Figure 1b).
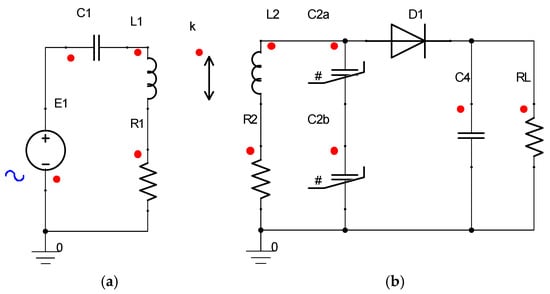
Figure 1.
Representation of the inductively coupled system for energy transmission in ANSYS: (a) primary side consisting of an ideal voltage source E1 and a series resonant circuit consisting of a capacitor C1, an inductance L1, and a loss resistor R1; (b) secondary side consisting of the implant electronics, which has a parallel resonant circuit which is composed of the inductance L2, the nonlinear capacitors C2a and C2b connected in series, and the loss resistance R2, a rectifier consisting of the diode D1 and the capacitor C4, and an ohmic load RL resulting from the biological tissue and electrode properties. The inductive coupling between the primary and secondary inductances is represented by the coupling factor k.
The inductively coupled system for energy transfer was described by the first order differential Equations (1)–(10):
where:
- : inductive coupling factor between the inductances L1 and L2;
- : amplitude of the sinusoidal voltage ;
- : angular frequency of the sinusoidal voltage ;
- : electrical current across the primary resonant circuit;
- : electrical voltage across the capacitor C1;
- : electrical current across inductance L2 and its loss resistance R2;
- : electrical current across the series-connected capacitors C2a and C2b;
- : electrical voltage across the capacitor C2a;
- : electrical voltage across the capacitor C2b;
- : electrical voltage across diode D1;
- : electrical current flowing through the diode D1 as a function of the voltage ;
- : electrical voltage across the capacitor C4;
- : electrical current across the capacitor C4;
- : electrical current across the resistive load RL.
2.1. Characterization of Nonlinear Capacitors
The hysteresis of the electrical capacitances C2a and C2b resulting from the nonlinear properties of the ferroelectric materials was measured using the precision impedance analyzer Agilent 4294A (Agilent Technologies, Inc., Santa Clara, PA, USA, 4294A R1.11 25 March 2013) and the test fixture Agilent 16034E (Agilent Technologies, Inc., Santa Clara, PA, USA). The AC component was set to a frequency of 375 kHz with an amplitude of 5 mV and superimposed with a bias voltage varying in the range from −40 V to +40 V with a resolution of 801 points. The electrical capacitance was measured 10 times for each bias voltage and then averaged. The resulting curve of 801 points was averaged 16 times. To determine the hysteresis, the electrical capacitance of C2a and C2b was measured by varying the bias voltage from −40 V to +40 V and from +40 V to −40 V. The obtained characteristic curves of the capacitors C2a and C2b were implemented in the modeling in Mathcad and ANSYS in order to include the voltage-dependent capacitance change in the calculations (see Figure 2).
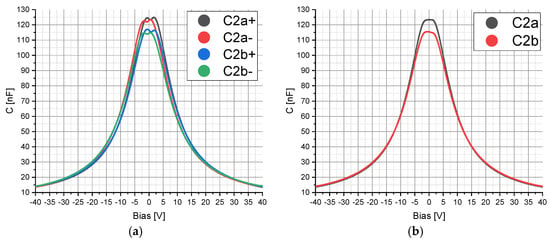
Figure 2.
Measured electrical capacitance C of the capacitors C2a and C2b (see chapter 2.1): (a) C2a₊ and C2b₊ correspond to the electrical capacitance of C2a and C2b for a change in the bias voltage from −40 V to +40 V and C2a− and C2b− correspond to the electrical capacitance of C2a and C2b for a change in the bias voltage from +40 V to −40 V; (b) curve of the averaged capacitance of C2a₊ and C2a₋ (C2a) and C2b₊ and C2b− (C2b) over the entire bias voltage range.
2.2. Modeling in Mathcad Prime 3.1
In Mathcad Prime 3.1 the circuit from Figure 1 was modeled with the first order differential Equations (1)–(10). The numerical solutions of these differential equations were calculated using the Adams, Bulirsch–Stoer, and Runge–Kutta methods of fourth order for non-stiff systems, and the Backward Differentiation Formula and Radau5 methods for stiff systems. The tolerance of the calculations was set to 10−7 and the number of points for a given solution interval was set to 50 k, 500 k, and 5 M. The step width can be constant or varying within a solution interval, depending on the solver used. The measured hysteresis of the capacitors C2a and C2b was averaged over the entire bias voltage range, then implemented in Mathcad and interpolated using third-order B-spline functions. In order to allow different modulation of the electrical capacitance of the capacitors C2a and C2b, the amplitude of the sinusoidal excitation was varied from 1 V to 30 V at a coupling factor k of 1%.
2.3. Modeling in ANSYS 2019 R2 Simplorer
In ANSYS 2019 R2 Simplorer the model is represented according to Figure 1. The solvers provided by ANSYS are based on the Euler, Adaptive Trapezoid–Euler, and Trapezoid methods. The number of points for a given solution interval was set to 50 k, 500 k, and 5 M, with a constant and adaptive step size. For an adaptive step size, the number of points for the given solution interval is determined by the solver and can vary between 50 k and 5 M. The measured hysteresis of the capacitors C2a and C2b was averaged over the entire bias voltage range and implemented in ANSYS. In order to allow different modulations of the electrical capacitance of the capacitors C2a and C2b, the amplitude of the sinusoidal excitation E1 was varied from 1 V to 30 V at a coupling factor k of 1%.
2.4. Measurement Setup for Model Validation
To validate the model in Mathcad and ANSYS, a measurement setup was realized. The components L1 and R1 (14.53 µH, 0.4 Ω, Würth Elektronik), C1 (12.45 nF, WIMA, FKP1, 2 kV), as well as L2 and R2 (3.76 µH, 0.3 Ω, Würth Elektronik) were measured with the precision impedance analyzer Agilent 4294A and the test fixture HP 1604D (Hewlett Packard, Japan). The electrical properties of the components D1 (MULTICOMP, 1N4148WS.), C4 (4.7 µF, 50 V) and RL (1 kΩ, ±1%) were taken from the datasheets. The nonlinear capacitors C2a and C2b (100 nF, +80%, −20%, Y5V, 25 V, 0608) were determined according to chapter 2.1 (see Figure 2).
Different voltages across the capacitors C2a and C2b were set by changing the distance between the inductance L1 and L2 on the primary and secondary sides. A loose coupling between the inductances L1 and L2 was ensured, so that the detuning of the resonant circuits on the primary and secondary side was avoided and a comparison between the calculations and measurements was possible. For the comparison between the modeling in Mathcad and ANSYS and the measurements, the voltage Uc2RMS, resulting from the root mean square value over time from the voltage Uc2 across the capacitors C2a and C2b, and the voltage Uc4Mean, resulting from the mean value over time from the voltage Uc4 at the load RL, were measured with the digital oscilloscope RIGOL MSO4054 (RIGOL Technologies, Inc., Suzhou, China). It should be noted that the calculations were performed on the internal memory and not on the graphical memory, otherwise the calculated root mean square would be wrong, due to insufficient resolution. The internal memory was accessed using the UltraSigma and UltraScope programs (RIGOL Technologies, Inc., Suzhou, China). The calculations refer to a measurement in a time span of 14 ms and a resolution of 700 k points. Furthermore, a pulsed inductive energy transfer at a frequency of 375 kHz, a duration of 5 ms, and a period of 1 s was performed, so that the thermal detuning of the capacitors C2a and C2b could be neglected.
3. Results and Discussion
The accuracy of the calculations using Mathcad and ANSYS was determined using Equation (11). B corresponds to the calculated and M to the measured mean value of the voltage Uc4Mean at the load. The squared difference of M and B was summed over an equal range of the root mean square voltage Uc2RMS across the capacitors C2a and C2b from 2.5 V to 26.9 V with a step width of 1 mV and subsequently divided by the number of steps N. For this calculation, M and B were interpolated piecewise linearly. The solution methods, whose results deviated strongly from the measurements, showed values of Uc2RMS outside the range of 2.5 V to 26.9 V. In this case, it should be noted that the piecewise linear interpolation in an undefined range continued to interpolate with the last known slope. As a consequence, Uc4Mean values were generated in ranges of Uc2RMS where none were originally calculated. To avoid misinterpretations, the piecewise linear interpolation was only applied to ranges of Uc2RMS in which values of Uc4Mean were calculated, values of Uc4Mean outside this range were set to 0 V. Results are shown in Table 1.

Table 1.
Deviations between the measured und calculated voltage Uc4Mean in a range of Uc2RMS from 2.5 V to 26.9 V.
The values in Table 1 indicate that for the majority of the methods used in Mathcad, with the exception of the fourth–order Runge–Kutta method with a constant step width and a number of 50 k points for the given solution interval, the calculations fit very well to the measurements with a deviation of 0.67 V. On the other hand, it should be noted that the Euler method is not suitable for modeling nonlinear properties. Good results could be obtained with the Adaptive Trapezoid–Euler method with constant step width and a resolution of 5 M points and with the Trapezoid method with a resolution of 500 k and 5 M points. However, the Trapezoid and Adaptive Trapezoid–Euler method with a resolution of 5 M points are very memory–consuming (approximately 390–444 GB).
The methods shown in Table 1 with a minimum deviation of 0.67 V provided the same time–related curve of the voltage Uc4 at the load RL. A comparison between the calculations (with a deviation of 0.67 V) and measurements is presented in Figure 3. The minimum deviation of 0.67 V is due to the fact that all components used in this measurement setup contained a certain measurement error and due to the neglect of the hysteresis losses of the capacitors C2a and C2b. A complete consistency between measurements and calculations was highly unlikely.
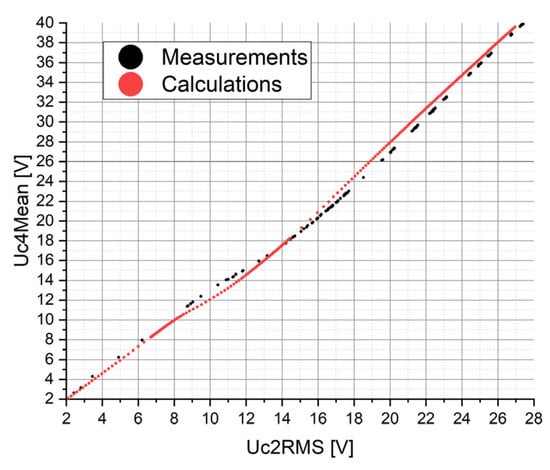
Figure 3.
Representation of the measured (black) and calculated (red) voltage Uc4Mean versus the voltage Uc2RMS.
According to Figure 3, the measured and calculated values showed the same tendency. Above a certain voltage across the capacitors C2a and C2b, the relationship between the voltages Uc4Mean and Uc2RMS changed. To illustrate this change, the voltage Uc4 at the load RL was represented for different values of Uc2RMS (see Figure 4). In the range of Uc2RMS greater than approximately 14 V, the calculated Uc4Mean values were higher than the measured values. A possible explanation for this would be that the models were based on the mean value of the hysteresis curve of the capacitors C2a and C2b and thus the associated hysteresis losses were neglected in the calculations. In other words, the threshold value to be reached by Uc2RMS for triggering the nonlinear behavior on the voltage Uc4 was lower in the calculations than in the measurements (see Figure 4). This is why the high peak of the calculated curve visible in Figure 4b occurred in the measured curve only if a higher Uc2RMS compensating the hysteresis losses was applied (Figure 4c).
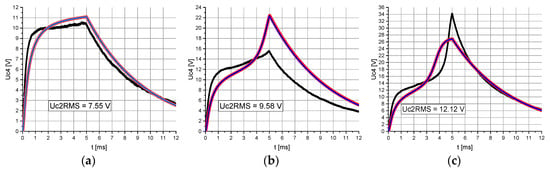
Figure 4.
Representation of the measured (black) and calculated voltage Uc4 (ANSYS, blue; Mathcad, red) at the load RL over time t. The value of Uc2RMS was stepwise increased from (a–c) by reducing the distance between the primary and secondary sides. Even for the smallest distance between primary and secondary sides (c), the resonant circuits are only weakly coupled. Representation of Uc4 for Uc2RMS equal to (a) 7.55 V; (b) 9.58 V; (c) 12.12 V.
4. Conclusions
In this paper, a model for calculating the nonlinear properties of ferroelectric materials in ceramic capacitors was presented and validated. Different solvers were used in Mathcad as well as ANSYS and compared with measured data. For the majority of the solvers available in Mathcad, except the fourth–order Runge–Kutta method with constant step width, the results were very close to the measured data with a resolution of 50 k points (deviation of 0.67 V). Furthermore, it is important to pay attention to the interpolation of the measured data of the capacitors C2a and C2b. In the case of piecewise linear interpolation, discontinuities were observed in Mathcad at certain modulation levels of the capacitors C2a and C2b, having considerable negative impact on the computing time and convergence. For this reason, B–spline functions were chosen for the interpolation of the measured data. On the basis of the calculations in ANSYS, it turned out that the Euler method was not suitable for modeling the nonlinear properties of the capacitors C2a and C2b. For the Adaptive Trapezoid–Euler and the Trapezoid method, results were obtained with the same deviation of 0.67 V at constant step width and a resolution of 5 M points as with the model in Mathcad. The same results were also achieved with the Trapezoid method with a resolution at 500 k points with constant and adaptive step size. Due to the high computing time and the memory–consuming calculations (approximately 390–444 GB) the Trapezoid method with constant step width and a resolution of 500 k points is preferable. Based on the established and validated models, the next step is to investigate a meaningful composition of nonlinear components, such as nonlinear capacitors, in order to allow an indirect sensing of the induced voltage necessary for the power supply of the implant electronics by means of a change in the nonlinear electrical capacitance. For this purpose, the current models of capacitance representation should take into account the hysteresis losses to allow a more detailed consideration of the nonlinear properties.
Author Contributions
Writing—original draft, formal analysis, investigation and methodology, Y.O.; supervision and writing—review and editing, C.M. and F.R.I.
Funding
This research was funded by the German Federal Ministry of Education and Research (BMBF, funding number 16SV7637K). The author is responsible for the content of this publication.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bloch, E.; Luo, Y.; da Cruz, L. Advances in retinal prosthesis systems. Ther. Adv. Ophthalmol. 2019, 11. [Google Scholar] [CrossRef] [PubMed]
- Mertens, A.; Raedt, R.; Gadeyne, S.; Carrette, E.; Boon, P.; Vonck, K. Recent advances in devices for vagus nerve stimulation. Expert Rev. Med. Devices 2018, 15, 527–539. [Google Scholar] [CrossRef] [PubMed]
- Wray, C.M.; Thaler, E.R. Hypoglossal nerve stimulation for obstructive sleep apnea: A review of the literature. World J. Otorhinolaryngol. Head Neck Surg. 2016, 2, 230–233. [Google Scholar] [CrossRef] [PubMed]
- Wolter, T.; Kieselbach, K. Cervical spinal cord stimulation: An analysis of 23 patients with long-term follow-up. Pain Physician 2012, 15, 203–212. [Google Scholar] [CrossRef] [PubMed]
- Doshi, P.K. Long-term surgical and hardware-related complications of deep brain stimulation. Stereotact. Funct. Neurosurg. 2011, 89, 89–95. [Google Scholar] [CrossRef] [PubMed]
- Müller, C.; Koch, T. Control Circuit for a Base Station for Transmitting Energy to a Receiver by Means of an Electric Resonant Circuit, Evaluation Device, Method and Computer Program. U.S. Patent Application No. 15/533,089, 10 May 2018. [Google Scholar]
- Seo, D.; Carmena, J.M.; Rabaey, J.M.; Alon, E.; Maharbiz, M.M. Neural Dust: An Ultrasonic, Low Power Solution for Chronic Brain-Machine Interfaces. 2013. Available online: http://arxiv.org/pdf/1307.2196v1 (accessed on 14 November 2019).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).