Evaluating Temperature Influence on Low-Cost Piezoelectric Transducer Response for 3D Printing Process Monitoring ^†

Abstract

The 3D printing process deals with the production of three-dimensional objects with defined geometries. However, this manufacturing process has a crucial point established at the beginning of the object manufacturing, where anomalies can occur and compromise the entire object produced. The piezoelectric diaphragm has been studied as an alternative to the conventional acoustic emission (AE) sensor concerning the monitoring of structures and processes. It has in its assembling a ceramic element with piezoelectric properties, which makes its response sensitive to temperature variations. The Pencil Lead Break (PLB) method is widely used due to its efficiency in the characterization of AE sensors. The present work aims to study the influence of temperature on the piezoelectric diaphragm response for the monitoring of the 3D printing process. PLB tests were performed on the glass surface of a 3D printer at three different temperatures, and the raw signal was collected at 5 MHz sample rate. The signal was investigated in the time and frequency domain. The results demonstrate that the frequency response of the sensor is directly influenced by the temperature variations. In addition, the signal amplitude variations occur differently along the entire spectrum, and frequency bands with small and large amplitude variations can be selected for a comparison study. Furthermore, two frequency bands were carefully selected, and the mean error was obtained regarding the reference temperatures of 25 and 45 °C. It can be inferred that the piezoelectric transducer has low sensitivity to temperature variation if a proper frequency band is selected, where an acceptable error of 16.9% was obtained.

1. Introduction

The 3D printing process, a term commonly assigned to the Fused Deposition Modeling (FDM) technology, has been widely used to manufacture components and parts for numerous applications [1]. The quality of the part obtained by the 3D printing process is directly related to the software chosen for the process control, as well as its parameters, such as the printing table temperature and the extruder temperature, which, if incorrectly set, can cause the failure of the components produced [2]. Different manufacturing processes, including the 3D printing process, can be monitored to ensure the quality of the fabricated parts.

The usage of sensors, allied with the digital signal processing to monitor the additive manufacturing processes, can be found in a large number of applications. For instance, acoustic emission (AE) sensors are applied in the monitoring of Selective Laser Melting (SLM) [3], Laser Metal Deposition (LMD) [4] and FDM manufacturing processes [2,5], as well as accelerometers are used for monitoring of the FDM process [6].

The piezoelectric diaphragm fabricated using lead zirconate titanate (PZT), commonly referred to as a buzzer, has in its assembling a ceramic element with piezoelectric properties, which is responsible for generating an electrical voltage in response to an applied force or pressure. The function of the sensor constituted of piezoelectric materials is to detect the mechanical changes that occur in the structures and to convert them into electrical signals. Due to the importance of these sensors, the study of their frequency response under various process conditions, such as temperature changes, is very important. Sensors submitted to different temperatures perform different frequency responses, resulting in errors in the measurements made by the sensors, which may discredit the monitoring and control of the process. The piezoelectric diaphragm has been studied as an alternative to the acoustic emission sensor due to its reduced cost [7].

Due to the importance of piezoelectric sensors in the monitoring of manufacturing processes, it is essential that they are properly evaluated for their application. Some methods that verify the response of these sensors can be found in the literature, and among them, the Pencil Lead Break (PLB) stands out [8]. The PLB is a standardized method settled as a replicable artificial source of acoustic emission [9]. Using a mechanical pencil, the graphite tip is firmly pressed against the surface of interest until breakage. At this moment, the stored stress is quickly released, generating microscopic movements on the surface of the structure and releasing acoustic waves that propagate through the analyzed structure. The fast release of these waves acts as a pulse, enabling the frequency response of the sensor to be measured.

Monitoring manufacturing processes through sensors such as acoustic emission is a widely used practice nowadays. However, the reduced cost of piezoelectric diaphragms is captivating compared to those of traditional AE sensors. Therefore, the present work proposes the study of the influence of temperature on the piezoelectric diaphragm for the monitoring of the 3D printing process, in which the PLB method is used in the printing table and the digital signal is processed. A better understanding of this piezoelectric diaphragm frequency response allows its use in monitoring the 3D printing process, as an alternative to AE sensors.

2. Materials and Methods

2.1. Experimental Setup

The present work is based on experimental procedures to investigate the influence of temperature variation on piezoelectric diaphragm response in 3D printing process monitoring. The tests were performed in a desktop 3D printer, manufacturer GTMax, model Graber i3. This model has a heated MK2B Dual Power PCB table with NTC 100k thermistor type temperature sensor, which is in contact with a glass panel with the dimensions 200 × 200 × 3 mm. In addition, a piezoelectric diaphragm of 20 mm diameter and 0.42 mm thickness was fixed to the table through multiple layers of a silicon-based adhesive at a distance of 14 and 100 mm from the lower right corner of the table. An oscillograph, model DL850, from Yokogawa, was used for data collection and storage. Lastly, the graphite used in the PLB method had a 2H hardness and measured 0.5 mm in diameter. The graphite length and the mechanical pencil angle were established in accordance with ASTM E976.

The temperature control of the glass table, in which the PZT was mounted, was performed by the printer heating system and controlled through Repetier-Host^® software. The ambient temperature of 25 °C was considered as baseline. In the tests, five pencil lead breaks were performed for each selected temperature: 25, 45, and 65 °C, maintaining a 45° angle between the graphite and the table. The oscillograph stored the acoustic signals, collected at a sampling rate of 5 MHz, and the data were later digitally processed with Matlab^® software.

2.2. Signal Processing

A previous study was conducted on the frequency spectrum of a 3D print signal. It has been observed that frequency spectrum amplitudes decay much beyond the 800 Hz range, blending with process noise, compatible with the results obtained by Tlegenov et al. [6].

The raw signals obtained were analyzed in both time and frequency domains. The average frequency spectrum was calculated from the five signals obtained for each temperature. From the averaged frequency spectrum signal, an amplitude variation study was conducted similarly to the one used by Ribeiro et al. [7]. Then, observing the spectrum up to 800 Hz, frequency bands with larger and smaller amplitude variations relative to those at the baseline temperature were chosen. From the spectral curves of each band, the mean error was used as a parameter to better analyze the influence of temperature on the signals obtained by the piezoelectric diaphragm. Equation (1) presents the calculation of the average error used.

$$\mathrm{error}(\%)=[{\displaystyle \sum }_{{\mathrm{k}=\mathrm{f}}_1}^{{\mathrm{f}}_2}(\frac{{\mathrm{S}}_{\mathrm{a}}\left(\mathrm{k}\right){-\mathrm{S}}_{\mathrm{b}}\left(\mathrm{k}\right)}{{\mathrm{S}}_{\mathrm{b}}\left(\mathrm{k}\right)}{*100\left)\right]/(\mathrm{f}}_2{-\mathrm{f}}_1+1)$$

(1)

where S_a is the signal obtained at a temperature other than the baseline, S_b is the signal obtained at the reference temperature (baseline), k the frequency at which the signals were analyzed, f₂ the upper limit of the analyzed frequency range, and f₁ the lower limit of frequency range analyzed.

The mean error calculation was performed in the signal spectra from temperature variations of 45 and 65 °C in relation to the baseline, for different frequency bands. These temperatures were chosen because they are within the range utilized for the material and printer used in this work.

3. Results and Discussion

3.1. Frequency Spectrum Analysis

As described in Baptista et al. [10], there are differences in phase change and amplitude as a function of frequency for signals obtained at different temperatures by the electromechanical impedance (EMI) technique for the PZT sensor. Nonetheless, the basic constitution of PZT and AE sensors is similar, for the reason that both use a piezoelectric material in their structure and rely upon mechanical changes in the material under analysis to obtain their respective responses. 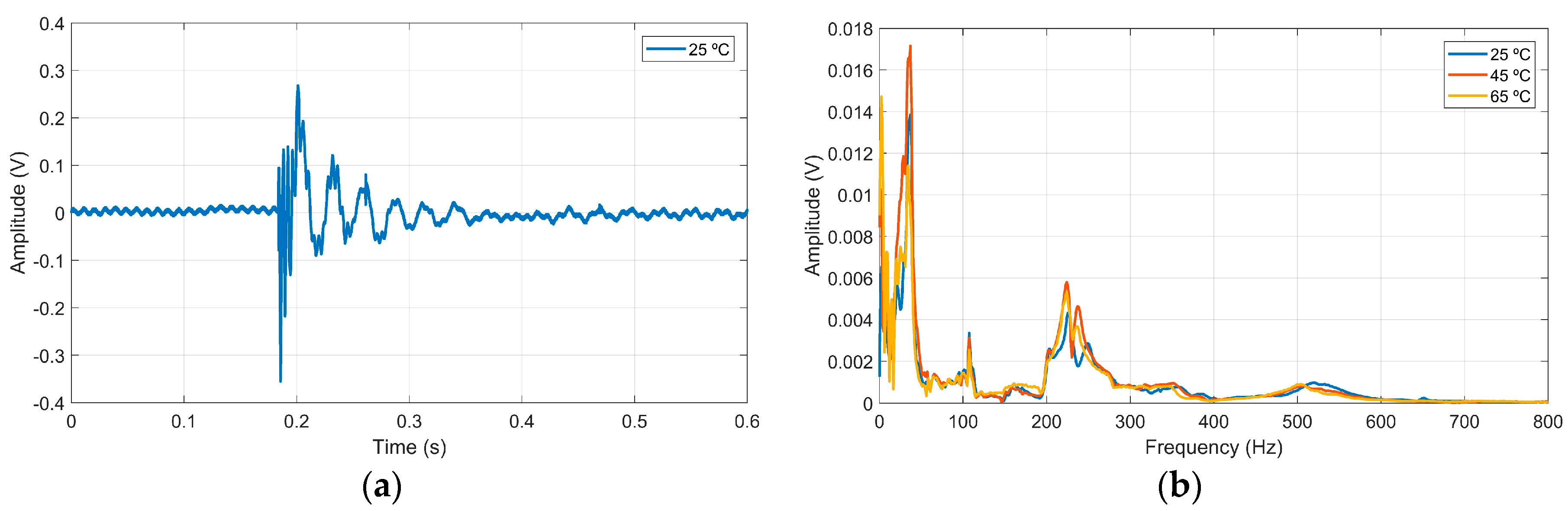One of the signals obtained by the PLB test on the printing table can be seen in Figure 1a, and the mean frequency spectrum of the PLB signal for the three temperatures under study can be seen in Figure 1b.

Figure 1a shows the transducer response to the mechanical impulse produced by the graphite breakage on the printer table. The Z transform of this signal is approximately the transfer function of the transducer, since the time convolution of the transducer transfer function and the input pulse signal constitute the transducer transfer function itself. Figure 1b shows the response signal spectrum, where it is perceived that for the 200 to 300 Hz frequency range the signal amplitudes were generally higher at 45 and 65 °C, except for a small range near 280 Hz. However, for frequencies in the range of 500 and 600 Hz, the signal amplitudes for the temperature of 25 °C were higher, after this point, the curves overlapped. Therefore, it is perceived that temperature significantly influences the signal response of the piezoelectric transducer.

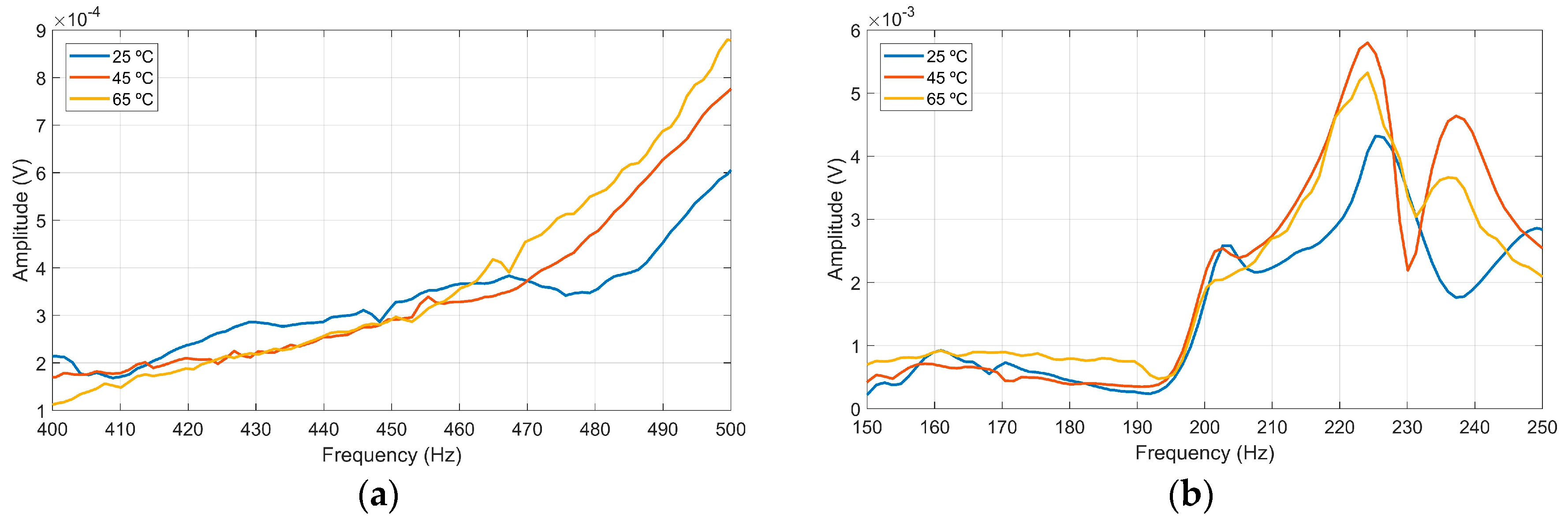
The amplifications of the frequency bands selected for this study can be observed in Figure 2. It is noted that the frequency band presented in Figure 2a had several overlap zones, indicating low sensitivity changes in temperatures. Nevertheless, the band presented in Figure 2b had quite different behavior, in other words, a greater sensitivity to temperature variations was observed.

3.2. Mean Error Assesment

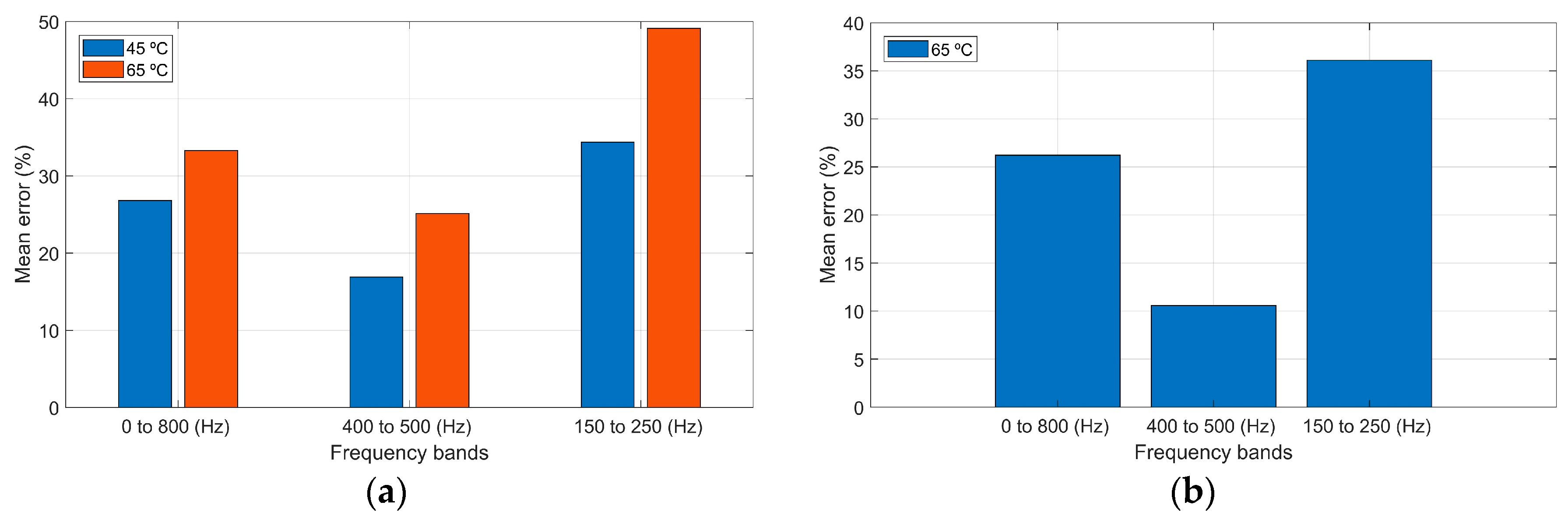
After band selection, the mean error between the 45 and 65 °C temperature signals in relation to the baseline of 25 °C was calculated. The average errors calculated for the selected frequency bands, as well as for the entire observed spectrum, are presented in Figure 3a. The frequency band with the highest quantity of overlap zones, that is, 400 to 500 Hz, presented the smallest errors, where values of 16.9% at 45 °C and 25.2% at 65 °C were found. The frequency band with the least overlap, that is, 150 to 250 Hz, presented the biggest errors, where values of 34.4% at 45 °C and 49.1% at 65 °C were found. When calculating the mean error in relation to the baseline for the entire observed frequency spectrum, the average errors of 26.8% for the 45 °C temperature and 33.3% for the 65 °C temperature were obtained.

On the other hand, Figure 3b shows the mean error between the signal at 65 °C and the baseline signal at 45 °C. The frequency band of 400 to 500 Hz, which has the highest quantity of overlap zones, presented an error of 10.6%. The frequency band with the least overlaps, that is, 150 to 250 Hz, presented an error of 36.1%. When calculating the mean error in relation to the baseline for the entire observed frequency spectrum, the average error of 26.2% was found.

Therefore, it can be inferred that the influence of temperature on the response of the piezoelectric diaphragm, established by the expansion of the piezoelectric element and characterized by the increase in mean error, varies over the entire frequency range of the transducer. It is therefore of extreme importance to know the errors involved in the spectrum amplitudes of the piezoelectric transducer due to the temperature influence, either for process monitoring using the full signal spectrum or for a specific frequency range selected for study.

4. Conclusions

Time-domain signals of a low-cost piezoelectric diaphragm were acquired by the PLB method to investigate the effect of temperature on these signals for monitoring the 3D printing process. From the signals collected from the sensor fixed to the printing table, its spectrum was extracted for different table temperatures. Based on the frequency spectrum, two frequency bands were carefully selected to study the errors involved at temperatures of 45 and 65 °C relating to the baseline temperature of 25 °C, and also the temperature of 65 °C relating to the baseline temperature of 45 °C. It was noted that the selected band from 400 to 500 Hz, which had the largest overlap of the spectra, presented the smallest errors, being 16.9% at 45 °C and 25.2% at 65 °C. At the same time, when comparing the errors of this band, 400 to 500 Hz, with those of the whole spectrum, from 0 to 800 Hz, an amplitude error for this band of approximately 1.6 times smaller is obtained at a temperature of 45 °C and 1.3 times lower at 65 °C, which are much smaller than those of the other selected band. Finally, the comparison of the errors between the temperatures of 65 and 45 °C revealed that the behavior of the errors is similar, although the errors are smaller, as expected, due to smaller temperature differences.

In conclusion, the temperature significantly influences the signal amplitudes of the low-cost piezoelectric transducer to monitor the 3D printing process. This influence might be very large for certain frequency bands, as demonstrated in the present study, because the amplitude differences are very large in relation to the ambient temperature normally used as a baseline for these sensors in various manufacturing processes. However, for the 3D printing process, the table temperature is usually higher than the ambient temperature, while the correction of signal amplitude errors due to temperature must be in relation to a minimum temperature value, specified by the printer manufacturer, which in this work was considered as 45 °C. Additionally, it has been shown that the influence of temperature can be much smaller for a given frequency band than for the entire spectrum, which in this case was due to the large overlap of the spectra in the selected frequency band.