Polysilicon MEMS Sensors: Sensitivity to Sub-Micron Imperfections ^†

Abstract

In this work, through Monte Carlo analyses on statistical volume elements, we show the effect of the grain morphology and orientation on the effective elastic properties of polysilicon beams constituting critical MEMS components. The outcomes of the numerical investigation are summarized through statistical (lognormal) distributions for the elastic properties as functions of grain size and morphology, quantifying therefore not only the relevant expected mean values, but also the scattering around them. Such statistical distributions represent a simple, yet rigorous alternative to cumbersome numerical analyses. Their utility is testified through the analysis of a statically indeterminate MEMS structure, quantifying the possible initial offset away from the designed configuration due to the residual stresses arising from the micro-fabrication process.

1. Introduction

The drive towards miniaturization in the MEMS industry leads unavoidably to questions of homogeneity, which is commonly accepted from the continuum mechanics perspective. For polysilicon films, grain morphology and orientation eventually influence the mechanical response of MEMS devices when critical structural components (such as the suspension springs) are downsized [1,2,3,4,5,6]. Moreover, the deep reactive-ion etching process, leading to so-called over-etch [7] whose relevance gets increased when referred to dimensions comparable with the grain size, affects the accuracy of the geometrical layout [8]. Under these conditions, the expected spread in the operational behavior of the devices is a matter of concern both for MEMS design and reliability [9,10]. While this consequence is well known and expected, the quantification of the aforementioned spread is far from being under control.

In this work, we focus on the analysis of the shift from the designed position for a statically indeterminate MEMS structure subject to residual stresses arising from the production process. While in an ideal design the exact dimensions and elastic behavior of the structural components can be foreseen with reasonable accuracy, in practice the dimensions of critical components become comparable with the silicon grain size. Accordingly, the material should be handled as heterogeneous, and the movable structure as an uncertain domain. Even if the effects of the scattering around the target elastic properties on the overall MEMS behavior are shadowed by other issues, for a moving mass held into position by nominally identical springs, the uncertainty about the stiffness properties immediately leads to a sensible offset away from the reference. This offset comes into play because of the always-present residual stresses in the polycrystalline silicon film, as shown in the next (Section 2). To account for the intrinsic stochastic nature of the problem, we propose in Section 3 to artificially build, via Voronoi tessellations, stochastic volume elements (SVEs) whose size is related to the MEMS’ critical component size. Each realization of the SVEs includes its own silicon grain morphology, so that accurate finite element (FE) analyses can provide the cumulative distribution function (CDF) of the relevant elastic properties. To overcome the computational burden in the analysis at the MEMS level, the numerical CDFs are best fitted with lognormal distributions. By means of these latter analytical CDFs, in Section 4 we show how to estimate the overall stiffness of (even folded) beams and how to apply such estimates to the quantification of the offset induced by the residual stresses.

2. Statically Indeterminate MEMS Structure

We consider a rather simple scheme, common to several MEMS devices [11]: a movable plate, of mass m, is connected to the substrate via two suspension springs. Even if nominally identical as discussed in the Introduction, we assume that the stiffness is a stochastic variable, so that the values relevant to the two springs are k₁ = k + ∆₁ and k₂ = k + ∆₂, k being the target and ∆₁ ≠ ∆₂, (either positive or negative) being the two values drawn from the CDF. The source of this difference is here assumed to be due to the effect of the morphology only; spatially-varying over-etch defects are therefore disregarded.

As the microstructure is statically indeterminate, an internal force F, to be considered the resultant of the residual stresses, provides a displacement of the movable mass whenever k₁ ≠ k₂. The relationship between this force and the offset displacement u away from the rest condition reads:

$$u=\frac{{∆}_1-{∆}_2}{2\left(k+{∆}_1\right)\left(k+{∆}_2\right)}F$$

(1)

where the sensitivity to the imperfections ∆₁ and ∆₂ of the spring stiffness is evidenced.

In the proposed framework, each quantity in Equation (1) is a random variable.

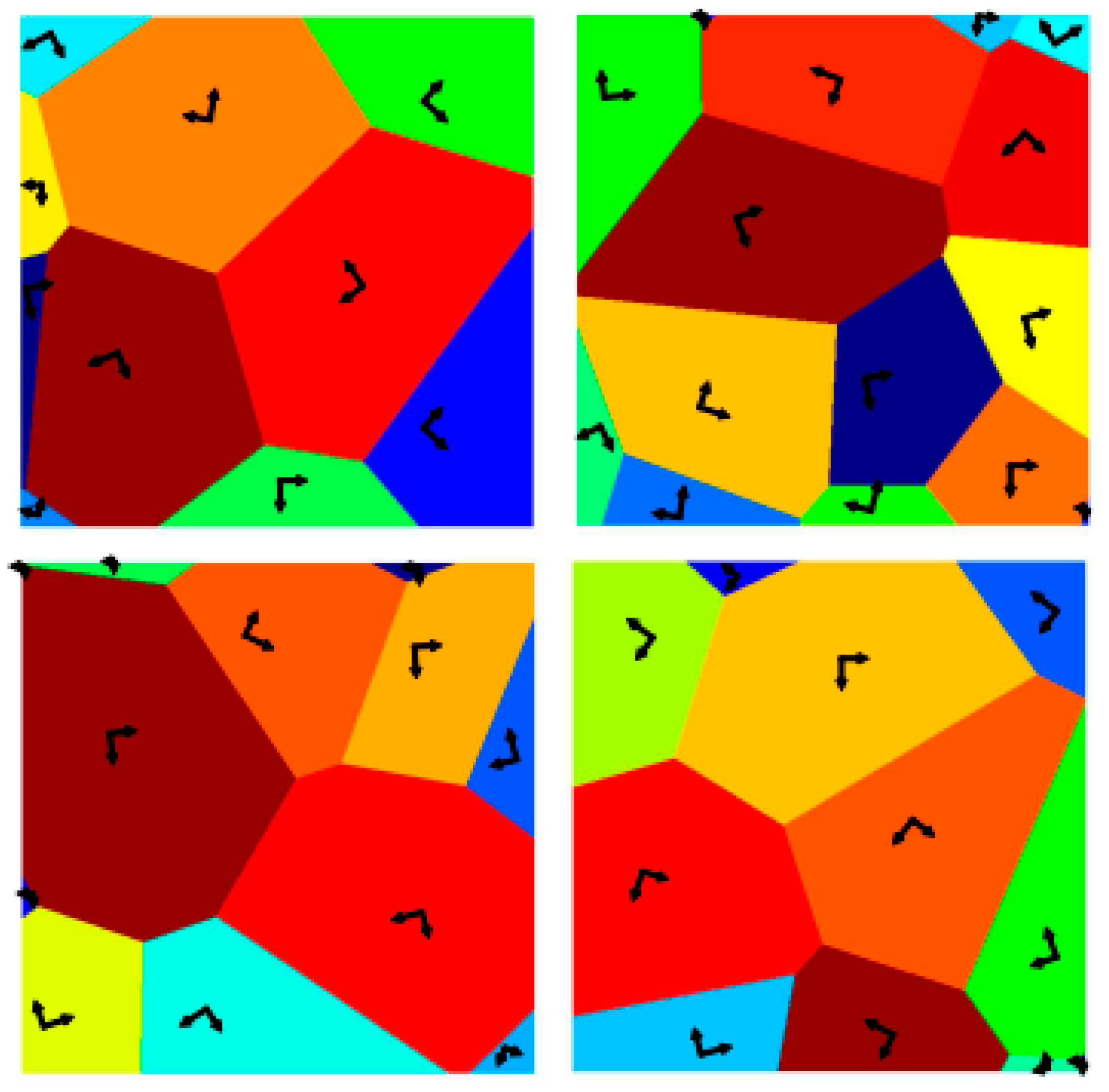
3. Spring Stiffness as a Function of Polysilicon Grain Morphology

To account for the influence of film morphology on the spring stiffness, we adopt numerical simulations exploiting an artificial Voronoi tessellation to build the polycrystalline grain boundary network [12]. The whole spring should be subdivided into silicon grains, each one owning its own axes of elasticity. As the numerical costs of such an approach would be significantly high and the result would be valid for a specific spring geometry only, we introduce a square SVE, whose dimensions are equal to the spring nominal width. Two geometries are here handled, of size 2 × 2 μm² and 3 × 3 μm² (see Figure 1). At variance with the analyses of representative volume elements (RVEs) [13,14], where an averaged value only is obtained for the elastic properties, with SVEs an estimate of the probability distribution of the mentioned properties is obtained [15]. Therefore, by carrying out the homogenization of the SVE elastic properties in a Monte Carlo analysis, we obtain the CDF for these quantities: in Figure 2, for the two SVE cases 2 × 2 μm² and 3 × 3 μm², the CDFs of the in-plane Young’s modulus are depicted. The FE analyses are run by applying two different types of boundary conditions (BCs), i.e., by applying a uniform stress (labelled “E-force” in the figure) or a uniform strain (labelled “E-disp” in the figure) BCs to bound the real results [12]. As is well known in the relevant literature [13], the plots in Figure 2 show that the uniform strain BCs provide an upper bound (orange line), while the uniform stress BCs provides a lower bound (red line) on the actual solution. By comparing the graphs for the two SVE sizes, it is clear that the 3 × 3 μm² SVE is characterized by values closer to the mean, with a steeper distribution around it. The greater variability of the 2 × 2 μm² SVE is expected, since in this latter case the grain size becomes comparable with the SVE dimension.

Each numerical CDF is then fitted with a lognormal distribution

$$L_E\left(x\right)=\frac{1}{2}+\frac{1}{2}\mathrm{e}\mathrm{r}\mathrm{f}\left[\frac{\ln x-\mu }{\sqrt{2}\omega }\right]$$

(2)

where x is the random variable representing the Young’s modulus as an output of the SVE analyses, erf[·] is the Gauss error function, and μ and $\omega$² are the mean and the variance to be evaluated.

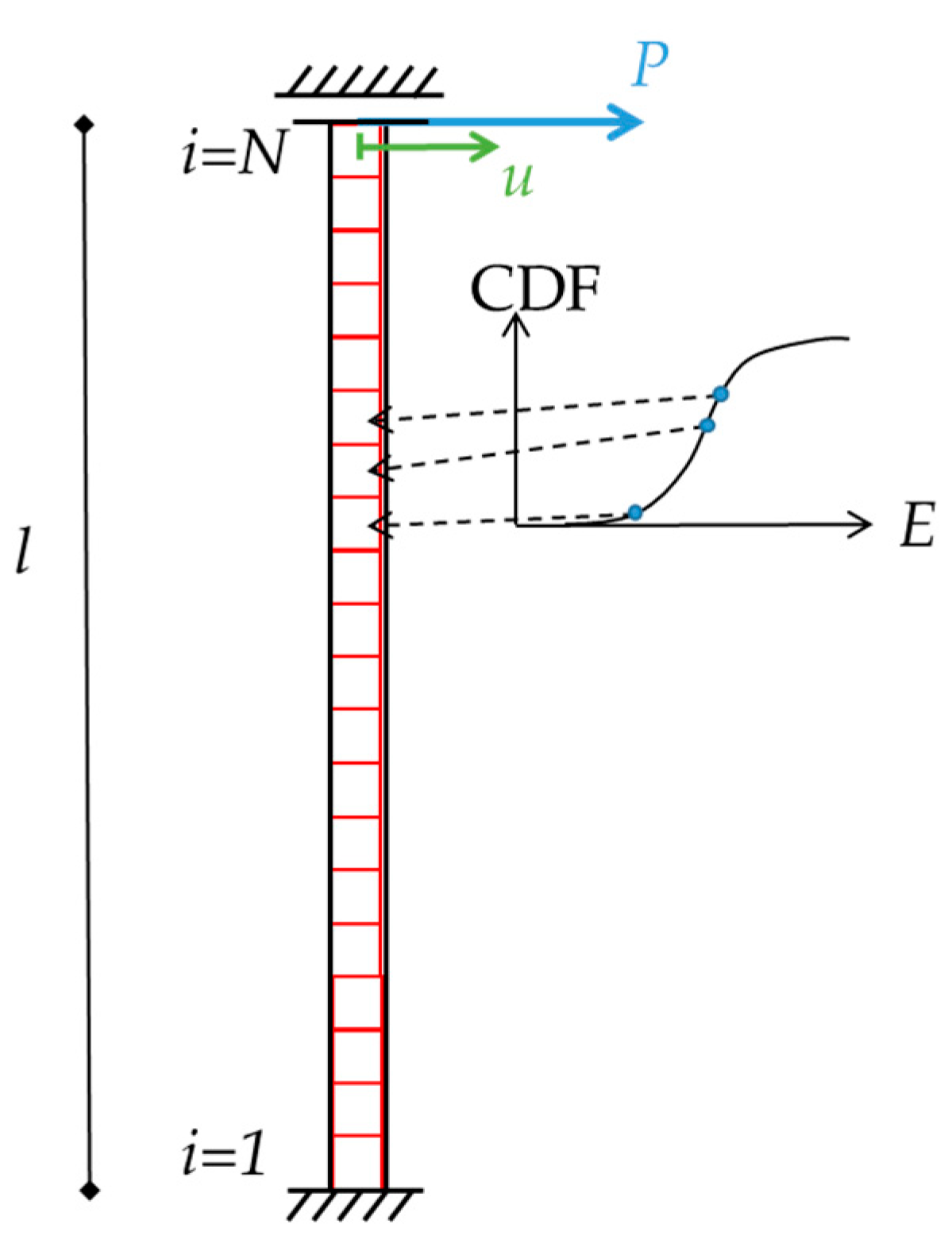
4. Estimate of the Overall Spring Stiffness

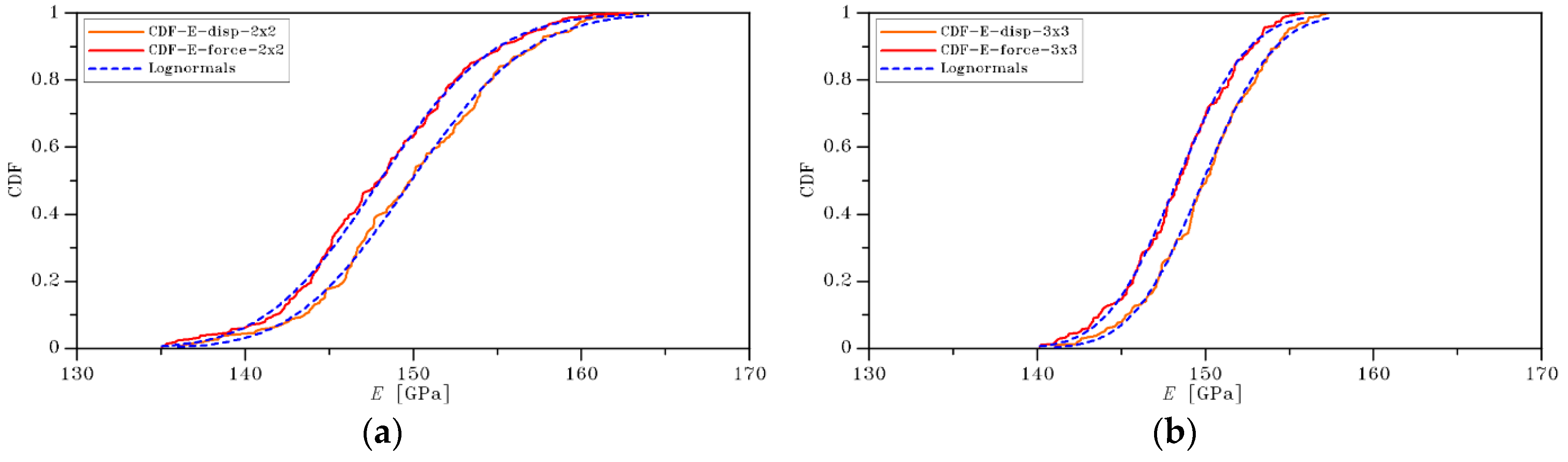
4.1. Methodology

Once the lognormal CDFs have been set for the SVE, the geometry of a suspension spring can be subdivided into subsets, whose geometry is related to the SVEs dimensions, see Figure 3. We postulate that the overall stiffness is obtained by assigning to each subset a Young’s modulus extracted from the corresponding CDF.

We consider here a simple beam geometry, with a fixed constraint at one end (no displacements and no rotations allowed) and a slider at the opposite end, where the motion is in the direction perpendicular to the beam axis only, while no rotations are allowed. By means of the principle of virtual work, and allowing for beam slenderness to neglect shear strains, the force P and the corresponding displacement u can be related to provide the ratio P/u as the beam stiffness k.

The outcomes of this reasoning, that depends on the number of subdivisions N along the beam length, is:

$$k=\frac{P}{u}=\frac{I}{l^3}\left(\frac{1}{\sum _{i=1}^N\frac{{\psi }_i}{E_i}}\right)$$

(3)

where: i is the index running over the subsets handled; ${\psi }_i$ is a corrective factor dependent on the placement of the i-th subset; I is the moment of inertia of the beam, and $l$ is the beam length (assumed here equal to 200 μm or 300 μm in the analyses). Since the overall stiffness is a function of the random variable E, then it is a random variable too.

The actual CDF of F resulting from the production process can be estimated as well. Without any specific reference to real conditions, in this work we assume for F a normal distribution with a mean value of 10 MPa and a variance of 1.667 MPa.

4.2. Discussion

In Figure 4, the CDFs of the offset of the mass from the rest condition are reported, as obtained with Monte Carlo analyses based on Equation (1). In orange we show the CDFs obtained with the (analytical) lognormal distributions, while in black we provide the CDFs obtained from the SVE-finite element simulations. Since the mean value is the same (zero offset), the main difference between the two solutions is mostly due to the correct approximation of the variance of E, and therefore, of k. The analytical approach, which is less expensive with respect to the computational one, represents correctly the information obtained from the FE analyses, where the microstructure has been taken into account through the SVEs. Around the zero-mean value, the offset becomes positive or negative depending on the difference between the stiffnesses of the right and left springs. The 200 × 2 case (beam length equal to 200 μm, width equal to 2 μm) actually shows a larger variability of the offset with respect to the 300 × 3 case, as expected from the larger spread in the lognormal CDF shown in Figure 2a with respect to Figure 2b.

It is worth emphasizing that the offset is generated by the scattering of the values of the spring stiffnesses around the mean: therefore, it depends on the standard deviations of the CDFs, and not on the mean values. Any stochastic method providing an offset estimate should then address the quantification of the variance of the random variables associated to the elastic properties, not only of their mean values.

5. Conclusions

In this work, we have proposed a method to estimate the offset from the rest position of statically indeterminate structures of MEMS devices, featuring a moving mass held into position by two springs. Because of the uncertainties of the microfabrication process, a stochastic Monte Carlo method has been adopted to account for the heterogeneity of the material in addressing the definition of the elastic properties. The polycrystalline morphology has been accounted for by a Voronoi tessellation of statistical representative volumes, whose dimensions have been assumed equal to the spring width, comparable with the silicon grain size.

The homogenized Young’s modulus, obtained with the finite element simulations, has provided a numerical cumulative distribution function that has been approximated by an analytical, lognormal distribution for each SVE size. These analytical distribution functions have been then used to describe the stiffness of a spring supporting the moving mass. In the presence of residual stresses, an internal force, to be considered as the relevant resultant and treated as a normally-distributed random variable, provides an offset from the rest position. Such an offset is actually found to depend on the variance of the stochastic Young’s modulus of the SVE, and not on its mean value.