Abstract
The development of new low-cost transducers and systems has been extensively aimed at in both industry and academia to promote a correct failure diagnosis in aerospace, naval, and civil structures. In this context, structural health monitoring (SHM) engineering is focused on promoting human safety and a reduction in the maintenance costs of these components. Traditionally, SHM aims to detect structural damages at the initial stage, before it reaches a critical level of severity. Numerous approaches for damage identification and location have been proposed in the literature. One of the most common damage location techniques is based on acoustic waves triangulation, which stands out as an effective approach. This method uses a piezoelectric transducer as a sensor to capture acoustic waves emitted by cracks or other damage. Basically, the damage location is defined by calculating the difference in the time of arrival (TOA) of the signals. Although it may be simple, the detection of TOA requires complex statistical and signal processing techniques. Based on this issue, this work proposes the evaluation of a low-cost piezoelectric transducer to determine damage location in metallic structures by comparing two methodologies of TOA identification, the Hinkley criterion and the statistical Akaike criterion. The tests were conducted on an aluminum beam in which two piezoelectric transducers were attached at each end. The damage was simulated by pencil lead break (PLB) test applied at four different points of the specimen and the acoustic signals emitted by the damage were acquired and processed by Hinkley and Akaike criteria. The results indicate that, although both signal processing methodologies were able to determine the damage location, Akaike presented higher precision when compared to Hinkley approach. Moreover, the experimental results indicated that the low-cost piezoelectric sensors have a great potential to be applied in the location of structural failures.
1. Introduction
Non-destructive testing (NDT) methods applied in structural health monitoring (SHM) systems have been extensively studied to develop low-cost transducers and systems aiming to promote the correct failure diagnosis and damage location in aerospace, naval, and civil structures [1,2,3]. Traditionally, SHM aims to detect structural damages at the initial stage, before it reaches a critical level of severity, ensuring human safety and reducing maintenance costs. In this context, numerous approaches for damage detection and location have been proposed in literature [1,2]. One of the most promising damage location techniques is based on the triangulation of acoustic waves (AE) [2,4,5,6,7]. Basically, a set of piezoelectric transducers is attached on a host structure in order to capture the acoustic waves produced by failures or cracks. In this approach, the damage location is determined by a mathematical model that uses the difference of the time of arrival (TOA) of the signals and the wave velocity propagation in the component [4,5,6,7]. Although this method may be simple, the detection of TOA requires complex statistical and signal processing techniques. Based on this, this work presented a comparative study between the application of Akaike and Hinkley criteria for TOA determination [6,7,8,9] using low-cost piezoelectric diaphragms.
The outline of this article is as follows: Section 2 presents the basics concepts of piezoelectric transducers, and Section 3 presents the signal processing triangulation by applying statistical criteria, i.e., the Akaike and Hinkley criteria. The experimental setup is described in Section 4, and the results are discussed in Section 5. The conclusion of this paper is presented in Section 6.
2. Piezoelectric Transducers and AE Damage Detection
The piezoelectric effect is the behavior of special materials in which an electrical voltage is generated resulting from a mechanical stress (direct effect) and vice-versa (reverse effect). Therefore, piezoelectric transductors can work as both sensors or actuators. The basic constitutive relations of the direct and reverse piezoelectric effects for piezoelectric materials are given by Equations (1) and (2), respectively [10]:
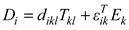
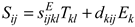 where dikl and dkij are piezoelectric constants; Sij is the mechanical strain component; Tkl is the mechanical stress component,
where dikl and dkij are piezoelectric constants; Sij is the mechanical strain component; Tkl is the mechanical stress component, 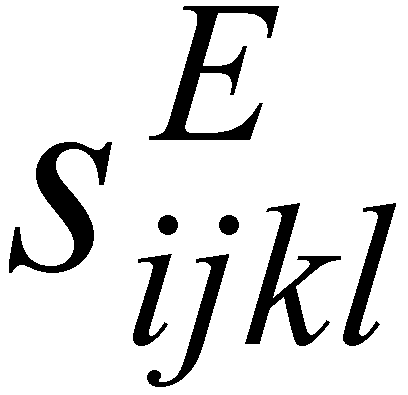 is the elastic compliance under a constant electric field, Ek and Di are the electric field and electrical displacement components, respectively,
is the elastic compliance under a constant electric field, Ek and Di are the electric field and electrical displacement components, respectively, 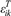 is the permittivity component at a constant stress, and the subscripts i,j,k,l represent the natural coordinate system of the piezoelectric crystal and take values of 1, 2 or 3.
is the permittivity component at a constant stress, and the subscripts i,j,k,l represent the natural coordinate system of the piezoelectric crystal and take values of 1, 2 or 3.
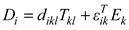
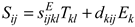
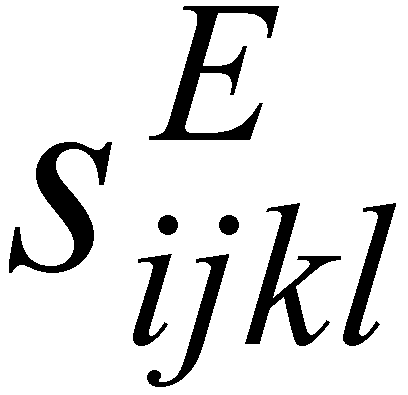 is the elastic compliance under a constant electric field, Ek and Di are the electric field and electrical displacement components, respectively,
is the elastic compliance under a constant electric field, Ek and Di are the electric field and electrical displacement components, respectively, 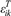 is the permittivity component at a constant stress, and the subscripts i,j,k,l represent the natural coordinate system of the piezoelectric crystal and take values of 1, 2 or 3.
is the permittivity component at a constant stress, and the subscripts i,j,k,l represent the natural coordinate system of the piezoelectric crystal and take values of 1, 2 or 3.Due to the direct piezoelectric effect shown in Equations (1) and (2), this kind of transductor can be set as an acoustic emission (AE) sensor because waves generate mechanical stress and therefore electrical voltage. One application of this sensor is the location of failures in metallic structures. Material delamination, breakage, impacts, shear, friction, or any kind of physical-chemical damage would generate ultrasonic waves [2,3,4,5], and therefore could be located using such sensors. For example, damage in metallic materials generates acoustic waves between 20 and 500 kHz, which is easily detectable by this kind of sensor. The transducers used in this work were the piezoelectric diaphragms, which have similar characteristics to conventional lead zirconate titanate (PZT) ceramics [11,12]. The piezoelectric diaphragms consist of a circular brass plate, with dimensions of 35 × 0.2 mm, and a circular piezoelectric ceramic, with dimensions of 23 × 0.22 mm and an attenuation of 3 dB at 225 kHz [9].
3. Triangulation Concept for Electric Signals and TOA Algorithms
The triangulation concept is usually applied with damage location methodology using acoustic emission waves. This concept measures the wave travelling time using a set of different located sensors assembled into a damaged structure. Damage, e.g., a crack, generates an acoustic wave that travels within the structure, and the distances between the damage and the different sensors are measured, locating the damage. The first sensor (Sl) is called the reference sensor, n is the number of sensors in the structure, and the excitation time is the time acquired by the sensors (Tsn), as shown in Figure 1. Thus, for the current system, there are ‘n – 1′ measured travelling time differences (Δti). Based on the wave propagation velocity in the structure and on sensor position coordinates (xsi,ysi,zsi), spherical equations can be solved to obtain damage origin coordinates (x,y,z) [5,6,7].
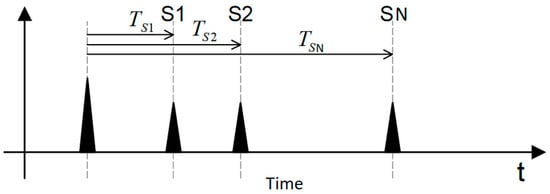
Figure 1.
Schematic visualization of acoustic arrival times on a set of sensors (S1, S2, …, SN) [7].
As the time differences (Δti) are known, the number of unknown variables is the same as the number of equations. Thus, for each sensor i, for 1 < i < n, the mathematical model generated from triangulation concept is given by
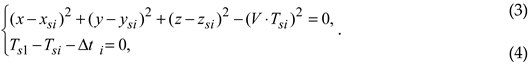
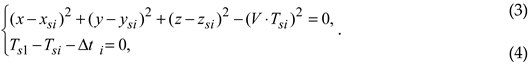
In order to precisely determine the TOA of an acoustic wave, it is necessary to use robust algorithms to process the electrical signals and to calculate the Δti. Akaike and Hinkley criteria are widely used to determine TOA and process signals.
The Hinkley Criterion (HC) and the Akaike Information Criterion (AIC)
The Hinkley criterion (HC) and the Akaike information criterion (AIC) are algorithms used for acoustic wave characterization in which energy and frequency values can vary within a wide range. Both are complex algorithms and can detect changes in wave signal in time, which make them suitable for TOA detection arising from acoustic and seismic waves. Both approaches consider the signals as autoregressive processes in which each sample is a linear combination of past values [7,8,9]. The Hinkley curve of a signal y[n] is defined as the cumulative sum of all amplitude values, as shown by Equation (5):
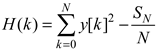 where SN and N are the global energy and the total number of signal samples, respectively. The global minimum value found in the Hinkley curve is the starting time, i.e., the time in which a sensor is initially activated by ultrasound waves. On the other hand, the Akaike criterion calculates TOA based on the local minimum value at the AIC curve [6,7], as follows:
where SN and N are the global energy and the total number of signal samples, respectively. The global minimum value found in the Hinkley curve is the starting time, i.e., the time in which a sensor is initially activated by ultrasound waves. On the other hand, the Akaike criterion calculates TOA based on the local minimum value at the AIC curve [6,7], as follows:
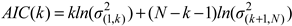 where σ2 is the variance, and N is a number of y[n] samples.
where σ2 is the variance, and N is a number of y[n] samples.
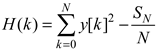
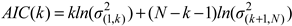
4. Experimental Setup
Two piezoelectric diaphragms (PZT1 and PZT2) were positioned, one in each end, on an aluminum beam (2.5 m × 0.075 m × 0.003 m) using cyanoacrylate glue. Thick layers of foam were placed under the beam to avoid external vibration or signal interference. Damages on the surface were created in four different locations on the beam’s surface using the pencil lead break (PLB) test. The experiment was conducted following the E976-10 guideline, which uses a displacement of mass to generate acoustic waves [13]. In other words, a mechanical pencil is pushed against a material until the breakage of the graphite. The pushing generates an instantaneous damage and, as a consequence, a microscopic displacement of mass [13]. In this study, four PLB tests were generated in four different points (x; y) on the beam surface: (0.5; 0.038), (1.25; 0.038), (0.5; 0.038), and (2.5; 0.038) meters. As the aim of this study is to compare the precision of both methods, variation in the y direction was not performed. After each pushing, the TOA from each sensor was acquired and evaluated using Hinkley and Akaike criteria. Figure 2 depicts the experimental procedure.
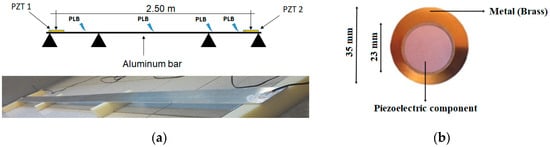
Figure 2.
(a) Experimental setup and (b) piezoelectric diaphragm.
Considering the acoustic wave propagation velocity in aluminum, VAl = 2896 m/s [14], and Equations (3) and (4), the mathematical model which describes the location of the damage, in the x direction, is given:
 where t1 and t2 are TOAs calculated via either Hinkley or Akaike criteria, and Δt2,1 is the difference between t1 and t2.
where t1 and t2 are TOAs calculated via either Hinkley or Akaike criteria, and Δt2,1 is the difference between t1 and t2.

5. Results and Discussion
Figure 3 illustrates the raw signal arisen from the sensors for x = 0.5 m. In order to summarize the results, the data shown here will be related to x = 0.5 m only.
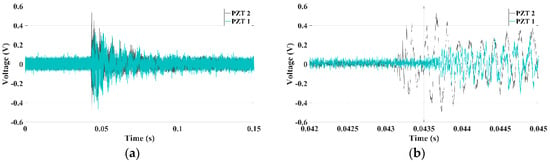
Figure 3.
Signals to disturbance at 0.5 m: (a) total duration; (b) zoom.
The low-cost transductors were sensitive to the acoustic waves generated by PLB as impulsive signals were acquired, as shown in Figure 3. However, there were uncertainties regarding the determination of arrival time of the signal in each sensor, according to Figure 3b, which indicate the necessity to apply either Hinkley or Akaike to correctly locate the damage.
According to Figure 4, signal for x = 0.5, the excitation time using Hinkley and Akaike criteria were based on the minimum from each curve, 325 and 305 µs, respectively. The difference between these two criteria is due to the uncertainty in the beginning of the signal acquisition, which is calculated using autoregressive algorithms. Based on such excitation times, the location of the damage was calculated using Equations (7)–(9), and the data are presented in Table 1.
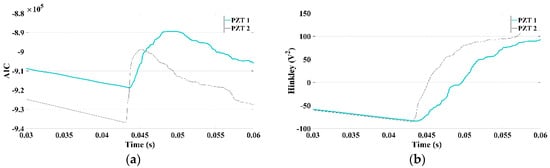
Figure 4.
Signal analyzed for damage at x = 0.5 m: (a) via Hinkley; (b) via Akaike.

Table 1.
Damage location using Hinkley and Akaike criteria.
The error using the Akaike criterion was lower than the Hinkley criterion in all cases, as shown in Table 1. For Akaike, the error was between 0 and 6% and for Hinkley between 0.8 and 16%. The averaged error was 1.98% for Akaike and 5.5% for Hinkley. Although the error using Hinkley criterion was greater than that of the Akaike criterion, the precision of the former is still considered good. Considering the beam length, the maximum error using the Hinkley criterion would be 0.08 m, which does not compromise the damage location precision.
6. Conclusions
This study aimed to compare two different damage location criteria, Akaike and Hinkley. They were used to locate damage using acoustic waves and signal triangulation in metallic structures. The differences in the excitation times caused by acoustic waves propagating in an aluminum beam instrumented with low-cost piezoelectric diaphragms were analyzed to compare both methods. The results have shown that the piezoelectric diaphragms are reliable, and the Akaike criterion was more precise than the Hinkley criterion in locating damage. In future studies, it is necessary to evaluate the efficiency of such criteria for determining damage location in two or three dimensions under temperature variation.
Author Contributions
All authors contributed in writing, proofreading, and providing suggestions for the improvement of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, H.; Ren, L.; Jia, Z.; Yi, T.; Li, D. State-of-the-art in structural health monitoring of large and complex civil infrastructures. J. Civ. Struct. Health Monit. 2016, 6, 3–16. [Google Scholar] [CrossRef]
- Farrar, C.R.; Worden, K. Structural Health Monitoring: A Machine Learning Perspective; Wiley: Chichester, UK, 2013; p. 654. [Google Scholar]
- Salmanpour, M.S.; Khodaei, Z.S.; Aliabadi, M.H.F. Impact Damage Localisation with Piezoelectric Sensors under Operational and Environmental Conditions. Sensors 2017, 17, 1178. [Google Scholar] [CrossRef] [PubMed]
- Koabaz, M.; Hajzargarbashi, T.; Kundu, T.; Deschamps, M. Locating the acoustic source in an anisotropic plate. Struct. Health Monit. 2011, 11, 315–323. [Google Scholar] [CrossRef]
- Ciampa, F.; Meo, M.; Barberi, E. Impact localization in composite structures of arbitrary cross section. Struct. Health Monit. 2012, 11, 643–655. [Google Scholar] [CrossRef]
- Robles, G.; Fresno, J.M.; Tarifa, J.M.M. Separation of radio sources and localization of partial discharges in noise environments. Sensors 2015, 15, 9882–9898. [Google Scholar] [CrossRef] [PubMed]
- Markalous, S.; Tenbohlen, S.; Feser, K. Detection and Location of Partial Discharges in Power Transformers using Acoustic and Electromagnetic Signals. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 1576–1583. [Google Scholar] [CrossRef]
- De Castro, B.A.; de Melo Brunini, D.; Baptista, F.G.; Andreoli, A.L.; Ulson, J.A. Assessment of macro fiber composite sensors for measurement of acoustic partial discharge signals in power transformers. IEEE Sens. J. 2017, 17, 6090–6099. [Google Scholar] [CrossRef]
- Castro, B.A.; Clerice, G.A.; Andreoli, A.L.; de Souza Campos, F.; Ulson, J.A. A low cost system for acoustic monitoring of partial discharge in power transformer by Piezoelectric Sensor. IEEE Lat. Am. Trans. 2016, 7, 3225–3231. [Google Scholar] [CrossRef]
- Meitzler, A.H. IEEE Standard on Piezoelectricity: An American National Standard; IEEE-ANSI: New York, NY, USA, 1988; 66p. [Google Scholar]
- Budoya, D.; Castro, B.D.; Campeiro, L.; Silveira, R.D.; Freitas, E.D.; Baptista, F. Analysis of Piezoelectric Diaphragms in Impedance-Based Damage Detection in Large Structures. Proceedings 2018, 2, 131. [Google Scholar]
- De Freitas, E.S.; Baptista, F.G.; Budoya, D.E.; de Castro, B.A. Equivalent circuit of piezoelectric diaphragms for impedance-based structural health monitoring applications. IEEE Sens. J. 2017, 17, 5537–5546. [Google Scholar] [CrossRef]
- Sause, M.G.R. Investigation of pencil lead breaks as acoustic emission sources. J. Acoust. Emiss. 2011, 29, 184–196. [Google Scholar]
- Grünwald, E.; Hammer, R.; Nuster, R.; Wieser, P.A.; Hinderer, M.; Wiesler, I.; Zelsacher, R.; Ehmann, M.; Brunner, R. Simulation of Acoustic Wave Propagation in Aluminium Coatings for Material Characterization. Coat. J. 2017, 7, 2–11. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).