Numerical Simulation of Volatile Organic Compounds during Condensation in a Vertical Tube ^†

Abstract

The purpose of this study is to analyze the combined heat and mass transfer through condensation of volatile organic compounds (VOCs), particularly alcohol (n-butanol-propanol) in the presence of non-condensable gas inside a vertical tube. An implicit finite difference method is employed to solve the coupled governing equations for liquid film and gas flow together with the interfacial matching conditions. The numerical results indicate that the Transfers are more intense at the entrance of the tube for the ternary mixture and promote heat and mass exchanges.

1. Introduction

The Condensation of mixture is one technology used to reduce volatile organic compounds (VOCs) emission rates. Its use has been driven in part by the Clean Air Act Amendments of 1990, which state acceptable rates for VOCs emissions. Condensation technology allows reclamation of VOCs, providing an economic incentive when costly product is reclaimed as a condensate and can be used to protect the ozone layer in the stratosphere. One of the most harmful air pollutants are VOCs, which can be evaporated and transport to atmosphere at ambient conditions. Such materials have been making many pollution risks such as: their ability to forming undesired photochemical ozone smog, and the potential to cause carcinogenic and mutagenic [1]. Also VOCs react with stratospheric ozone causing destroying in this sphere and increasing the hole in ozone layer which protects us from ultraviolet rays [2].

Indeed, various studies have focused on the improvement of film condensation with different numerical or experimental methods using pure vapors or mixtures of vapor and non-condensable gas by studying the effect of parameters affecting this phenomenon.

The authors [3] developed a numerical study of heat and mass transfer during the condensation of water vapor and ethanol (and methanol) mixture in the presence of air. They showed that the transfers during the condensation of the ethanol vapor and methanol mixture are more influenced by the non-condensable gas compared to the water vapor.

2. Physical Model

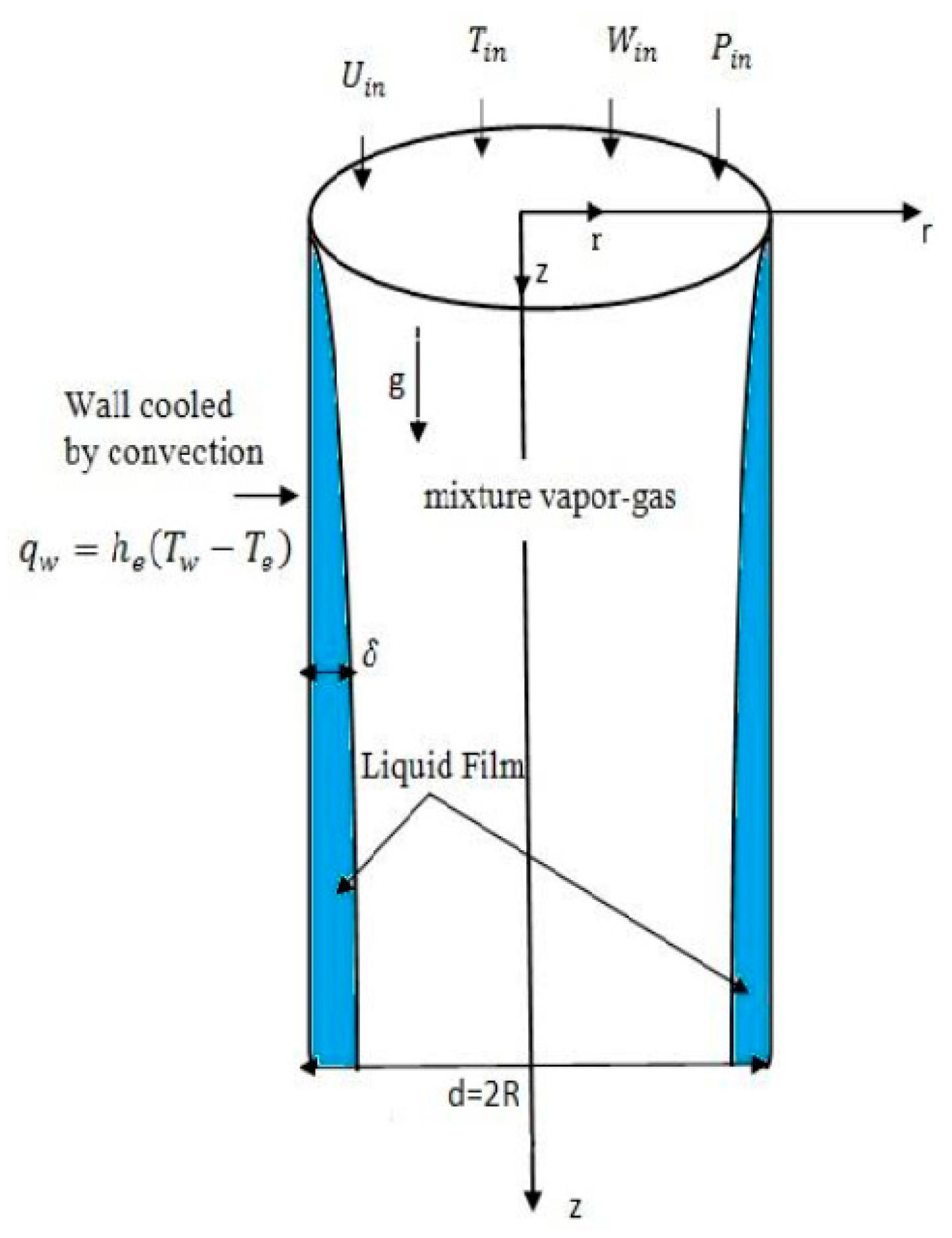
Consider a vertical tube of radius R and thickness δ_z is very small relative to R (Figure 1). At the entrance of the tube, comes a flow of vapor-air mixture with a uniform temperature T_in, uniform pressure P_in and vapor mass fraction W_in. The wall of the tube is cooled by convective in contact with an external fluid (air) at temperature T_e.

The simplifying assumptions considered are the following:

• The flow of the gas mixture is laminar and stationary.
• The flows are two-dimensional and ax symmetric.
• The radiation and effects of Duffour and Soret are negligible.
• The boundary layer approximations are valid for both phases.
• The gas mixture is considered perfect gas.
• The liquid-vapor interface is mobile, without wave, in local thermodynamic equilibrium and impermeable to dry air.
• The effect of the liquid superficial tension is negligible.

3. Equations

The equations characterizing the heat and mass transfers in the two liquid and gaseous phases are as follows:

3.1. Liquid Phae

The equations of continuity, the momentum, and energy are given as follows:

$$\frac{\partial }{\partial z}\left({\rho }_l{u}_l\right)+\frac{1}{r}\frac{\partial }{\partial r}\left(r{\rho }_l{v}_l\right)=0$$

(1)

$$\frac{\partial }{\partial z}\left({\rho }_l{u}_l^2\right)+\frac{1}{r}\left(\frac{\partial }{\partial r}\left({\rho }_{l}r{v}_l{u}_l\right)\right)=-\frac{dp}{dz}+\frac{1}{r}\frac{\partial }{\partial r}\left(r{u}_l\frac{\partial u_l}{\partial r}\right)+{\rho }_{l}g$$

(2)

$$\frac{\partial }{\partial z}\left({\rho }_l{C}_p^l{u}_l{T}_l\right)+\frac{1}{r}\frac{\partial }{\partial r}\left({\rho }_l{C}_p^{l}r{v}_l{T}_l\right)=\frac{1}{r}\frac{\partial }{\partial r}\left(r{\lambda }_l\frac{\partial T_l}{\partial r}\right)$$

(3)

3.2. Gas Phase

The equations of continuity, the momentum, energy and diffusion are given as follows:

$$\frac{\partial }{\partial z}\left({\rho }_m{u}_m\right)+\frac{1}{r}\frac{\partial }{\partial r}\left(r{\rho }_m{v}_m\right)=0$$

(4)

$$\frac{\partial }{\partial z}\left({\rho }_m{u}_m^2\right)+\frac{1}{r}\left(\frac{\partial }{\partial r}\left({\rho }_{m}r{v}_m{u}_m\right)\right)=-\frac{dp}{dz}+\frac{1}{r}\frac{\partial }{\partial r}\left(r{u}_m\frac{\partial u_m}{\partial r}\right)+{\rho }_{m}g$$

(5)

$$\begin{array}{l}\frac{\partial }{\partial z}\left({\rho }_m{C}_p^m{u}_m{T}_m\right)+\frac{1}{r}\frac{\partial }{\partial r}\left({\rho }_m{C}_p^{m}r{v}_m{T}_m\right)=\frac{1}{r}\frac{\partial }{\partial r}\left(r{\lambda }_m\frac{\partial T_m}{\partial r}\right)+\\ \frac{1}{r}\frac{\partial }{\partial r}\left[r{\rho }_{m}D\left(C_{pv}-C_{pg}\right)\right]\frac{\partial W^k}{\partial r}{T}_m\end{array}$$

(6)

$$\frac{\partial }{\partial z}\left({\rho }_m{u}_m{W}^k\right)+\frac{1}{r}\frac{\partial }{\partial r}\left({\rho }_{m}r{v}_m{W}^k\right)=\frac{1}{r}\frac{\partial }{\partial r}\left(r{\rho }_{m}D\frac{\partial W^k}{\partial r}\right) \mathrm{with} k=1, 2$$

(7)

3.3. Boundary Conditions and Interface

Associate with Equations (1)–(7), the following boundary conditions and interface:

• Condition at the tube inlet (z = 0)

$$u_m=u_{in}\hspace{1em}{T}_m=T_{in}\hspace{1em}W=W_{in}\hspace{1em}{p}_m=p_{in}$$

(8)

• Condition at the wall of the tube (r = R):

$$q_m=-{\lambda }_l{\frac{\partial T_l}{\partial r}|}_w=h_e\left(T_w-T_e\right){ \mathrm{u}}_{\mathrm{l}}=v_l=0$$

(9)

• Condition at the central axis of the tube (r = 0):

$$\frac{\partial u_m}{\partial r}=\frac{\partial T_m}{\partial r}=\frac{\partial W}{\partial r}=0{ \mathrm{v}}_{\mathrm{m}}=0$$

(10)

• Condition at the liquid-vapor interface ($r=R-{\delta }_z$)

Continuities of velocity and temperature:

$$u_I(z)=u_{m,I}=u_{l,I}{ \mathrm{T}}_{\mathrm{I}}(z)=T_{m,I}=T_{l,I}$$

(11)

Continuities of the shear stress and heat flux:

$${\tau }_I={\left[\mu \frac{\partial u}{\partial r}\right]}_{l,I}={\left[\mu \frac{\partial u}{\partial r}\right]}_{m,I}$$

(12)

The thermophysical properties of the liquid film and gas are considered variables depending on the temperature and mass fraction, are described in [4].

3.4. Numerical Resolution

The governing Equations (1)–(7) form a partial differential system that does not admit an analytical solution. They are solved numerically using a finite difference method implicit [5,6]. The method used is to approach the first derivatives in the axial direction by a difference in towards and centered by a difference in the transverse direction. At the liquid gas interface, the boundary conditions related to the continuity of shear stress and heat flow are approximated by a difference forward second-order partial derivatives for the velocity and temperature and by a difference backwards second order in the mixture. The systems of equations obtained after discretization can be written in the form of tri diagonal matrices. The resolution is then ensured by the algorithm of Thomas for the inversion of the matrices tri diagonal. The condensate film thickness is determined by the secant method according to an iterative procedure based on the conservation equation of the total condensate mass flow rate. The method of Raithby and Schneider [7] suitable for incompressible flows for pressure correction is used.

4. Presentation of Results

In order to study the effects of input parameters on ternary condensation (VOC), we dedicate this part to the analysis of the condensation of ternary n-butanol-propanol-air mixture as an example.

4.1. Effect of Temperature Difference ΔT

In this section we present the results of influence of the temperature difference ΔT = Tin − Te during the condensation of ternary mixture n-butanol-propanol-air. The operating conditions are maintained: P_in = 1 atm, Re_in = 2000, $W_{in}^{n-bu\tan ol}=0.05,{ \mathrm{W}}_{\mathrm{in}}^{\mathrm{propanol}}=0.25$ and ΔT is varied in the range [25 °C–35 °C].

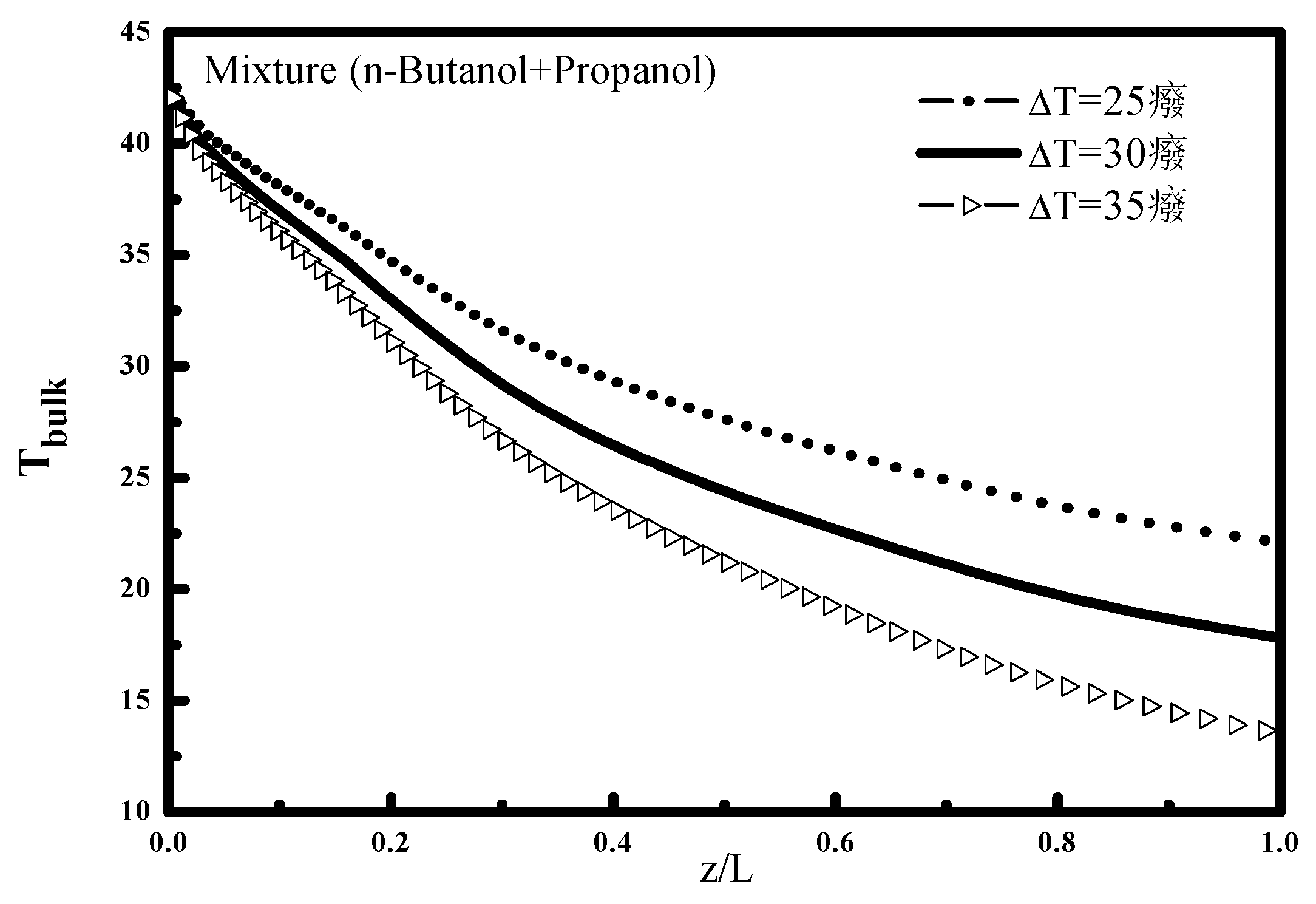
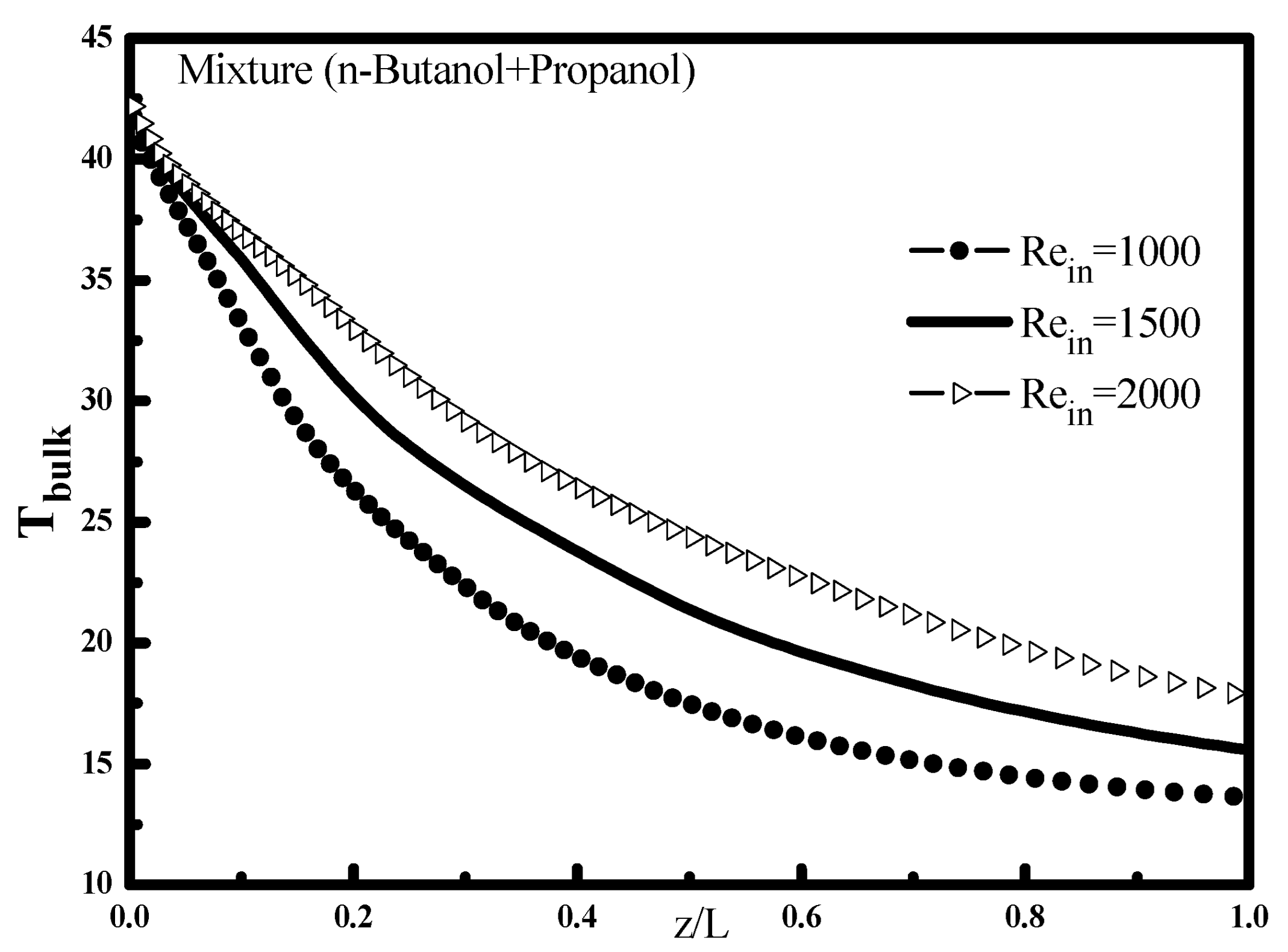
Figure 2 shows the variation of the bulk temperature T_bulk for different deviations ΔT, the increase of this temperature difference decreases the cooling external temperature, and consequently a decrease of mixture temperature along the tube. This finding is well indicated in Figure 3 which shows the variation of the Nusselt number along the tube. At the tube inlet, it is noted that the heat transfer is higher when the temperature difference is large, then it decreases and becomes independent of the ΔT at the end of condensation

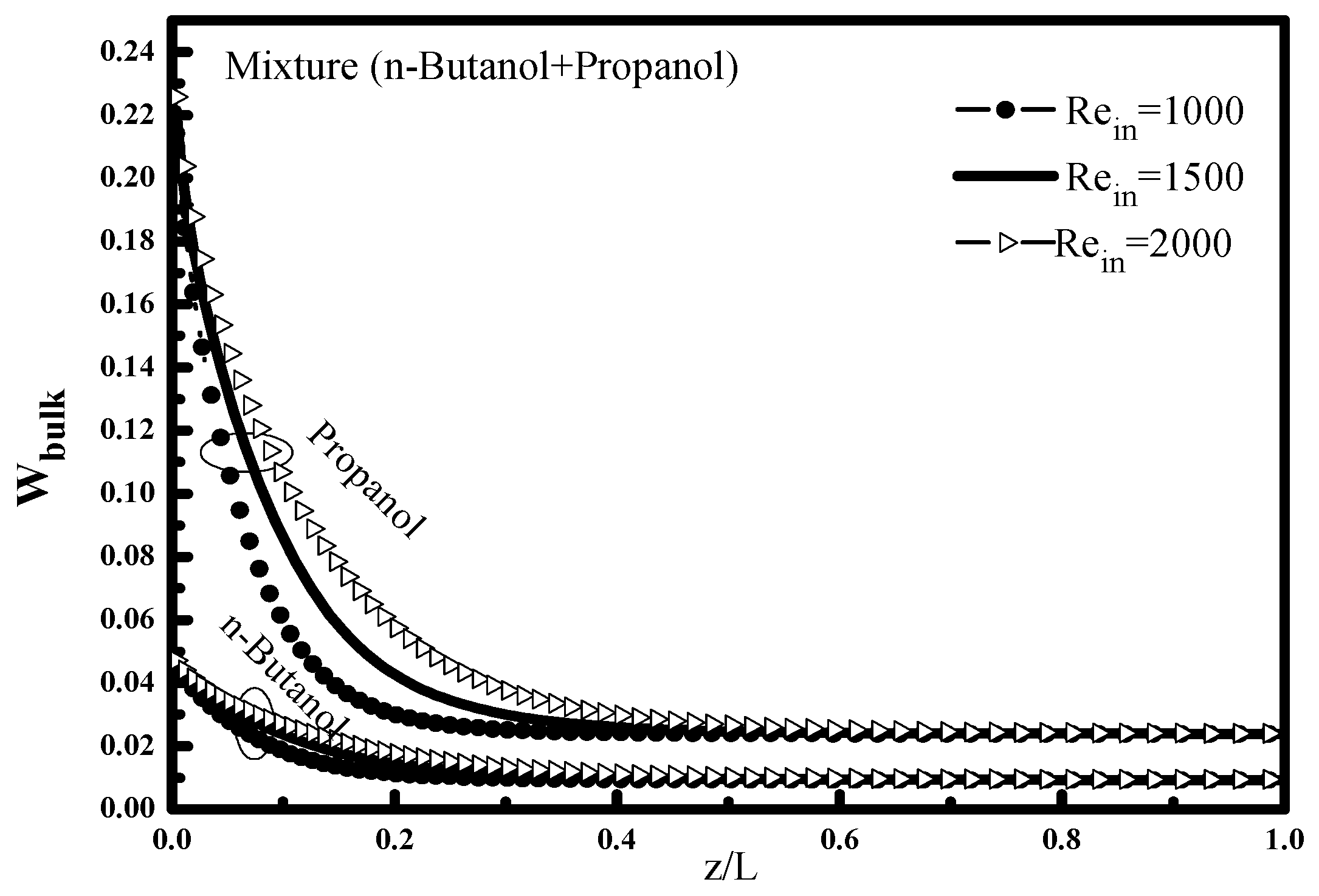
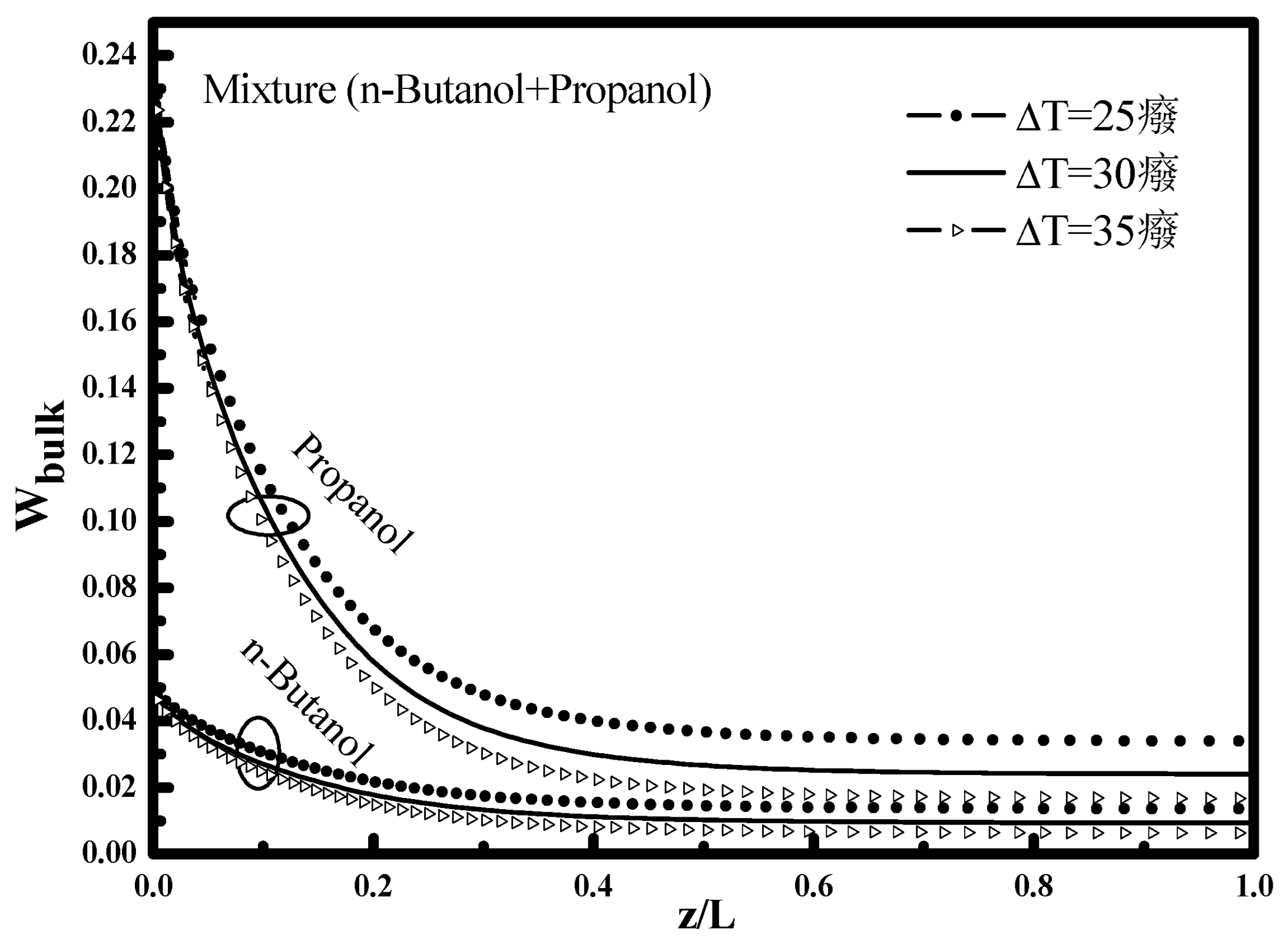
The effect of the temperature difference ΔT = T_in − T_e on the bulk mass fraction W_bulk is shown in Figure 4. At the tube inlet, it is noted that the bulk mass fraction for each compound retains its input value, and then decreases with the increasing of this temperature difference along the tube because of the vapor condensation.

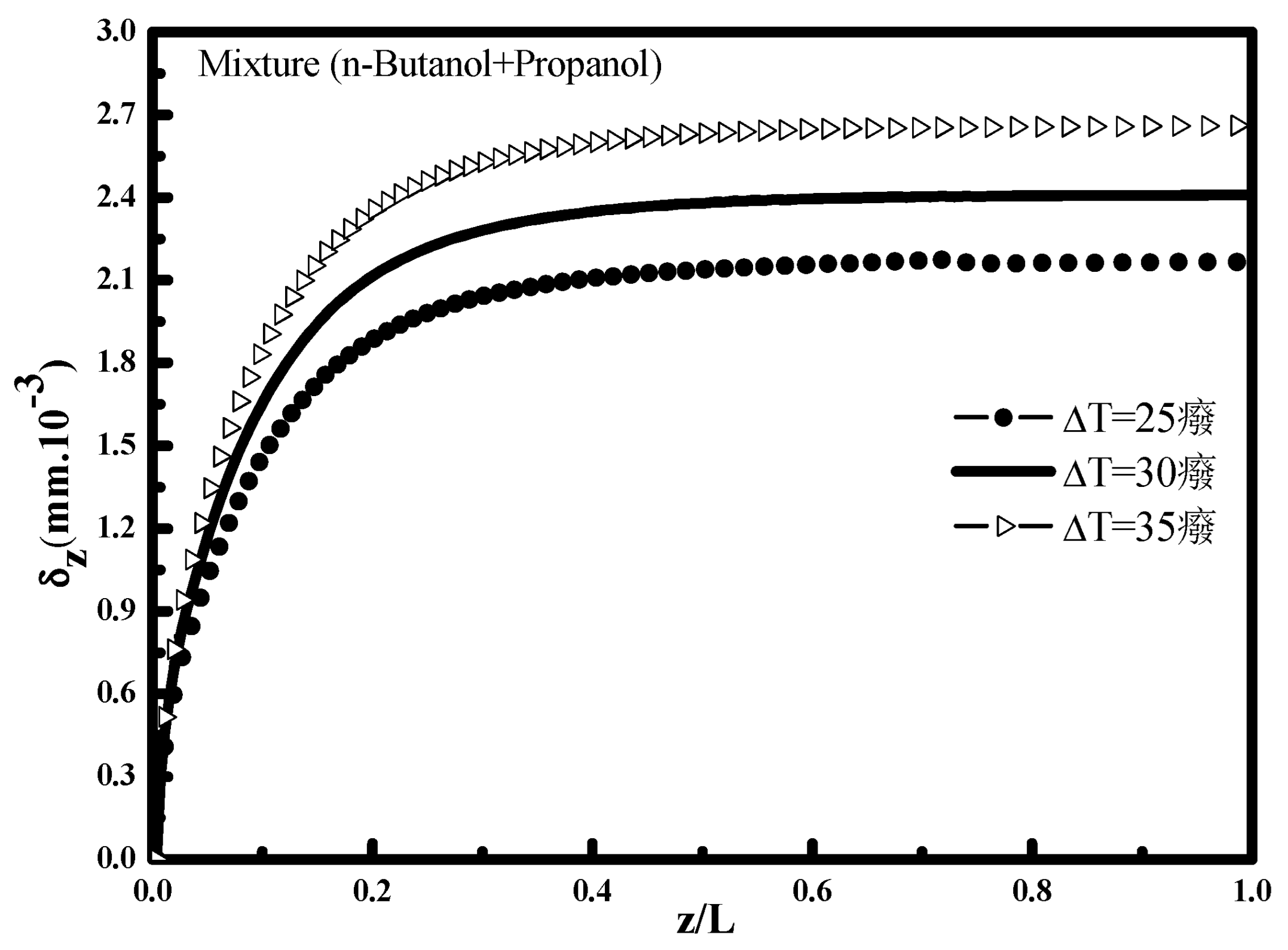
The comparison between the two mixture mass fractions n-butanol and propanol shows that the mixture mass fraction of propanol is higher at the mixture fraction of the n-butanol, which is explained by the amount of propanol vapor introduced (0.25) relative to (0.05) n-butanol in addition to saturation pressure of propanol which higher than of n-butanol. This finding is well indicated in Figure 5 which illustrates the evolution of liquid film thickness along the tube for different ΔT, an increase in the temperature difference T_in − T_e signifies a decrease in external fluid cooling temperature T_e which causes an increase in the amount of condensed vapor away from the entrance, and consequently a greater thickness.

Figure 4. Variation of the mixture mass fraction along the tube for different ΔT.

Figure 4. Variation of the mixture mass fraction along the tube for different ΔT.

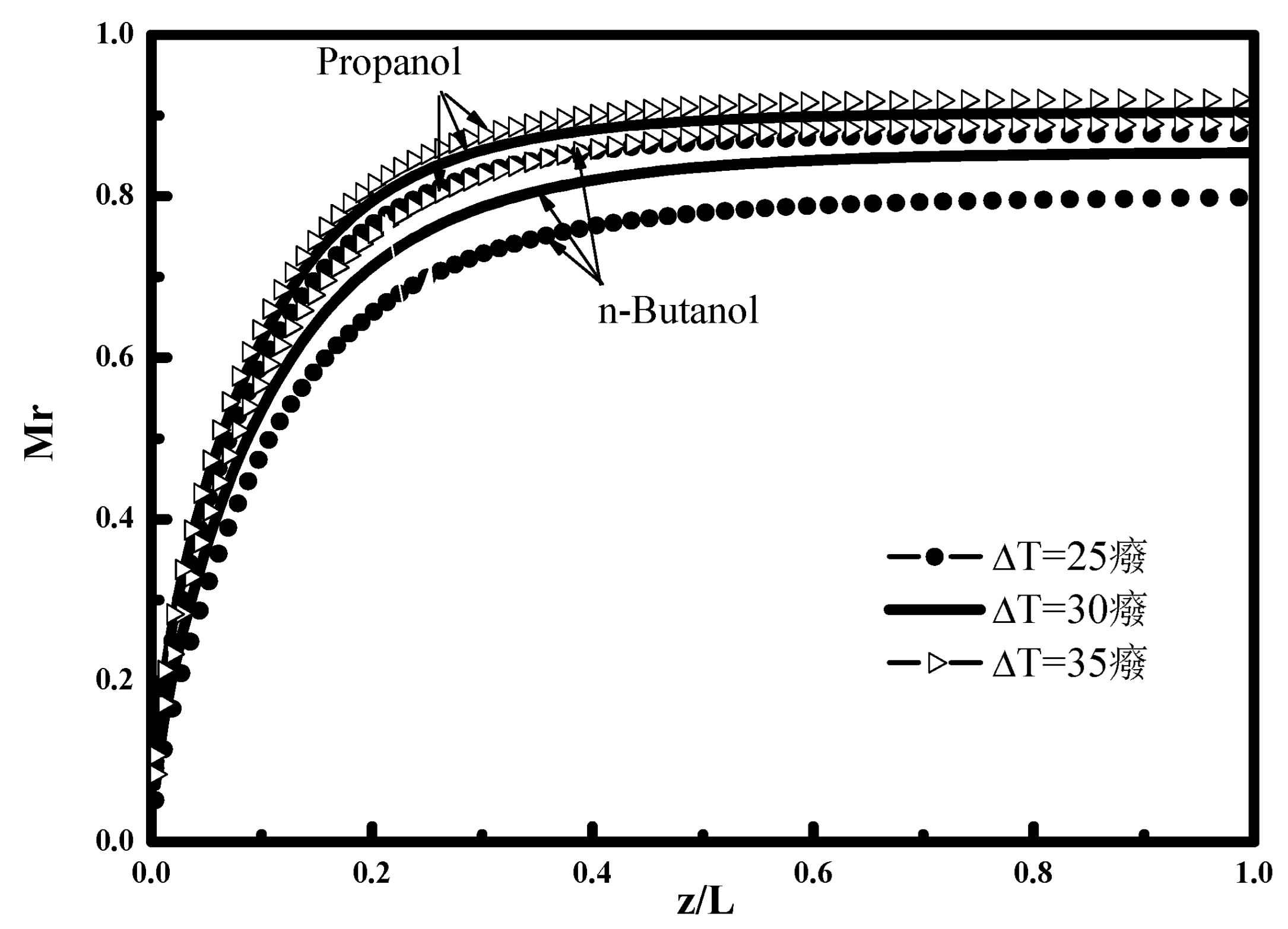
The influence of the temperature difference ΔT on the condensation rate of n-butanol and propanol vapor during the ternary mixture condensation (n-butanol-propanol-air) is illustrated in Figure 6. It can be seen that the condensation rate increases with the increase of ΔT. The increase of this difference makes it possible to favor the quantity transferred and condensed towards the condensate interface. This observation is very marked on the evolution of the condensate thickness Figure 5. The condensed vapor portion in the case of propanol vapor is more intense than in the case of n-butanol vapor. This observation is confirmed by Figure 4 which shows the bulk mass fraction. For the propanol vapor the concentration declines from W_bulk = 0.25 to 0.024 i.e., a decrease in mass fraction of 91% against 0.05 to 0.0093 i.e., with a decrease in mass fraction of 85% for the n-butanol vapor.

4.2. Effect of Reynolds Number Re_in

In this section we study the influence of the Reynolds number at the tube inlet on heat and mass transfer during the ternary mixture condensation (n-butanol propanol-air). The mass fraction of vapor of each compound $W_{in}^{n-bu\tan ol}=0.05,{ \mathrm{W}}_{\mathrm{in}}^{\mathrm{propanol}}=0.25$ the temperature difference ΔT = 30 °C and the inlet pressure P_in = 1 atm.

Figure 7 and Figure 8 illustrate the effect of Reynolds number on the bulk temperature T_bulk and the local Nusselt number N_uz for the ternary mixture (n-butanol propanol-air). It is noted that the temperature and the local Nusselt number of the mixture increase with the Reynolds number because the transfers between the vapor-air mixture and the liquid-vapor interface increase with the convection.

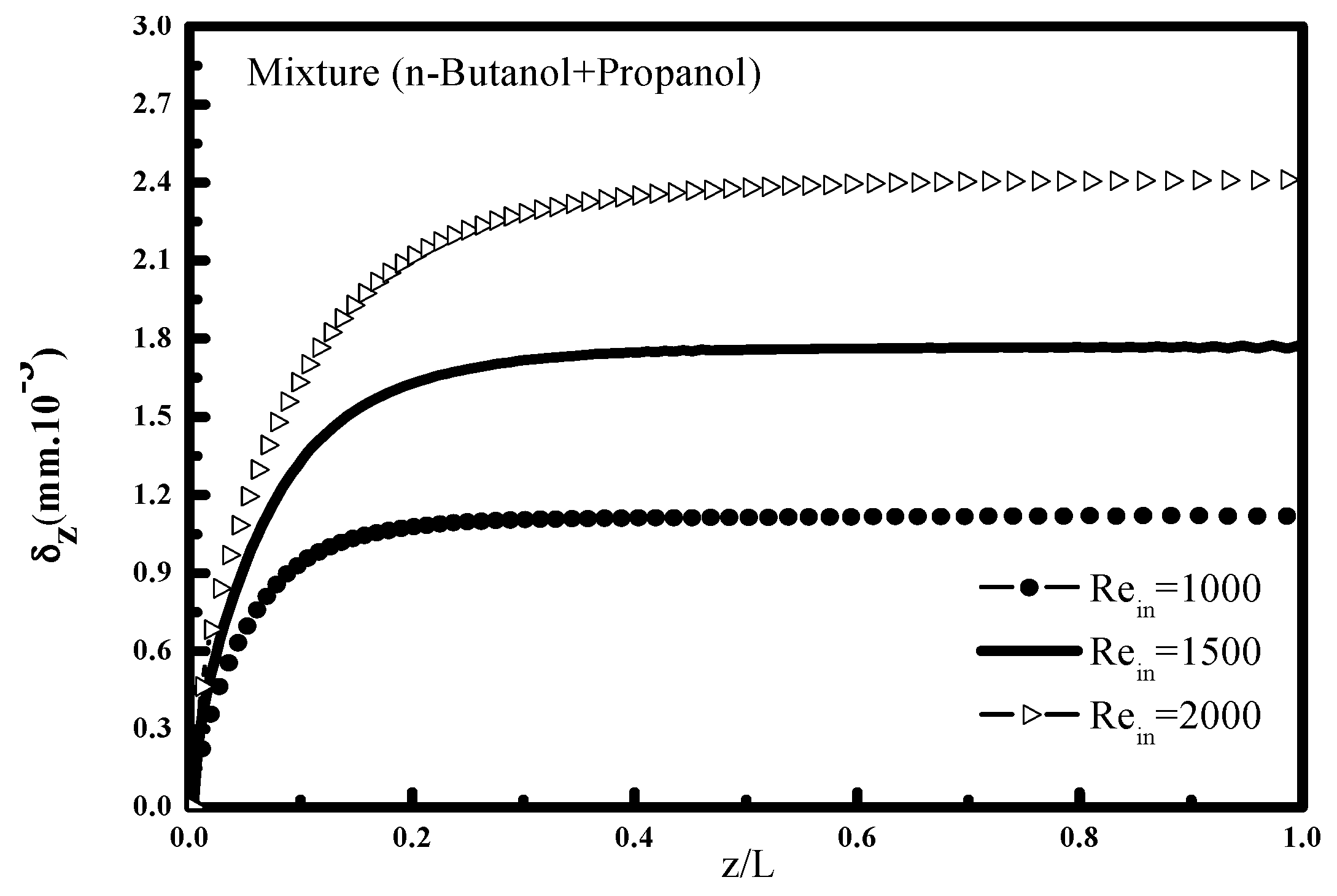
Figure 9 and Figure 10 show the effect of the input Reynolds number along the tube on the variation of the bulk mass fraction W_bulk and the liquid film thickness δ_z. It is found that the increase in the Reynolds number increases the mixture fraction of the two vapors, this is explained by the fact that the convective transfers in the vapor phase increase with the speed at which the steam mixture flows towards the vapor interface (Figure 9) which favors the increase of the condensed mass and consequently a thicker liquid film (Figure 10).

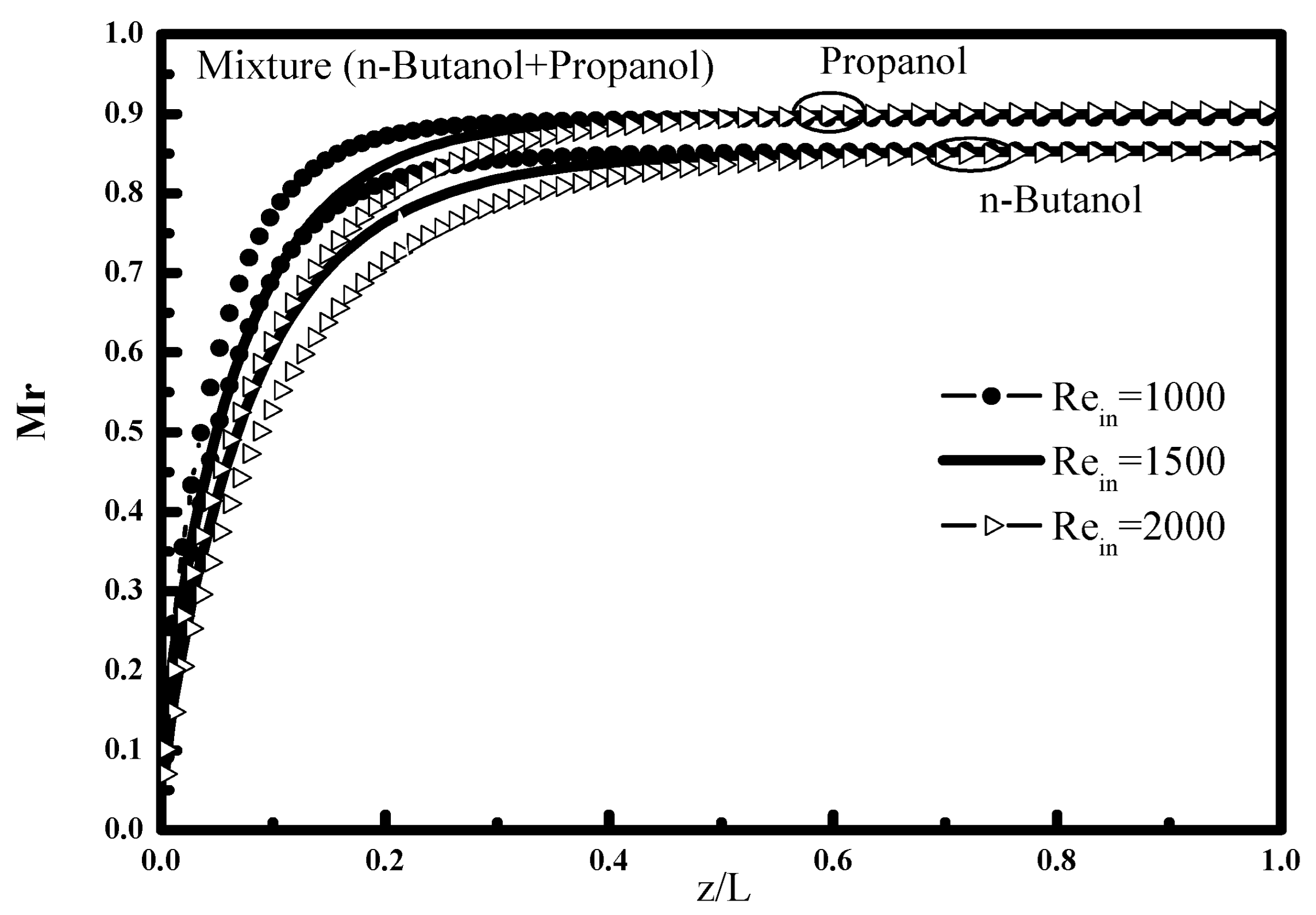
The influence of the input Reynolds number on the condensation rate along the tube is illustrated in Figure 11. It is noted that the increase in Reynolds number is accompanied by an increase in the flow of vapors at the inlet and consequently a reduced condensation rate. The comparison of condensed content of the two n-butanol and propanol vapors is due to the difference of the densities and the saturation pressures of the two vapors.

5. Conclusions

In this work, we presented the results concerning the ternary mixture condensation (n-butanol-propanol-air). Calculations made it possible to determine the mixture temperature, the mixture mass fraction, the liquid film thickness, the Nusselt number and the condensation rate. The main findings regarding efficiency of the system show that:

• Transfers are more intense at the entrance of the tube for the ternary mixture and promote heat and mass exchanges resulting in a large number of Nusselt which will gradually decrease to the exit where the curve meets at the end of condensation.
• The Nusselt number, the condensation rate and the film thickness increase with the temperature difference ΔT = T_in − T_e
• The increase in the Reynolds number at the inlet leads to an increase in the liquid film thickness, the Nusselt number and a decrease in the condensation rate.