Abstract
The spin echo experiment is an important tool in magnetic resonance for exploring the coupling of spin systems to their local environment. The strong couplings in a typical Electron Spin Resonance (ESR) experiment lead to rapid relaxation effects that puts significant technical constraints on the kinds of time domain experiments that one can perform in ESR. Recent developments in high frequency ESR hardware have opened up new possibilities for utilizing phase-modulated or composite phase slice (CPS) pulses at 95 GHz and higher. In particular, we report preliminary results at 95 GHz on experiments performed with CPS pulses in studies of rapidly relaxing fluid state systems. In contemporary ESR, this has important consequences for the design of pulse sequences where, due to finite excitation bandwidths, contributions from the Hamiltonian dynamics and relaxation processes must be considered together in order to achieve a quantitative treatment of the effects of selective, finite bandwidth pulses on the spin system under study. The approach reported on here is generic and may be expected to be of use for solid state and fluid systems. In particular we indicate how our approach may be extended to higher frequencies, e.g., 240 GHz.
1. Introduction
ESR is a powerful analytical tool for studying structure and dynamics in a broad range of solid, and fluid systems. ESR studies are sensitive to processes on nanosecond to microsecond time scales and complement the range of time scales that are accessible to other magnetic resonance techniques, such as Nuclear Magnetic Resonance (NMR). In the hands of NMR spectroscopists, time domain, or pulse techniques, have proven to be highly useful and flexible for the study of specific interactions that are not readily resolved by frequency domain, or continuous wave, techniques. The development of CPS pulse techniques in NMR, which address the limitations of real, non-ideal pulses, benefitted from the ready availability of suitable radio frequency amplifiers, phase modulators, and receiver technology. Equivalents suitable for ESR rely on the more complex microwave or even millimeter wave technology, due to the faster time scales and excitation frequencies relevant for ESR vis-à-vis NMR. In the ESR case, the bandwidth of a typical ESR spectrum and the limited power output, relatively speaking, has limited the adoption of CPS techniques. Recent advances in millimeter wave technology have called for a reassessment of this conventional wisdom, and we report on intial successes in applying CPS pulse technology at 95 GHz. The behavior of spin systems and their response to coherent perturbations may be quantified by the von Neumann entropy. Space limitations prevent anything more than a cursory discussion of this important concept. In order to develop CPS pulse sequences, extensive computations are necessary to model CPS pulse parameters, and early work used drastic approximations in order to explore a reasonable range of CPS pulse parameter space. With the advent of cheap, fast computing, these limitations are not so stringent as before, and our initial success provides the impetus for developing more computationally intensive parameter optimization methods for higher frequency ESR pulse work, where spectral extent and relaxation effects are expected to play an even more significant role. This contribution presents theoretical and experimental results that point the way to significant future applications. In Section 2 we discuss the necessary theoretical background for understanding the spin evolution equation of motion and its solution in practical cases. We have tried to indicate where approximations are made and their expected domain of validity. Preliminary results demonstrating the utility of the theoretical formalism and its application to CPS pulse specification is given in Section 3. We put these results in broader context and indicate directions for future work in Section 4.
2. Spin Evolution
The Stochastic Liouville Equation (SLE) is an important tool for studying the response of a spin system to external magnetic perturbations. The SLE achieves this by quantifying the properties of the spin system via the density matrix formalism and modeling external perturbations by incorporating their effects in an equation of motion for the density matrix. The resulting equation of motion consists of two parts which may be interpreted in terms of classical analogues. The conservative, Hamiltonian dynamics may be understood in terms of a classical dipole model, where the response is governed by a torque equation. Couplings of the spin system to its surroundings are governed by dissipative processes that may be thought of as frictional torques. These considerations may be quantified as follows
In Equation (1), the density matrix is perturbed from its equilibrium value by a time-dependent Hamiltonian which describes the conservative dynamics. The dissipative contributions to the dynamics modeling the recovery of the spin system to equilibrium are quantified by the relaxation operator . As it stands, Equation (1) is very general. For the purposes of this contribution, we will apply it to a system of weakly interacting spin 1/2 magnetic dipoles perturbed by a time-dependent Zeeman interaction. The expectation value of the spin angular momentum is computed via the defining relation
The expectation value of the spin computed from Equation (2) may be related to the observed magnetic dipole by identifying
The constant of proportionality is the gyromagnetic ratio which is proportional to where m is the mass of the relevant spin bearing charge. In ESR this is usually an unpaired electron which may arise from a crystalline defect, or be introduced via chemical means into a molecular system of interest. From a practical perspective, electron magnetic moments are typically on the order of 1000 times larger than nuclear magnetic moments due to the factor, and this has important consequences for the technology used for perturbing the ESR spin system and monitoring its recovery to equilibrium.
The Zeeman interaction of a magnetic dipole in an applied time-dependent magnetic field is quantified by the following Hamiltonian
Equation (4) is the quantum mechanical generalization of the potential energy of a classical dipole in an applied magnetic field. Note that the density matrix for a system of spin 1/2 dipoles may be expanded in a set of spin 1/2 angular momentum operators. The commutator term in Equation (1) will then depend on commutators of the form
In Equation (5), is antisymmetric in all of its indices. Classically this corresponds to a cross-product and motivates the identification of the commutator term as a torque term in Equation (1). Note that we are using a Cartesian representation of the spin operators here.
For the purposes of this report, we will assume a very simple form for the relaxation operator and introduce two phenomenological relaxation times. The recovery of the spin system to equilibrium will be quantified by the spin-lattice relaxation time . The -dependent terms govern the dissipative response of the longitudinal component of the magnetization, or expectation value of . In general one neither expects nor observes that the transverse components of the magnetization, or expectation values of and , respond on the time scale. In fact, the transverse relaxation time generally satisfies the inequality . It is useful to note that one may construct more complicated relaxation operators in order to model dissipative processes, such as rotational diffusion, but that is beyond the scope of the work reported on here.
Upon computing the expectation value of the magnetization in a time-dependent field, and ignoring relaxation for the moment, the SLE becomes a torque equation for the magnetization of the spin system which can be written in the following form
Equation (6) describes the conservative Hamiltonian dynamics. When the dissipative terms are included, we also need to compute the expectation value of the equilibrium magnetization . When the relaxation terms are included, the equation of motion for the magnetization assumes the following matrix form
These are the Bloch equations, derived from the SLE, Equation (1). Note that Equation (7) is a special case of Equation (1). Equation (1) is more general than Equation (7), but Equation (7) has sufficient generality for the work reported on here. Note that Equation (7) is a set of coupled, linear, inhomogeneous first order differential equations. In order to cast this set of equations into a more tractable form, it is useful to specialize the form of the time-varying magnetic field and introduce some commonly applied approximations valid when the z component of the applied magnetic field is taken to be static and much larger in magnitude than any of the other components.
2.1. Rotating Wave Approximation
A common experimental situation is to suppose that a static field is applied along the laboratory z axis and a linearly polarized magnetic field is applied along the laboratory x axis. It is convenient to resolve the linearly polarized perturbing field into counter-rotating circularly polarized components. When this is done, the applied field is
When is large compared to , it is standard practice to drop the counterrotating component of the applied magnetic field and perform a coordinate transformation that renders both the circularly polarized applied field and the static applied field constant. This is the content of the rotating wave approximation (RWA) and the transformation to the rotating frame. A good discussion of these points may be found in Allen and Eberly []. When these transformations are made, Equation (7) takes the following matrix form
In Equation (9), is the detuning from resonance defined by the frequency of the perturbing field and the static field . In addition . Equation (9) may be solved for constant fields, which we have achieved by exploiting the RWA and transforming to the rotating frame, by Laplace transform techniques[]. The solution of this coupled set of equations when relaxation effects can be ignored is known as the Rabi Solution [].
2.2. Quantum Mechanics of Two Level Systems
In this work, we will exploit the close relationship between the SLE, Equation (1) and the Bloch Equations, Equation (7). For the present purpose, note that for a two-level system the quantum mechanical spin operators, as well as the density matrix may be represented as matrices. The density matrix is a Hermitian operator and satisfies the constraint that , so that not all elements of are independent. For a density matrix, there are in fact three independent parameters, which may be identified with the expectation values of the components of the magnetic dipole moments in the magnetic resonance problem. For more details on the density matrix formalism, Slichter [] is a good reference. As the components of the magnetization vector are sufficient to specify completely the density matrix for a two-level, or spin 1/2, system, one may think of the transformation that diagonalizes the density matrix as a series of rotations. A useful procedure in practice is to perform a rotation about the direction that rotates the expectation values of and into the plane, and then perform a rotation about the axis to transform the expectation value of to the axis. This diagonalization process is equivalent to finding the eigenvalues of the density matrix. Once the eigenvalues of the density matrix are known, one may compute matrix-valued functions in a straight-forward fashion, using, e.g., Sylvester’s Theorem. A good discussion of this point is given by Merzbacher []. In particular, one quantity of interest is the von Neumann entropy
Equation (10) is the extension of the Shannon entropy to a more general quantum mechanical setting. It is a useful tool for examining the response of spin systems to various manipulations by pulsed fields. For the present purpose, it is useful to note that the trace in Equation (10) is invariant under the matrix diagonalization process, and so the eigenvalues of the density matrix are particuarly useful here. For a two-level system, in fact,
Here is twice the expectation value of for a spin 1/2 system. Note that the von Neumann entropy is symmetric under the transformation . This symmetry gives rise to an apparent paradox in so-called inversion recovery experiments, but space constraints preclude further discussion.
2.3. Pulses and Magnetic Resonance
Many contemporary ESR experiments are performed using pulse techniques for which the density operator formalism developed above is highly useful. In general, one applies a strong time-varying pulse in the lab frame to perturb the magnetization from equilibrium and then monitors the subsequent time development of the magnetization to study details of structure and dynamics in the relevant spin system. Notice that the formalism that we developed above is most readily used when the applied fields are static, but recall that we have already made such a transformation by using the RWA and changing coordinate systems to the rotating frame. In addition, the foramlism developed above is also applicable to applied fields that are piece-wise continuous, that is, the fields in the rotating frame may be treated as constant including step discontinuities. This is an example of the flexibility of the formalism in practical applications. Consider a situation where there is a slight detuning from exact resonance, in Equation (9). Suppose further, that at time the magnetic dipole is aligned with the applied static field and has equilibrium magnetization . Now suppose that the co-rotating component of the perturbing field acts for a time so that . As we shall see, this corresponds to rotating the equilibrium magnetization by degrees in the plane. At time , the perturbing field is turned off, and the spins are allowed to precess freely. In order to quantify this behavior, it is useful to have an explicit expression for the Rabi solution for piecewise continuous fields.
The Rabi solution is an analytic solution that accounts for detunings from resonance and strong pulses in the rotating frame but does not account for relaxation effects during the pulse. For sufficiently strong pulses this would not be a serious limitation, but ESR applications typically require a more complete treatment. With these limitations in mind, the Rabi solution for a finite detuning and strong constant field along the rotating frame x axis may be written in the following form
In Equation (12) the following quantities are defined: , . For strong pulses and detunings that are not too large, one may make the useful approximations: , , . These approximations allow us to develop a useful approximate matrix equation valid to order . Under the condition that , Equation (12) becomes
For the case of exact resonance , it is easy to see that if then , corresponding to a rotation of the magnetization by around the axis.
In the absence of relaxation terms, or for times short enough that no significant relaxation has occured, it is also useful to develop the Rabi solution for free precession, that is, for the case . A straightforward computation shows that for the case ,
Note that in the absence of equilibrium inducing relaxation terms, is a constant of the motion under free precession. Thus, Equation (14) describes free precession in the plane transverse to . We may compute the precession of the transverse magnetization for a time after a pulse by inserting the solution vector, the left hand side of Equation (13), into the right hand side of Equation (14). A straightforward calculation yields the following result . One may also compute the effect of a subsequent pulse followed by a period of free precession of duration . The result of the calculation to order is as follows
Note that if then the transverse spin response is independent of the detuning, and we say that the magnetization has been refocused along the axis. The significance of this result for practical magnetic resonance spectroscopy is hard to overstate. In general, the detuning can arise from a homogeneous process which affects all spins equally, or an inhomogeneous process which has different effects on different spin cohorts. For many practical applications in magnetic resonance one may tune a spectrometer so that the spectral response is centered on a symmetric, inhomogeneous distribution of detunings caused by magnetic inhomogeneities. The total response of the system must be integrated over this inhomogeneous distribution which acts as a source of broadening that reduces the observable magnetization. When the detunings are all refocused in the planse as in Equation (15), however, the transverse spin response becomes independent of the detuning and one observes the total transverse magnetization of the resonance-active spins. Note further that during a period of free precession in the absence of relaxation effects the magnetization is a vector of constant magnitude and thus the eigenvalues of the density matrix are also constant. Thus during free precession in the absence of relaxation, the dynamics is conservative, and no change in entropy occurs.
2.4. Practical Considerations in ESR
In ESR, the relevant timescales for relaxation processes can be on the order of nanoseconds, and the spectral extent in frequency units can be much larger than . When this is so, numerical solution of Equation (7) or its density matrix equivalent Equation (1) are needed to make quantitative predictions of the response of the spin system. With a view towards establishing a formalism that may be extended to more complex systems, we return to the density matrix formalism and develop a formalism based on irreducible spherical tensor operators and treat the matrix elements of as elements of a column vector in the space of transitions, the so-called Liouville space. We may make the RWA as before and achieve an equivalent of the rotating coordinate frame by performing a Floquet analysis of the time-dependent matrix elements of the density matrix. In practice, it is found that the deviation of the density matrix from its equilibrium value is the relevant quantity. When these transformations are carried out, it is found that the matrix representation of Equation (1) takes the following form,
Equation (16) has been specialized to the case of an ensemble of spin 1/2 dipoles, but it is in a form that may be generalized along the lines discussed in Stillman and Schwartz []. The new notational features include the transition moment, and q the normalization of the equilibrium density matrix. In addition, the phase factors allow for more general perturbing fields corresponding to excitations along the or axes in the rotating frame. As Equation (16) incorporates detunings and relaxation times of arbitrary magnitude, it is the appropriate generalization of the approximate results discussed in Section 2.3. In order to make the connection to quantities observed in the laboratory, we note that is the expectation value of the operator . Note that if the matrix appearing in Equation (16) is complex symmetric. In practical applications, it is found that these values of are the relevant ones []. When the matrix representation of Equation (16) is complex symmetric, efficient methods of solution exist, particularly when the spin system is more complex than the simple case treated here []. For the purposes of this work, we retain the general form of Equation (16) in order to treat arbitrary pulse phases in the rotating frame. When the perturbing field characterized by d is piecewise continuous, one may solve Equation (16) in each domain where d is constant (in the rotating frame) and use continuity arguments to propagate the solution to the next region of continuous d. As noted by Stillman and Schwartz [], the matrix representation of Equation (16) takes the following form
In those regions where the spins evolve under free precession and the solution of Equation (18) reduces to the case covered in Section 2.3 if relaxation effects can be ignored. Note that the solution of Equation (18) requires a matrix inversion and the computation of a matrix exponential in general. This is typically a computational resource intensive calculation. For the simple case treated here, closed form expressions may be computed for and . An explicit form for the matrix inverse may be given as follows
Note that if then is complex symmetric, as is . The quantity . This determinant is also relevant for finding the eigenvalues of . Once the eigenvalues of are available, the methods given in Apostol [] or Merzbacher [] may be used to compute . For this simple problem, the eigenvalues of may be found using the methods of Nickalls []. Python scripts based on these considerations were developed in the Earle laboratory and are available on request.
3. Results
In order to accommodate the significant detunings that can occur for ESR experiments, it is possible to use CPS pulses first developed in NMR [] to achieve an optimum response of the spin system. The first application of CPS pulses to ESR was reported by Crepeau, et al. []. They developed a multiparameter search algorithm over the microwave phase and pulse slice duration to determine the optimum pulse parameters with desired spin system response. Their numerical simulations accounted for the distorting effects of detuning and a resonant structure with a finite excitation bandwidth but did not account for relaxation effects. Under these conditions, they were able to determine CPS pulse parameters that: minimized the amount of z magnetization following a pulse; optimized the amount of y magnetization after a pulse; and optimized the amount of z magnetization after a pulse. This work was carried out at X-band, corresponding to a microwave frequency of GHz.
Advances in millimeter wave technology have allowed these experiments to be revisited at higher frequencies. An ESR pulse spectrometer at 95 GHz [] was recently retrofitted with a phase-agile front end and improved sensitivity. These upgrades motivated a reexamination of CPS pulses for high field work. As a starting point, the parameters determined empirically by Crepeau, et al. [] were scaled to the larger available at 95 GHz.
Initial studies of CPS pulses following hardware and software upgrades to the ACERT 95 GHz high-power/cw spectrometer Figure 1 (right panel) were conducted culminating in the succesful demonstration of a CPS pulse at 95 GHz as shown in Figure 1 (left panel). Additional studies were performed to evaluate the performance of an arbitrary waveform generator (AWG) (WavePond DAx22000), in conjunction with the rebuilt transceiver (ELVA-1 MKII) analog/vector modulator and receiver sections. For these studies, a high power Extended Interaction Klystron (EIK) with a nominal output of 1 kW was deployed in the spectrometer TX arm as required for high power evaluation. In order to monitor the power returning to the receiver in the RX arm, a corner reflector was used at reference plane ’W’ as a proxy for the Fabry-P??rot resonator assembly typically used in a 95 GHz ESR experiment. The tests verify the performance of a CPS sequence of successive phases and timings from an early CPS paper [] that demonstrates the enhancement potential of the spectrometer’s AWG pulse capability.
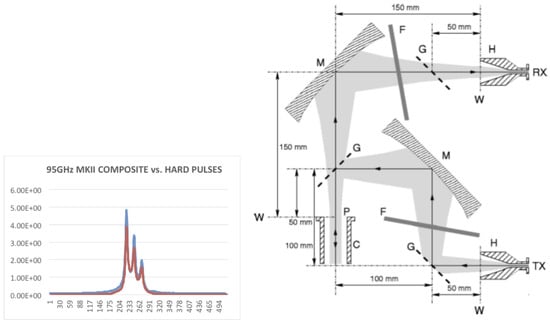
Figure 1.
Left Panel: Comparison of a CPS pulse response (red trace) to a standard full excitation hard pulse (blue trace). The three line spectrum is of a nitroxide spin label in the motional narrowing regime where the Zeeman interaction is split by a further hyperfine interaction with an Nitrogen nucleus. In this range of motion, the three hyperfine lines are only weakly coupled and evolve approximately independently. Thus their contributions to the spectrum may be simply summed. Right Panel: A schematic of the spectrometer used for these experiments. A Fabry-Pérot resonant structure (not shown) is coupled to reference plane ’W’ to perform ESR experiments.
4. Discussion
Figure 1 shows the results of a scaled emulation of an effective composite-phase sequence described by Crepeau, et al. []. The sequence reported on here consists of the sequence 9 ns/, 5 ns/, 4 ns/, 3 ns/, for a total composite pulse length of 21 ns. Reproduction of this composite pulse is of reasonably high fidelity, with the exception of some observed interference due to multiple reflections that contaminate the final (3 ns) slice. With the enhancing Fabry-Pérot resonator assembly coupled to reference plane ’W’ shown in the right panel of Figure 1, it was determined that the CPS pulse at an output power level approximately 50% of produced spectral coverage (red trace) and an effective value virtually indistinguishable from a 5 ns EIK hard pulse (blue trace). This result clearly demonstrates that a CPS pulse can successfully emulate a hard pulse of significantly shorter duration and higher peak power. Work is currently under way to extend this preliminary result to CPS pulses and thus spin echo pulse sequences. Further applications to pulse spectroscopy at higher frequencies, e.g., 240 GHz are also under way. In order to determine suitable CPS pulse characteristics at 240 GHz, we are revisiting the parameter optimization problem discussed in Section 3. This is especially timely as significant advances in computational hardware since the original studies of Crepeau, et al. [] have allowed more computationally intensive search algorithms to be usefully employed. Work is under way to extend the Laplace transform techniques reported on in this work to the CPS pulse optimization problem. For this purpose, we are developing a nested sampling approach to determine the CPS parameters that optimize the relevant cost functions for and pulses. Extensions of the methods covered here to longer pulse sequences involving three optimally phased pulses for exploring multidimensional pulse ESR spectroscopy are also under way.
Acknowledgments
The resources of the ACERT facility at Cornell University were used during the course of preparation of this manuscript.
Author Contributions
K.E. performed the theoretical analysis and O.K. developed the analysis software. K.E. wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Allen, L.; Eberly, J.H. Optical Resonance and Two-Level Atoms; Dover: New York, NY, USA, 1987; pp. 41–51. [Google Scholar]
- Stillman, A.E.; Schwartz, R.N. Theory of Electron Spin Echoes in Nonviscous and Viscous Liquids. In Time Domain Electron Spin Resonance; Kevan, L., Schwartz, R.N., Eds.; Wiley: New York, NY, USA, 1979; c. 5. [Google Scholar]
- Allen, L.; Eberly, J.H. Optical Resonance and Two-Level Atoms; Dover: New York, NY, USA, 1987; pp. 56–61. [Google Scholar]
- Slichter, C.P. Principles of Magnetic Resonance; Springer: New York, NY, USA, 1996; pp. 157–189. [Google Scholar]
- Merzbacher, E. Matrix Methods in Quantum Mechanics. Am. J. Phys. 1968, 36, 814–821. [Google Scholar] [CrossRef]
- Crepeau, R.H.; Dulčić, A.; Gorcester, J.; Saarinen, T.R.; Freed, J.H. Composite Pulses in Time-Domain ESR. J. Magn. Reson. 1989, 84, 184–190. [Google Scholar] [CrossRef]
- Schneider, D.J.; Freed, J.H. Spin Relaxation and Motional Dynamics. In Lasers, Molecules, and Methods; Hirschfelder, J.G., Wyatt, R.E., Coalson, R.D., Eds.; Wiley: Hoboken, NJ, USA, 1989; c. 10. [Google Scholar]
- Apostol, T.M. Some Explicit Formulas for the Exponential Matrix exp(At). Am. Math. Mon. 1969, 76, 289–292. [Google Scholar]
- Nickalls, R.W.D. A New Approach to Solving the Cubic: Cardano’s Solution Revealed. Math. Gaz. 1993, 77, 354–359. [Google Scholar] [CrossRef]
- Levitt, M.H. Compensation for Pulse Imperfections in NMR Spin Echo Experiments. J. Magn. Reson. 1982, 43, 65–80. [Google Scholar] [CrossRef]
- Hofbauer, W.K.; Earle, A.; Dunnam, C.R.; Moscicki, J.K.; Freed, J.H. High-power 95GHz Pulsed Electron Spin Resonance Spectrometer. Rev. Sci. Inst. 2004, 75, 1194–1208. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).