A Complete Classification and Clustering Model to Account for Continuous and Categorical Data in Presence of Missing Values and Outliers †
Abstract
:1. Introduction
- The location mixture model [9] that assumes that continuous variables follow a multivariate Gaussian distribution conditionally on both component and categorical variables.
- The underlying variables mixture model [10] that assumes that each discrete variable arises from a latent continuous variable and that all continuous variables follow a Gaussian mixture model.
2. Mixed-Type Data
2.1. Assumptions on Mixed-Type Data
- is a vector of d continuous variables,
- is a vector of q categorical variables where is the tensor gathering each space of events that can take .
2.2. Distribution of Mixed-Type Data
2.3. Outlier Handling
2.4. Missing Data Handling
3. Model and Inference
3.1. Model
- are the observed features,
- are the latent variables modelling the missing features,
- the independent labels for continuous and categorical observations
- the scale latent variables handling outliers for quantitative data and distributed according to a Gamma distribution with shape and rate parameters ,
- are the weights related to component distributions,
- the mean and the variance parameters of quantitative data for each cluster,
- the weights of the multivariate Categorical distribution of categorical data for each cluster.
3.2. Variational Bayesian Inference
3.3. Classification and Clustering
4. Application
4.1. Data
4.2. Classification Experiment
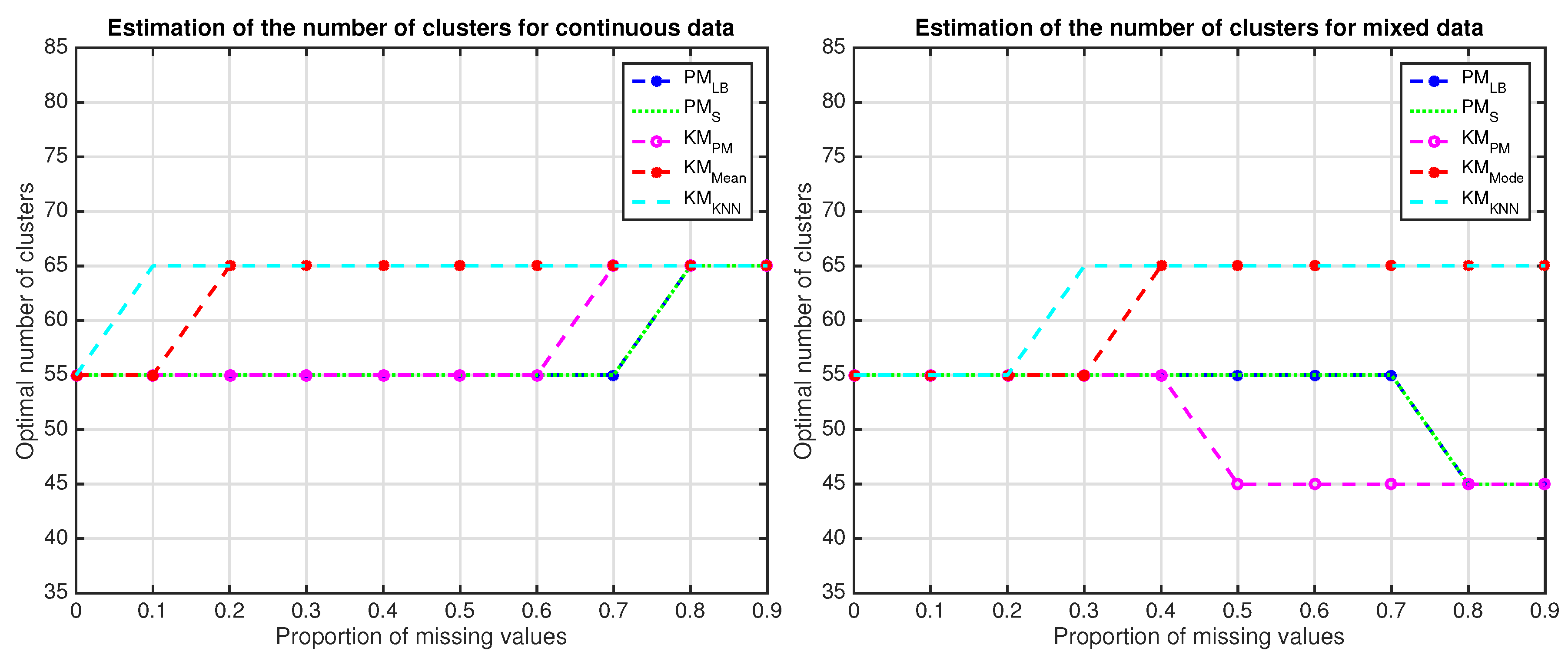
4.3. Clustering Experiment
5. Conclusions
References
- Bishop, C.M. Pattern Recognition and Machine Learning (Information Science and Statistics); Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A k-means clustering algorithm. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise; Kdd: Portland, OR, USA, 1996; Volume 96, pp. 226–231. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X. Density-Based clustering in spatial databases: The algorithm GDBSCAN and its applications. Data Min. Knowl. Discov. 1998, 2, 169–194. [Google Scholar] [CrossRef]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Troyanskaya, O.; Cantor, M.; Sherlock, G.; Brown, P.; Hastie, T.; Tibshirani, R.; Botstein, D.; Altman, R.B. Missing value estimation methods for DNA microarrays. Bioinformatics 2001, 17, 520–525. [Google Scholar] [CrossRef] [PubMed]
- Biernacki, C.; Celeux, G.; Govaert, G. Assessing a mixture model for clustering with the integrated completed likelihood. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 719–725. [Google Scholar] [CrossRef]
- Lawrence, C.J.; Krzanowski, W.J. Mixture separation for mixed-mode data. Stat. Comput. 1996, 6, 85–92. [Google Scholar] [CrossRef]
- Everitt, B. A finite mixture model for the clustering of mixed-mode data. Stat. Probab. Lett. 1988, 6, 305–309. [Google Scholar] [CrossRef]
- Andrews, D.F.; Mallows, C.L. Scale Mixtures of Normal Distributions. J. R. Stat. Soc. Ser. B (Methodol.) 1974, 36, 99–102. [Google Scholar] [CrossRef]
- Waterhouse, S.; MacKay, D.; Robinson, T. Bayesian methods for mixtures of experts. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1996; pp. 351–357. [Google Scholar]
- Schleher, D.C. Introduction to Electronic Warfare; Technical report; Eaton Corp., AIL Div.: Deer Park, NY, USA, 1986. [Google Scholar]
- Richards, M.A. Fundamentals of Radar Signal Processing; McGraw-Hill Education: New York, NY, USA, 2005. [Google Scholar]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Selected Papers of Hirotugu Akaike; Springer: New York, NY, USA, 1998; pp. 199–213. [Google Scholar]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- García-Laencina, P.J.; Sancho-Gómez, J.L.; Figueiras-Vidal, A.R. Pattern classification with missing data: A review. Neural Comput. Appl. 2010, 19, 263–282. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data: An Introduction to Cluster Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2009; Volume 344. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Revillon, G.; Mohammad-Djafari, A. A Complete Classification and Clustering Model to Account for Continuous and Categorical Data in Presence of Missing Values and Outliers †. Proceedings 2019, 33, 23. https://doi.org/10.3390/proceedings2019033023
Revillon G, Mohammad-Djafari A. A Complete Classification and Clustering Model to Account for Continuous and Categorical Data in Presence of Missing Values and Outliers †. Proceedings. 2019; 33(1):23. https://doi.org/10.3390/proceedings2019033023
Chicago/Turabian StyleRevillon, Guillaume, and Ali Mohammad-Djafari. 2019. "A Complete Classification and Clustering Model to Account for Continuous and Categorical Data in Presence of Missing Values and Outliers †" Proceedings 33, no. 1: 23. https://doi.org/10.3390/proceedings2019033023
APA StyleRevillon, G., & Mohammad-Djafari, A. (2019). A Complete Classification and Clustering Model to Account for Continuous and Categorical Data in Presence of Missing Values and Outliers †. Proceedings, 33(1), 23. https://doi.org/10.3390/proceedings2019033023





