Abstract
The weaving of flexible electronic filaments directly into the body of textiles during manufacture represents the state-of-the-art process for integrating electronic functionality into fabrics in a manner that obscures the presence of the electronics from the wearer. The reliability of emerging prototypes under typical stresses from washing and bending is primarily dependent on the durability of the electrical conductors and on their interconnections with the electronic components attached to them on polyimide filaments. To improve the durability of these filaments, this paper uses the classical beam theory to investigate the material characteristics (thickness and elastic modulus) and suitability of different encapsulations such as polyimide, polyurethane, mylar, and PEEK films for limiting the mechanical stress on the electrical conductors.
1. Introduction
Electrical conductors are necessary for transmitting information and/or energy within e-textile circuits. Research literatures are replete with examples of electrical conductors in the form of printed inks, conductive threads, thin film metals, and etched copper films that have been implemented on textiles for interconnecting surface-mount electronic components and, in some cases, for fabricating the electronics themselves on the fabric [1,2]. One of the major failure mechanisms of the resulting e-textiles is the cracking of the electrical conductors under bending and washing stresses [3,4,5].
This paper builds on [6], which reports the state-of-the-art process for integrating flexible electronic filament circuits in textiles. The circuits are fabricated on 2 mm wide polyimide filaments containing 18 µm thick copper conductors and are concealed in the textile in a weaving process. The textile houses the filaments and provides protection for the copper film, surviving up to 1500 bending cycles at a radius of 10 mm [6]. To enhance the durability of these filaments, this paper mathematically models the electronic filament as a beam, shown in Figure 1a, using the classical beam theory. The material characteristics (elastic modulus and thickness) of the encapsulation are used to tune the position the copper film about the neutral axis (NA) and control the overall stiffness of the filament. The model is also used to evaluate how the thickness of the copper layer affects the reliability of the filament.
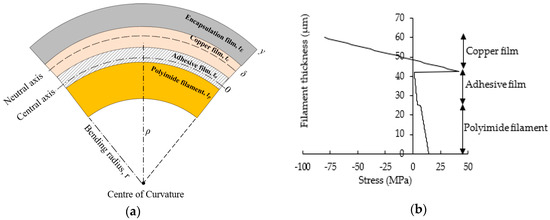
Figure 1.
(a) Bending of an encapsulated electronic filament under a bending radius of ρ, with neutral axis located at a position δ from the centre. (b) Stress distribution within an unencapsulated filament.
2. Modelling the Electronic Filament
The NA position of the electronic filament without the encapsulation film, shown in Figure 1a, is 48.5 µm, based on Equation (1) and the material properties listed Table 1. This shows that the NA position is within the copper film. The stress distribution within the filament in Figure 1b obtained from Equation (2) for a bending radius of 10 mm shows that the copper film is dominated by compressive (or negative) stress, as shown in Figure 1b. To improve the durability of the copper film, encapsulation is needed to shift the NA position to the center of the copper film to ensure the stress is symmetrically distributed.
where ‘n’, Ei, and ti are the total number of layers, elastic modulus, and thickness of the ‘ith’ layers in the filament, respectively. “y” is any arbitrary position within the filament and “x” is the layer width.

Table 1.
Material properties of electronic filament.
The relationship between the elastic modulus of the encapsulant and the thickness required to move the position of the NA within the copper film is shown in Figure 2. When elastomers (E ≤ 3 MPa) such as the VPT 9074 are used, the encapsulation thickness can be as high as 8 mm; for higher elastic modulus polymers (3 GPa ≤ E ≤ 30 GPa) such as polyimide, PEEK, and mylar, the required thickness is less than 40 µm. Figure 3 shows that polyimide encapsulation shifts the NA to the center of the copper film and evenly distributes the stress within the film. Unlike in Figure 1b, the compressive and tensile stress (i.e., 60 MPa) on the film are now equal. However, the copper film still has the highest stress during bending. To prevent this, it is necessary for the copper film thickness to reduce so that the entire copper film can be on or very close to the neutral axis where the stress amplitude is at its minimum.
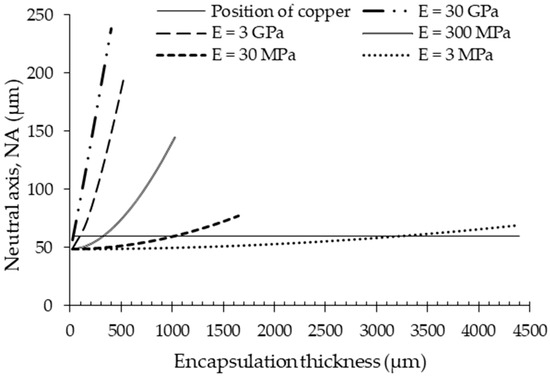
Figure 2.
Effect of the thickness and elastic modulus, E, of an encapsulation material on the position of the copper conductor relative to the neutral axis position.
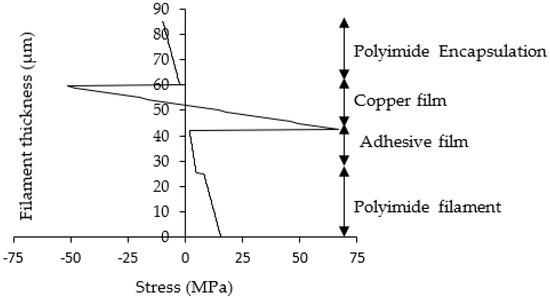
Figure 3.
Stress distribution within the electronic filament when the neutral axis (NA) is at the center of the copper film.
Figure 4 illustrates the case where the copper film thickness (1 µm) is much less than the thickness of the polyimide filament. In contrast to Figure 4, the copper film has the lowest stress amplitude of 2 MPa within the filament and does not noticeably dominate the bending characteristics of the filament. However, reducing the thickness of the conductor will reduce electrical conductivity of the filament. Therefore, depending on the e-textile application, filament design will involve a compromise between the electrical conductivity and the durability.
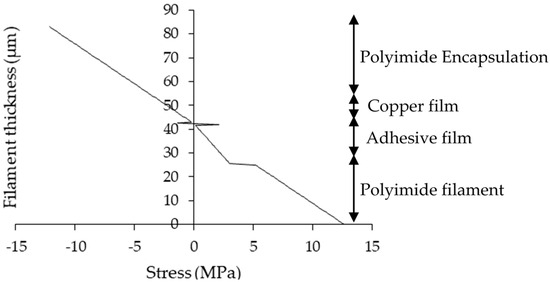
Figure 4.
Stress distribution within the electronic filament when the NA is at the center of a 1 µm thick copper film.
Finally, Table 1 shows the impact of the encapsulation thickness on the overall filament stiffness which was calculated using Equation (3). For example, with the PEEK, polyimide, and mylar encapsulants, the total filament stiffness tripled. The VPT 9074 film increases the stiffness by a factor of 8000 and is not suitable for tuning the NA position. However, at lower thicknesses (≤100 µm), it can be used to physically protect the copper film from abrasion or moisture without any change in the filament stiffness and the NA position.
3. Conclusions
This paper discussed the durability of electronic filaments where the NA position is already within the electrical conductor. For polyimide filaments containing 18 µm thick copper films, the encapsulation material improves durability by ensuring the induced stress is uniformly distributed within the copper. It does not position the entire film on the NA. By reducing the thickness of the copper film (≤1 µm), the entire film can be positioned on or close to the NA where the stress is minimum. In both cases, the same encapsulation thickness is required, and the stiffness of the encapsulated filament is up to three times the value before encapsulation. For encapsulant materials such as PEEK, polyimide, and mylar (E ≈ 3 GPa), a thickness of 40 µm is enough to place the copper film on the NA.
Funding
This work was funded by the WEARPLEX project in the Horizon 2020 EU funding—ICT-02-2018.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kim, Y.; Kim, H.; Yoo, H.J. Electrical characterization of screen-printed circuits on the fabric. IEEE Trans. Adv. Packag. 2009, 33, 196–205. [Google Scholar]
- Cherenack, K.; van Pieterson, L. Smart textiles: Challenges and opportunities. J. Appl. Phys. 2012, 112, 091301. [Google Scholar] [CrossRef]
- Li, M.; Tudor, J.; Torah, R.; Beeby, S. Stress analysis of flexible packaging for the integration of electronic components within woven textiles. In Proceedings of the 2017 IEEE 67th Electronic Components and Technology Conference (ECTC), Orlando, FL, USA, 30 May–2 June 2017; pp. 2133–2138. [Google Scholar]
- Zysset, C.; Kinkeldei, T.; Münzenrieder, N.; Petti, L.; Salvatore, G.; Tröster, G. Combining electronics on flexible plastic strips with textiles. Text. Res. J. 2013, 83, 1130–1142. [Google Scholar] [CrossRef]
- Komolafe, A. Reliability and Interconnections for Printed Circuits on Fabrics. Ph.D. Thesis, University of Southampton, Southampton, UK, 2016. [Google Scholar]
- Komolafe, A.; Torah, R.; Wei, Y.; Nunes-Matos, H.; Li, M.; Hardy, D.; Dias, T.; Tudor, M.; Beeby, S. Integrating Flexible Filament Circuits for E-Textile Applications. Adv. Mater. Technol. 2019, 1900176. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).