Information Geometry Conflicts With Independence ^†

Abstract

Information Geometry conflicts with the independence that is required for science and for rational inference generally.

1. Introduction

Information Geometry [1] assigns a geometrical relationship between probability distributions, using the local curvature (Hessian) of the Kullback-Leibler formula

$$H(\mathbf{p};\mathbf{q})=\sum _{i}p\left(i\right)log\frac{p\left(i\right)}{q\left(i\right)}$$

(1)

as the covariant geometrical metric tensor [2,3] between $\mathbf{q}$ and $\mathbf{p}$. On a n-dimensional manifold $\mathbf{p}\left(\theta \right)$ specified by parameters ${\theta }^1,\cdots ,{\theta }^n$, this $n\times n$ Riemannian metric g is

$$g_{jk}\left(\theta \right)=\sum _{i}p(i\mid \theta )\frac{\partial logp(i\mid \theta )}{\partial {\theta }^j}\frac{\partial logp(i\mid \theta )}{\partial {\theta }^k}\hspace{1em}(\mathrm{or}\int dt p(t\mid \theta )\dots \mathrm{in}\mathrm{continuum}\mathrm{form})$$

(2)

Geodesic lengths ℓ and invariant volumes V follow from ${(d\mathsf{\ell })}^2=\sum g_{jk}d{\theta }^{j}d{\theta }^k$ and $dV=\sqrt{detg}{d}^n\theta$.

Necessarily, lengths are symmetric $\mathsf{\ell }(\mathbf{p},\mathbf{q})=\mathsf{\ell }(\mathbf{q},\mathbf{p})$ between source and destination, so cannot be isomorphic to H which is from-to asymmetric. Yet (1) is the only connection which preserves independence of separate distributions, $H(\mathbf{x}\times \mathbf{p};\mathbf{y}\times \mathbf{q})=H(\mathbf{x};\mathbf{y})+H(\mathbf{p};\mathbf{q})$. Specifically, when H is used to assign an optimal $\mathbf{p}$ (meaning minimally distorted from $\mathbf{q}$) under constraints, that “maximum entropy” selection also depends on separate optimisation $\mathbf{x}$-from-$\mathbf{y}$ unless H has the form (1) [4,5].

It follows that any imposed geometrical connection must introduce interference between supposedly separate distributions. That behaviour is incompatible with the practice of scientific inference, and is confirmed by a counter-example.

2. Counter-Example

Consider the 2-parameter family of probability distributions [6]

$${\mathbf{p}}_{vw}\left(t(\mathrm{mod}1)\right)=\left\{\begin{array}{cc}{\displaystyle f\left(\frac{t-v}{w}\right)}\hfill & \mathrm{for}v<t<v+w,\hfill \\ {\displaystyle f\left(\frac{1+v-t}{1-w}\right)}\hfill & \mathrm{for}v+w<t<v+1,\hfill \end{array}\right.$$

(3)

Parameters v (location) and w (width) lie between 0 and 1. The function f (Figure 1) is monotonically increasing so that it rises from $f\left(0\right)$ at $t=v$ to $f\left(1\right)$ at $t=v+w(\mathrm{mod}1)$ before falling back to $f\left(0\right)$ at $t=v+1(\mathrm{mod}1)$. It is positive and normalised to ${\int }_0^{1}f\left(u\right)du=1$ so that the $p_{vw}(·)$’s can be probability distributions on the interval (0,1) — which could model growth and decay in a periodic system.

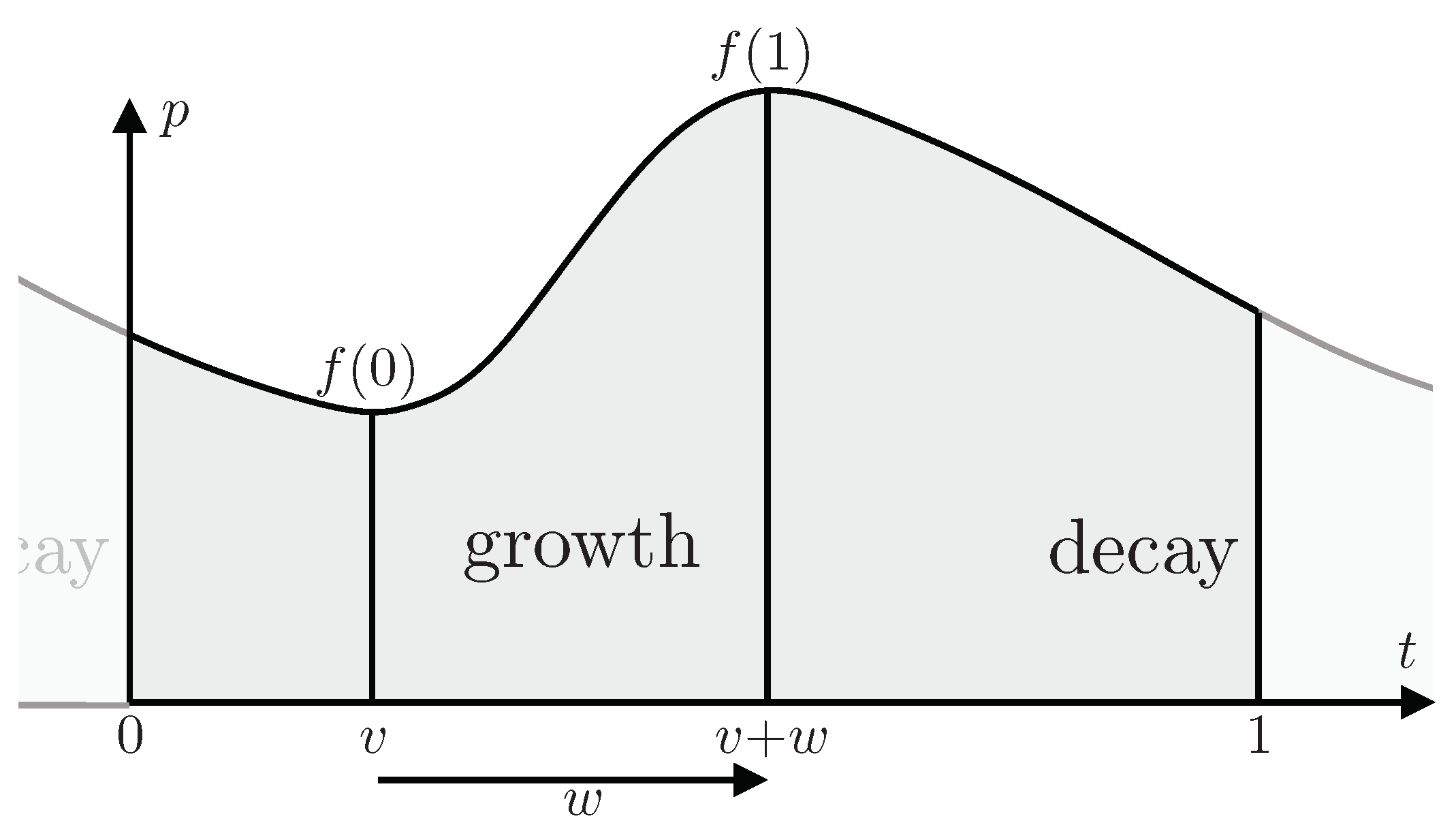
2.1. Two Parameters v and w

The $2\times 2$ information-geometry metric evaluates to

$$\left[\begin{array}{cc}{g}_{vv}& g_{vw}\\ g_{wv}& g_{ww}\end{array}\right]=\frac{1}{w(1-w)}{\int }_0^1\left[\begin{array}{cc}1& u\\ u& u^2\end{array}\right]\frac{f^{\prime }{\left(u\right)}^2}{f\left(u\right)}du=\left[\begin{array}{cc}A& B\\ B& C\end{array}\right]/w(1-w)$$

(4)

where $A,B,C$ are constants. The table shows their values for two example functions. The first is easy to integrate while the second has vanishing slope $f^{\prime }\left(0\right)=f^{\prime }\left(1\right)=0$ at the joins (as in Figure 1).

$f\left(u\right)$	$e^u/(e-1)$	$(8+6u^2-4u^3)/9$
$A$	$e-1=1.71828$	$\frac{11}{6}log2+\frac{5}{6}log5-\sqrt{15}(arctan\frac{5}{\surd 15}-arctan\frac{1}{\surd 15})=0.05945$
$B$	$1=1.00000$	$\frac{89}{12}log2-\frac{25}{12}log5-\frac{\sqrt{15}}{6}(arctan\frac{5}{\surd 15}-arctan\frac{1}{\surd 15})-\frac{4}{3}=0.02909$
$C$	$e-2=0.71828$	$\frac{251}{24}log2+\frac{5}{24}log5+\frac{13\sqrt{15}}{12}(arctan\frac{5}{\surd 15}-arctan\frac{1}{\surd 15})-\frac{31}{3}=0.01636$

The invariant volume element follows as

$$dV=\sqrt{detg}dvdw=\frac{\sqrt{AC-B^2}}{w(1-w)}dvdw$$

(5)

where, by construction, $AC-B^2>0$. The total invariant volume is infinite.

$$V={\int }_0^{1}dv{\int }_0^{1}dw\sqrt{detg}=\infty$$

(6)

2.2. One Parameter w

If v had been fixed, $\mathbf{p}$ would have been confined to a submanifold ${\mathbf{p}}_w(·)$ parameterised by w alone. The information-geometry metric reduces to

$$g_{ww}=\frac{1}{w(1-w)}{\int }_0^1{u}^2\frac{f^{\prime }{\left(u\right)}^2}{f\left(u\right)}du=\frac{C}{w(1-w)}$$

(7)

The invariant volume element follows as

$$dV=\sqrt{g_{ww}}dw={\left(\frac{C}{w(1-w)}\right)}^{1/2}dw$$

(8)

where, by construction, $C>0$. The total invariant volume is finite.

$$V={\int }_0^1\sqrt{g_{ww}}dw=\pi C^{1/2}$$

(9)

2.3. Comparison of One and Two Parameters

Both shape ((5) versus (8)) and integral ((6) versus (9)) over w differ qualitatively according to whether or not v is held fixed.

Treatment of v influences invariant volumes over w

[Geometry]

That is a mathematical fact of information geometry.

2.4. Science

For scientific application, (3) defines a wraparound translation-invariant model in which v does not affect w.

Treatment of v should not influence inference about w

[Science]

That is a science requirement. Any observational consequence of information-geometry’s invariant volumes would be rejected by the informed scientist. If there were such consequence, then observation of width w could be used to infer something about location v, contrary to the intention of the formulation.

3. Conclusions

Information geometry is not science. It denies the independence of separate parameters even though such independence is a fundamental requirement of scientific inquiry. The assumption of a geometrical connection between distributions is unnecessary for science and it fails under test.

Information geometry is a self-consistent mathematical structure which (like any other piece of mathematics) may find specialised application within science, but is not fundamental to it. The only fundamental connection is the Kullback-Leibler, which is from-to asymmetric hence not geometric.