Risk and Return Management through Smart Contract Profit Redistribution ^†

Abstract

Investing into a new product or service is a high-risk, high-return activity. This is best symbolized by the observation that the return over investment distribution of startups is a power law. Introduction of new products or services to the market might fail to generate profit even though there is a demand. Early adopters are also penalized, as they often pay a high price for something which will end up being cheaper, and might lose their warranty if the firm goes bankrupt. Innovation is slowed down. We propose to equally redistribute part of the generated profit at the end of a predefined time period to previous customers using Ethereum smart contract. Because customers are aware of the amount they would get back, their behaviors will change. The return over investment distribution and therefore the risk and return balance of the firms will also be affected. We formally define both a classic market and a market that is using our proposed system, and present an architecture to deploy such system. A preliminary numerical simulation is provided.

1. Introduction

According to a survey from the US Small Business Administration [1], only 60% of startups survive after 3 years, and 35% after 10 years. But surviving is not enough: Correlation Ventures [2] analyzed 21,640 financing between 2004 and 2013 and found that 65% had a return over investment (ROI) of 1× or less, and only 4% produced a return of 10× or more. The problem of managing risk and return has been vastly studied in finance. One of the main strategy is to have different investments whose domain performance are weakly correlated in order to lower the risk of a large loss. Another is to combine securities with different risk and return profiles. But to date there is no way to act on the expected risk and return yield by the trading activity of a single firm.

The startup’s ROI distribution is known to follow a power law. Power laws were first observed by Vilfredo Pareto when he made the empirical observation that 80% of the effects come from 20% of the causes by looking at the connection between population and wealth in 19th century Italy. Several other natural and human phenomenon are following power laws, like mass distribution of stars and frequency of words in a text. Power laws observed in the economy are the consequence of this high-risk, high-reward situation. An unequal repartition of generated wealth is undesirable for several reasons. First, it fosters wealth inequalities in the society, making the rich richer and the poor poorer. Those inequalities are aggravated by an increasing income-wealth ratio observed during the last decades [3]. A firm with a monopolly might abuse its customers by asking a high price, or make anticompetitive agreements with competitors. Power laws are also detrimental to investors and entrepreneurs. The demand as a function of the price isn’t known prior to a product’s introduction to a market. To reduce the risk, a common strategy for a firm is to first charge a high price in order to increase the probability to not lose any money. As the prospect of making profit increases, the price is decreased to attract more customers. But early adopters might be discouraged to buy if they know that the price will drop and restrain themselves. Products can be heavily affected by economies of scale effects, or the initial price might be too high even though the demand for slightly lower prices exists. In short, we might not achieve the right price, which can be defined as the one which equally maximizes the interest of all stakeholder.

We propose a way to influence the investment risk and return of a firm by equally redistributing part of the profit to past customers at the end of a specific period of time. The redistributed part of the profit is a function of the gradually increasing number of sales. Customers will be informed of both the initial price and the final price they will end up paying after the redistribution. On the other side, the ROI probabilistic distribution will change and provide a different balance of risk and return, which might be beneficial to firms. Our system is made practical by the emergence of smart contract on decentralized blockchain. Smart contracts allow for a secure execution of fund related logic, are deterministic and tamper proof, and benefit from the use of cryptocurrencies. Cryptocurrencies use cryptography to enable secure and fast transactions with a very low fee that is independent of the transaction amount. Transactions are transparent and remain accessible on the blockchain, easing bookkeeping and reducing the need for litigation and court. We developed our solution on the open source Ethereum blockchain [4] for its reliability and widespread use. In section two we formally describe both a classic market and a new market that is using our system. In section three, we provide a preliminar simulation of our system and discuss possible extensions, and in section four a smart contract architecture for the system’s deployment is described.

2. Problem Statement

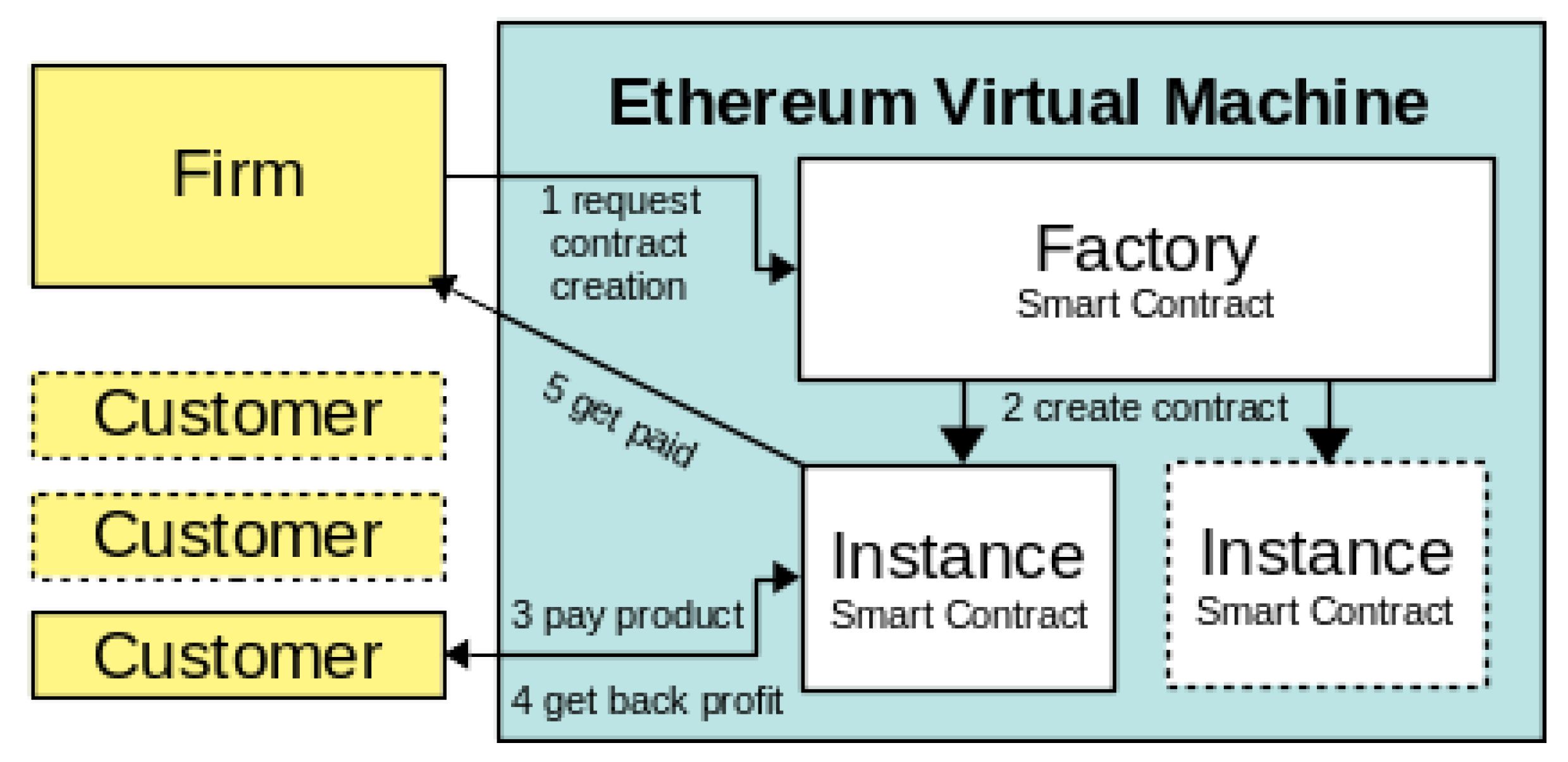
2.1. Classic Market

To distinguish expressions related to a classic market from expressions related to our proposed system, we use the subscript c, short for classic, and s, short for smart contract. We consider a firm that proposes multiple units of a single product on a market. Producing a single unit of this product has a cost $\beta$, whereas the profit ${\gamma }_c$ generated by selling a single product is a function of the price $\rho$ that is entirely decided by the firm:

$${\gamma }_c\left(\rho \right)=\rho -\beta .$$

(1)

To get its business started, the firm must invests a fixed cost $\alpha$ that includes the cost of machines, offices, research, and development. We consider for simplicity that the firm has no control over the two costs $\beta$ and $\alpha$. We can then express the quantity of sales $\widehat{n}\left(\rho \right)$ necessary for a firm to make a positive net profit as a function of the price $\rho$:

$$\widehat{n}\left(\rho \right)=⌈\frac{\alpha }{{\gamma }_c\left(\rho \right)}⌉.$$

(2)

We model the market for this product as an interaction between a set of customers $M=\{m_1,m_2,\dots ,m_N\}$ where $m_i=(t_i,h_i)$, $i\in \{1,\dots ,N\}$, and the product’s price $\rho$. A customer is interested to buy the product at a specific day $t_i\in T=\{T_1,T_2,\dots ,T_{max}\}$, but will do so only if $\rho <h_i$ at time $t_i$. The customer’s day of interest $t_i$ is drawn from a random variable I, whereas the maximum price that it is willing to pay $h_i$ is drawn from a random variable H. To model the time of interest random variable I, we use the Bass Diffusion Model [5], which describes how new products are adopted by a population through time. The Bass model is a continuous model in its original form, but a discrete approximation also exists [6]. Originally, a number of sales for a specific day t is obtained by an interaction between innovators and imitators, respectively parametrized by p and q, for a total number of customers N. In our case, we rather consider this quantity as the number of customers that are willing to buy the product at a specific day $t_i$, but will do so only if $\rho <h_i$ at time $t_i$. Parameters p and q won’t be mentionned further on: we will fix their values to the one used in Figure 1, as those values give a Bass Model that fits most observed product adoption through time.

We either can consider the subset of customers interested to buy the product for any day $t\in T$ as being drawn from M with or without replacement: wherever a customer buys the product or not the first time, will he be interested to buy it in the future again, or not ? For simplicity, we only consider customers to be drawn from the set M without replacement. Then, inspired by the Bass Model formula, we express the estimated number of customers interested to buy the product between day $t_a$ and $t_b$ using the following expression:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill N{\int }_{t_a}^{t_b}{p}_I\left(x\right)dx=N(F_I\left(t_b\right)-F_I\left(t_a\right)),\mathrm{where}{F}_I\left(x\right)=\frac{1-e^{-(p+q)x}}{1+\frac{q}{p}{e}^{-(p+q)x}}\mathrm{for}0\le x\le T_{max}.\end{array}\end{array}$$

(3)

Next, we model the probability density function $p_H\left(x\right)$ of the random variable H, whose possible outcomes represent the maximum price a customer would be willing to pay for the product, as any smooth monotonically decreasing function. $p_H\left(x\right)$ is defined between ${\rho }_{min}$, the price for which all the market potential N is captured, and ${\rho }_{max}$, the price for which no customers would buy the product. Interestingly, the demand function $d\left(\rho \right)$ for a product with price $\rho$, which describes the relationship between the price of a commodity and the quantity of that commodity that is demanded at that price, is simply equal to the market potential N times the probability density function of H:

$$d\left(\rho \right)=N·p_H\left(\rho \right),{\rho }_{min}\le \rho \le {\rho }_{max}.$$

(4)

Often simplified as a linear decreasing function, the demand-function $d\left(\rho \right)$ can also be modeled using a cumulative beta distribution function or a cumulative normal distribution function [7]. Using Equation (3), we can now express $n_c(\rho ,t,N)$ the number of sales made from the introduction of the product to the market up to day t, where $\rho$ is the price considered by the customer, with the following expression:

$$n_c(\rho ,t,N)=N{\int }_0^t{p}_I\left(x\right)dx{\int }_{{\rho }_{min}}^{\rho }{p}_H\left(x\right)dx.$$

(5)

We then get the net profit

$$f_c(\rho ,t,N)=max\{n_c(\rho ,t,N){\gamma }_c\left(\rho \right)-\alpha ,0\}$$

(6)

as a function of the price $\rho$ and the day t, and the ROI function

$${\varphi }_c(\rho ,t,N)=\frac{n_c(\rho ,t,N){\gamma }_c\left(\rho \right)}{\alpha }.$$

(7)

For simplicity, we consider that there is no competition between firms. An increasing demand for the product of a firm won’t impact the demand for the product of another. We further assume that there is no constraints on the capability of a firm to satisfy the demand, and that a product is instantaneously produced whenever needed, without the need of an inventory. Special products like Veblen goods [8], whose demand is known to increase with the price, are not taken into account.

2.2. Market with Partial Profit Redistribution

We propose to equally redistribute part of the firm’s profit to each previous customer, after day $T_{max}$, if and only if the number of sales is greater than the quantity of sales $\widehat{n}\left(\rho \right)$. We first define a new profit function ${\gamma }_s(\rho ,\zeta )$, where $\zeta$ is the percentage of the profit that is redistributed:

$${\gamma }_s(\rho ,\zeta )=(1-\zeta )\times (\rho -\beta ).$$

(8)

The redistribution will happen at time step $T_{max}$. Each additional sale made after $\widehat{n}\left(\rho \right)$ is reached will increase the final redistributed amount to each previous customer. Given the current number of sales $n_s(\rho ,t,N,\zeta )$ made by a firm since the product’s introduction to the market, it becomes possible for a customer to deterministically know how much he will receive at the end of the $T_{max}$ period. We define $\mathcal{D}(\rho ,t,N,\zeta )$ as the redistributed profit to each customer for the current number of sales $n_s(\rho ,t,N,\zeta )$ at time step t:

$$\mathcal{D}(\rho ,t,N,\zeta )=\{\begin{array}{ll}\frac{{\gamma }_s(\rho ,\zeta )\left(n_s(\rho ,t,N,\zeta )-\widehat{n}\left(\rho \right)\right)}{n_s(\rho ,t,N,\zeta )}& if{n}_s(\rho ,t,N,\zeta )>\widehat{n}\left(\rho \right)\\ 0& otherwise\end{array}$$

(9)

By taking into account the redistributed amount $\mathcal{D}(\rho ,t,N,\zeta )$ at a specific time t and the current state of the smart contract, any customer can get the price he would end up paying for the product after the redistribution of the profit at day $T_{max}$: we define this price as the instantaneous price $\overline{\rho }(\rho ,t,N,\zeta )$. It is obtained from $\mathcal{D}(\rho ,t,N,\zeta )$, and is equal to the maximum amount a customer will end up paying for the firm’s product after receiving the redistributed part of the profit:

$$\overline{\rho }(\rho ,t,N,\zeta )=\rho -\mathcal{D}(\rho ,t,N,\zeta ).$$

(10)

It should be emphasized that $\overline{\rho }(\rho ,t,N,\zeta )$ is in fact a higher bound on the final price a customer will end up paying after the redistribution, because if additional sales occur between the current day t and $T_{max}$, $\overline{\rho }(\rho ,t,N,\zeta )$ will further decrease as the redistributed part of the profit $\mathcal{D}(\rho ,t,N,\zeta )$ increases. Now, if we consider all customers to evaluate $\overline{\rho }(\rho ,t,N,\zeta )$ and not the fixed price $\rho$, then their behaviors will clearly change. Each additional sale will increase the probability of subsequent sales because $\overline{\rho }(\rho ,t,N,\zeta )$ will decrease as well, and because the price threshold density function $p_H\left(x\right)$ is a monotonically decreasing function. If we consider the number of sales made up to time step t, defined in Equation (5) with the new instantaneous price $\overline{\rho }(\rho ,t,N,\zeta )$, we get:

$$\begin{array}{c}\hfill n_s(\rho ,t,N,\zeta )=N\sum _{\widehat{t}=0}^{t-1}\left[{\int }_{\widehat{t}}^{\widehat{t}+1}{p}_I\left(x\right)dx{\int }_{{\rho }_{min}}^{\overline{\rho }(\rho ,\widehat{t}-1,N,\zeta )}{p}_H\left(x\right)dx\right].\end{array}$$

(11)

We can see that $n_s(\overline{\rho },t,N,\zeta )$ is now a recursive function that calls itself backward from time step t up to $T_0$. The new net profit function $f_s(\rho ,t,N,\zeta )$ is defined as:

$$f_s(\rho ,t,N,\zeta )=\{\begin{array}{ll}\left({\gamma }_s(\rho ,\zeta )\left(n_s(\rho ,t,N,\zeta )-\widehat{n}\left(\rho \right)\right)+{\gamma }_c\left(\rho \right)\widehat{n}\left(\rho \right)\right)-\alpha & if{n}_s(\rho ,t,N,\zeta )>\widehat{n}\left(\rho \right)\\ max\{{\gamma }_c\left(\rho \right)n_c(\rho ,t,N)-\alpha ,0\}& otherwise\end{array}$$

(12)

And the ROI function ${\varphi }_s(\rho ,t,N,\zeta )$ becomes:

$${\varphi }_s(\rho ,t,N,\zeta )=\{\begin{array}{ll}\left({\gamma }_s(\rho ,\zeta )\left(n_s(\rho ,t,N,\zeta )-\widehat{n}\left(\rho \right)\right)+{\gamma }_c\left(\rho \right)\widehat{n}\left(\rho \right)\right)/\alpha & if{n}_s(\rho ,t,N,\zeta )>\widehat{n}\left(\rho \right)\\ {\gamma }_c\left(\rho \right)n_c(\rho ,t,N)/\alpha & otherwise\end{array}$$

(13)

Because the number of potential customers N is a random variable, so is the profit function $f_s(\rho ,t,N,\zeta )$ and the ROI function ${\varphi }_s(\rho ,t,N,\zeta )$. A firm used to only have freedom over the price $\rho$ of their product. With our proposed system, a firm can now influence its risk and return by choosing the price $\rho$, the percentage of profit that is redistributed $\zeta$ and the maximum duration of the contract $T_{max}$. It is reasonable to consider that, in the proposed system, customers are evaluating the instantaneous price $\overline{\rho }(\rho ,t,N,\zeta )$ instead of the initial price $\rho$, and that in consequence their behaviors will change. Consequently, the ROI distribution ${\varphi }_s(\rho ,t,\zeta )$ of our proposed system will be different from the one of the classic market ${\varphi }_c(\rho ,t,N)$. We wish to evaluate the differences between those two probabilistic distributions, and see how the parameters chosen by a firm will influence them. First, we wish to see if a the market that is using our system can reduce the percentage of firms that are losing money after $T_{max}$, compare to a classic market. Namely:

$$P[0\le {\Phi }_s<1]<P[0\le {\Phi }_c<1].$$

(14)

where the ROI random variables ${\Phi }_s$ and ${\Phi }_c$ are respectively defined as

$${\Phi }_s={\int }_{t=0}^{T_{max}}{\varphi }_s(\rho ,t,N,\zeta )dt,\mathrm{and}{\Phi }_c={\int }_{t=0}^{T_{max}}{\varphi }_c(\rho ,t,N)dt.$$

(15)

Second, we wish to quantify the reduction of the percentage of firm that made a profit higher that a specific threshold $\theta$:

$$P[{\Phi }_c>\theta ]>P[{\Phi }_s>\theta ].$$

(16)

3. Preliminary Simulation

Due to the large number of variables, simulating the proposed system is challenging. We need to find a satisfactory balance between accuracy of the simulation with regard to reality, which increases the number of variables and therefore the complexity, and feasibility, where we must agree on a set of assumptions and simplifications. We sample our market’s parameters from a set of probabilistic distributions that we believe to represent the reality of a market, based on common sense and available economic knowledge. However we acknowledge that the choice of those probabilistic distributions is arbitrary and might not be best. First, we fix the probability distribution ${\varphi }_c$ of the ROI random variable ${\Phi }_c$ after 365 days to be a power law of the form

$$f\left(x\right)=N{x}^{-k}.$$

(17)

where N, the market’s potential, is fixed to 10,000 and the exponent k to $0.047$. The exponent is selected such that $P_{365}[{\Phi }_c<1]$, i.e. the probability for a company to lose money after one year is equal to 65%, a proportion that is observed in the real world according to [2]. We randomly sample this distribution with 10,000 points. We then sample ${\rho }_{min}$ and ${\rho }_{max}$ from two gaussian distributions, as well as the price $\rho$ from a uniform distribution between ${\rho }_{min}$ and ${\rho }_{max}$. The demand for the price $\rho$ is obtained using a linear demand function defined between ${\rho }_{min}$ and ${\rho }_{max}$. The production cost of a single unit is sampled from a beta distribution with the constraint that $\beta <\rho$ if and only if ${\varphi }_c>0$. Finally, the investment cost $\alpha$, the last unknown parameter, is deduced using Equation (7). The parameters of the generated dataset are displayed in

Table 1. Dataset parameters.

Demand Function	N	Maximum $\mathit{\alpha }$	${\mathit{\rho }}_{\mathbf{min}}$	${\mathit{\rho }}_{\mathbf{max}}$	$\mathit{\beta }$	Power Law k
Linear	10,000	10,000,000	$\mathcal{N}(20,1000)$	$\mathcal{N}$(500, 10,000)	$0.2$	$0.047$

. We obtain a set of simulated datapoints that we consider to be i.i.d sampled from a real world market. We then simulate a scenario where each product represented by a datapoint is proposed on the market using our proposed system. We can see in Figure 2 that the return over investment distribution is compressed toward the left-hand side of the x axis as the redistributed percentage $\zeta$ grows.

In this work, we assumed the demand function to be linear, but monotonically decreasing non-linear functions, like cumulative beta distributions or cumulative normal distributions, are said to better represent observed demand function in the market [7]. Further simulations are needed to investigate the effect of those functions on the proposed system, and see if it could help to decrease $P_{365}[{\Phi }_s<1]$. Furthermore, we believe that there is much potential in having the redistributed profit percentage $\zeta$ to be a function of the current ROI ${\Phi }_s(\rho ,t,N,\zeta )$. For example, the redistributed percentage could increase proportionally to the current ROI at time step t if the current ROI is above a specific threshold, and then stay constant if the ROI goes above another threshold.

4. Smart Contract Implementation

A proof of concept was created on the Rinkeby testnet of the Ethereum network, where ETH coins do not have value. The smart contract source code is currently being reviewed thoroughly, and will soon be shared with the community. A factory pattern was used [9], where one smart contract has the responsibility to create specific instances of our redistribution system. Any firm that is willing to use our system can ask this factory smart contract to create a specific instance for their product using their own parameters. This pattern has several benefits. Any smart contract whose logic is managing money in the form of ETH, the native Ethereum cryptocurrency, opens the way to potential misconceptions which can cause the loss of all fund managed by this smart contract. Therefore, a smart contract should be deeply understood and analyzed by security and blockchain expert to avoid failures after deployment. A factory pattern concentrates the responsability in the hand of the one who deployed the factory smart contract. This design pattern ensures the correctness of all created instance smart contract, and allows for the verification of the firm’s input parameters. It also alleviates the need for a firm to understand the technical details of the blockchain platform in order to focus on the provided functionalities. Figure 3 provides an example of a factory architecture.

5. Conclusions

We formally described a system to influence the ROI probability distribution of any trading activity where products or services are sold by one to many. Our system equally redistributes part of the generated profit to previous customers at the end of a predefined time period. By considering the price they would end up paying and not the current price, we showed that customers would influence the ROI distribution, and therefore the risk and return balance. A preliminary simulation was conducted. While in its current form the proposed system successfully redistribute part of the generated profit to every previous customer, further research and experimentation are needed to lower the probability for a firm to lose money. To achieve this goal, possible extensions to this work were presented.