Blast Wave Assessment in a Compound Survival Container: Small-Scale Testing †
Abstract
:1. Introduction
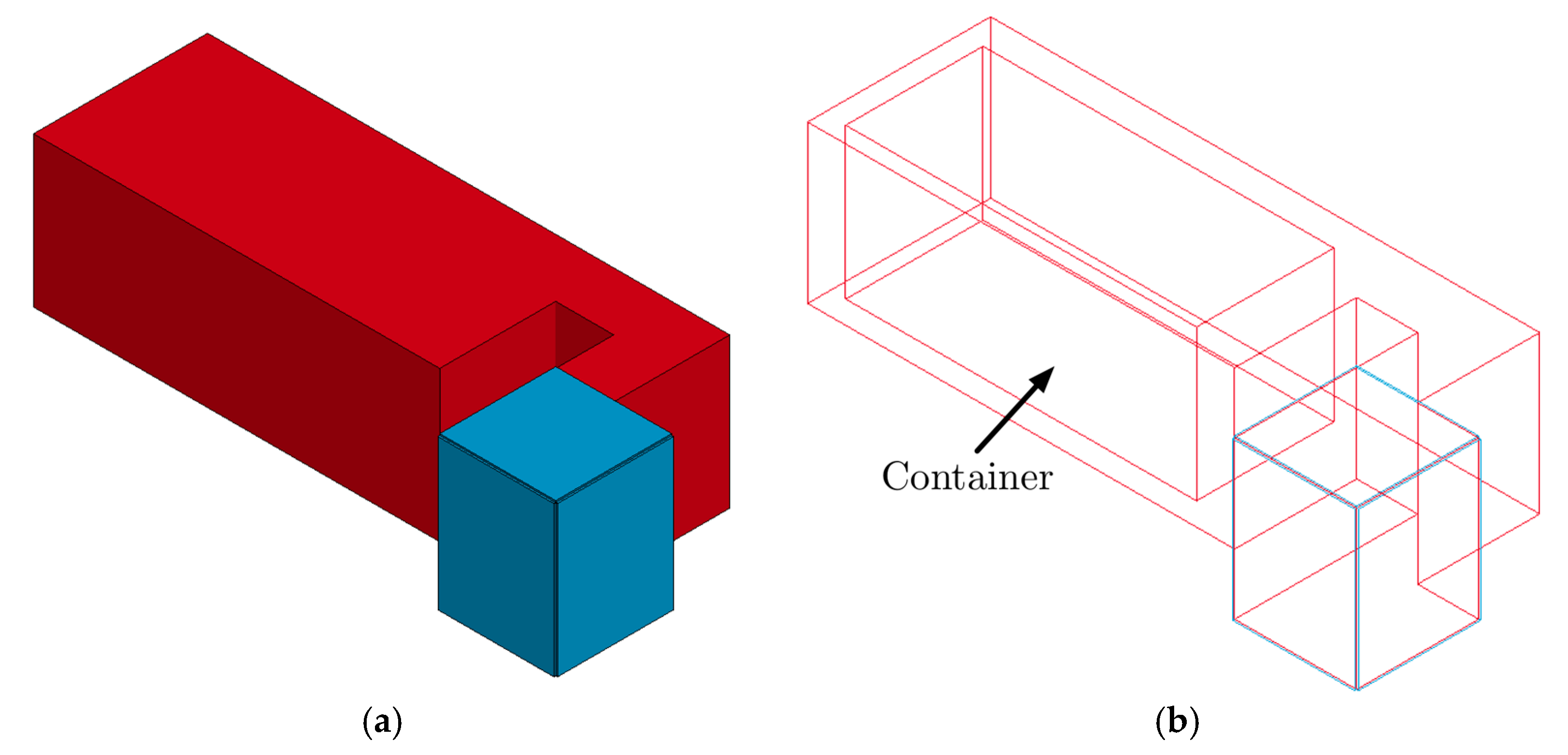
2. Experimental Set-Up
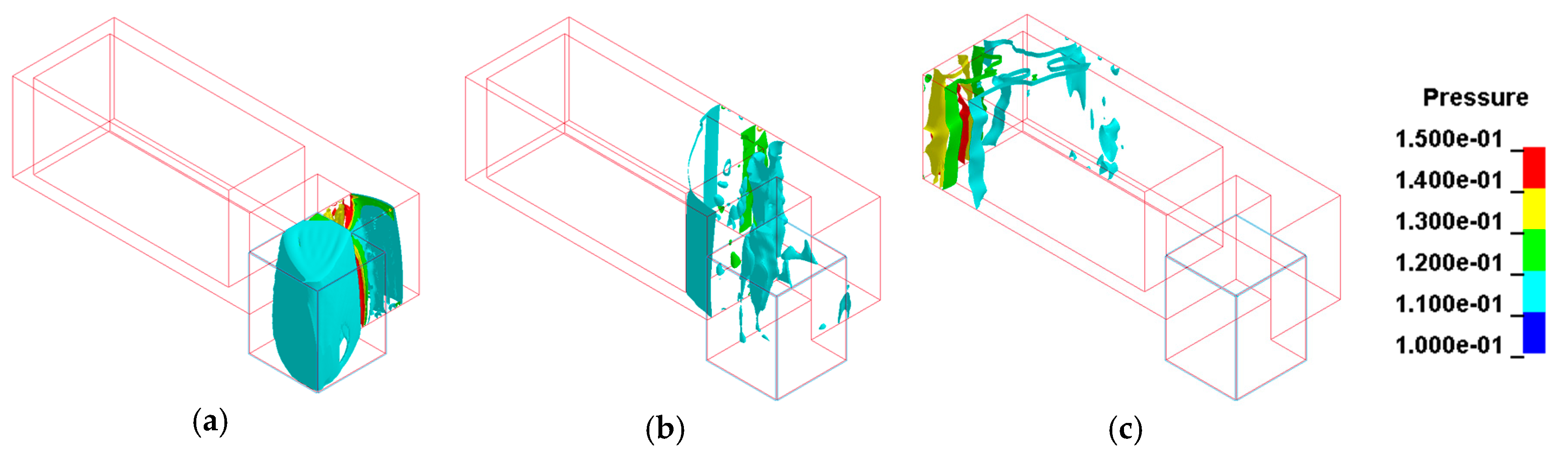
3. Numerical Modelling
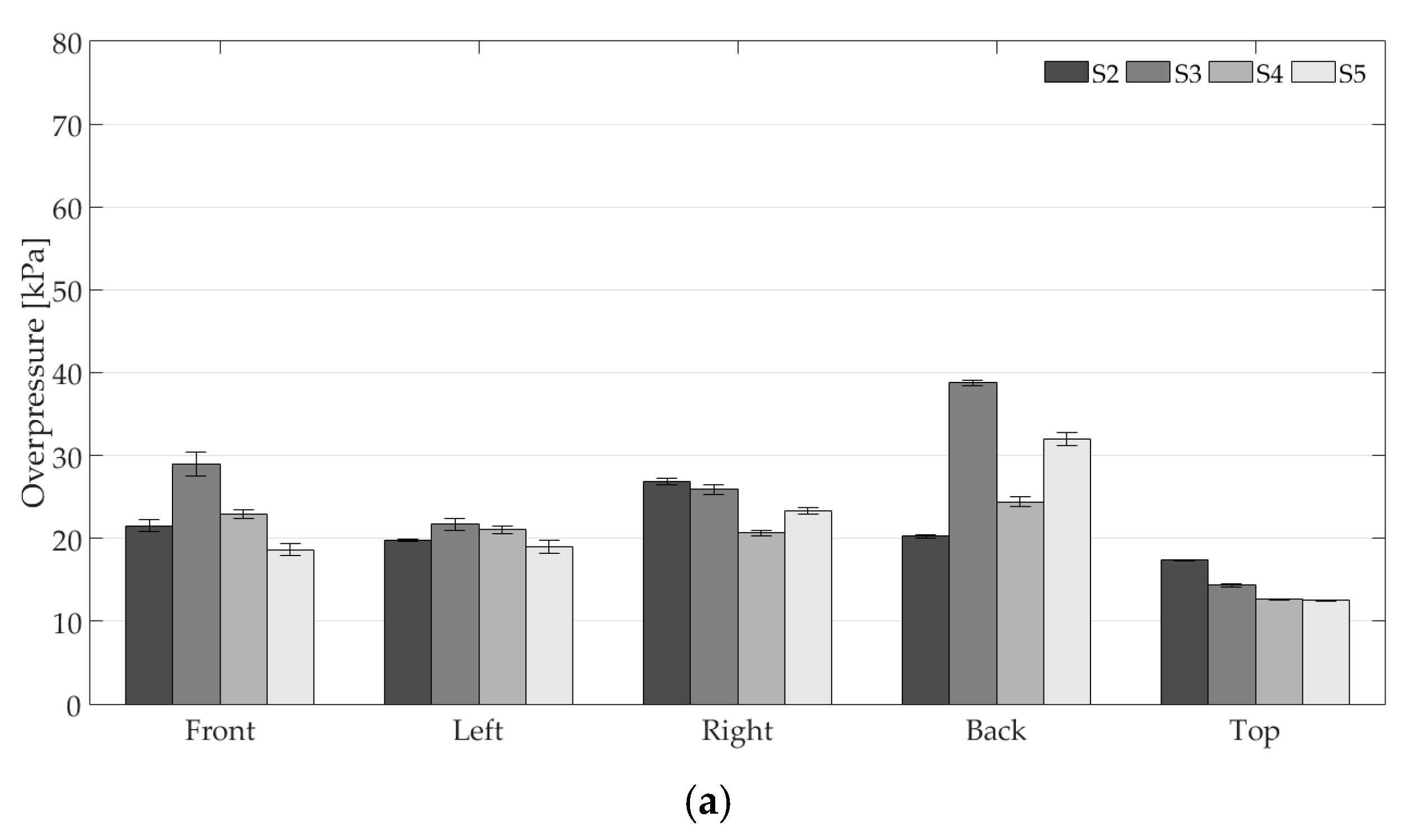
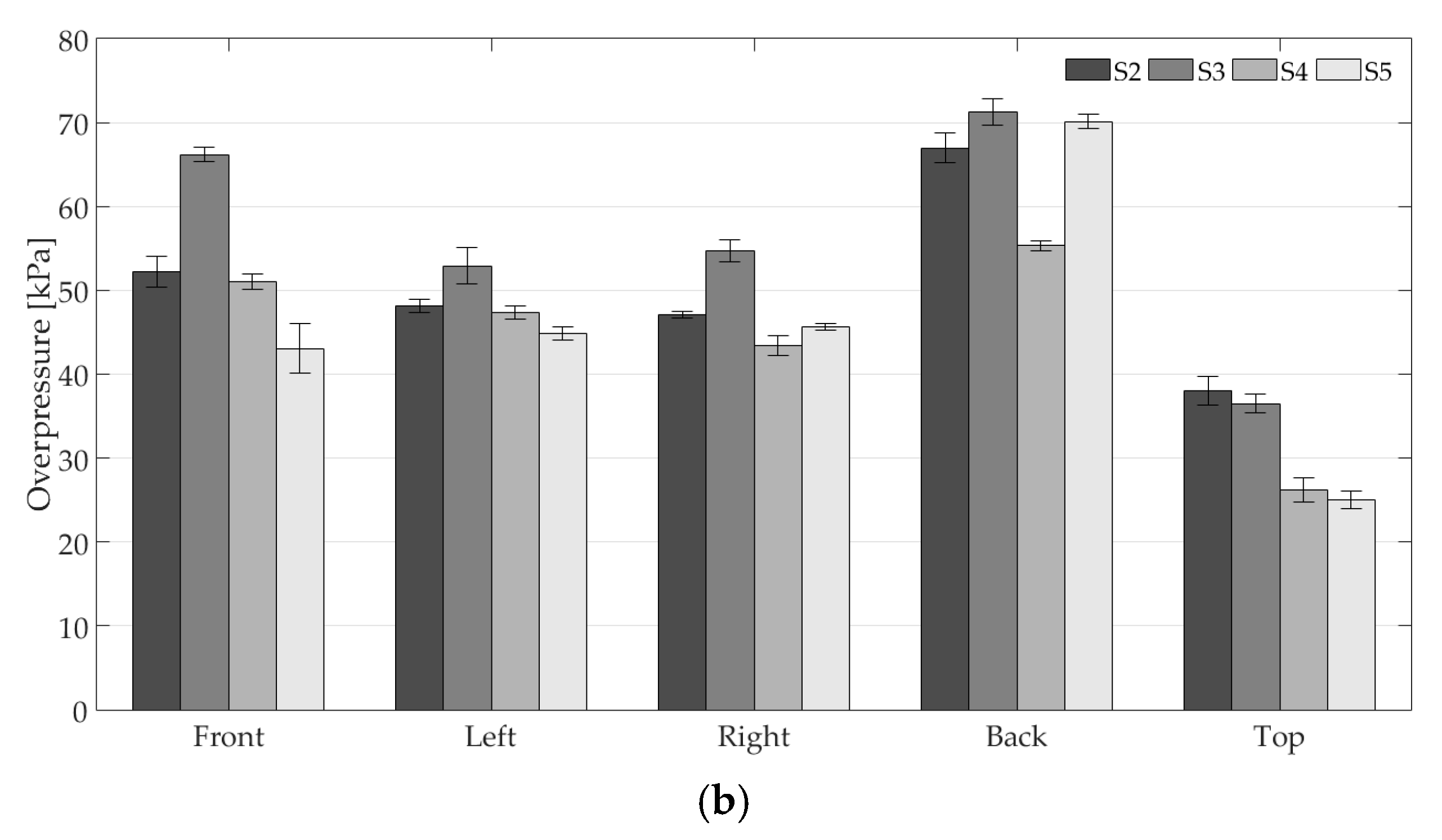
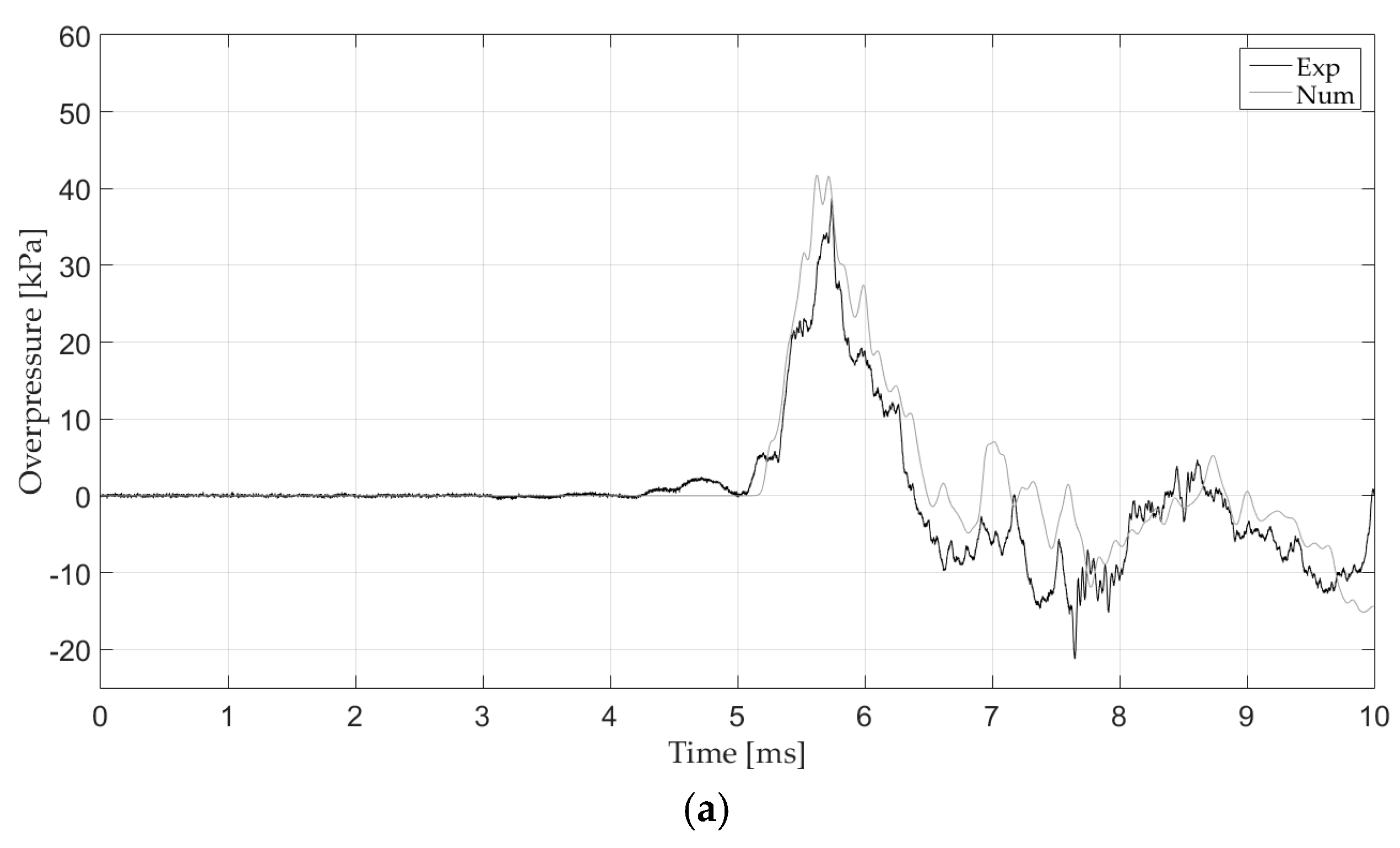
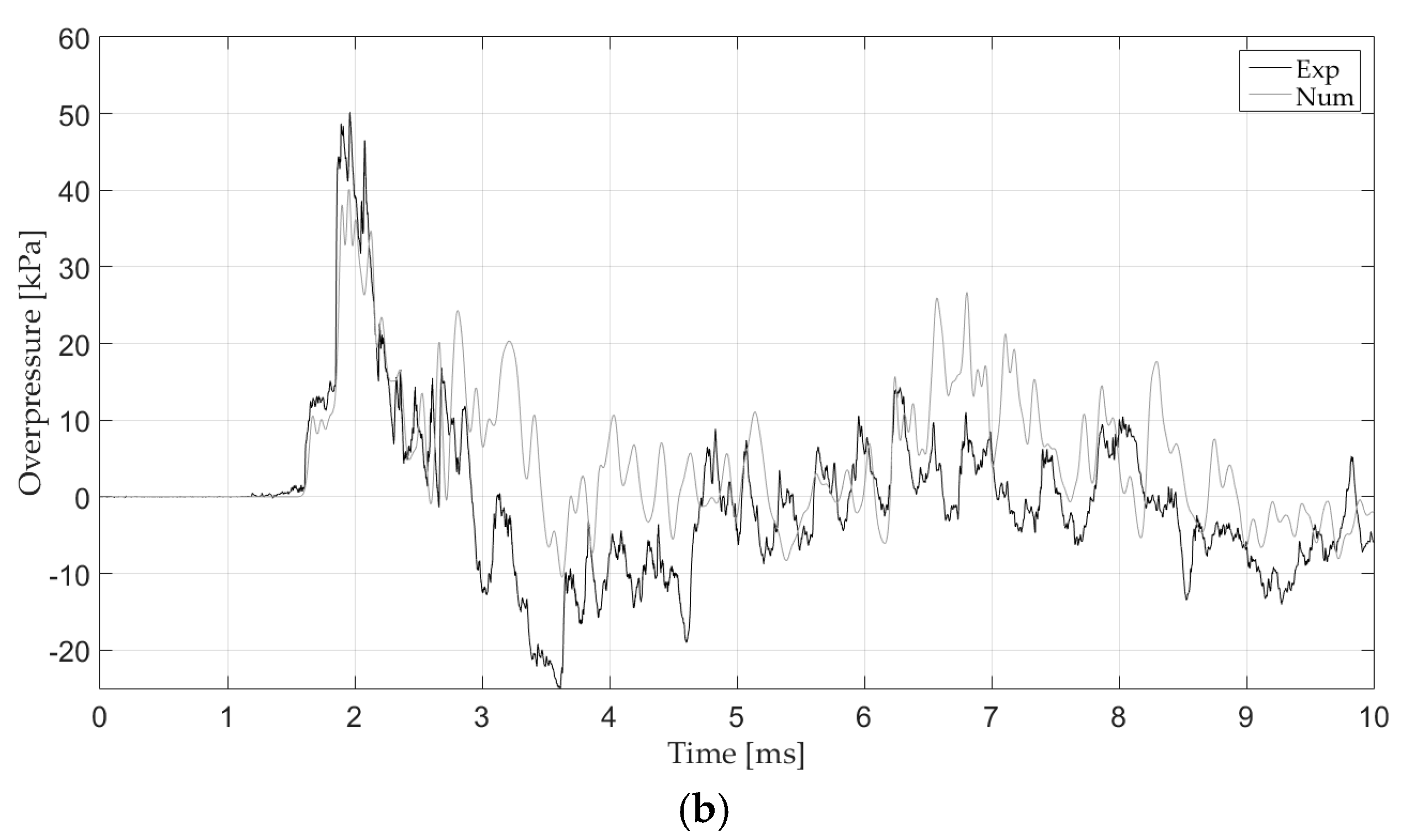
4. Results and Discussion
5. Conclusions
Acknowledgments
References
- Smith, P.D.; Hetherington, J.G. Blast and Ballistic Loading of Structures; Butterworth-Heinemann: Oxford, UK, 1994. [Google Scholar]
- Rigas, F.; Sklavounos, S. Experimentally validated 3-D simulation of shock waves generated by dense explosives in confined complex geometries. J. Hazard. Mater. 2005, A121, 23–30. [Google Scholar] [CrossRef] [PubMed]
- Sauvan, P.E.; Sochet, I.; Trélat, S. Analysis of reflected blast wave pressure profiles in a confined room. Shock Waves 2012, 22, 253–264. [Google Scholar] [CrossRef]
- Lecompte, D.; De Schepper, R.; Belkassem, B.; Kakogiannis, D.; Reymen, B.; Vantomme, J. A modular building-block system for lab-scale explosive testing of urban type configurations. In Proceedings of the 23rd Military Aspects of Blast and Shock, Oxford, UK, 7–12 September 2014. [Google Scholar]
- Baker, W.E.; Cox, P.A.; Westine, P.S.; Kulesz, J.J.; Strehlow, R.A. Explosion Hazards and Evaluation; Elsevier Science: Amsterdam, The Netherlands, 1983. [Google Scholar]
- U. S. Department of the Army. Fundamentals of Protective Design for Conventional Weapons; Technical manual (TM5-855-1); U.S. Department of the Army: Washington, DC, USA, 1986. [Google Scholar]
- Slavik, T.P. A coupling of empirical explosive blast loads to ALE air domains in Ls-Dyna. In Proceedings of the 7th European LS-DYNA Conference, Salzburg, Austria, 14–15 May 2009. [Google Scholar]
- Ousji, H.; Belkassem, B.; Louar, M.A.; Kakogiannis, D.; Reymen, B.; Pyl, L.; Vantomme, J. Parametric study of an explosive-driven shock tube as blast loading tool. Exp. Tech. 2015, 40, 1307–1325. [Google Scholar] [CrossRef]


| Material | Parameter | Value |
|---|---|---|
| Density | 1.225 kg/m3 | |
| Air | C0 = C1 = C2 = C3 = C6 C4 = C5 Specific internal energy | 0 0.4 2.5 × 10−4 kJ/kg |
| SOFF (m) | Faces of Container | Mean | Standard Deviation |
|---|---|---|---|
| Front | 23.01 | 3.75 | |
| 1 | Left Right Back Top | 20.37 24.16 28.85 14.21 | 1.05 2.41 7.10 1.97 |
| 0.5 | Front Left Right Back Top | 52.12 48.35 47.71 65.91 31.45 | 8.34 2.91 4.25 6.31 5.87 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caçoilo, A.; Mourão, R.; Belkassem, B.; Teixeira-Dias, F.; Vantomme, J.; Lecompte, D. Blast Wave Assessment in a Compound Survival Container: Small-Scale Testing. Proceedings 2018, 2, 540. https://doi.org/10.3390/ICEM18-05459
Caçoilo A, Mourão R, Belkassem B, Teixeira-Dias F, Vantomme J, Lecompte D. Blast Wave Assessment in a Compound Survival Container: Small-Scale Testing. Proceedings. 2018; 2(8):540. https://doi.org/10.3390/ICEM18-05459
Chicago/Turabian StyleCaçoilo, A., R. Mourão, B. Belkassem, F. Teixeira-Dias, J. Vantomme, and D. Lecompte. 2018. "Blast Wave Assessment in a Compound Survival Container: Small-Scale Testing" Proceedings 2, no. 8: 540. https://doi.org/10.3390/ICEM18-05459
APA StyleCaçoilo, A., Mourão, R., Belkassem, B., Teixeira-Dias, F., Vantomme, J., & Lecompte, D. (2018). Blast Wave Assessment in a Compound Survival Container: Small-Scale Testing. Proceedings, 2(8), 540. https://doi.org/10.3390/ICEM18-05459






