Abstract
In modal identification, the value of the model parameters and the associated uncertainty depends on the quality of the measurements. The maximum likelihood estimator () is a consistent and efficient estimator. This means that the value of the parameters trends asymptotically close to the true value, while the variance of such parameters is the lowest possible with the associated data. The implementation and application can be complex and generally need strong computational requirements. In applications where the number of inputs and outputs are elevated (as in modal analysis) is common to reduce the covariance matrix to a diagonal one where only the variances are considered. This implementation is still consistent but not efficient. However, it generates acceptable results. The current work shows that using efficiently the output information as complement to the input–output relations, it is possible to improve the model identification reaching similar levels than the , while reducing the execution time and the computational load.
1. Introduction
The input-output (transfer function relation) frequency domain approach requires the direct measurement of the input–output signals. In some applications such measurements, specially the inputs of the system, are difficult to assess, and/or in addition to the applied excitation other/others unknown sources can go into the system generating correlations in the variables. The previous scenario is common in modal analysis with the additional factor that the number of outputs can easily reach hundreds, even thousands.
An estimator that has the desired properties of consistency and efficiency is the maximum likelihood (mle) estimator. This is, the value of the parameters trends asymptotically close to the true parameter value (consistency), while the variance of such parameters is the lower possible with the associated data (efficiency) [1,2]. The implementation of this estimator could be complex since it requires the estimation of the covariance matrix. This is an important issue since when the number of variables is high (as in modal analysis) this requires the development of high amount of experiments. In many cases, in order to reduce the number of experiments and the computational processing time, the covariance matrix is reduced to a diagonal one where only the variances are present. This implementation (called here diagonal implementation of the mle ()) still generates a consistent estimation but the efficiency lost (it is not possible to reach the lower variance in the model and parameters associated with the used data), however the result are quite acceptable [2,3].
In the present work, in a similar way as in the where the covariance matrix is reduced to a diagonal one, two estimators are introduced. But in addition to the input–output relations, the output–output relations are used as complement to the input–output information. Similar to a traditional input–output transfer functions the output–output functions are defined as the frequency-domain ratio between two outputs, and describes the relative admittance between two measurements. The output–output relations are interpreted as the response data normalized by a reference response instead of by the input excitation [4,5]. Unlike the transfer function, these functions are independent of the input information and its associated noise [3].
The article starts describing the estimator, subsequently introduces the followed by the approaches considering the only output relations. The comparison between the different estimators is presented by mean of a Monte-Carlo simulation examples. The different estimators are assessed based on the global uncertainty reached by the estimators and the computational execution time. Finally the conclusions are presented.
2. Maximum Likelihood Estimator ()
The parametric transfer function considered here is scalar matrix description or common denominator transfer function described as
but can be extended to left and right matrix fraction description models. In (1) is a q-output by p-input polynomial matrix. is q-output by one vector and is p-input by one vector. The locations of the matrix are given by while the denominator is given by . The index and refer to the order of the polynomials and respectively.
Assuming that the noise on the real and imaginary part of the spectra of the input and output signals are independent, zero mean, Gaussian random variables, it can be proven [1] that the of the parameters is found by minimizing the cost function
with H the complex conjugate transport operation and
The matrix is the inverse of the covariance matrix
with the covariance matrices of the perturbation noise of the inputs and outputs at the frequency lines k. The perturbation noise can be determined from a priori measurements [6].
Diagonal Implementation of the Estimator ()
The mle estimator is optimum since it follows the properties of consistency and efficiency and converge to the noiseless solution [2]. However, the procedure requires to estimate the covariance matrix and its inverse (4). which, carries a significant experimental time consumption and computation load. To reduce the computational load it is possible to assume independence between the inputs and outputs. In this sense the covariance matrix (4) becomes a diagonal matrix and from here a fast and practical implementation is achieved [7].
3. Extension of Diagonal- Using Output-Output Relations ()
The equation error (3) considers the input-output relation and from here its dependency of the input signal and related noise. However, along the output–output relations this dependency is set aside.
Output–output relations are obtained by the ratio of two response spectra. This is, the ratio between the output q and r is . From (1) the output-output equations are reduced to:
with and the numerator polynomials occurring in the transfer function and . Observe that the input excitation signal is eliminated by taking the ratio between the response-output spectra.
The equation error is extended to the output-output equations as:
and the covariance matrix became
with T the matrix of the numerator relations.
The solution of (2) requires the inverse of (7) which is a singular matrix since there exist linear dependency between the rows. However, as in the , it is assumed that covariance matrix is diagonal, or in other words it is assumed that the noise is uncorrelated between the inputs and outputs, and that the contribution of the non-diagonal terms are irrelevant. The covariance matrix (7) becomes diagonal and includes the input–output and output–output relations and allow a fast implementation. This implementation will provide consistent estimators although non efficient. However, the estimation using the output–output relation will provide better results in terms of efficiency than the common implementation.
4. Diagonal Implementation of the Using Orthogonal Equations ()
The dimension of the output–output equations is function of the number of outputs. In fact it is the combination without repetition of q-outputs taken 2 at a time. This combination can easily reach considerable values for few number of variables. For example: for a system with 10 outputs the number of output–output equations is already 45, for 100 the number of equations reach 4950 and for more of 200 outputs the number exceed the twenty thousand!
A generalization to the output–output equations that keep the number of relation in similar proportion to the number of input-output equations is achieved by taken the orthogonal value of the numerator such that the effect of the input (and associated noise) is eliminated from the equations. This is, from the input-output relation (1) by left multiplication at both sides of the equation by the orthogonal value of the numerator () we have
observe that the effect of the input and associated noise has been removed from the equation.
Similar to the previous section the equation error and associated covariance have the shape of (6) and (7) respectively, but the explicit outpu–output relations is substituted by the general form . Here again assuming that the variables are independent taking only the information of the diagonal, the cost function (2) can be implemented.
5. Experiment
Four different estimators , , and are compared in a system under two scenarios: The first scenario presents uncorrelated independent noise added at the inputs and outputs of the system with levels that reach signal to noise ratios (SNR) of 70, 50, 40, 30, 20, 15 and 10 dB. The second scenario covers the conditions of the first one, but includes the presence of an unknown excitation. The unknown excitation reach attenuations (regarding the known excitation) of −50 and −10 dB. Table 1 summarizes the employed levels while the Figure 1 illustrates the experimented scenarios. The different estimators will be assessed by mean of the general variance (GV) of the parameters of the system (the GV can be seen as a scalar measure of the overall multidimensional scatter of the analyzed data. Lower the GV value is, lower variance in the parameters) and the computational execution time.

Table 1.
SNR and attenuation levels used for the input, output and unknown excitation.

Figure 1.
Experimental scenarios. (a) This scenario only includes the presence of uncorrelated independent noise at the inputs and outputs; (b) This scenario includes the presence of uncorrelated independent noise at the inputs and outputs and presence of unknown forces acting on the system.
6. Results
1st Scenario: Independent and Uncorrelated Noise. In this scenario only independent and uncorrelated noise are present at the inputs and outputs of the system. The Figure 2 shows the general variance on the parameters for the different estimators (Figure 2a) and the execution time (Figure 2b). For low levels of noise at the input the estimators generate similar results. However, when the SNR of the input becomes lower (high presence of noise) and the SNR at the outputs grow, the estimators using complementary output equations ( and ) show better results than the estimator. In fact the results of the and are superimposed on the results.
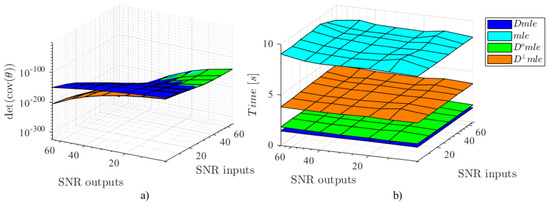
Figure 2.
Results of the , , and estimators when only independent and uncorrelated noise is present at the input and output of the system. (a) General variance; (b) mean execution time.
The mean execution time for the different estimators is shown in the Figure 2b. According with the results, the estimator requires less time while the estimator expend at least one order of magnitude more. The and the estimators present execution times lower than the half required for the being lower for the estimator where the output–output relations are explicit.
2nd Scenario: Independent Uncorrelated and Correlated Noise. Similar than the first scenario uncorrelated noise has been added into the inputs and outputs of the system, but in addition, one unknown excitation is set, which will generate correlated noise in the system. The result shows, as in the previous case, that at high levels of noise at the input, the outputs relations improve the identification of the system reducing the associated variance when is compared with the implementation. The unknown excitation generate add correlation in the variables so that the and the move away of the results. But in any case these estimators still present better performance, in general variance terms, than the . See Figure 3. The execution time show similar results as in the first scenario: The implementation shows the lowest time consumption, the estimator the highest and the proposed methods, and , show intermedian execution times. See Figure 4.
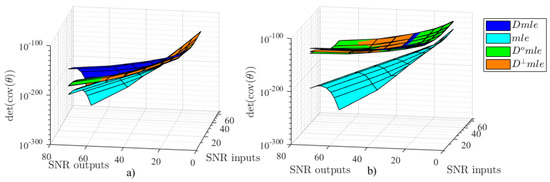
Figure 3.
General Variance of the , , and estimators when an unknown excitation is present. The unknown attenuation excitation regarding the known excitation is: (a) −50 dB; (b) −10 dB.
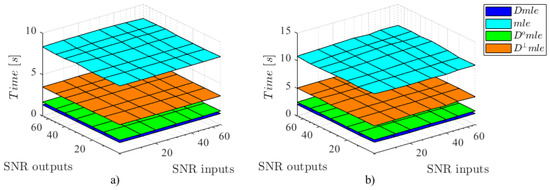
Figure 4.
Mean execution time of the , , and estimators when an unknown excitation is present. The unknown attenuation excitation regarding the known excitation is: (a) −50 dB; (b) −10 dB.
7. Conclusions
The properties of consistency and efficiency of the estimator makes it the best choice in the identification of a system. However, the practical implementation of this estimator is complex since requires the estimation and inverse calculation of the covariance matrix. The diagonal implementation of the estimator () reduces the number of required experiments as well as the computation requirements and execution time. The price to pay for this simplified and faster implementation is the lost of the estimator’s efficiency. In order to improve the results of the estimator, the article propose to use conveniently the output information. The estimator uses explicitly all the possible combinations of output–output relations, while the uses the orthogonal projection of the numerator. The proposed methods improve the results since the covariance of the model become closest to the results, specially in the case where the input signal is highly contaminated by noise.
Author Contributions
P.G. and O.O. conceived and design the proposed estimators, wrote the paper, develop the softwatre implementation of the algorithms, proposse de experiments and analyzed the data. M.E.-K. orientate the data analysis and orientate the software implementation.
Acknowledgments
This work is financially supported by SRP-OPTIMech Vrije Universiteit Brussels (VUB).
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Guillaume, P.; Pintelon, R.; Schoukens, J. Description of a parametric maximum likelihood estimator in the frequency domain for multi-input, multi-output systems and its application to flight flutter analysis. Mech. Syst. Signal Process. 1990, 4, 405–416. [Google Scholar] [CrossRef]
- Pintelon, R.; Schoukens, J. System Identification: A Frequency Domain Approach; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Olarte Rodriguez, O.; Guillaume, P. Improving Modal Parameter Estimation by Complementary Output–Output Relations. In Topics in Modal Analysis & Testing; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Weijtjens, W.; De Sitter, G.; Devriendt, C.; Guillaume, P. Operational Modal Parameter Estimation of MIMO Systems Using Transmissibility Functions. Automatica 2014, 50, 559–564. [Google Scholar] [CrossRef]
- Devriendt, C.; Steenackers, G.; Sitter, G.D.; Guillaume, P. From operating deflection shapes towards mode shapes using transmissibility measurements. Mech. Syst. Signal Process. 2010, 24, 665–677. [Google Scholar] [CrossRef]
- Schoukens, J.; Pintelon, R.; Renneboog, J. A maximum likelihood estimator for linear and nonlinear systems—A practical application of estimation techniques in measurement problems. IEEE Trans. Instrum. Meas. 1988, 37, 10–17. [Google Scholar] [CrossRef]
- Guillaume, P.; Verboven, P.; Vanlanduit, S. Frequency-domain maximum likelihood identification of modal parameters with confidence intervals. In Proceedings of the 23rd International Seminar on Modal Analysis, Leuven, Belgium, 16–18 September 1998; pp. 359–366. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).