Mechanoluminescent Materials: A New Way to Analyze Stress by Light ^†

Abstract

The monitoring of stress changes in structural components under various kinds of dynamical loading is crucial for the assessment of their integrity and lifetime. In addition to many methodologies available, such as strain gauges, optical fiber sensors, X-Ray diffraction and digital image correlation, we introduce a novel non-contact method to visualize stress distributions based on mechanoluminescence (ML). ML is a phenomenon occurring in some materials that emit light upon an applied stress level. In this paper, we develop the ML material (Ca_0.4Sr_0.6)Al₂Si₂O₈:1%Eu²⁺,1%Ho³⁺, a glow-in-the-dark material, to visualize stress distribution in a disc, as well as the stress field of an ultrasonic transducer. The properties of defects in the ML phosphors, which are responsible for ML in this material, are vital for stress visualization.

1. Introduction

Structural components undergo a variety of dynamic loading conditions during their operating life. The monitoring of mechanical stresses induced by such loading is vital for the assessment of the components’ structural integrity [1]. Large and abrupt stress changes and stress concentrations can in fact be responsible for the onset of micro-cracks in the component and may drastically decrease its residual strength as well as life expectancy. Many techniques for stress monitoring are available, using both contact and non-contact sensing devices and methodologies. The use of strain gauges is very common and accessible for many applications, requiring simple wiring. Another contact method is to use Fiber Bragg Grating (FBG) sensors, which shift the wavelength of reflected light as the fibers are strained [2]. Non-contact techniques for measuring stress distribution are also available. Digital image correlation is a popular one, but it requires relatively expensive setups [3]. Photoelasticity also plays a role in visualizing stress distributions, because the difference of maximum principal stress and minimum principal stress is proportional to the isochromatic value [4]. It is applicable to complex geometry, but is limited to transparent objects and polarized light is required.

Mechanoluminescence comes in here as an alternative route to visualize stress distribution. ML materials are special phosphors which can emit light when subjected to mechanical loads. The intensity of the emitted light is directly linked to the intensity of the stress field, which can therefore be determined by measuring and adequately processing the ML phenomenon [5]. Interestingly, it is also possible to visualize the stress fields introduced by other excitation sources, such as inverse piezoelectricity, magnetorestriction and ultrasound irradiation. This has expanded the application range of ML [6]. Although many different phosphors can be readily prepared by doping transparent crystals with luminescent ions, the number of nondestructive ML phosphors is still below 100, which limits the tuning of desired properties such as emission color, sensitivity to load, afterglow, etc. [6]. To optimize the ML effect for certain applications, engineering and tailoring of ML phosphors are crucial. In this paper we report the anorthite (Ca_0.4Sr_0.6)Al₂Si₂O₈:1%Eu²⁺,1%Ho³⁺ ML material, which is responsive to both mechanical loading and ultrasonic stimulation. We show that the inclusion of Ho³⁺ improves the ML intensity and that the concentration of defects and their energy position with respect to that of the pure host crystals are very important for tuning the ML properties.

2. Materials and Methods

ML materials ZnS:1%Mn²⁺, (Ca_0.4Sr_0.6)Al₂Si₂O₈:1%Eu²⁺ and (Ca_0.4Sr_0.6)Al₂Si₂O₈:1%Eu²⁺,1%Ho³⁺ were prepared by a solid-state reaction method, i.e., sintering the starting materials under a high temperature. Starting materials were weighted and ground in an agate mortar for 10 min and then were pressed into discs of 16 mm diameter. Those discs were placed in a corundum crucible, which was then placed in a horizontal tube furnace and heated at 1050 °C for 3 h under a gas flow of N₂ (flow rate 60 mL/min) for ZnS:1%Mn²⁺, and at 1350 °C for 6 h under 95%N₂-5%H₂ (flow rate 140 mL/min) for (Ca_0.4Sr_0.6)Al₂Si₂O₈:1%Eu²⁺ and (Ca_0.4Sr_0.6)Al₂Si₂O₈:1%Eu²⁺,1%Ho³⁺. After cooling down to room temperature, the discs were crushed and ground into fine powders for further characterization.

The emission and excitation spectra were collected with an Edinburg Instrument FS920 spectrometer at room temperature. For thermoluminescence measurements, the phosphor powders were pressed into small discs of roughly 5 mm diameter. The disc was placed on a heating stage in a vacuum chamber. After being excited by UV light of 370 nm from a LED (for (Ca_0.4Sr_0.6)Al₂Si₂O₈:1%Eu²⁺,1%Ho³⁺) or of 300 nm from a Xenon lamp (for ZnS:1%Mn) for 10 min, the disc was cooled down to −60 °C and then heated up to 225 °C with a fixed rate of 0.5 K/s. The luminescence was detected with a calibrated photometer ILT1700, and corrected for thermal quenching (i.e., the steady state photoluminescence intensity as a function of temperature).

For the stress visualization, coupons (length > 120 mm, width 12.5 mm, thickness 2.0 mm) were prepared by the resin transfer molding method. Resin (Epikote™ Resin MGS LR 135) and hardener (Epikote™ Resin MGS LR 137) were taken in a 10:3 weight ratio and mixed by stirring together with ML powders (weight ratio 3%). Then they were infused through a mold, cured at room temperature for 24 h, post-cured at 85 °C for 15 h and then cooled down to room temperature for demolding. These coupons were then placed inside an Instron ElectroPuls E10000 apparatus for tensile tests. After being illuminated by UV light (365 nm) for 150 s, each coupon was left unloaded for a period to allow the fading of the strong afterglow. Then a linear tensile load was applied, and the maximum load was held for at least 200 s before being released. The light emission was collected with a photomultiplier tube (Hamamatsu^® H10722-210) and synchronized with displacement and force signals via a National Instrument^® data acquisition unit (NI 9234) with a sampling rate of 2048 Hz.

Besides these coupons, a disc (diameter 25 mm, thickness 10 mm) of epoxy resin (Struers^® Epofix^®) mixed with ~0.3 g (Ca_0.4Sr_0.6)Al₂Si₂O₈:1%Eu²⁺,1%Ho³⁺ was compressed using a hydraulic machine (AC Hydraulic^TM) while the ML was recorded with an CMOS camera (Ximea^® MC031MG). The ultrasonic field was also visualized by a thin epoxy plate embedded with ~0.1 g (Ca_0.4Sr_0.6)Al₂Si₂O₈:1%Eu²⁺,1%Ho³⁺ (diameter 30 mm, thickness ~0.5 mm), which was irradiated with ultrasound from a transducer (Gymna Pulson 200) placed at a distance of 70 mm from the sample while the emission pattern was recorded with the CMOS camera.

3. Results

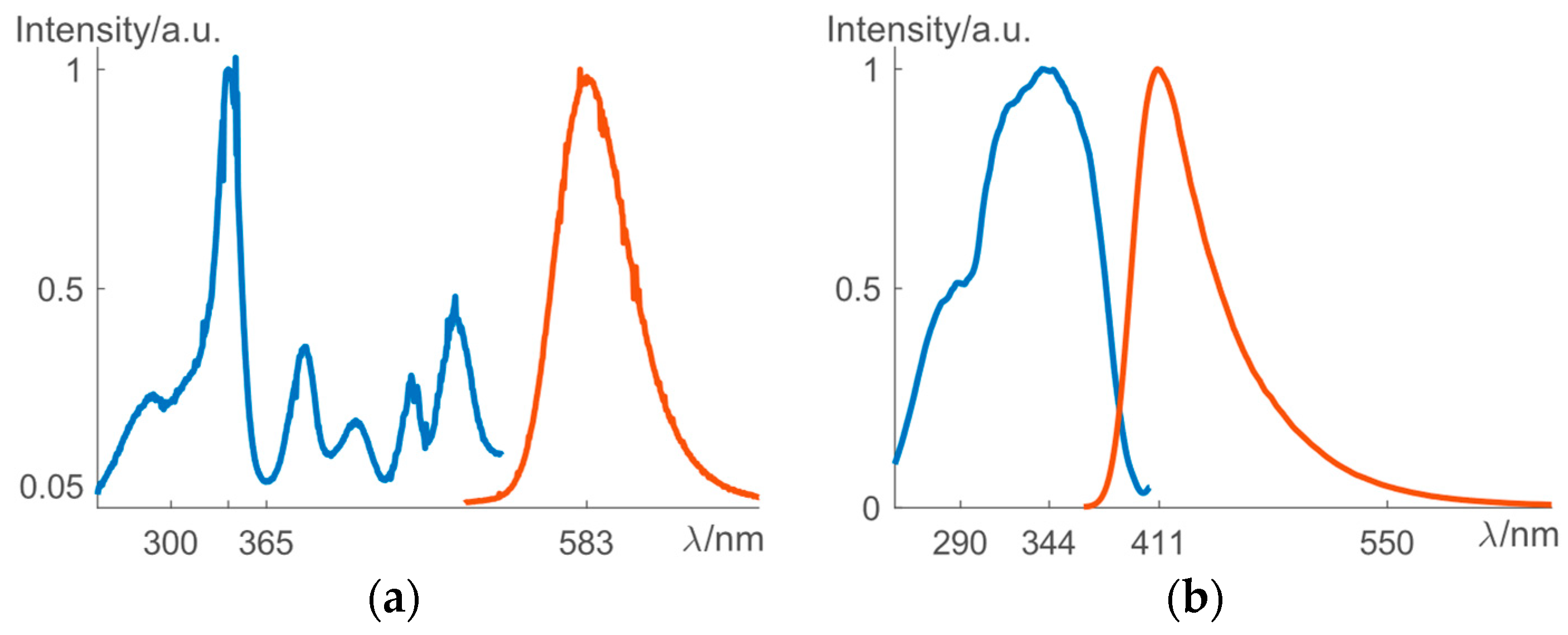
The solid-state synthesis yielded pure phases of the investigated ML materials (X-Ray diffraction patterns not shown here). As can be seen from Figure 1a, ZnS:1%Mn²⁺ can be excited efficiently by light of wavelength up to 500 nm, and its emission band is centered at 583 nm, which results in a yellow-orange color. (Ca_0.4Sr_0.6)Al₂Si₂O₈:1%Eu²⁺, 1%Ho³⁺ can be excited by UV light from 250–400 nm and the emission band is centered at 411 nm, which corresponds to a blue color (Figure 1b). Because of their non-centrosymmetric crystal structures, both phosphors show piezoelectricity, i.e., an internal electric field arises due to the application of stress. ZnS:1%Mn²⁺ is very sensitive to friction and is applicable in dynamic pressure mapping, especially above 10 MPa [7], but the response to extension was not reported yet, which could reveal interesting physics of ML.

3.1. Mechanoluminescence as a Visulization of Stress Fields

The tests on phosphor-embedded polymer discs (radius R, thickness l) display a clear ML pattern, as shown in Figure 2a, whose asymmetry is due to the imperfect loading conditions. The theoretical stress field under a diametric loading pair P (along y, −y orientations), is as follows [8]:

σ_x = −2P/(πl){(R − y)x²/[(R − y)² + x²]² + (R + y)x²/[(R + y)² + x²]² − 0.5/R},

(1)

σ_y = −2P/(πl){(R − y)³/[(R − y)² + x²]² + (R + y)³/[(R + y)² + x²]² − 0.5/R},

(2)

τ_xy = 2P/(πl){(R − y)x²/[(R − y)² + x²]² − (R + y)x²/[(R + y)² + x²]²}

(3)

and the Von Mises stress σ_VM is defined as:

σ_VM = [σ_x² + σ_y² − σ_xσ_y + 3τ_xy²]^0.5

(4)

From Figure 2b, the ML pattern agrees with the contour of σ_VM, which indicates that the deformation energy plays a vital role in inducing ML. Actually, σ_VM is directly related to the stress deviator, s_ij = σ_ij − Σσ_ii/3 through σ_VM = (1.5s_ij·s_ij)^0.5, which is responsible for the change of shape of materials [9]. On the other hand, the hydraulic stress Σσ_ii/3 is responsible for the change of volume. Thus, it is possible that mechanical loads excite various defects in ML phosphors, such as point defects, dislocations, faults, etc., and then release electrons that were stored during the excitation by UV light.

It is interesting to note that (Ca_0.4Sr_0.6)Al₂Si₂O₈:1%Eu²⁺,1%Ho³⁺ is also able to visualize the stress field produced by ultrasonic stimulation via acoustically induced piezoluminescence (APL), as shown in Figure 2c. The ring and circle at the center of the image correspond to the stress field of ultrasonic irradiation. The asymmetry is due to the imperfection of the transducer. This effect lasted tens of seconds during the ultrasonic radiation, but disappeared in 1–2 s after the ultrasound was removed.

The visualization of stress fields heavily depends on the linearity between stress and ML. This linearity can be readily confirmed in a series of tensile experiments. It is worth noting that the afterglow should be subtracted from the observed emission profile, which is the compound of net ML and afterglow, as shown in Figure 3a. For an extension from 0.00 to 0.60 mm at a rate of 1.2 mm/s, a net ML profile can be obtained, shown in Figure 3b, and the linear relationship between ML and load is clearly observed after a threshold around 2 MPa, as shown in the insect. A long tail up to tens of seconds prevails after the peak of ML, which is related to the combination of recombination with luminescent centers and re-trapping at defects of electrons liberated due to stress. The delay time between the end of the UV excitation and the application of the load influences the ML magnitude greatly. In Figure 3c, the magnitude of the ML peak drops very quickly as the delay time is increased. However, the afterglow also decays with time, resulting in the maximum ML contrast, i.e., ML/afterglow (inset of Figure 3c), after a delay of 90 s. Therefore, for visualizing stress distribution, it is important to incorporate a delay time in order to reach a good compromise between ML intensity and ML contrast.

3.2. Trap Properties as a Mean to Model Mecholuminescence

The periodic packing of atoms in crystals makes it possible to describe the energy of electrons with a certain wave vector k, i.e., E(k) in a band diagram. Here, the electrons of filled orbitals form the valence band, which is separated by the bandgap from the conduction band, where electrons can move freely in the entire crystal if they are excited above the band gap. However, doping with impurity ions such as Mn²⁺ or Eu²⁺ leads to additional energy levels inside the band gap. Special synthesis procedures (such as sintering in reducing gas, H₂) will create additional defects as well, which are able to donate/accept charge carriers to/from the crystal and even trap these charge carriers, for example in glow-in-the-dark phosphors. The concentration of traps n and the energy levels with respective to the conduction band minimum, i.e., the trap depth E_trap, play an important role. For example, electrons trapped at defects can escape at a rate p = s·exp(−E_trap/kT), contributing n∙p to the change of afterglow in many cases, in which k is the Boltzmann constant, s an attempt-to-escape frequency and T the temperature. Thermoluminescence (TL), i.e., luminescence intensity as a function of temperature while heating at a fixed rate (dT/dt = β), is a very useful tool to reveal the trap depths and trap concentration. In a TL profile, a distinct glow peak profile (at a certain temperature T_m) can correspond to a trap depth E_trap, and the area under the curve is proportional to the trap concentration. Various methods are available to calculate the trap depths, see [10] for a review.

Among these methods, the initial rise method is generally applicable to extract trap depth and does not depend on the kinetics of the detrapping mechanism of electrons [11]. It is assumed that, at the early rise of a TL peak, the rate of electrons escaping from a trap is negligible and the intensity of TL follows from

I_TL = C·exp[−E_trap/(kT)],

(5)

where k is the Boltzmann constant, T the temperature and C a constant.

For (Ca_0.4Sr_0.6)Al₂Si₂O₈:1%Eu²⁺, the introduction of 1%Ho³⁺ lowered the height of the TL peak in Figure 4a, which indicates a lower trap concentration. It also shifted the peak temperature T_m to higher values, and thus increased the trap depth from 0.623 eV (for (Ca_0.4Sr_0.6)Al₂Si₂O₈:1%Eu²⁺) to 0.638 eV as calculated from the fitting of the linear part (below 20% of the intensity at T_m) of the log(I_TL)-1/T plot in Figure 4b. Interestingly, the TL of ZnS:1%Mn²⁺ was negligible, under excitation by 302 nm (exciting ZnS host) or 365 nm (exciting mainly Mn²⁺), which meant that the trap concentration was very low, or the trap depth was so small that all traps were already emptied before the TL started [12]. It is notable that the ML of (Ca_0.4Sr_0.6)Al₂Si₂O₈:1%Eu²⁺, 1%Ho³⁺ is higher than that of (Ca_0.4Sr_0.6)Al₂Si₂O₈:1%Eu²⁺. Furthermore, ZnS:1%Mn²⁺ shows limited ML under tensile extension although its efficient ML due to friction, scratching or compression of single crystals have been reported [13]. This is probably due to the very limited trap concentration in ZnS:1%Mn, which prohibited appreciable ML. Normally, ML is due to the release of trapped electrons. However, these trapped electrons may have a different trap depth distribution from the traps responsible for afterglow. For example, deeper traps can yield ML where afterglow is minimal (a delay of 290 s still can provide ML in Figure 3c). Judging from Figure 4a–c, it is concluded that the traps in (Ca_0.4Sr_0.6)Al₂Si₂O₈:1%Eu²⁺ responsible for ML are situated in the deeper part of the trap depth distribution. Therefore, the introduction of Ho³⁺ enhances ML as it shifts the traps to larger depth although the trap concentration is only slightly decreased. The ML contrast was hereby improved from 0.15 (for (Ca_0.4Sr_0.6)Al₂Si₂O₈:1%Eu²⁺) to 0.28 (for (Ca_0.4Sr_0.6)Al₂Si₂O₈:1%Eu²⁺,1%Ho³⁺). The combination of a reduction of trap concentration and an increase of trap depth is responsible for the improvement.

This indicates that tuning the trap depths and trap concentration is a useful way to tailor the properties of ML according to specific applications such as stress visualization, APL, or ML displays. This is possible when the traps responsible for ML are already known for the studied materials.

4. Conclusions

Mechanoluminescent phosphors offer an alternative technique for stress visualization based on the linearity between stress and mechanoluminescence. The anorthite (Ca_0.4Sr_0.6)Al₂Si₂O₈:1%Eu²⁺,1%Ho³⁺ is applicable for stress visualization and APL visualization. The inclusion of Ho³⁺ shifts the trap depth to larger values and slightly lowers the trap concentration, thus increasing the ML intensity and the contrast of ML to afterglow. Tailoring trap properties is vital for tuning ML phosphors for various applications.