Experimental Measurement of Pressure Loading from Near-Field Blast Events: Techniques, Findings and Future Challenges ^†

Abstract

The accurate characterisation of pressure loads imposed on structural members following the detonation of a high explosive is critical to our ability to design protective systems. This poses serious challenges for experimentalists, due to the high magnitude and short duration of loading. If the distance from the detonation to the target is relatively large, the loading is imparted through the interaction of a shock wave travelling away from the detonation through the surrounding medium, say air. Here, pressure magnitudes are typically in the range 10³–10⁶ Pa and are measurable using conventional, commercially available piezo-electric or piezo-resistive pressure transducers. A considerable effort has been expended on experimentally characterizing these “far-field” loads and consequently, we have a strong understanding of the mechanisms and magnitudes of loading. However, we are also interested in the loading when the target is very close to the detonation, for a range of protection applications, from aviation security to the design of personnel protection. Here, very different physical processes dominate. At these so-called “near-field” distances from a detonation (<~1 m/kg_TNT^1/3) the high temperature gaseous detonation products are still violently expanding, and loading on a target is generated by the impingement of both the shocked surrounding material and these products themselves. Blast pressures are often higher that the yield strength of structural materials and temperatures can reach several thousand Kelvin. Furthermore, loading can vary by an order of magnitude over very short distances and timescales. This paper will describe experimental work conducted at University of Sheffield on developing approaches to accurately measure and predict near-field blast loading and gain a better understanding of the underlying mechanisms of loading. The challenges inherent to this field of work will be discussed and an attempt made to identify some of the emerging themes for future research.

1. Introduction

The ability of engineers to safely and efficiently design any structural system is dependent on the accurate prediction of the loading which the structure may be expected to encounter. When designing structures to withstand a high explosive blast, we therefore need to be able to predict the form and magnitude of the loading imparted to a structural system by the effects of the detonation. Loading may include thermal effects and impacts from casings around the explosive or from objects adjacent to the explosion which are turned into projectiles by the blast, but this article will concentrate on the mechanical pressure loading developed by the explosion when surrounded by air.

A high explosive detonation in air involves the near-instantaneous decomposition of solid or liquid compounds, generally formed of molecules of carbon, hydrogen, nitrogen and oxygen into predominantly gaseous form. The resulting “fireball”, initially at extremely high temperature (typically several thousand K) and pressure (>10 GPa) expands with initial velocity of several thousand m/s, displacing and highly compressing the adjacent air. In the early stages of expansion, the displaced air is compressed into a thin shell between the fireball and a shock front which separates the compressed air from the still-undisturbed air ahead of it. As expansion continues, the pressure and expansion velocity of the fireball rapidly decay, and, for a spherical explosive charge, the fireball stops expanding at a radius of around 20 times that of the undetonated charge, or a scaled distance of around 1 m/kg^1/3. The shock wave generated in the surrounding air continues to propagate outwards until it interacts with some obstacle or target.

2. Far-Field Blast

When the fireball expansion has ceased and the air shock has fully detached, the mechanisms of the air shock propagation and the pressures associated with it are relatively straightforward to predict, given the initial conditions. Friedlander [1] showed that the form of the far-field blast wave is a sharp rise to peak pressure followed by an exponential decay. The pressure above ambient conditions, (“overpressure” p) associated with the blast wave at any time t after detonation can be expressed by the modified Friedlander equation as:

$$p\left(t\right)=p_{max}\left(1-t/t_d\right)e^{-bt/t_d}$$

(1)

where p_max is the maximum overpressure, t_d is the duration of the positive phase of the blast wave and b is a waveform parameter which describes the shape of the exponential decay.

Predictions of the magnitudes of the parameters of the modified Friedlander equation, determined from an analysis of the shock relations and experimental data from instrumented blast trials, were presented by Kingery & Bulmash (K&B) [2]. The K&B predictions apply for the parameters associated with the unhindered propagation of the blast wave (“side-on” or “incident” conditions) and also where the blast wave is normally reflected by a rigid target (“reflected” conditions). Several studies of well controlled small-scale experimental blast testing have shown the K&B predictions for normally reflected conditions to be remarkably accurate at scaled distances greater than about 2 m/kg^1/3 (e.g., [3,4,5]).

The K&B analysis does provide predictions for the blast wave parameters in the near-field, but these have generally been considered to be of questionable provenance, since they are based on analysis of a freely-propagating air shock, whereas in the near-field, the air shock is still being driven by the expanding fireball. The situation is still more complex for reflected blast waves in the near-field, since the air shock does not simply reflect back into air, but will interact with the still-expanding fireball. Numerical modelling of near-field blast suggests that the waveform [6,7] and magnitudes of some parameters, in particular the peak overpressure [8] may vary from the K&B predictions. However, there has been relatively little definitive experimental work conducted into this issue.

3. Near-Field Blast

The far-field experimental work described in the previous section typically involved peak over pressures in the sub-MPa range. These pressures are easily measurable using piezo-electric or piezo-resistive pressure gauges, which are commercially available at relatively low-cost with >100 kHz bandwidth to enable short duration transients to be identified. Experimental measurement of near-field blast parameters is considerably more taxing, as the predicted peak overpressures increase rapidly with reducing scaled distance. This together with the very high temperatures associated with the fireball renders conventional pressure transducers unsuitable.

An often-used alternative approach is to measure the momentum imparted to freely-flying metal plates or plugs loaded by the impingement of the blast wave (e.g., [9]). If the momentum traps are sufficiently small in frontal area, this can provide useful information on the specific impulse (impulse per unit area) imparted to a target, but it gives little insight into the wave form or the magnitude of peak overpressure.

In fact, a suitable method for measuring extremely high dynamic pressures was developed more than 100 years ago by Bertram Hopkinson [10] with the development of what became known as the “Hopkinson pressure bar” (HPB). This is now far more widely known in the split-HPB form, used for determination of the high strain-rate mechanical properties of materials, but in its original form, the HPB was essentially a robust high pressure transducer. Hopkinson’s equipment comprised a single long, cylindrical bar, loaded at one end, with a momentum trap at the distal end. By repeating nominally identical tests and measuring the impulse imparted to different lengths of momentum trap, Hopkinson was able to extract rudimentary time histories of loading from intense dynamic events.

Despite the development of the HPB in the mid C20th to include direct measurements of strain pulses propagating along the bar, it has been used relatively sparingly as a pressure transducer. Edwards et al. [6] and Esparza [11] conducted a series of tests on detonations in air, using HPBs as near-field pressure transducers, whilst Lee et al. [12] conducted similar work measuring loading from underwater explosions and Fourney and co-workers at University of Maryland have used instrumented HPBs to measure the loading from the detonation of shallow-buried charges [13].

4. University of Sheffield “COBL” Facility

Motivated by the studies noted in the previous section, and their own extensive studies of the HPB as an impact pressure transducer [14], the Blast & Impact Group at University of Sheffield (UoS) developed an experimental facility for measuring near-field blast pressures. The Characterisation of Blast Loading (COBL) facility was originally designed in collaboration with the UK Defence Science and Technology Laboratory to measure loading from shallow-buried explosive charges [15] and was later used to measure reflected pressures from spherical charge explosions in air [16].

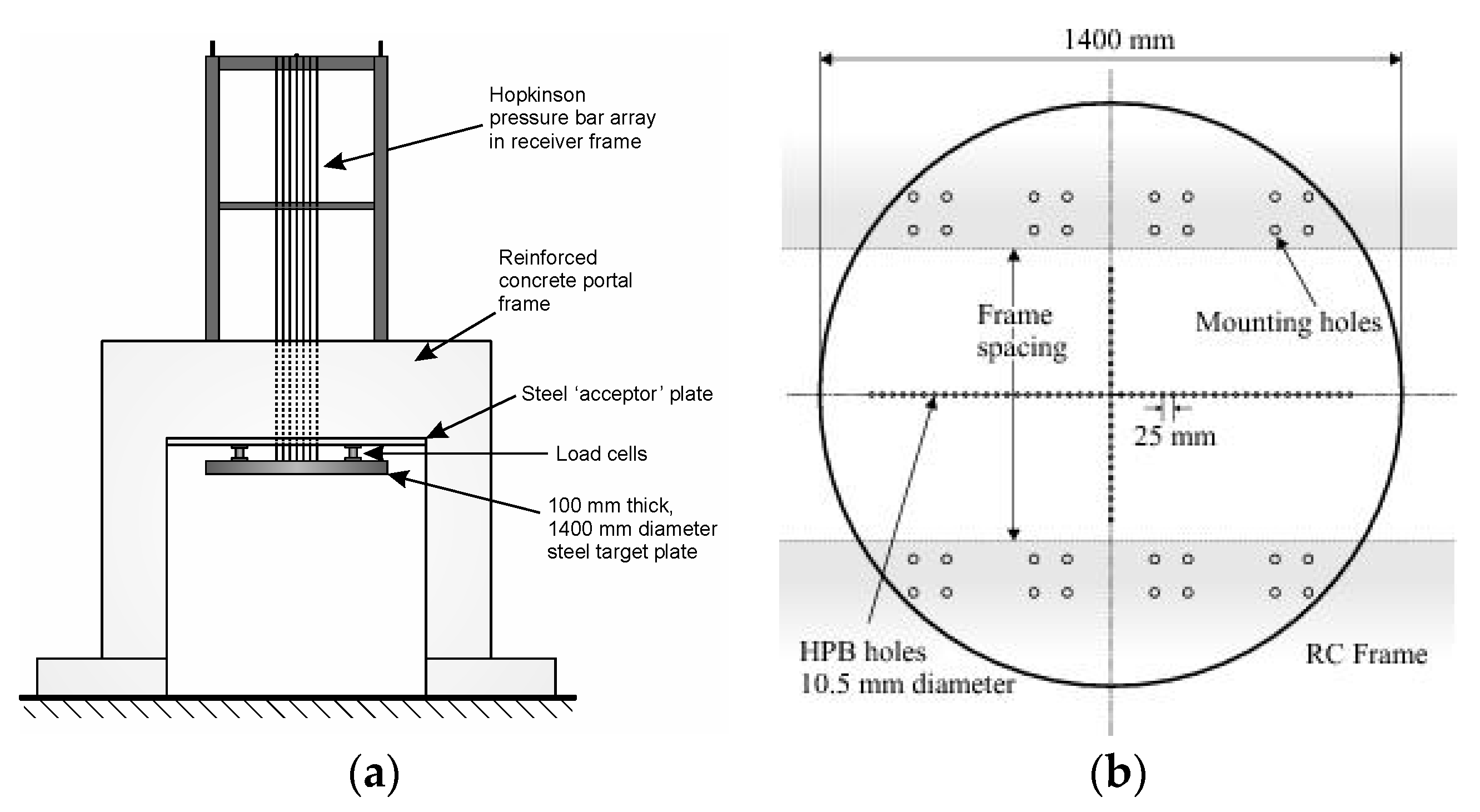
The COBL facility comprises a series of 10 mm diameter EN24T HPBs, placed through close tolerance holes set in a 100 mm thick steel reflecting target plate such that the loading end of the HPBs are flush with the underside of the plate (Figure 1). The target plate is underslung from the soffits of two parallel reinforced concrete portal frames which are approximately 2 m high to the soffit and 2 m clear span, with cross beams 750 mm deep by 500 mm wide; the entire facility is therefore a stiff, massive reaction frame with a grid of discrete measurement points distributed along the target face. Typically, 17 HPBs are used in a test, with one set at the central hole and 4 each at radii of 25, 50, 75 and 100 mm. The explosive charge is suspended below the target plate on a light woven glass-fibre fabric (~25 g/m² areal density) to provide as little obstruction as possible whilst allowing accurate placement. Charge masses of 50–250 grammes TNTeq have been detonated, at a range of clear distances from 70–400 mm. In total, more than 100 tests in air have been conducted.

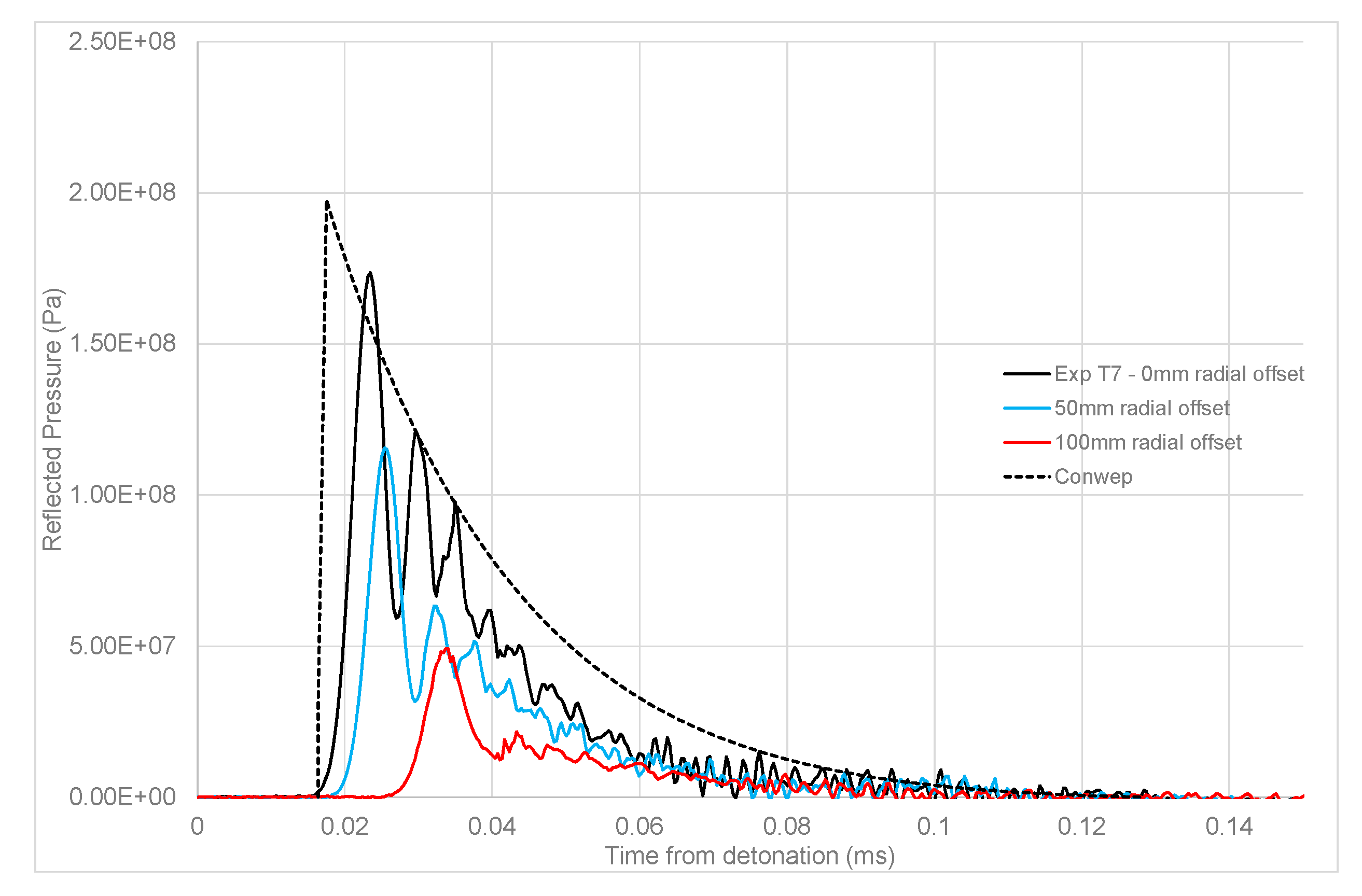
A typical set of overpressure-time test results is shown in Figure 2, from the detonation of a 113 gramme sphere of PE10 explosive (86% PETN, 14% mineral oil binder/plasticiser) set at 70 mm clear stand-off from the target plate. Results from the central bar (normal reflection) and the averages of the four bars at both 50 mm and 100 mm radial offset are shown. Also shown on Figure 2 is the predicted normally reflected load from the ConWep computer code [17] which is based on the K&B approach. Figure 3 shows a summary of UoS experimental data for normally reflected blast parameters (peak pressure, specific impulse, and times of arrival duration of the load) from both COBL tests (scaled distance < 1 m/kg^1/3) and arena trials with conventional piezo-resistive pressure gauges (scaled distance > 1 m/kg^1/3) for both PE10 and PE4 explosives. In general, the K&B predictions are remarkably accurate, even down to very close proximity to the charge. However two issues do stand out. Firstly, as the scaled distance reduces, the K&B method generally over-predicts the magnitude of the specific impulse. This over prediction can clearly be seen in Figure 2. This is believed to be simply because the K&B analysis, based on assumptions of far-field loading, implicitly assumes that the blast wave is effectively parallel with a target surface. At in the very near field however, there is a high curvature to the blast front as it strikes a flat target; this means that the load across the target face is highly non-uniform, resulting in rarefaction waves expanding out from the centre, reducing the epicentral pressure and leading to a state of uniform pressure across the instrumented region by around 0.07 ms after detonation in Figure 2. Consequently, the K&B prediction for specific impulse near the centre of the loaded region are generally somewhat high.

Secondly, the data in Figure 3 clearly show a relatively high variability around a scaled distance of 1 m/kg^1/3. This is due to the development of Rayleigh-Taylor and Richtmyer-Meshkov instabilities at the interface between the fireball and the shocked air around it. This is a well-known concept, but we have found no previous studies of the effect of these features on pressure loading. In the UoS COBL tests, digital high speed video (DHSV) has been used to capture the expansion of the fireball at framing rates of up to 500,000 fps, which allows us to see the development of these instabilities and synchronise them to features on the loading pulses. DSHV evidence of these instabilities is shown in Figure 4. Interestingly, this does not appear to be a scale-dependent issue, with near-identical features also visible on stills of the fireball from the 4.7 kiloTonne ANFO Minor Scale detonation. 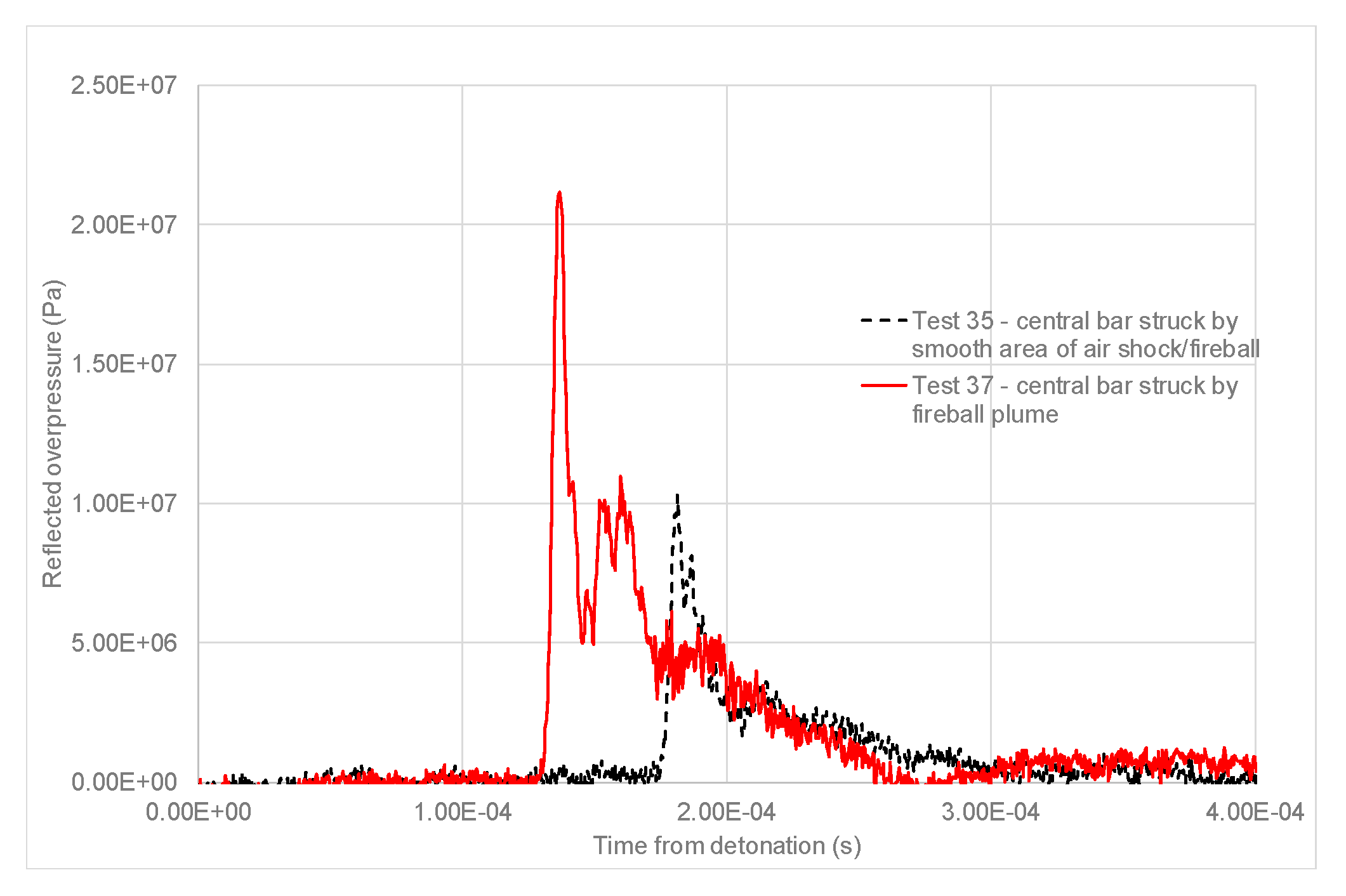Figure 5 shows the effect of these instabilities on the loading measured by the central bar in the COBL facility in two nominally identical tests at a scaled distance to the target plate of 0.76 m/kg^1/3, with arrival time, peak pressure, duration and specific impulse all significantly affected when one of the instability structures of the fireball strikes the bar. Variations on this scale appear to be confined to the time and distance at which the fireball expansion begins to terminate; such variations are not seen at significantly lower and higher scaled distances. The UoS team believes that at lower scaled distances, the instabilities have not had time to form, whereas at significantly greater distances, variations in the structure and intensity of the detached air shock will have had time to equalise through energy flow from the higher-to-lower pressure regions. This clearly has implications for the consistency which may be expected from experimental blast testing of materials and structures at scaled distances around 0.5–2 m/kg^1/3.

5. Conclusions and Future Challenges

Results such as those shown in the previous section are useful both for establishing the validity of quick prediction methods such as the K&B approach, and for validation of numerical modelling studies. Most importantly, they show that we have the potential to better understand the mechanisms and features of blast loading on targets very close to a detonation. This is of key interest for experimental and numerical modelling studies of the response of materials and structures to near-field loading, and points the way to establishing such work on a firmer scientific footing. In particular, COBL offers us a means to study the effect of approaches to mitigate the loading generated in near-field blast events.

However, we are far from a full understanding of blast in the near-field. Only geometrically simple arrangements have been explored to date (spherical charges, flat target plates) and the question of loading with different shapes of charge and target is still open to investigation. Initial testing has been conducted on the COBL facility suggest that “afterburn”, a rapid, exothermic chemical reaction of the partially-oxidised detonation products mixed with oxygen from the surrounding air, has a significant influence on the near-field reflected pressures. This feature is not considered in most numerical modelling approaches to detonation and blast loading and further experimental work is required for confirmation and quantification before firm recommendations can be given. Such studies will require us to integrate high-speed pyrometry into the COBL facility to gain a more complete understanding of the thermodynamics of these events.