Damage Identification Using Sub-Microstrain FBG Data from a Pre-Stressed Concrete Beam During Progressive Damage Testing †
Abstract
:1. Introduction
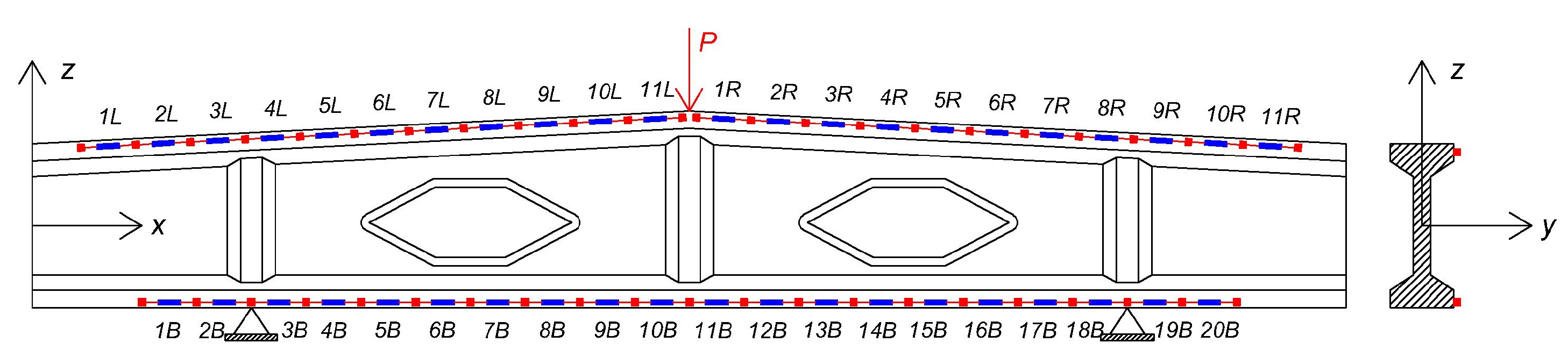
2. Experimental Setup
2.1. Dynamic Tests
2.2. Progressive Damage Test
3. Modal Analysis
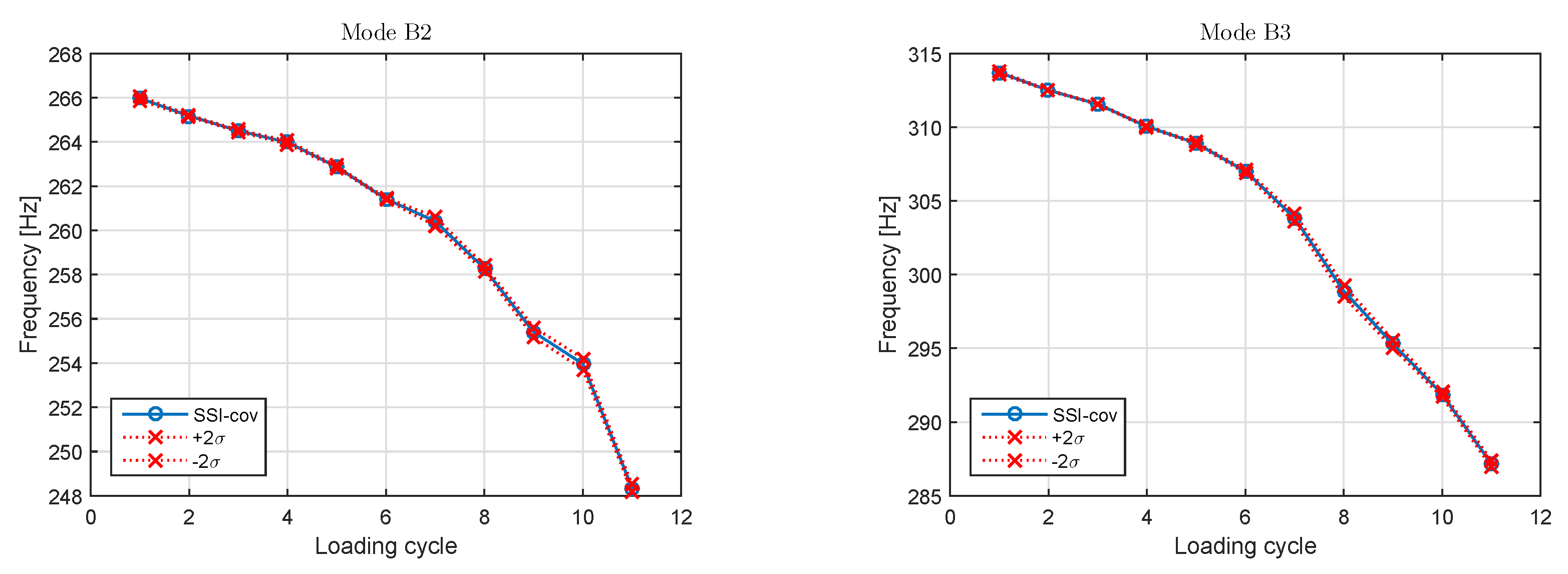
3.1. Eigenfrequencies
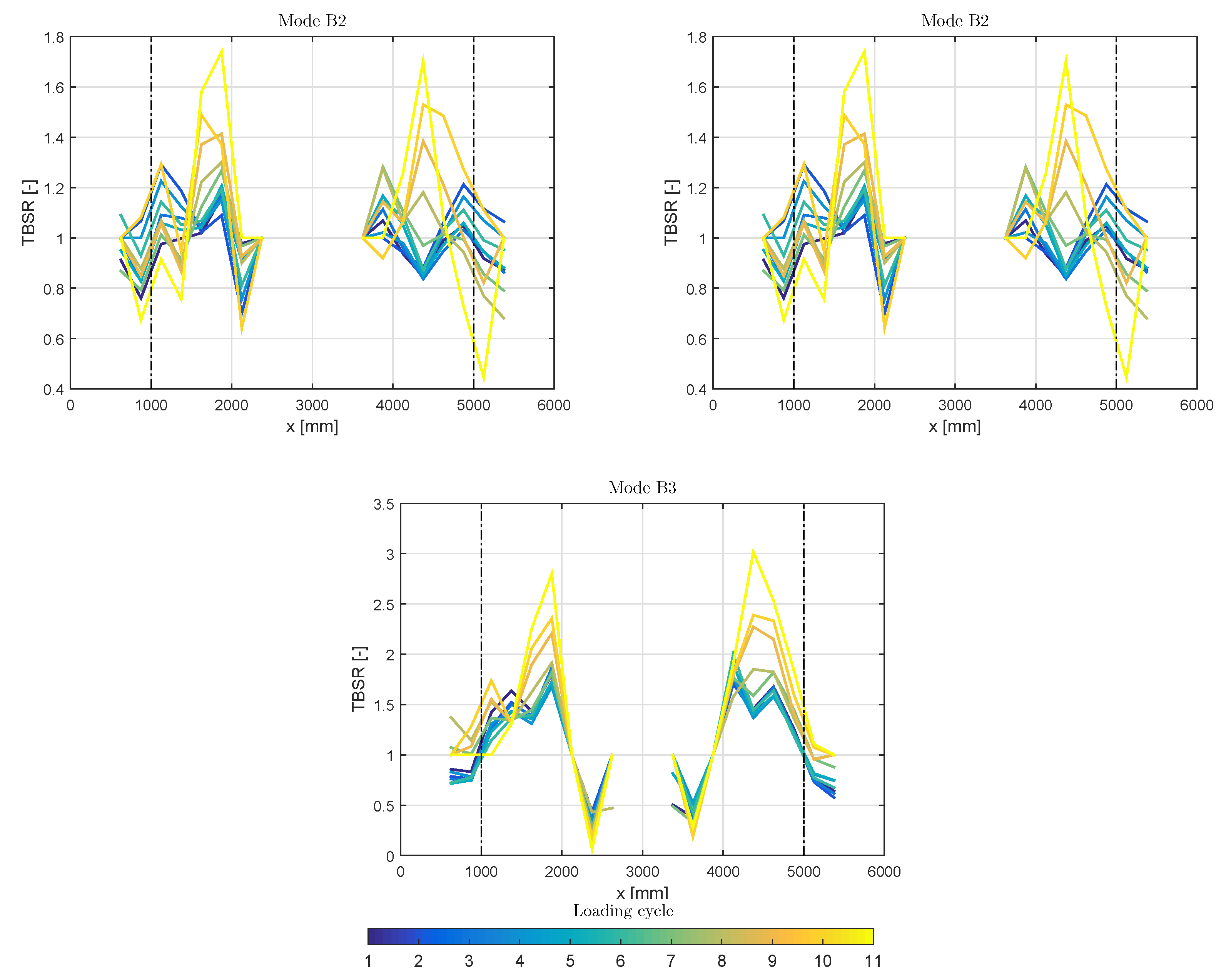
3.2. Strain Mode Shapes
4. Conclusions
Acknowledgments
References
- Deraemaeker, A.; Reynders, E.; de Roeck, G.; Kullaa, J. Vibration based Structural Health Monitoring using output-only measurements under changing environment. Mech. Syst. Signal Process. 2008, 22, 34–56. [Google Scholar] [CrossRef]
- Peeters, B.; de Roeck, G. One-year monitoring of the Z24-bridge: Environmental effects versus damage events. Earthq. Eng. Struct. Dyn. 2001, 30, 149–171. [Google Scholar] [CrossRef]
- Unger, J.F.; Teughels, A.; de Roeck, G. Damage detection of a prestressed concrete beam using modal strains. Struct. Eng. 2005, 131, 1456–1463. [Google Scholar] [CrossRef]
- Glisic, B.; Inaudi, D. Fibre Optic Methods for Structural Health Monitoring; John Willey & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Meltz, G.; Morey, W.W.; Glenn, W.H. Formation of Bragg gratings in optical fibers by a transverse holographic method. Opt. Lett. 1989, 14, 823–825. [Google Scholar] [CrossRef] [PubMed]
- Anastasopoulos, D.; de Smedt, M.; Vandewalle, L.; de Roeck, G.; Reynders, E. Damage identification using modal strains identified from operational fiber-optic bragg grating data. Struct. Health Monit. 2018. [Google Scholar] [CrossRef]
- Reynders, E.; Schevenels, M.; de Roeck, G. MACEC 3.3: A Matlab Toolbox for Experimental and Operational Modal Analysis; Report BWM-2014-06; Leuven University: Leuven, Belgium, 2014. [Google Scholar]
- Reynders, E.; Maes, K.; Lombaert, G.; de Roeck, G. Uncertainty quantification in operational modal analysis with stochastic subspace identification: Validation and applications. Mech. Syst. Signal Process. 2016, 66–67, 13–30. [Google Scholar] [CrossRef]


| Method | Mode L1 | Mode T1 | Mode L2 | Mode T2 | Mode B1 | Mode L3 |
|---|---|---|---|---|---|---|
| EMA | 27.20 | 35.50 | 75.30 | 93.00 | 127.50 | 131.00 |
| FEM | 27.40 | 55.40 | 77.15 | 108.70 | 115.40 | 141.90 |
| Method | Mode T3 | Mode L4 | Mode T4 | ModeB2 | Mode B3 | |
| EMA | 178.00 | 216.60 | 244.80 | 265.90 | 313.70 | |
| FEM | 177.80 | 234.50 | 247.70 | 264.40 | 314.40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anastasopoulos, D.; Smedt, M.D.; Roeck, G.D.; Vandewalle, L.; Reynders, E.P.B. Damage Identification Using Sub-Microstrain FBG Data from a Pre-Stressed Concrete Beam During Progressive Damage Testing. Proceedings 2018, 2, 462. https://doi.org/10.3390/ICEM18-05367
Anastasopoulos D, Smedt MD, Roeck GD, Vandewalle L, Reynders EPB. Damage Identification Using Sub-Microstrain FBG Data from a Pre-Stressed Concrete Beam During Progressive Damage Testing. Proceedings. 2018; 2(8):462. https://doi.org/10.3390/ICEM18-05367
Chicago/Turabian StyleAnastasopoulos, Dimitrios, Maure De Smedt, Guido De Roeck, Lucie Vandewalle, and Edwin P. B. Reynders. 2018. "Damage Identification Using Sub-Microstrain FBG Data from a Pre-Stressed Concrete Beam During Progressive Damage Testing" Proceedings 2, no. 8: 462. https://doi.org/10.3390/ICEM18-05367
APA StyleAnastasopoulos, D., Smedt, M. D., Roeck, G. D., Vandewalle, L., & Reynders, E. P. B. (2018). Damage Identification Using Sub-Microstrain FBG Data from a Pre-Stressed Concrete Beam During Progressive Damage Testing. Proceedings, 2(8), 462. https://doi.org/10.3390/ICEM18-05367





