Abstract
Creep life prediction is very important to maintain safe operation of thermal power plants for a long-term period. In this study, an alternative creep life prediction method was proposed based on a relationship between creep exponent n and creep coefficient k. A high temperature indentation creep test was conducted to identify the creep exponent and creep coefficient for each specimen with different creep damage ratio. Subsequently, the relationship between the creep coefficient and creep exponent for each creep damage ratio was focused on. As a result, it was confirmed that a new parameter introduced based on both creep coefficient and creep exponent linearly increase as the creep damage ratio increases. Furthermore, the is uniquely determined by the creep damage ratio regardless of the temperature and stress conditions. These results indicate that the creep life can be predicted with a high accuracy using the .
1. Introduction
Typical accidents in thermal power plants occur primarily due to creep damage. Thus, predicting the creep life is very important to maintain safe operation of thermal power plants for a long-term period. A destructive testing technique can predict accurately the creep life compared to other techniques. However, the associated technique has some problems: the specimen must be extracted from an actual plant, etc.
We conducted a high-temperature indentation test to estimate a creep constitutive equation, known as Norton’s law [1,2]. The high-temperature indentation test can be placed as intermediate one between destructive and nondestructive tests. The Norton’s law relates between the creep strain rate and stress σ as follows.
where k and n denote the creep coefficient and creep exponent, respectively. The creep coefficient and creep exponent can be accurately identified from the relationship between the time and the impression size.
Walser et al. conducted uniaxial creep tests for unused and wasted boiler tubes and investigated the relationship between the creep exponent and operating time [3]. As shown in Figure 1, the result showed that the creep exponent increases monotonically with the increase in the operating time. Consequently, they stated that the creep exponent has capability to predict the creep life. It is, however, difficult to apply their method to an actual component because several large specimens must be cut off from the component. In contrast, the creep exponent and creep coefficient can be determined via the high-temperature indentation creep test only once. Therefore, the high-temperature indentation creep test is expected to be a practical technique for the creep life prediction.
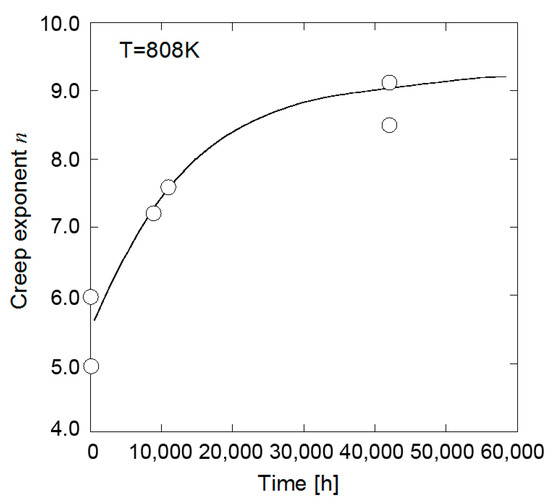
Figure 1.
Relationship between creep exponent and operating time [3].
In this study, a uniaxial creep test was conducted to prepare specimens with different creep damage ratios. Subsequently, the high-temperature indentation creep test was conducted to determine the creep exponent and creep coefficient for each specimen. From those results, we proposed a creep life prediction method based on the relationship between the creep exponent and creep coefficient.
2. Estimation of Creep Constitutive Equation by High-Temperature Indentation Creep Test
2.1. High-Temperature Indentation Creep Test
In the high-temperature indentation creep test, the relationship between the impression size and the testing time is obtained by indenting a specimen with a spherical ball under a high-temperature environment. The creep exponent and creep coefficient in the Norton’s law can be estimated from the relationship. The estimation method is as follows.
When semi-infinite creep media were indented with a spherical ball, the relationship between the spreading ratio of the impression radius and indentation load can be given as follows.
where represents the non-dimensional impression radius ratio,
and
R and P denote the radius of indentation ball and indentation load, respectively. Then, η is the correction coefficient given as follows.
where r is the radius of the specimen. The procedure to evaluate the creep constitutive equation is shown in Figure 2. In performing the high-temperature indentation creep test, the impression radius a needs to be measured at several intervals of time t under a constant loading condition P, wherein a logarithm of the non-dimensional impression ratio is plotted as a function of the logarithm of the mean contact pressure . The creep exponent and coefficient can be identified from the gradient and vertical axis intercept on the graph.
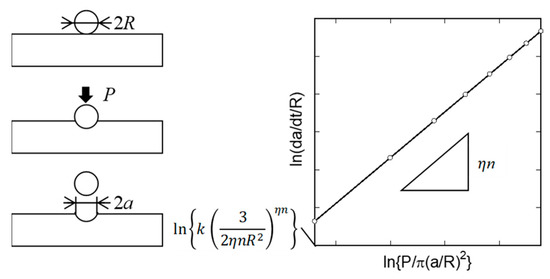
Figure 2.
Procedure to estimate creep constitutive equation by high-temperature indentation creep test.
2.2. Specimen Preparation and Test Procedure
In order to prepare the specimens with different creep damage ratio for the high-temperature indentation creep test, a uniaxial creep test was conducted. ASME Grade 122 steel, which is candidate material of advanced-ultra super critical thermal power plants, was employed for the uniaxial creep test. The shape of the specimen is a parallel part size of φ 4 × 5 mm which is nonstandard shape. An original uniaxial-creep testing system based on the lever rule with a leverage ratio of 1:10 was used for the small specimen. The uniaxial creep test was performed under two testing conditions; one is 923 K and 120.4 MPa, the other is 973 K and 70.8 MPa. The displacement of the specimen was measured using a dial gauge set at the lever. Under these testing conditions, a creep rupture test was conducted to identify the rupture time. Subsequently, three specimens with different creep damage ratios Φ = 0.25, 0.50, and 0.75 were prepared based on this rupture time.
Figure 3 shows the experimental procedure to conduct the high-temperature indentation test for the interrupted specimen. The cylindrical specimen was cut off at the parallel part of the specimen as shown in Figure 3. The cut surface was polished using a buff with a diamond suspension. The high-temperature indentation test was conducted for the polished surface using an original high-temperature indentation testing machine with a leverage ratio of 1:3, as shown in Figure 3. An alumina ball with a diameter of 4 mm was employed as the indenter. The testing temperatures corresponded to those in the uniaxial creep test. The indentation load was fixed at 331.4 N. The indentation test was interrupted every 100 h to record variation of the impression radius with time. The impression radius a was measured using a digital microscope (TMR-1, YASHIMA OPTICAL CO., LTD., Tokyo). The indentation test was performed for approximately 500 h.
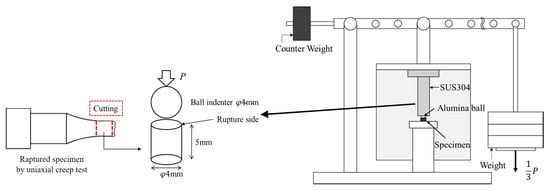
Figure 3.
Schematic illustration of high-temperature indentation creep testing system and specimen.
2.3. Creep Exponent and Creep Coefficient
Figure 4 shows the creep exponent and creep coefficient evaluated by the high-temperature creep indentation test as a function of creep damage ratio. In Figure 4a, the creep exponent linearly increases as the creep damage ratio increases in each specimen. Further, the specimen damaged under the condition of 923 K and 120.4 MPa has larger creep exponent than the specimen damaged under the condition of 973 K and 70.8 MPa. In contrast, the creep coefficient slightly decreases as the creep damage ratio increases. In addition, the specimen damaged under the condition of 923 K and 120.4 MPa has smaller creep coefficient than the specimen damaged under the condition of 973 K and 70.8 MPa. These results imply that the creep life can be predicted by using the creep exponent and creep coefficient.
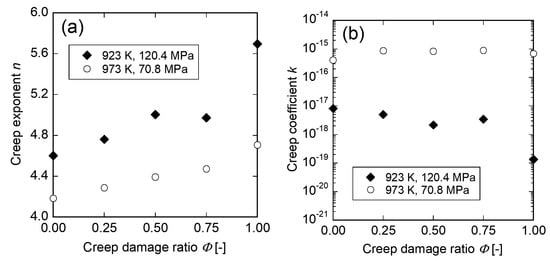
Figure 4.
Dependency of creep exponent and creep coefficient estimated by the high-temperature creep indentation test on creep damage ratio; (a) creep exponent, (b) creep coefficient.
3. Proposal of New Creep Life Prediction Method Based on Creep Exponent and Creep Coefficient
3.1. Conventional Method Based on Vickers Hardness
As an instance of conventional creep life prediction methods, Vickers hardness method was applied to the specimens prepared in Section 2.2. The relationship between the hardness difference and creep damage ratio is shown in Figure 5. The Vickers hardness difference represents the difference between the Vickers hardnesses of the grip part (HV0) and testing area (HV) in the interrupted specimen. The Vickers hardness difference monotonically increases as the creep damage ratio increases. However, the Vickers hardness difference varies strongly depending on the temperature and stress levels which the specimens have experienced, even though the specimens have same creep damage ratio each other. Therefore, in order to apply the Vickers hardness method to actual components, we have to preliminarily obtain the relationship between the hardness difference and creep damage ratio in various temperature and stress conditions.
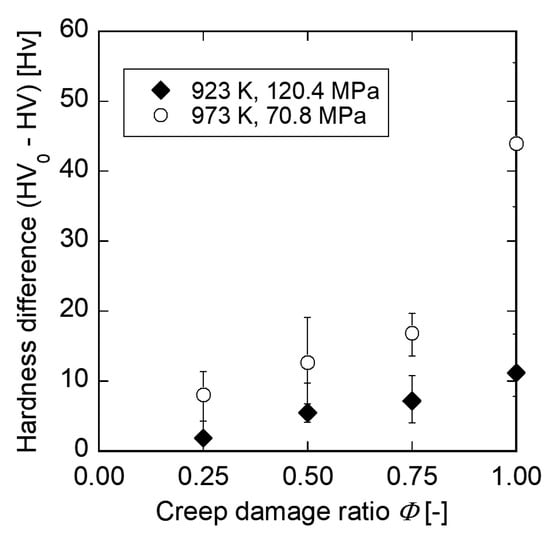
Figure 5.
Relationship between hardness difference and creep damage ratio.
3.2. Proposal of New Parameter for Creep Life Prediction
As shown in Figure 4a, the creep exponent and creep coefficient also varied depending on the temperature and stress levels which the specimen has experienced. In order to develop a more practical creep life prediction method based on the creep exponent and creep coefficient, we proposed a new parameter which is uniquely determined by the creep damage ratio regardless of the temperature and stress conditions.
F.K.G. Odqvist and J. Hult have reported that a logarithm of the creep coefficient can be linearly plotted as a function of the creep exponent in typical heat resistant steels [4]. The relationship between the creep exponent and a logarithm of the creep coefficient in other materials including non-ferrous metals and ceramics has been investigated by T. Mita et al. [5]. As the result, the linear relationship was also observed in the materials, in addition, the gradient and vertical axis intercept on the graph depended on the material. According to these researches, the relationship between the creep exponent and creep coefficient can be expressed as,
where A and B are constants depending on material. We focused on the relationship expressed as Equation (6) to develop a new parameter for creep life prediction.
The relationship between the creep exponent and a logarithm of creep coefficient obtained through the high-temperature indentation creep test is plotted in Figure 6. In the graph, the approximate lines are drawn for each creep damage ratio. It is confirmed that the gradient A of approximate lines is almost constant with creep damage ratio, in contrast, the intercepts B of approximate lines are changed with creep damage ratio. Equation (6) is rewritten as,
If the A is constant, the logarithm of B can be determined by the creep exponent and creep coefficient obtained through the high-temperature indentation creep test. The gradient of approximate line for the unused specimen (Φ = 0.0) shown in Figure 6 was employed as the constant A.
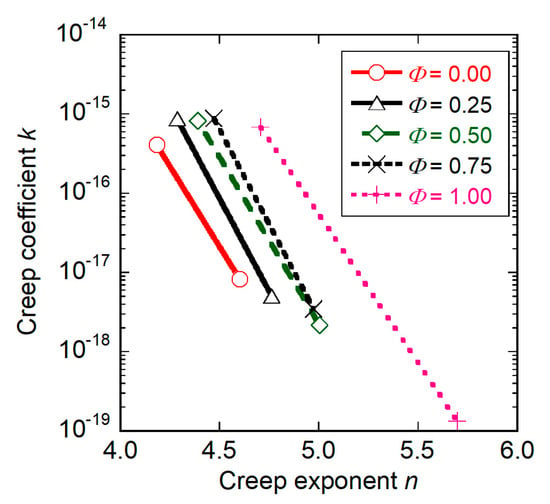
Figure 6.
Relationship between creep exponent and creep coefficient.
The logarithm of B normalized by the logarithm of B0, which is denoted by , is plotted as a function of the creep damage ratio in Figure 7. The logarithm of B0 is obtained from the unused specimen using Equation (7). In Figure 7, the linearly increases as the creep damage ratio increases. Furthermore, the is not affected by the temperature and stress conditions. The approximate line is expressed as,
where and for our material. The correlation coefficient ρ was evaluated to be 0.959. Equation (8) indicates that the is uniquely determined by the creep damage ratio. Consequently, the creep life of material can be predicted with a high accuracy using the parameter.
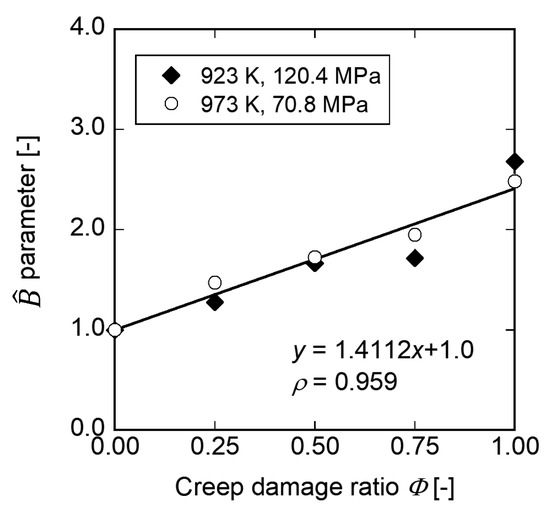
Figure 7.
Relationship between parameter and creep damage ratio.
4. Conclusions
In this study, the creep exponent n and creep coefficient k on specimens with different creep damage ratios were evaluated via the high temperature indentation creep test. As the result, a creep life prediction method was proposed based on the new parameter , which is uniquely determined by the creep damage ratio regardless of the temperature and stress conditions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Arai, M.; Takahashi, Y.; Kumagai, T. Determination of high-temperature elastoplastic properties of welded joints by indentation test. Mater. High Temp. 2015, 32, 475–482. [Google Scholar] [CrossRef]
- Arai, M. High-Temperature Creep Property of High-Cr Ferritic Heat-Resisting Steel Identified by Indentation Test. J. Press. Vessel Technol. 2016, 139, 021403. Available online: http://pressurevesseltech.asmedigitalcollection.asme.org/article.aspx?articleID=2530154 (accessed on 27 September 2016). [CrossRef]
- Walser, B.; Rosselet, A. Determining the Remaining Life of Superheated Steam Tubes by Creep Tests and Structural Examinations. Sulzer Tech. Rev. 1978, 1978, 37–44. [Google Scholar]
- Odqvist, F.K.G.; Hult, J. Kriechfestigkeit Metallischer Werkstoffe; Baihukan: Tokyo, Japan, 1967; pp. 286–287. (In Japanese) [Google Scholar]
- Mita, T.; Misumi, M.; Ohkubo, M. Characteristics of Stress Index in Norton’s law. In Proceedings of the 54rd NCTAM National Congress of Theoretical and Applied Mechanics, Tokyo, Japan, 25–27 January 2005. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).