Classifying UAVSAR Polarimetric Synthetic Aperture Radar (PolSAR) Imagery Using Target Decomposition Features ^†

Abstract

Changes in the earth’s surface significantly increase natural disasters, resulting in severe damage to man-made objects, such as roads, buildings, bridges, and so on. Radar techniques have advantages, such as lack of sensitivity to weather conditions, to night and day, and to cloud cover conditions, which can be used to identify, alert, and mitigate these damages. Because of the importance of these areas and the need to care for them, land-use classification, one of the important applications of remote sensing, is performed. Polarimetric synthetic aperture radar (PolSAR) images have many capabilities, having the scattering information on four polarized levels (HH, HV, VH and VV) and consequently depending on the shape and structure of the environment. In this study, unmaned aerial vehicle (UAVSAR) image is used. The support vector machine (SVM) model is a well-known classification method, able to run on different types of features and to distinguish classes that are not linearly separable. On the other hand, it is possible to use data mining methods to facilitate data analysis, like classifications. In this regards, it is recommended to use the random forest (RF) technique. The RF is one of the useful methods for data classification which uses a tree structure for decision-making. This method uses strategies to enhance the probability of reaching goals with conditional probability. In this study, by incorporating a variety of target decomposition methods in PolSAR images, images producing the land cover types were generated. Then, 70 features were obtained by applying the support vector machine (SVM), random forest (RF), and K-nearest neighbor (KNN) classification methods. In order to estimate accuracy, the output of these methods was evaluated by reference data.

1. Manuscript

General Instructions

Today, the use of remote sensing data as an ideal source of precision and speed of operation has become one of the most important means of data collection. In the meantime, radar remote sensing with the capability of capturing images in different weather conditions and throughout the day is becoming widespread. On the other hand, the use of radar polarimetric imaging systems has been widely considered [1] because the derived images can improve applications since they provide more distributive information about the effects of the image. Classification is one of the most important techniques for identifying and distinguishing ground-type classes that are widely used in the field of geosciences, including in determining vegetation, determining thermal heat islands, detecting alterations. Radar images classification is still interesting to researchers. Yakkekhani et al. (2014) [2] examined the use of the support vector machine (SVM) method with a variety of kernels for classification purposes of UAVSAR polarimetric data. In 2006, Lardeux et al. [3] proposed an SVM algorithm to categorize all polarimetric data and tested this method on P-band data. By using the Covariance matrix elements, they showed that the classification of the SVM is better in L band. Khosravi et al. (2014) [4] used a multiple classification systems (MCS) based on the SVM algorithm to classify hyperspectral images. In this research, a comparison was also made between the proposed system and the AdaBoost, Begging, and Randomized Forest (RF) methods.

In the previous paragraph, an overview of the research has been briefly described in a variety of classification methods. Although these studies have succeeded in classifying radar images, they focus on only one classification algorithm. Each of the classification methods has its own special features and applications. Many algorithms are presented for classifying polarimetric images. The most important of these are the K-nearest neighboring (KNN) methods and the SVM and RF algorithms. These three classification methods are recognized as the most suitable models for optimizing the process of classification of remote sensing images [5]. Because of the diversity of methods and the importance of classification when using radar data, it is necessary to examine different classification methods so that the users can choose the preferred methodology for classification. This research intends to examine the types of classification algorithms using UAVSAR radar data. Different types of distribution matrix elements are used for the production of the features. These algorithms used a special manner for producing aclassification map-based training data.

The polarization target decomposition is divided into four main categories [6]: the first category is based on the dichotomy of Kennaugh matrix that is included Yang, Huynen, Holm, and Brans. The second category is developed on the basis of the Covariance matrix C3 or coherent matrix of the Freeman Dong decomposition, Durden, and Yamaguchi methods. The third category is obtained on the basis of the eigenvector and eigenvalues of the covariance matrix (or coherence matrix). Some of these methods are used according to their application, such as Holm, Van, Cloud, Zyl and Could, Pottier, and Could. The fourth category of polarization target decomposition is related to the coherent decomposition of S scattering matrix. Some of these methods are Krogager, Cameron, and Touzi [6]. Due to, the presented types of algorithms such as Cloud Pottier, Freeman, Krogager, Van Zyl; presented to produce the features.

2. Proposed Method

2.1. Support Vector Machine

The support vector machine algorithm is one of the supervised training of pattern detection algorithms which was presented by a Russian mathematician called Vapnik in 1995, and its principles are based on the statistical training theory [7]. The main basis of this method is a linear classification of data, by taking safety margins into account, and is basically considered as a binary separator with the main goal of reaching the optimized hyper-plane to increase the boundary of two classes. If the data are not linearly separated, they are transmitted to a higher dimension space using nonlinear kernels, and a hyperplane is formed. Assume that p is a training datum defined as $\left(x_i.y_i\right)$, in which $x_i$ is an n-dimensional attribution vector, and $y_i \in \left\{-1.1\right\}$ is its tag. This hyper-plane is defined by Equation (1):

$$w^T\mathsf{\Phi }\left(x\right)+b=0$$

(1)

where w is the weight vector which is perpendicular to the intended hyper-plane, b is the bias vector which is a constant value, showing the distance between hyper-plane and origin, and $\mathsf{\Phi }\left(x\right)$ is a kernel to transfer the data to a higher dimension space. As discussed, the aim of this classification is to find a hyper-plane by maximizing the margin and minimizing the overall error of Equation (2).

$$\begin{gathered} min(\frac{1}{2}{\Vert w\Vert }^2+C{\displaystyle \sum }_{i=1}^k{\xi }_i) \\ subjectto:y_i\left(w\mathsf{\Phi }\left(x_i\right)+b\right)>1-{\xi }_i i=1,\dots ,k \end{gathered}$$

(2)

C is the adjusting parameter/factor that adjusts generalization. To consider the noise in the data and interruptions between training data, ${\xi }_i$ is used.

2.2. K-Nearest Neighbour (KNN)

KNN has been used in statistical estimation and pattern recognition. The training sample of c pairs of a random sample $\left(x_i.y_i\right)$, in which i = 1, 2, …, n and y takes {1, 2, …, n} values, can be defined as Equation (3):

$$\begin{gathered} train=\left\{\left(x_1.y_1\right), \left(x_2.y_2\right),\dots ,\left(x_c.y_c\right)\right\} \\ y=\left\{1, 2,\dots ,n\right\} \end{gathered}$$

(3)

where $y_i$ determines the class of $x_i$ among the c probable classes. For this reason, for classification, firstly the nearest neighbor $x^{\prime }$ of X is determined in the training samples (Equation (4)) [8].

$$d\left(x_i.y_i\right)=\sqrt{{\displaystyle \sum }_{r=1}^n{\left(a_r\left(x_i\right)-a_r\left(x_j\right)\right)}^2}$$

(4)

The popularity of this method ensues from two properties, i.e., simple application and determined error boundaries. However, high analytical load and high sensitivity to k values are some of its drawbacks. Therefore, the k values have a key role in this method. If k is too small, the algorithm is sensitive to noise, and if k is too large, it is possible that, among the nearest neighbors, a tag of other classes is entailed.

2.3. Random Forest Algorithm (RF)

The random forest algorithm is one of the recent methods of image classification invented by Breiman in 2001 [9], by developing the Bagging method. This method differs from Bagging in random feature selection. When creating a decision tree, RF firstly selects a random subset of features in each selection branch. The number of trees should be sufficient to fix the error rate [10]. The RF provides a more flexible classification, because of randomly selecting subsets for producing each decision tree [11].

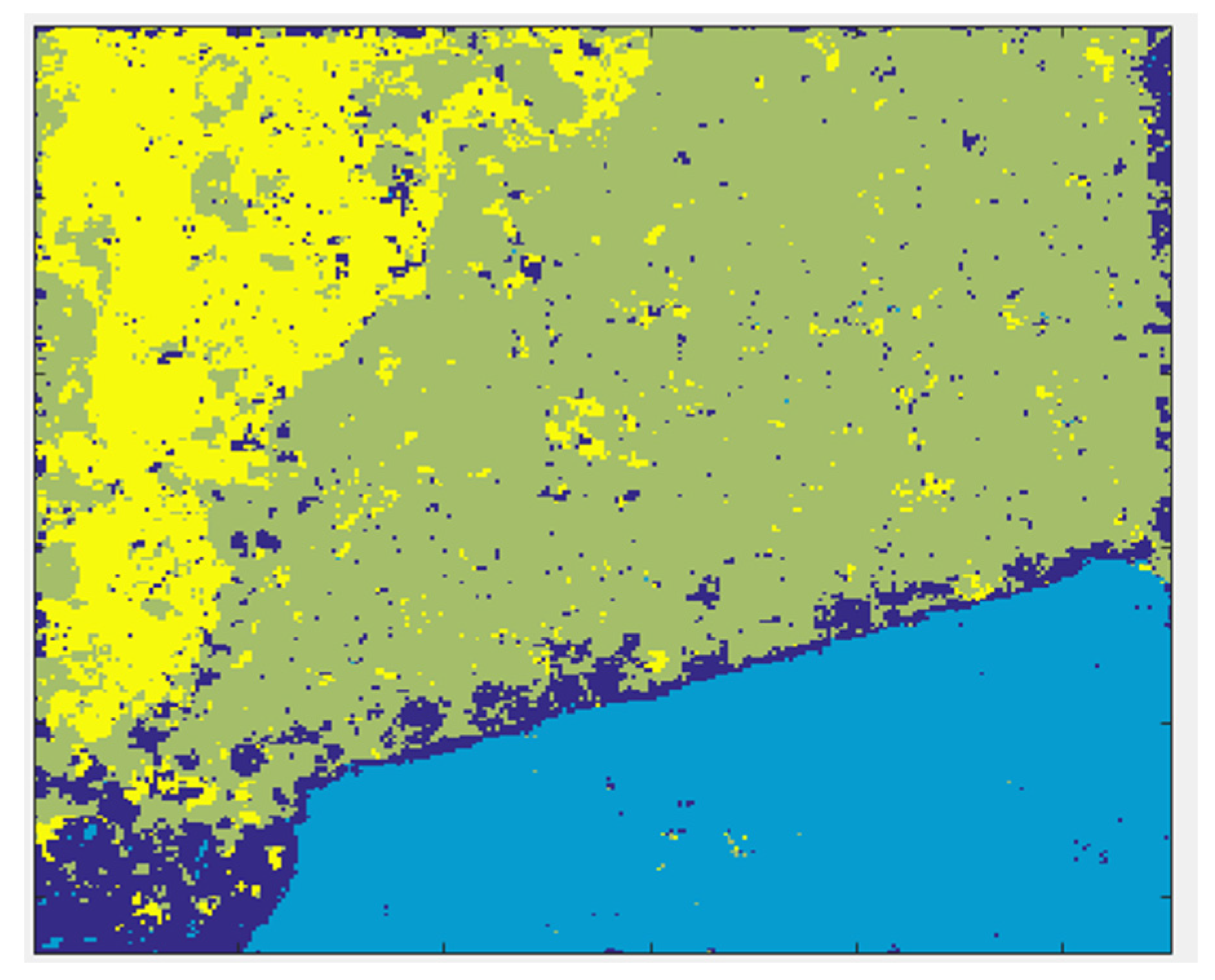
3. Study Area

The data which was used in this research was taken from full polarized data of Panama, the capital city of Panama, in South America. These data were collected on 6 February of 2010, by the UAVSAR Airborne system of the jet propulsion laboratory (JPL) institute of NASA. These images have with a spatial resolution of 1.6 m in each pixel. The dimension of this data is $12,756\times 12,773$ pixels. To reduce the data volume, and consequently reduce the calculation load, a subset with dimension of $276\times 266$ pixels including the urban area, water, and vegetation was selected. Figure 1 and Figure 2 show the related Pauli false color image and corresponding true color optical image of the considered region on Google Earth. Panama is located at 85°48′20″ W (−85.80556) and 30°10′36″ N (30.17667) geographical longitude and latitude, respectively. The considered region calculation load, a subset with dimension of $276\times 266$ pixels including the urban area, water, and vegetation, was selected. The considered region consists of three prominent classes: (1) water, (2) vegetation, and (3) urban area. A ground truth map was produced based on visual comparison and application of high-resolution Google Earth images (Figure 3).

4. Implementation

4.1. Extracted Decomposition Descriptors

To classify the polarimetric image, the decomposition descriptor was firstly extracted from the image in the PolSARpro_v4.2.0. To reduce the effect of speckle noise, a filter of $3\times 3$ size on the image for coherent target decomposition descriptors was used (

Table 1. Features extracted from decomposition.

Alpha anisotropy beta combination_1mH1mA combination_1mHA combination_H1mA combination_HA delta entropy gamma lambda Huynen_T11 Huynen_T22 Huynen_T33 Barnes1_T11 Barnes1_T22 Barnes1_T33 Barnes2_T11 Barnes2_T22 Barnes2_T33 Cloude_T11 Cloude_T22 Cloude_T33

Holm1_T11 Holm1_T22 Holm1_T33 Holm2_T11 Holm2_T22 Holm2_T33 Freeman_Dbl Freeman_Odd Freeman_Vol Freeman2_Ground Freeman2_Vol HAAlpha_T11 HAAlpha_T22 HAAlpha_T33 Krogager_Kd Krogager_Kh Krogager_Ks Neumann_delta_mod Neumann_delta_pha Neumann_psi Neumann_tau TSVM_alpha_s TSVM_alpha_s1

TSVM_alpha_s2 TSVM_alpha_s3 TSVM_phi_s TSVM_phi_s1 TSVM_phi_s2 TSVM_phi_s3 TSVM_psi TSVM_psi1 TSVM_psi2 TSVM_psi3 TSVM_tau_m TSVM_tau_m1 TSVM_tau_m2 TSVM_tau_m3 VanZyl3_Dbl VanZyl3_Odd VanZyl3_Vol Yamaguchi3_Dbl Yamaguchi3_Odd Yamaguchi3_Vol Yamaguchi4_Dbl Yamaguchi4_Hlx Yamaguchi4_Odd Yamaguchi4_Vol

).

4.2. Steps for Implementation

When the features used in decomposition algorithm were extracted, the resuting features were overlaid on each other to be applied to the classification algorithm. Using the ground optical image matched by radar images, the training and test data were randomly extracted. In this research, 30% and 70% of the values were devoted to the training and testing data, respectively. Figure 3 illustrates the ground truth map in three classes. Figure 4 presents the proposed method flowchart.

In this stage, the extracted features of the radar image were introduced as three different classifiers, including SVM, KNN, and RF. Consequently, the results of each classifier were examined and evaluated.

One of the supervised image classification methods in this paper is the KNN method. This classification was performed on a synthetic aperture radar (SAR) image with 70 extracted features. The results of the classification using visual and numerical algorithms were evaluated using an overall accuracy (OA) criteria.

The SVM method has a C parameter, and its kernel function, which is of the radial basis function (RBF) type, has a parameter γ, which needs to be optimized. For this purpose, a Grid search (GS) was used to determine its optimal values [12]. Also, the RF method has two parameters: the number of trees (N_tree) and the number of features in each tree (M_try); where necessary, their optimal values were determined.

Table 2. The optimal classification parameters.

Method	Parameter
SVM	C = 2	Γ = 2/4414 × 10−4
RF	Ntree = 100	Mtry = 8
KNN	K = 1	-

presents the optimal values of the parameters of the two methods mentioned.

The quantitative results from the use of the classification algorithms are shown in

Table 3. Classification performance accuracy.

Method	Overall Accuracy (%)
RF	88.65
SVM	77.38
KNN	73.29

. On the basis of the numerical results, it is clear that the RF algorithm has a higher degree of accuracy than the other two methods.

Figure 5, Figure 6 and Figure 7 show the visual representation of the algorithms used on the data. Similar to the numerical analysis, the visual result presenting the performance of the three of algorithms, show that the best is the RF algorithm.

5. Conclusions

SAR radar data, and especially all-polar data, are used as a relatively new and very useful source of information from the ground because of the features and benefits of the imaging process. In this paper, we examined the classification methods, including SVM, KNN, and RF, in order to compare them with respect to classification speed with appropriate accuracy. For this purpose, the entire polarized image was used in three major classes: urban area, vegetation, and water. After extraction of the characteristic features, each of the mentioned methods for the purpose of classification was applied to the data. The visual and numerical results from the classifications are presented in this study. The RF classification showed better classification accuracy than the other two methods. In addition, the RF classification method required less time to process the data than the other methods. The SVM method in the KNN methodology gave a better accuracy, but it required a high processing time due to the optimization of the parameters.