Evaluation of a Differentiation Scheme for Estimating Angular Acceleration from Angular Velocity †
Abstract
:1. Introduction
2. Materials and Methods
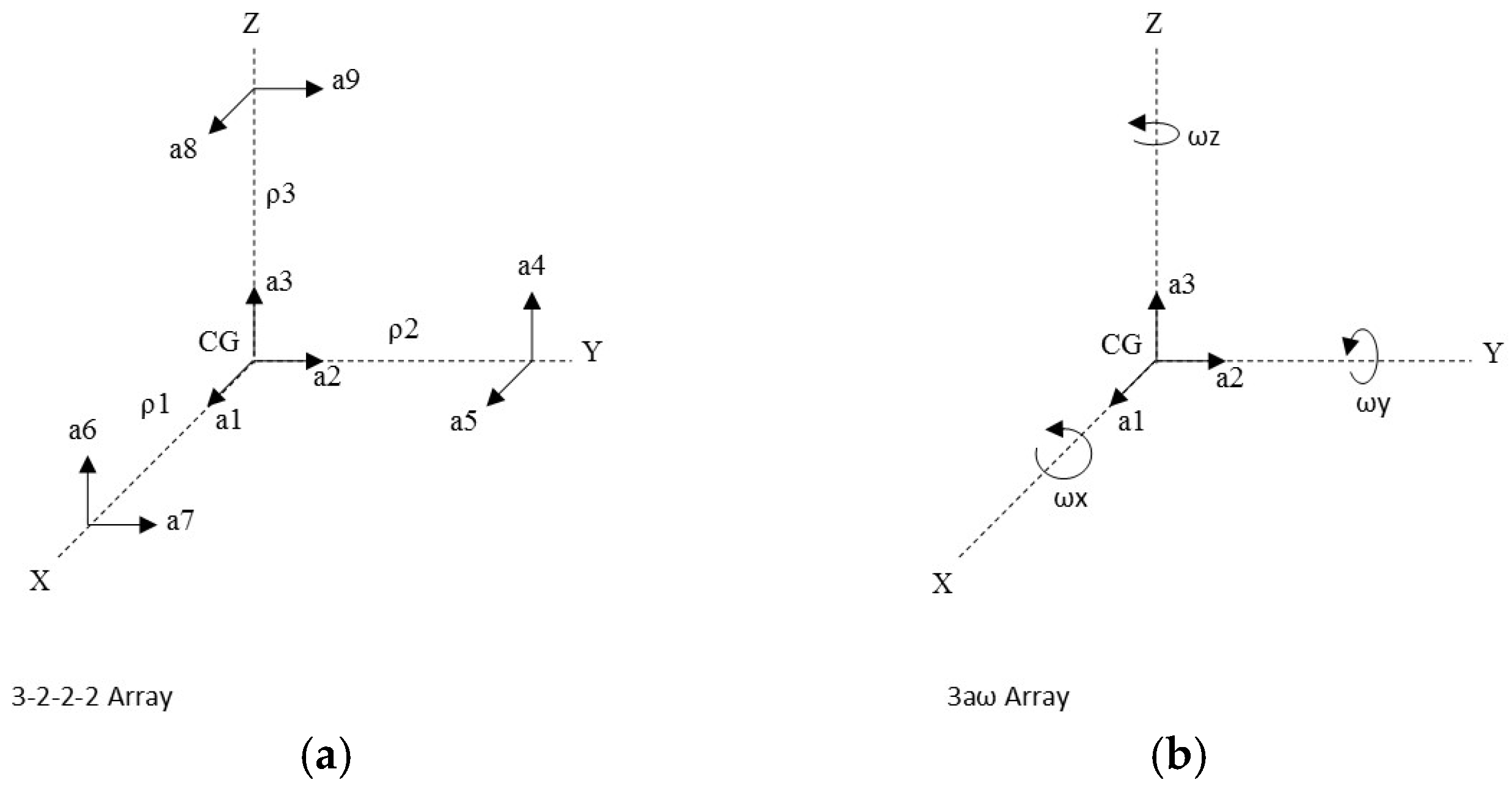
2.1. Data Collection
2.2. Data Analysis
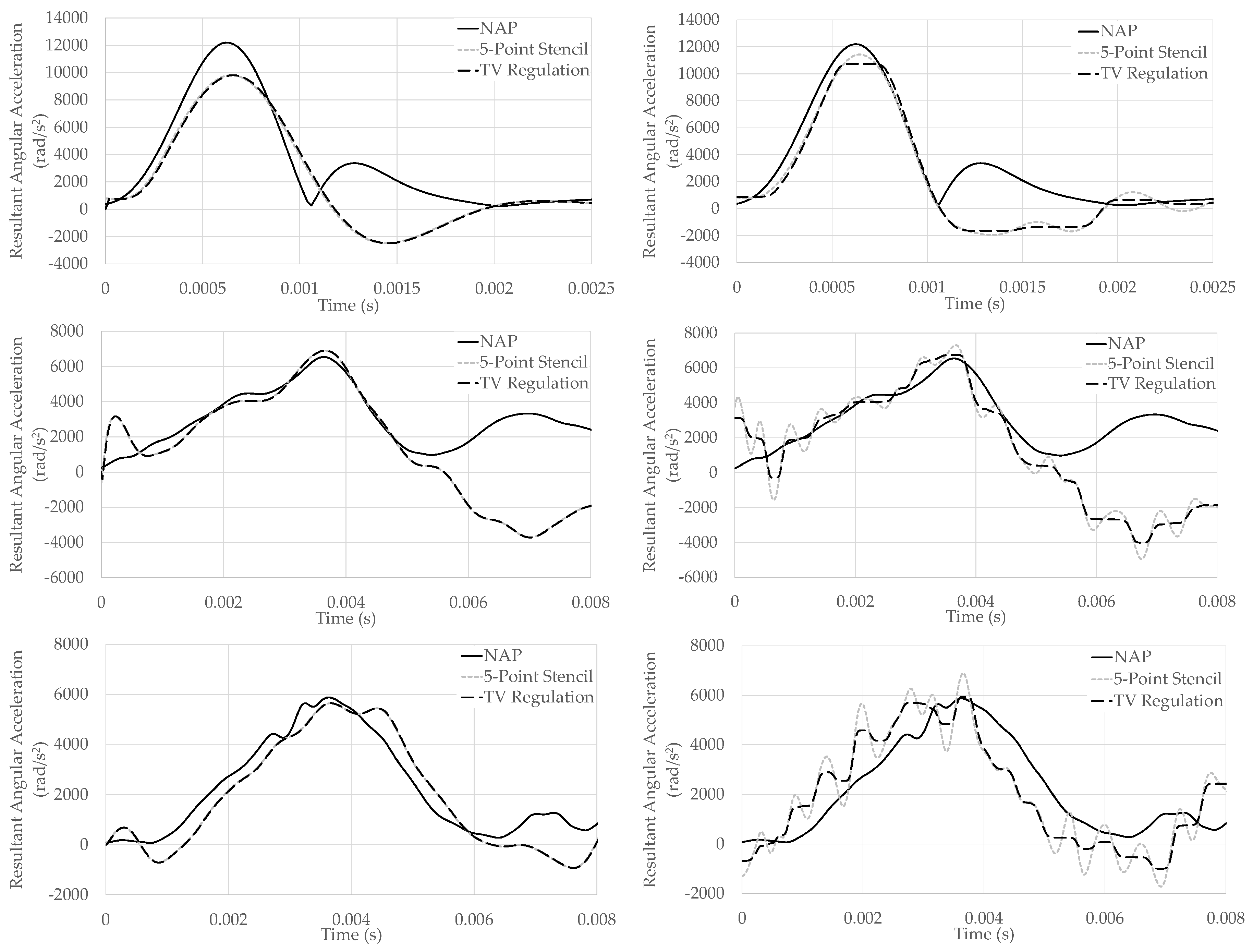
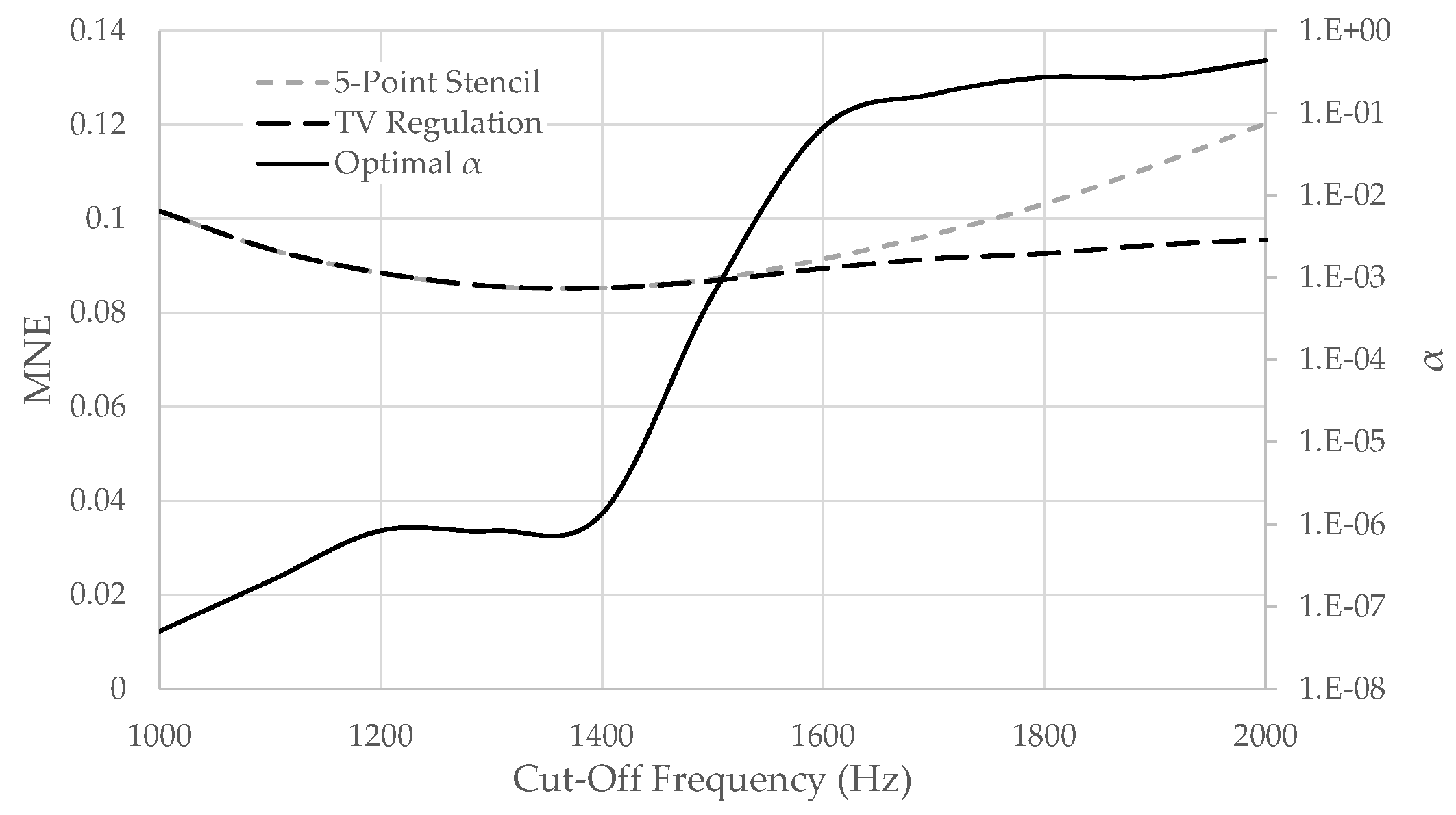
3. Results
4. Discussion
5. Conclusions
Conflicts of Interest
References
- Gadd, C.W. Use of a Weighted-Impulse Criterion for Estimating Injury Hazards. In Proceedings of the Tenth Stapp Car Crash Conference, Los Angeles, CA, USA, 8–9 November 1966. [Google Scholar]
- Newman, J.A. A generalized acceleration model for brain injury threshold (GAMBIT). In Proceedings of the International IRCOBI Conference on the Biomechanics of Impacts, Zurich, Switzerland, 2–4 September 1986. [Google Scholar]
- Newman, J.A.; Shewchenko, N.; Welbourne, E. A proposed new biomechanical head injury assessment function—The maximum power index. Stapp Car Crash J. 2000, 44, 215–247. [Google Scholar] [PubMed]
- Padgaonkar, A.J.; Krieger, K.W.; King, A.I. Measurement of angular acceleration of a rigid body using linear accelerometers. J. Appl. Mech. 1975, 42, 552–556. [Google Scholar] [CrossRef]
- Kang, Y.-S.; Moorhouse, K.; Bolte, J.H. Measurement of six degrees of freedom head kinematics in impact conditions employing six accelerometers and three angular rate sensors (6aω configuration). J. Biomech. Eng. 2011, 133, 111007. [Google Scholar] [CrossRef] [PubMed]
- Takhounts, E.; Eppinger, R.; Tannous, R.; Campbell, J.Q.; Power, E.; Shook, L.; Hasija, V. Analysis of 3D Rigid Body Motion Using the Nine Accelerometer Array System. Inj. Biomech. Res. 2003, 59–76. [Google Scholar]
- Bussone, W.R.; Bove, R.T.; Thomas, R.; Richards, D.; Prange, M.T. Six-Degree-of-Freedom Accelerations: Linear Arrays Compared with Angular Rate Sensors; SAE Technical Papers; No. 2010-01-1017; SAE International: Hong Kong, China, 2010. [Google Scholar]
- Laughlin, D.R. A Magnetohydrodynamic Angular Motion Sensor for Anthropomorphic Test Device Instrumentation; SAE Technical Papers; No. 892428; SAE International: Hong Kong, China, 1989. [Google Scholar]
- Martin, P.G.; Crandall, J.R.; Pilkey, W.D.; Chou, C.C.; Fileta, B.B. Measurement Techniques for Angular Velocity and Acceleration in an Impact Environment; SAE Technical Papers; No. 970575; SAE International: Hong Kong, China, 1997. [Google Scholar]
- Walker, J.A. Estimating velocities and accelerations of animal locomotion: A simulation experiment comparing numerical differentiation algorithms. J. Exp. Biol. 1998, 201, 981–995. [Google Scholar] [CrossRef]
- Chartrand, R. Numerical differentiation of noisy nonsmooth data. ISRN Appl Math. 2011, 2011. [Google Scholar] [CrossRef]
- National Operating Committee on Standards for Athletic Equipment (NOCSAE). Standard Test Method and Equipment Used in Evaluating the Performance Characteristics of Headgear/Equipment NOCSAE Doc ND 001-13m15c; NOCSAE: Overland Park, KN, USA, 2013; pp. 1–11. [Google Scholar]
- Kuo, C.; Wu, L.C.; Hammoor, B.T.; Luck, J.F.; Cutcliffe, H.C.; Lynall, R.C.; Kait, J.R.; Campbell, K.R.; Mihalik, J.P.; Bass, C.R.; et al. Effect of the mandible on mouthguard measurements of head kinematics. J. Biomech. 2016, 49, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.C.; Laksari, K.; Kuo, C.; Luck, J.F.; Kleiven, S.; Dale Bass, C.R.; Camarillo, D.B. Bandwidth and sample rate requirements for wearable head impact sensors. J. Biomech. 2016, 49, 2918–2924. [Google Scholar] [CrossRef] [PubMed]
- National Operating Committee on Standards for Athletic Equipment (NOCSAE). Standard Pneumatic Ram Test Method and Equipment Used in Evaluating the Performance Characteristics of Protective Headgear and Face Guards; NOCSAE: Overland Park, KN, USA, 2015; pp. 1–9. [Google Scholar]
- FIM. FIM Racing Homologation Programme for Helmets; FIM: Mies, Switzerland, 2017. [Google Scholar]
- Willinger, R.; Halldin, P.; Bogerd, C.P.; Deck, C.; Fahlstedt, M. Final Report of Working Group 3: Impact Engineering (COST Action TU1101/HOPE), Brussels, Belgium. 2015. Available online: http://publications.tno.nl/publication/34618465/RwBmO5 (accessed on 1 December 2017).


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nevins, D.; Petersen, P.; Smith, L. Evaluation of a Differentiation Scheme for Estimating Angular Acceleration from Angular Velocity. Proceedings 2018, 2, 271. https://doi.org/10.3390/proceedings2060271
Nevins D, Petersen P, Smith L. Evaluation of a Differentiation Scheme for Estimating Angular Acceleration from Angular Velocity. Proceedings. 2018; 2(6):271. https://doi.org/10.3390/proceedings2060271
Chicago/Turabian StyleNevins, Derek, Philip Petersen, and Lloyd Smith. 2018. "Evaluation of a Differentiation Scheme for Estimating Angular Acceleration from Angular Velocity" Proceedings 2, no. 6: 271. https://doi.org/10.3390/proceedings2060271
APA StyleNevins, D., Petersen, P., & Smith, L. (2018). Evaluation of a Differentiation Scheme for Estimating Angular Acceleration from Angular Velocity. Proceedings, 2(6), 271. https://doi.org/10.3390/proceedings2060271



