Dynamics of the Golf Club-Grip Interaction ^†

Abstract

A two degree of freedom hand-grip model was developed and simulated with a golfer downswing model, which contained an experimentally validated flexible shaft model. Experimental modal analysis was performed on a golf club to derive frequency response functions for both fixed-free and hands-free boundary conditions. Simulated frequency response functions were generated with the developed grip model to impose a hands-free boundary condition. Direct collocation using GPOPS-II was utilized to optimize the swing model with and without the grip model. An increase in clubhead velocity and decrease in shaft deflection was observed with the grip model implemented. In addition, the direct collocation approach resulted in similar joint angle trajectories, shaft deflection patterns, and joint torque profiles to those reported in the literature.

1. Introduction

Research in improving biomechanical models of golf swings is of great interest to the golf industry. By modeling the golf swing, insights can be made into how the golfer should swing the club and which improvements should be considered in golf club design. A recent review of previous golf swing models and simulations indicated that higher fidelity models, while not becoming overly complicated, have the best potential for furthering our understanding of golf swing dynamics [1]. Furthermore, the review suggests a need for more accurate representations of the grip and properties of the hand to understand the biomechanical interaction between player and club, as all current models define the club as being rigidly connected to the hand segment, providing zero additional degrees of freedom (DoF) [1]. Therefore, the objective of this project is to establish a hand-grip sub-model that can be implemented into a larger golf swing model for the first time.

Recent forward dynamic golf simulations use a parameter identification method to optimize the active torque produced by each joint in the golfer. The activation function for each joint is estimated by Equation (1), and was first utilized in a golf swing simulation by Mackenzie and Sprigings [2]

$${\mathrm{T}}_{\mathrm{pre}}\left(\mathrm{t}\right){=\mathrm{T}}_{\mathrm{m}}\left({1-\mathrm{e}}^{\frac{{\mathrm{t}}_{\mathrm{on}}}{{\mathrm{t}}_{\mathrm{act}}}}\right){-\mathrm{T}}_{\mathrm{m}}\left({1-\mathrm{e}}^{\frac{{\mathrm{t}}_{\mathrm{off}}}{{\mathrm{t}}_{\mathrm{deact}}}}\right),$$

(1)

where an optimal T_pre(t) is produced by selecting optimal parameters t_on and t_off. This method of determining optimal joint torques has been effective in producing similar results to actual golf swings [2,3,4]. It is of interest to compare the optimal control generated without a restriction on the threshold and frequency of activation that drives the joints in the model. This can be achieved through the use of a direct computational optimal control method implemented by GPOPS-II. GPOPS-II is a MATLAB software program that transcribes the dynamic optimization problem to a non-linear programming problem (NLP) using a Legendre-Gauss-Radau orthogonal collocation method [5]. In other biomechanical applications, direct collocation was found to be a promising improvement over other optimal control methods by increasing the computational efficiency of dynamic optimization [5]; it has yet to be used to maximize clubhead velocity in a forward dynamic golf swing simulation.

2. Materials and Methods

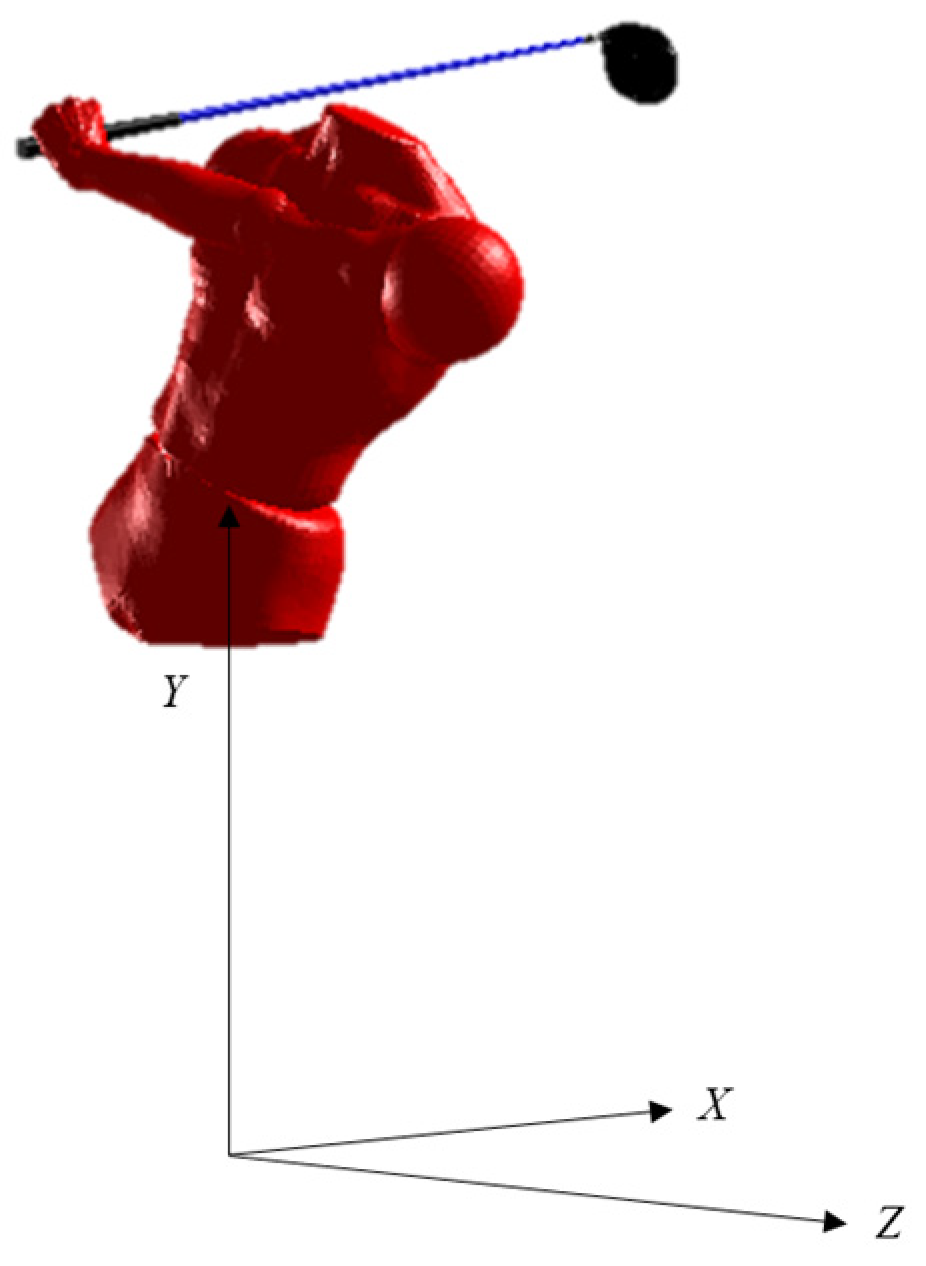
2.1. Golfer Model

In recent studies by Mackenzie and Sprigings [2] and Balzerson et al. [3], a four DoF golfer model incorporating a flexible club was shown to provide close comparison to experimental kinematics and kinetics of a low-handicap golfer. This model is represented in Figure 1. There are six bodies that are representative of human body segments, which are the lower, mid, and upper trunk, as well as the upper arm, forearm, and hand. Revolute joints between bodies represent the torso, shoulder, forearm, and wrist joints.

As with the model used in [2,3], the torso was inclined 30° to the vertical, and the swing plane of the arms was rotated 50° from the horizontal. Body segment inertial parameters matching another advanced biomechanics golfer model were used in this study, including location of the hips above the ground [4]. The clubhead and flexible shaft were modeled in the same way as in [3,6].

2.2. Grip Model

Previous studies to understand other hand-held equipment sports, such as tennis, have modeled the biodynamic interaction of the hand-grip similarly to a viscoelastically supported beam [7,8,9,10], which was typically described by rotational springs and dampers. Therefore, a two DoF hand model was created in this study to determine its effect on the dynamics of the downswing. This is represented by two revolute spring and dampers connecting the hand and shaft at the hand-grip location, providing an additional degree of freedom along the swing plane as well as one along the droop plane. The challenge of implementing the proposed grip model is the identification of the spring and damping parameters that best represent a hand’s grip on the club. An original method was implemented in this study to identify these parameters, and is discussed in the following section.

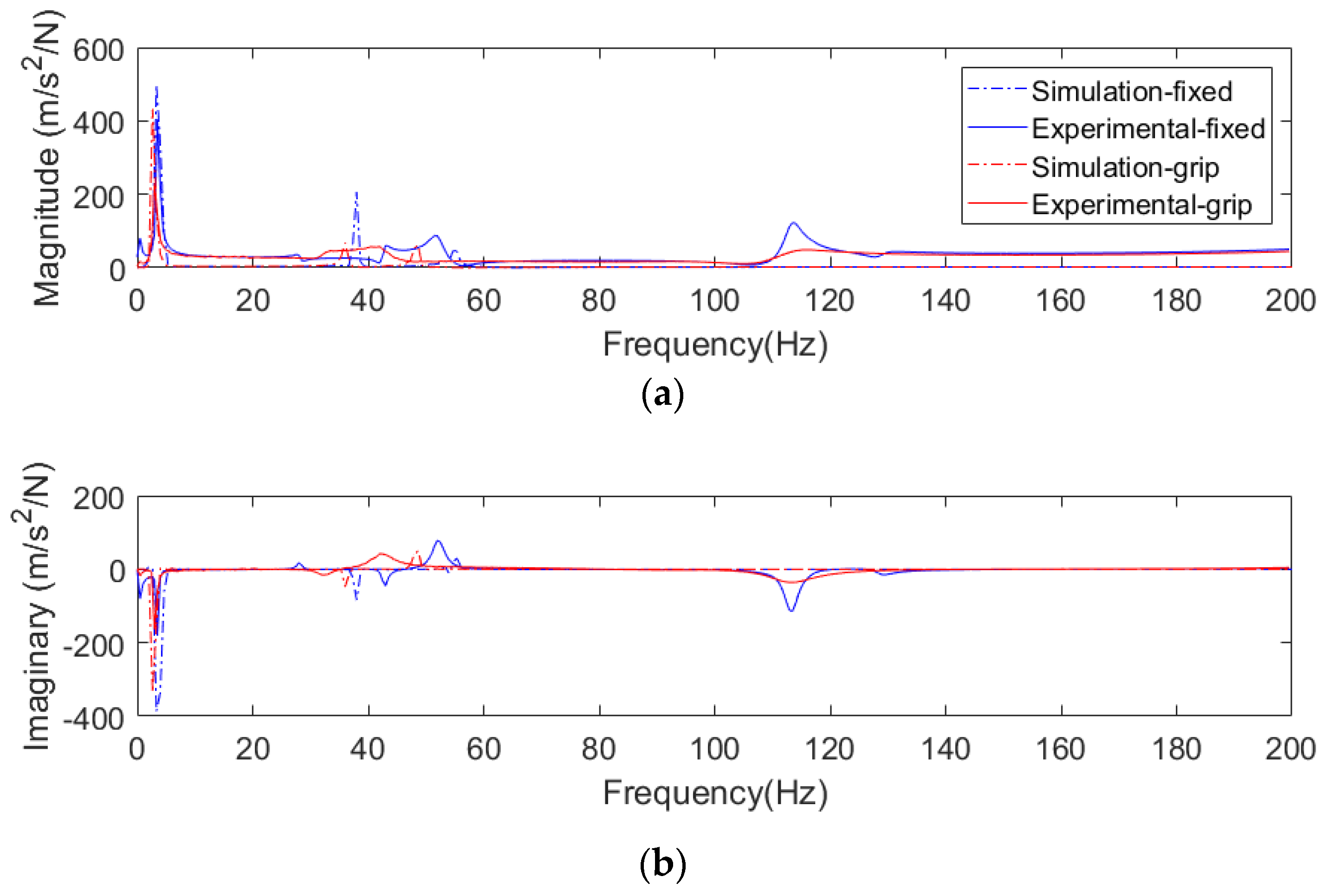
2.3. Modal Analysis

Two sets of experiments were performed to study the resulting vibration properties from fixed-free and hand-free boundary conditions imposed on a golf club of known stiffness properties. An impact hammer (Dytran, 5800B2) was used to excite the golf club with different frequency components. A single-axis accelerometer (Dytran, 3035BG, 2.5 grams, 8.3 mm, 50 g, 10,000 Hz) was positioned on the club 0.95 m from the butt end of the 1.075 m shaft. The impact hammer was struck at the center of the clubhead face, with five tests performed for each trial. The accelerometer was aligned perpendicular to the clubface plane, allowing for direct measurement in the coinciding excitation and swing plane. The input signal and response signal were fed to data acquisition hardware and exported to the CutPRO^® MaITF software package (Labview) for construction of the frequency response function (FRF). In the fixed-free boundary condition, the butt end of the club was fixed horizontally with a bench vice. The hand-free boundary condition was obtained by gripping the golf club in a one hand grip while resting on a table to allow the clubhead to be orientated in the same position as in the fixed-free case. Three trials were performed for each boundary condition.

Comparison of Experiment to Simulation

To obtain parameters for the grip model, simulations of the experimental set up of the fixed and hand-free boundary condition were established in MapleSim and exported to Simulink. The fixed-free boundary condition was modeled by a rigid connection between a fixed frame and the butt end of the shaft. For the hand-free boundary condition, the grip model was connected between a fixed-frame and the butt end of the shaft. Two bending coordinates were used in each transverse direction, and one coordinate was used for torsion. The force at the clubhead was input as normally distributed random numbers with a mean value of zero, variance of one, and sample time of 5 × 10⁻⁵, which allowed for the particular solution to be obtained for all frequency spectrums of the golf club. The steady-state acceleration response at each frequency was obtained by adding a 3 s delay to the simulation. The FRF was obtained in Matlab using the modalfrf function, in which Welch’s method and a 10,000-sample Hann window was used.

The first few modes of vibration were analyzed in the resulting FRF to obtain validity of the model, as suggested by a previous study which analyzed the frequency spectrum of golf clubs [11]. An internal damping element, which is input to the flexible beam model as a percentage of the Young’s modulus, was adjusted to allow for the closest comparison between the simulated and experimental FRF, which can be seen in Figure 2.

For the fixed-free boundary condition, bending modes in the simulated FRF are most easily identified by the imaginary plot, where the first three peaks occur at 3.3 Hz, 38.0 Hz, and 55.3 Hz. Similarly, the first three peaks of the experimental FRF occurred in a range of 3.5 Hz, 42.5–43.0 Hz, and 50.5–52.0 Hz. It was found that a MapleSim shaft damping value of 3 × 10^-5 was best able to match the amplitudes of the first three bending modes. An increased number of bending coordinates in the flexible beam model were necessary to provide a simulation that matched bending mode frequencies above 100 Hz, which also resulted in much longer simulation times.

Using the same beam parameters from the fixed-free case, the revolute spring and damping coefficients were selected so as to best match the first three bending modes of the experimental FRF for the hands-free boundary condition. A spring constant of 600 Nm/rad and damping coefficient of 0.05 Nms/rad in each revolute joint resulted in the closest comparison to the experimental bending modes. Symmetrical stiffness was assumed in each transverse direction. The first three peaks occur at 2.7 Hz, 35.3 Hz, and 48.7 Hz for the simulated FRF, and a range of 2.5–3.5 Hz, 32.5–34.0 Hz, and 40.0–43.5 Hz for the experimental FRF.

2.4. Optimization Method

Downswing simulations were generated with and without the grip model. The flexible beam model was modified to only allow transverse deflection in the swing and droop plane. The magnitude of torsion is minimal compared to the transverse deflection of the club, and therefore was not included in this model [2]. Joint torques were scaled by a force-velocity relationship of muscle, which has been incorporated into previous forward dynamic simulations of the golf swing [2,3,4,12].

$${\mathrm{u}}_{\mathsf{\omega }}{\left(\mathrm{t}\right)}_{\mathrm{i}}=\mathrm{u}{\left(\mathrm{t}\right)}_{\mathrm{i}}\frac{{\mathsf{\omega }}_{\max }-\dot{{\mathsf{\theta }}_{\mathrm{i}}}}{{\mathsf{\omega }}_{\max }+\mathsf{\Gamma }\dot{{\mathsf{\theta }}_{\mathrm{i}}}}.$$

(2)

Initial joint angles were similar to those used in [2,3]. As suggested by [4], a relative angle of 25° between the hand and shaft, in the same plane as the wrist joint, was used to provide a more reasonable grip orientation than the 0° value used by [2,3]. Furthermore, kinematic constraints were used to determine final joint angles to make contact with the golf ball. A tolerance of ±20° was placed on the final joint angles to account for shaft flexibility. In addition, joint torques were bound by the constraints found in [3]. In comparison to the activation torque function in Equation (1), it was found that the maximum torque available to each joint was obtained in the first 0.05 s of activation. This approximate Rate of Torque Development (RTD) compares closely to the shoulder RTD obtained from Bastian [13]. Although wrist RTD values were not provided in Bastian’s study, they were assumed to be in proportion to Equation (1). RTD values used were ±4000, ±3200 and ±1800 Nms⁻¹ for the torso, shoulder, and forearm and wrist joint, respectively.

Equations for the final clubhead speed and position were generated and represented as ChV and ChP in the inertial directions defined by Figure 1. The objective function minimized by GPOPS-II was

$$J=\frac{1}{QChV{X}_f^2}+R\left(ChP{X}_f^2+ChP{Y}_f^2\right)+S{t}_f$$

(3)

This performance index is similar to those found in other optimization swing studies [2,3,14]. The weighting $R$ used for minimizing the final clubhead position was relatively low, which allowed for flexibility of the optimal location the ball should be struck within an acceptable range.

To solve the dynamic optimization problem in GPOPS-II, the hp-LiuRao-Legendre variable polynomial order mesh method was employed, with a maximum of three mesh iterations and GPOPS-II mesh tolerance of 1 × 10⁻⁷. Furthermore, the IPOPT NLP software package was utilized to solve the resulting large-scale NLP with a relative tolerance of 1 × 10⁻⁵ and maximum iterations of 1000. A sparse derivative method was used to generate derivative source code for IPOPT.

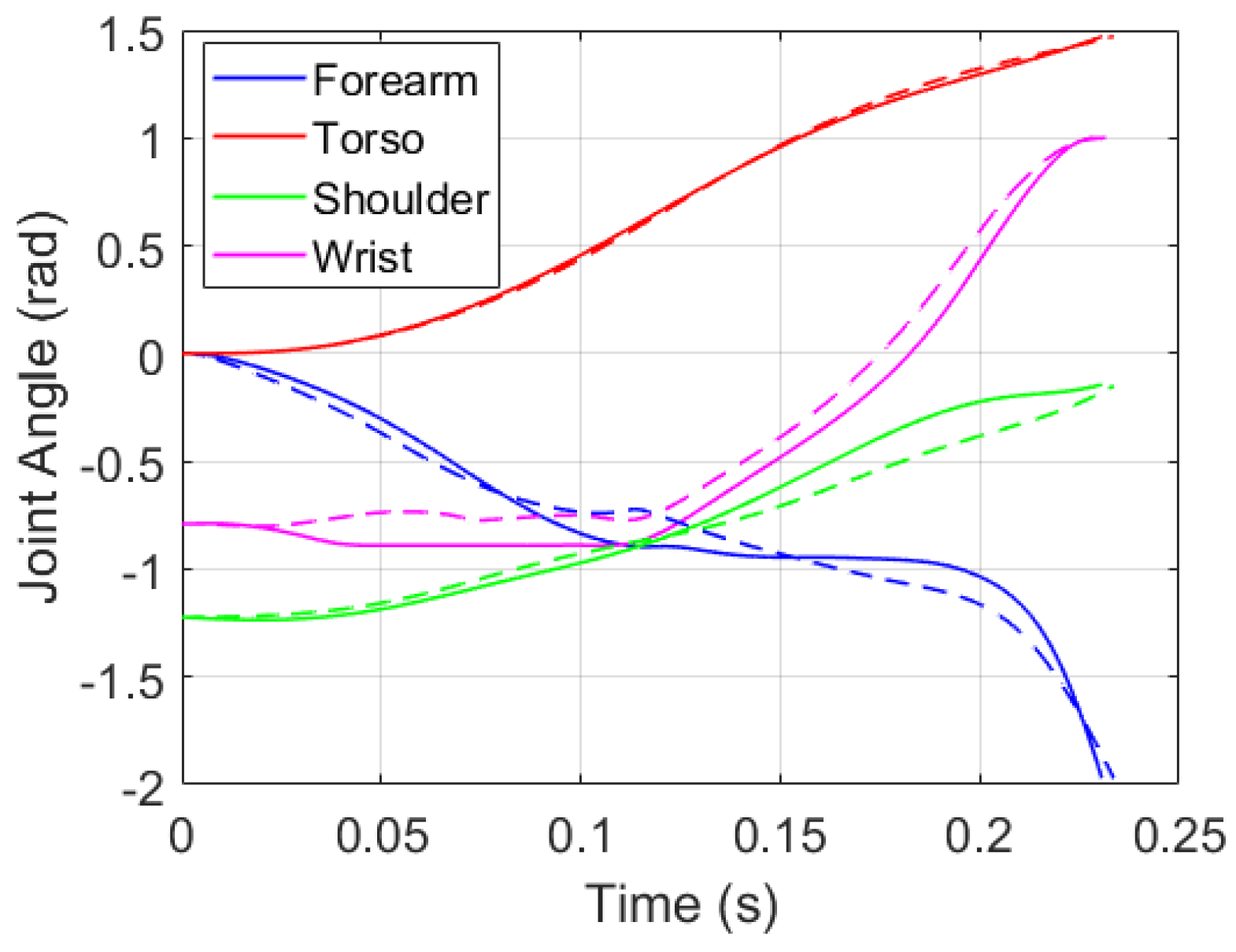
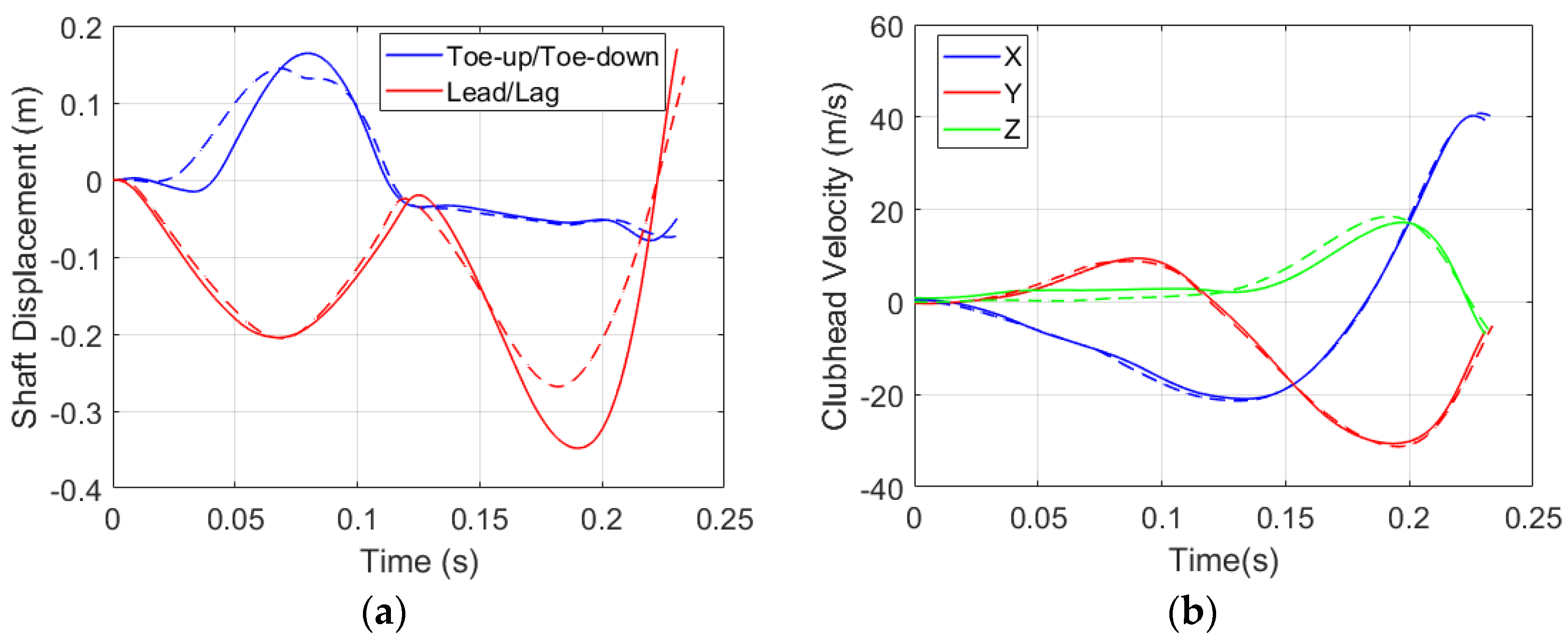
3. Results and Discussion

Figure 3 shows the optimal pre-scaled activation torque, ${\mathrm{u}}^{*}{\left(\mathrm{t}\right)}_{\mathrm{i}}$, as well as the optimal torque, ${\mathrm{u}}_{\mathsf{\omega }}^{*}{\left(\mathrm{t}\right)}_{\mathrm{i}}$, produced by each joint as a result of torque-velocity scaling. A solid line does not include the grip, and a dotted line includes the grip model.

In comparison to the pre-defined activation functions in [2,3], one major difference of the pre-scaled activation torque in Figure 3a is the initial activation of the shoulder, forearm, and wrist at the onset of the downswing. However, analyzing the subsequent activations for these joints show a similar sequence of activation to those determined using the pre-defined function, in which the torso remains activated throughout the swing, the shoulder activates next, which is followed by the forearm and wrist. In addition, the profiles of optimal torque between the optimization with and without the grip model are very similar, with the non-grip optimization producing slightly higher maximum torques.

The optimal trajectory of the wrist angle in Figure 4 shows that the wrist is held fixed at a constant angle until approximately 0.11 s into the downswing. From Figure 3b, the torque generated by the wrist joint is the torque required to maintain this constant angle. This is a well-known phenomenon in the biomechanics of a golf swing, and has been observed experimentally and through simulation in many previous studies [2,3,14,15].

Mackenzie and Sprigings state that the lead/lag deflection should reach its maximum value after the maximum toe-up deflection, and that the shaft should have positive lead at impact. In addition, the toe-up deflection is negative at impact [2]. As seen in Figure 5a, these shaft deflection characteristics found in a typical swing hold true. However, an additional lagging peak was obtained, which is a result of the initial activation of the forearm joint. Furthermore, when using the MapleSim shaft damping value of 3 × 10⁻⁵ obtained experimentally, oscillation of the shaft was observed similarly to the results obtained in [3], which is not found experimentally in literature [2]. To minimize this effect, a damping value of 1 × 10⁻² was necessary. The grip model appears to reduce the amplitude of the deflection in both the lead/lag and toe-up/toe-down directions. In comparison to literature, the maximum amplitudes of these plots appear at similar times; however, they are larger in magnitude (Mackenzie and Sprigings reported 7.3 cm maximum deflection).

The optimization including the grip model took 2842.0 s to perform, whereas the optimization without ran quicker in 1277.5 s. The optimal control and state trajectories produced a final clubhead speed of 40.0 m/s at 0.234 s with the grip model included, and 39.3 m/s at 0.231 s without. The clubhead speeds are similar to those produced by both Mackenzie and Sprigings and Balzerson et al., who obtained speeds of 41.9 m/s and 41.5 m/s [2,3].

4. Conclusions

In summary, a two-DoF grip model was developed and tuned for implementation in a four-DoF golf swing model. Performing the optimization using direct collocation allowed for the opportunity to observe how an optimized torque profile would compare to an optimized pre-defined single activation function [2,3]. Overall, this study found that the direct orthogonal collocation method using GPOPS-II can optimize a forward dynamic golf swing model. Further investigation into activation biomechanics are necessary, as initial torque activation and deactivation of the forearm produced shaft deflections not typically observed in a real golf swing. Moreover, the addition of the grip model required a substantial increase in simulation time, and produced relatively small differences in swing kinematics when compared to the results of a standard rigid grip implementation. Adjusting the stiffness and damping properties of the shaft may be a more efficient method of capturing the biodynamic effects of the grip. Future work should explore the effects the grip may have on additional phases of a simulated golf swing model, including the impact phase.