Abstract
The purpose of this study was to evaluate and compare various power output estimates and estimate anaerobic energy supply during treadmill roller-skiing. Roller-skiing sprint time-trial performance on a treadmill was compared to numerical simulations of three different power output estimates; non-inertial power estimate (NIP), inertial power estimate (IP), and optimization power estimate (OP). The OP was in best agreement with the measured speed of the skier. However, the IP was in better agreement with the measured finishing time of the real time trial, which may suggest that the IP better approximated the mean power than the other two estimates. Moreover, the NIP and IP are more simplistic than the OP and thereby more practical from a scientific standpoint. Based on this we recommend the use of the IP estimate.
1. Introduction
Power output is an important measure of performance in many locomotive endurance sports. In some sports, like cycling, power output can be measured easily with a power meter mounted on the bicycle. In other sports, such as cross-country skiing, power output is more complicated to measure. However, power output in cross-country skiing can be indirectly estimated based on a power balance model or by the external forces acting on a skier [1]. The same holds for roller-skiing on a treadmill, which is the main procedure for performance testing and scientific evaluation of cross-country skiers. Although a model based on power balance, or a motion equation based on external forces can be used to estimate power output, it is also applicable for simulating locomotive sports such as cross-country skiing. Moreover, by measuring the opposing forces of level road cycling, di Prampero [2] assessed the motion equation of a cyclist including the rolling resistance and the aerodynamic drag. Van Ingen Schenau et al. [1] further refined and generalized the model for all locomotive sports and included the rate of change of segmental energies. Furthermore, Bergh [3] introduced a power balance model for cross-country skiing which he used for allometric scaling analysis of cross-country skiing performance. Moxnes et al. [4] derived a motion equation, similar to Bergh’s power balance model [3], utilized for simulation and compared these results to GNSS-positioning data for an athlete performing cross-country skiing. In this study, physiological measurements and modeling were used to estimate metabolic power and power output for the simulations. Although the simulations showed greater variability than measured speed, the overall agreement between simulated values and measured speed was relatively good. Moxnes et al. [5] further utilized a power balance model to investigate the effect of aerodynamic drag and glide friction on performance in cross-country skiing. This study used another model based on physiological measurements, which resulted in better agreement with the measured speed. The time difference was ~13% between the model and the real performance of the skier [5]. In a third study, Moxnes et al. [6] made simulations using three different models of power output which were all functions of speed only.
Energy generation trough aerobic processes is considered the most important component to endurance performance [7]. However, it has been shown that anaerobic processes contribute substantially [7,8] during sprint races (3–4 min) and may be highly important for performance on variable terrain [7]. Nevertheless, indirect assessments of the anaerobic energetic component during whole-body exercise is associated with some difficulties [9]. The anaerobic energetic component during supramaximal roller-skiing can be estimated in several different ways [7,8], either by using the maximal accumulated oxygen deficit method [9] or a method based on gross efficiency [7]. A main problem with all previous methods employed for roller-skiing is that they have excluded the influence of instantaneous changes in inertia on the power output estimates during self-paced, time-trial roller-skiing [7,8]. No study has, to our knowledge, compared different power estimates and their corresponding anaerobic energetic components during supramaximal roller-skiing.
Therefore, the purpose of the current study was to evaluate and compare various power output estimates and the estimated anaerobic energy supply during treadmill roller-skiing.
2. Materials and Methods
Three different power output estimates were chosen for the validation purpose of the study: (a) the non-inertial power estimate (NIP); (b) the inertial power estimate (IP); and (c) the optimization power estimate (OP). After calculating the magnitude of each power estimate, they were evaluated by a mechanical model of treadmill roller-skiing. This mechanical model resulted in a pacing scheme that was compared to the real performance of a cross-country skier performing time-trial roller skiing on a treadmill.
2.1. Submaximal and Sprint Time-Trial Roller-Skiing Tests on the Treadmill
The experimental procedures and physiological data of the current paper originate from a previous study by Andersson et al. [7]. A Swedish male cross-country skier (age: 20 years, height: 173 cm, body mass: 73.7 kg, equipment mass: 3.6 kg) was randomly selected from the data set. All performance tests were conducted on a motor-driven treadmill designed for roller skiing (Rodby Innovation AB, Vänge, Sweden) according to Andersson et al. [7]. Respiratory variables were measured using an AMIS 2001 (Innovision A/S, Odense, Denmark) ergospirometry system. The rolling resistance of the roller skis was assessed as described previously by Ainegren et al. [10] and evaluated according to Andersson et al. [7].
The main performance test consisted of four sprint time-trials interspersed with 45 min of recovery. In the current investigation, only physiological data from the first sprint time trial (STT) was analyzed. The simulated 1300-m sprint course was 70% flat (1°) and 30% uphill (7°) with an overall average incline of 2.8° and a total climb of 64 m. This course consisted of five different sections, thereby four transitions. The participant used double poling on the three flat sections and diagonal stride on the two uphill sections (see course profile in Figure 1). Self-pacing was possible with the skier controlling the treadmill speed by adjusting the position on the belt. Two laser beams detected this position and increased (2.45 m·s−2) or decreased (1.44 m·s−2) the speed if the skier moved to the front or rear of the treadmill, respectively. Time was recorded every 10 m resulting in synced values for speed , along the course, as well as total completion time (finishing time) , when the STT was terminated. Prior to the STT, submaximal tests were performed to evaluate the impact of speed and incline on gross efficiency in double poling and diagonal stride. If gross efficiency was deemed to change with increasing speed or incline (r2 ≥ 0.5), linear or exponential regression analysis was used to estimate the sub-technique specific gross efficiency at the supramaximal speed during the STT. This was done by combining the regression equation for speed versus gross efficiency with the equation for the relative change in gross efficiency with incline (for details see Andersson et al. [7]).
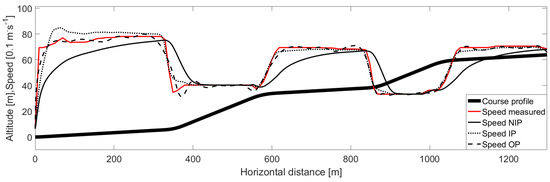
Figure 1.
The sprint time-trial course profile and speed profiles of the measured treadmill speed and the simulated speed of the various power estimates: Non-inertial power estimate (NIP), inertial power estimate (IP), and optimization power estimate (OP).
2.2. Power Output Estimates
All power output estimates in this study exclude the influence of air drag because a skier’s motion relative to ambient air is negligible on a treadmill. Furthermore, no power estimate in this study considers the rate of change of segmental energies of the skier because this internal power was not included in the gross efficiency calculation. All models were programmed into Matlab R2016a (Mathworks, Natick, MA, USA).
The NIP estimate is the result of power balance in the absence of acceleration. Therefore, only gravity and rolling resistance are included. The NIP estimate is expressed as:
where is the speed in the direction of treadmill motion during the treadmill roller-skiing, is the total mass of the skier and his/her equipment, is the acceleration of gravity, is the treadmill inclination angle (uphill is positive, is horizontal), and is the coefficient of rolling resistance between the roller-skies and the treadmill belt.
The IP estimate is also the result of power balance but in this estimate acceleration is accounted for. Therefore, inertial resistance compliments gravity and rolling resistance. The IP estimate is expressed as:
where is the rate of change of speed in the direction of treadmill motion (scalar component of acceleration). This acceleration was estimated from the measured speed as an average between the measured values.
The OP estimate is based on the numerical optimization model of Sundström et al. [11] which is based on the same mechanical model as Carlsson et al. [12]. The OP estimate uses the method of moving asymptotes [13] and varies the power output to minimize the square of speed difference between the mechanical model and the actual performance of a cross-country skier on a treadmill. The OP estimate is expressed as:
where is the simulated speed at equally spaced positions along the course, and is the measured speed during the time-trial sprint.
The anaerobic energy expenditure was calculated as the difference between total energy expenditure from each power estimate and the total aerobic energy expenditure computed from oxygen uptake () during the STT:
where is the power output estimate (Equations (1) and (2) and the result of Equation (3)), is the gross efficiency, is the rate of oxygen consumption (L·min−1) at standard temperature and pressure, is the measured respiratory exchange ratio and is the measured time between and + 1. was set to 1.00, assuming a 100% carbohydrate oxidation during the STT.
2.3. Evaluation Model
The evaluation model is based on the same numerical simulation approach as the OP estimate [12]. The STT was simulated by solving the motion equation of roller skiing with the power output estimates as input data. This approach gives estimates of both the finishing time and the speed variations along the course.
The motion equation was dived into two coupled nonlinear ordinary differential equations and solved numerically by the Runge-Kutta-Fehlberg Method [14]. Matlab R2016a was used for the motion equation solution and the calculations of accumulated anaerobic energy expenditure, time difference, and mean speed difference.
3. Results
Based on the actual test-results from the participating skier, submaximal gross efficiency during diagonal skiing was independent of speed and was on average 19.9%, while gross efficiency (GE) during double poling decreased linearly (r2 = 0.88) at high submaximal speeds according to the following regression equation; . The gross efficiency was observed to be dependent on incline in both diagonal skiing (r2 = 0.95) and double poling (r2 = 0.93), with regression equations of and for diagonal skiing and double poling used to predict the relative change in gross efficiency from the reference inclines of 1° and 7°, respectively. The skier’s real finishing time during the STT was measured to 239.2 s, an average speed of 5.43 m·s−1, and an average of 3.8 L·min−1, which corresponds to a total aerobic energy expenditure of 316.6 kJ. The peak during the STT was 4.6 L·min−1.
The speed variation of the various power estimates and the measured values are presented in Figure 1. The corresponding power distributions and accumulated anaerobic energy expenditures can be seen in Figure 2. All simulations underestimated time and the difference in time between the real performance and the simulations were 7.0, 0.39, and 1.5% for the NIP, IP, and OP respectively. Furthermore, the root of the mean squared speed difference between the real performance and the simulations were 1.13, 0.44, and 0.30 m·s−1 for the NIP, IP, and OP respectively. The various power estimates resulted in total generated work of 69.1, 70.0, and 69.1 kJ for the NIP, IP, and OP respectively when the measured time of the STT was considered. The corresponding anaerobic energy expenditures were calculated to 72.1, 102.4, and 85.2 kJ for the NIP, IP, and OP respectively.
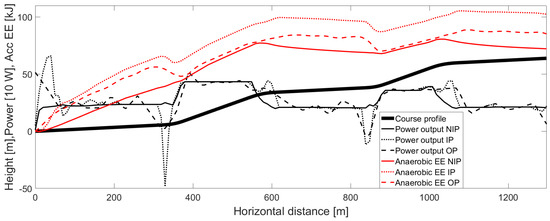
Figure 2.
The sprint time-trial course profile, power output distributions, and accumulated anaerobic energy expenditure (EE) profiles of the various power estimates: Non-inertial power estimate (NIP), inertial power estimate (IP), and optimization power estimate (OP).
4. Discussion
The various models showed differing accuracy regarding the estimation of finishing time. The IP and OP estimates showed to be more accurate than the NIP estimate while the IP estimate also showed a slight advantage in regards to the OP estimate. As it seems, both NIP and OP underestimated the mean power output and therefore overestimated the finishing time of the skier. However, regarding the mean speed difference, the OP estimate showed to be slightly more accurate than the IP estimate and much more accurate than NIP estimate.
The IP simulation accurately predicted the finishing time, but lacks when it comes to the accuracy of the speed profile. Figure 1 shows that the IP speed differs substantially from the measured speed in the flat sections and during the transition between sections. This might be due to the way acceleration was calculated in the IP estimate (i.e., as a mean over 10 m). The speed difference of the IP estimate may be reduced by a smooth spline function for speed that can be differentiated to obtain the instantaneous acceleration. Another way to improve these results would be to use more densely distributed data points that may reduce truncation errors. In a similar manner, the OP could better estimate the power output if the number of optimization variables are increased which would facilitate more rapid changes in the calculated power output and thereby enabling more rapid changes in acceleration. In the comparison between the IP and OP estimates, the IP estimate is more simplistic and therefore more attractive from a scientific standpoint. In comparison to our findings, Moxnes et al. [6] reported a best fit root of sum squared difference for their models of ~2.81, which corresponded to a root mean squared value of ~0.78 m·s−1 for the average speed of the 13 splits along their course. This value might be compared to the root mean squared speed difference of 1.13, 0.44, and 0.30 m·s−1 for the NIP, IP, and OP respectively. However, the model of Moxnes et al. [6] simulated cross-country skiing on snow instead of roller-skiing, which is more difficult because of varying environmental conditions, such as gliding friction and ambient wind.
During the STT testing, the initial treadmill speed (i.e., pre-set speed) during the transitions from flat to uphill terrain was programmed to decrease before entering the uphill so that the skier would not fall off the rear of the treadmill because of high speed and a steep uphill incline. The skier countered this by firstly coasting forward on the treadmill as belt speed decreased and thereafter coasting rearwards back to the original position again when incline increased enough. The models did not consider this motion and therefore assumed that the skier had no motion relative to the surrounding of the treadmill. Because of this assumption and inertia, the IP and OP resulted in low power (or negative, braking power) to decelerate in the transitions from flat to uphill (Figure 2). Therefore, a negative accumulation of anaerobic energy expenditure (i.e., “anaerobic” recovery) could be observed during these parts of the STT course. This disregard of motion relative to the surrounding would probably not have a substantial effect on the validity of the anaerobic energy expenditure because both deceleration from braking and coasting will have equivalent effects on the estimated anaerobic energy expenditure (Equation (4)).
Figure 2 shows that the various power output estimates resulted in different total anaerobic energy expenditures. Concerning the overestimation of finishing time in the NIP and OP estimates, it is reasonable that these models underestimated the total anaerobic energy component.
5. Conclusions
Although we conclude that the IP and OP estimates give acceptable power output estimates for treadmill roller skiing sprint time-trials, there are several ways to refine both estimates. We recommend the use of the IP estimate considering that it is more simplistic than the OP model. Moreover, the NIP estimate is non-satisfactory for treadmill roller skiing sprint time-trials due to its disregard of inertial influence.
Acknowledgment
The European Regional Development Fund of the European Union supported this work.
References
- Van Ingen Schenau, G.J.; Cavanagh, P.R. Power equations in endurance sports. J. Biomech. 1990, 23, 865–881. [Google Scholar] [CrossRef]
- Di Prampero, P.E.; Cortili, G.; Mognoni, P.; Saibene, F. Equation of motion of a cyclist. J. Appl. Physiol. 1979, 47, 201–206. [Google Scholar] [CrossRef] [PubMed]
- Bergh, U. The influence of body-mass in cross-country skiing. Med. Sci. Sport Exer. 1987, 19, 324–331. [Google Scholar] [CrossRef]
- Moxnes, J.F.; Hausken, K. Cross-country skiing motion equations, locomotive forces and mass scaling laws. Math. Comp. Model. Dyn. 2008, 14, 535–69. [Google Scholar] [CrossRef]
- Moxnes, J.F.; Sandbakk, Ø.; Hausken, K. A simulation of cross-country skiing on varying terrain by using a mathematical power balance model. Open Access J. Sports Med. 2013, 4, 127–139. [Google Scholar] [CrossRef] [PubMed]
- Moxnes, J.F.; Sandbakk, Ø.; Hausken, K. Using the power balance model to simulate cross-country skiing on varying terrain. Open Access J. Sports Med. 2014, 5, 89–98. [Google Scholar] [CrossRef] [PubMed]
- Andersson, E.; Björklund, G.; Holmberg, H.C.; Ørtenblad, N. Energy system contributions and determinants of performance in sprint cross-country skiing. Scand. J. Med. Sci. Sports 2017, 27, 385–398. [Google Scholar] [CrossRef] [PubMed]
- Losnegard, T.; Myklebust, H.; Hallén, J. Anaerobic capacity as a determinant of performance in sprint skiing. Med. Sci. Sports Exerc. 2012, 44, 673–681. [Google Scholar] [CrossRef] [PubMed]
- Noordhof, D.A.; de Koning, J.J.; Foster, C. The maximal accumulated oxygen deficit method: A valid and reliable measure of anaerobic capacity? Sports Med. 2010, 40, 285–302. [Google Scholar] [CrossRef] [PubMed]
- Ainegren, M.; Carlsson, P.; Tinnsten, M. Rolling resistance for treadmill roller skiing. Sports Eng. 2008, 11, 23. [Google Scholar] [CrossRef]
- Sundström, D.; Carlsson, P.; Ståhl, F.; Tinnsten, M. Numerical optimization of pacing strategy in cross-country skiing. Struct. Multidiscip. Optim. 2013, 47, 943–950. [Google Scholar] [CrossRef][Green Version]
- Carlsson, P.; Tinnsten, M.; Ainegren, M. Numerical simulation of cross-country skiing. Comput. Methods Biomech. Biomed. Eng. 2011, 14, 741–746. [Google Scholar] [CrossRef] [PubMed]
- Svanberg, K. The method of moving asymptotes: A new method for structural optimization. Int. J. Numer. Methods Eng. 1987, 24, 359–373. [Google Scholar] [CrossRef]
- Fehlberg, E. Low-Order Classical Runge-Kutta Formulas with Stepsize Control and Their Application to Some Heat Transfer Problems; NASA Technical Report; NASA Marshall Space Flight Center: Huntsville, AL, USA, 1969. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).