Abstract
Using multiple cameras with force platforms is a classical and popular method for gait analysis. However; it is difficult to measure natural walking; because the subjects have to adjust their steps to place on the force platform. This study proposes two rigid body linked segment models to estimate the joint force and ground reaction force without force platform. In order to validate the accuracy of the models; the authors compared their kinetic parameters with those of classical model. The results showed that the proposed models could estimate the ground reaction force and the joint force with high accuracy (less than 10% in the third quartile on all axes). In addition; using the center of pressure from force platform could also estimate the joint torque with high accuracy. These results suggest that we can analyze the gait without force platform; if the center of pressure is provided in the future.
1. Introduction
In order to analyze human gait, combination of optical cameras and force platforms is a popular and classical method in biomechanics. When the experimenter forces subjects walk in the laboratory, it is difficult for them to step onto the force platforms in their natural walk. Usually, they have to adjust their step length for the pre-defined force platform alignment. Some of previous studies had measured the pressure distribution or estimated a vertical component of ground reaction force using a pressure sensor on the floor or attached pressure sensors underneath the shoes. However, in those studies, since the pressure sensor could output only vertical force component, it is not sufficient for the kinetics approach [1,2]. Recently, motion capture system with/and miniature inertia sensor device has been reported in the field of medicine and rehabilitation. However, most of the cases, physiotherapists’s assessment has been limited for the kinematical issue not for the kinetics one [3,4]. Since, the kinematics is the result of the motion, from the viewpoint of the causal association, the cause of the motion is obviously muscular force and external force acting to the human body. Therefore, for the deep insight of the walking, kinetic approach must be necessary. Thus, the purpose of this study was to propose a gait analysis methodology which is force platform free and validate the accuracy of its result of the kinetics comparing to the classical model.
2. Rigid Body linked Segment Model
2.1. Classical Rigid Body Linked Segment Model for Lower Limbs
A classical rigid linked segment model is only for lower limbs (Model A) (Figure 1 left). In order to identify segment’s joint forces and torques on the stance leg, this classical model requires ground reaction force by the force platforms.
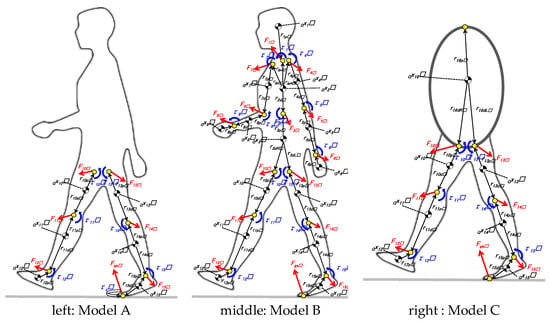
Figure 1.
Rigid body linked segment models.
2.2. Full Body Rigid Body Linked Segment Model without Force Platform
For the full body rigid linked segment model (Model B), the authors divide human body into 15 segments, then solve the equations of motion from the terminal segments except stance side lower limb (Figure 1 middle). An advantage of Model B is to allow us to solve the joint force and torque without using force platforms. A disadvantage is that it is impossible to solve joint forces and torques during the double supporting period.
2.3. Upper Body Abbreviated Rigid Body Linked Segment Model without Force Platform
A full body rigid linked segment model abbreviating the upper body (Model C) is our second proposed model (Figure 1 right). The authors suppose segments of upper body as one single segment. An advantage of this model is that we can reduce the number of segments for the calculation, then it leads us to reduce reflective markers in the experiment. On the other hand, a disadvantage of this model is that the integration process for upper body segments into one single mass might be over or under estimation of the total upper body kinetics in asymmetry motion.
For all models, the inertial parameters were referred Ae [5] and Okada [6].
3. Experimental and Analysis Method
Motion Capture System (Vicon MX T-20) and force platforms (Kistler, 9281C) were used. Nine volunteer elders (71.6 ± 7.2, 5 males, 4 females) were recruited for this study. Subjects walked in the laboratory setting condition which had 5 m straight course with two platforms. They were asked to walk naturally. Then three to four successful data which the subjects were able to place their steps on the force platform were analyzed.
The authors examined only one single supporting period by three different models. For the assessment of the difference between models, we examined absolute value of the difference D, D = |A(t) − B(t)|, and the ratio of the difference E, E = |A(t) − B(t)|/|Max(A) − Min(A)| × 100 (%). Here A(t) is the “standard time series” and B(t) is the “comparing time series”. In this study, we used the classical model (Model A) as A(t) and compared proposed Model B and Model C as B(t).
This study was approved by Keio University Shonan Fujisawa Campus ethics committee in 19 May 2016.
4. Results
The joint forces on the hip were calculated by three different models with respected to the local coordinate system of the thigh. Figure 2 shows examples of hip joint forces calculated by three models during one single walking cycle. In Figure 2, time series of Model A, Model B and Model C show similar pattern during their single supporting period in both sides. Axis-I and Axis-J in the figures are the medio-lateral and antero-posterior axis respectively. Then Axis-K was along with the longitudinal axis of the segments.
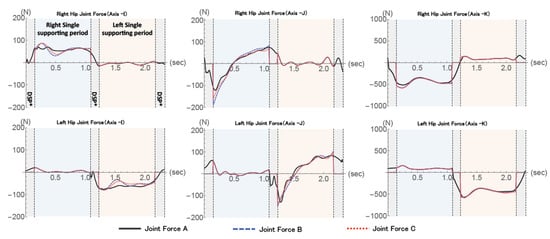
Figure 2.
Comparison of Hip joint force. * DSP: Double supporting period.
The absolute difference between Model A and Model B was less than 50 N and its median is about 14 N in Axis-K, which is along with the longitudinal axis of the thigh. As for other axes, the medians of absolute deviations were less than 10 N. On the other hand, the ratio of the difference shows less than 3% in Axis-K. It means that the magnitude of the joint force on Axis-K in hip was remarkably larger than others. Conversely, the absolute difference of the joint force component on Axis-I and Axis-J were smaller than that of Axis-K, but its difference ratios were larger than Axis-K’s one. Similarly, largest absolute difference between Model A and Model C can be seen also in Axis-K, and its ratio of difference is smallest.
Figure 3 shows the hip joint torques calculated by three models. We can see large deviation of the magnitude of joint torque on Axis-I (Flexion/Extension) rather than those of Axis-J and Axis-K. Although, Model B and Model C could estimate ground reaction force with high accuracy in the single supporting phase. Therefore, the location of the center of pressure should be identified for our further investigation. Nishikawa [7] mentioned that free moment can be small enough to neglect in case of walking. Therefore, the authors decided to neglect free moment in this study and calculate the joint torques of lower limbs. is the ground reaction force calculated by Model C without force platforms. Then, in order to improve accuracy of the torque estimation, we calculated joint torques (Joint Torque D) of the lower limbs using the center of pressure measured by the force platforms and the ground reaction force by calculated by Model C (abbreviated upper body model) . Figure 4 shows the estimated result of the hip joint torque, Joint Torque D. While there had been remarkable deviation of the hip joint torque between Model A and Model B/Model C (Figure 3), Figure 4 shows that the results of this stepwise estimation with the location of the center of pressure was improved.
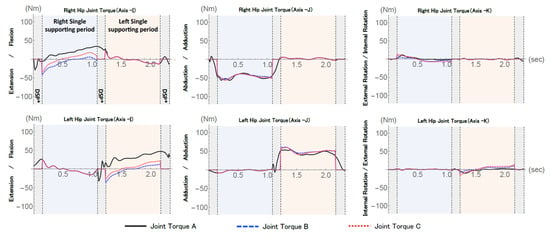
Figure 3.
Comparison of Hip joint torque. * DSP: Double supporting period.
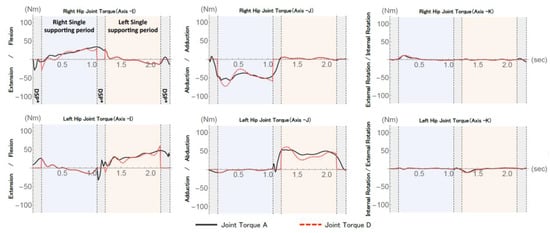
Figure 4.
Comparison of Hip joint torque. * DSP: Double supporting period.
5. Discussion
Model A, the classical inverse dynamics model of lower extremities used the ground reaction force and its location of the center of pressure for the external moment by the ground reaction force. Then we calculated joint forces/torques of single supported stance leg from the foot segment toward hip joint. In general, this procedure has been believed the gold standard method in the biomechanics [8]. In this study, in order to validate accuracy of the results of Model B, full bodied inverse dynamics and Model C, full, but abbreviated upper bodied inverse dynamics model, we evaluated the deviation of the calculated forces/torques between Model A versus Model B, Model A versus Model C. In general tendency, both of Model B and Model C could well estimate the joint forces and torques. However, the magnitude of those errors was depending on the segment axis. The largest error can be seen in Axis-K, which is along with the longitudinal axis of the lower extremity. Axis-I and Axis-J are the antero-posterior and medio-lateral axis of the thigh respectively. Since those axes’ component of the load were much lower than that of Axis-K, the maximum error was always shown in the Axis-K. However, the ratio of error was smallest in Axis-K conversely. The authors recognize several causes for those errors which deviated from the Model A. Both of proposed model, Model B and Model C require the sequential calculation of the equation of the motion from the distal end segments of the upper extremities, head or abbreviated upper trunk. In those calculation process, the accumulated errors might result in the total error. Since our validation between three models used same obtained motion capture data set, the error cause should be model dependent. For example, the estimation of the moment of inertial of the composite segments. At this moment, we could not identify a concrete error reason.
However, even though the gait cycle of the subjects were fluctuated 10 to 20% within the experimental trials, the mean error ratio was less than 10%. In addition, the errors and its ratio of Model B and Model C were almost the same. Thus, the authors can propose that Model C is the appropriate and convenient model for the real gait analysis situation because of its simple setting. At this moment, we could not identify a precise reason of the deviation of the hip joint torque on the single supporting leg between Model A and Model B/Model C, while the joint forces were well predicted.
In order to solve those error in the joint torques, we examined hip joint torque of the single supporting leg by the classical lower body model (Model A) with estimated ground reaction force by the Model C and the center of pressure location which was measured by the force platforms. The calculated hip joint torque result was improved rather than those of the results by Model B and Model C (Figure 3). Therefore, if we took the incremental steps from the abbreviated upper body model (Model C) for the ground reaction force estimation, then the classical lower body model (Model A) with only the location of the center of pressure, the joint torques can be well estimated. Thus, the alternative of the force platform, such as the precise pressure sensor mat/carpet will be expected in the future.
6. Conclusions
In this study, we examined three of mathematical models for the gait analysis. Table 1 shows the usefulness, possibility and the pre-requisite of each model. As a result, the authors concluded that our proposed abbreviated upper body model, Model C can be used with satisfied accuracy and convenience in the experimental configuration. Because, Model C requires additional one single reflective marker to the classical lower body model. This additional one marker would be the representative of the upper body. Also, whole bodied abbreviated model, Model C do not require force platform. That means a gait analysis on the stair or even the outside rough terrain can be achieved by this model. However, in this study, since we calculated the lower limb joint torques using the location of center of pressure obtained by the force platforms, we need a further investigation the equipment or method for measuring of the center of pressure for the improvement of joint torque estimation.

Table 1.
Usefulness, availability and pre-requisite of each model.
Supplementary Materials
The following supporting information can be downloaded at: www.mdpi.com/xxx/s1.
References
- Miyazaki, S.; Iwakura, H. A Device for Continuous Measurement of Vertical Foot Force during Walking. Jpn. J. Med. Electron. Biol. Eng. 1977, 15, 487–492. [Google Scholar]
- Oda, J.; Yasuda, A. Dynamic Analysis of Normal Walking by Foot Pressure Distributions. Trans. Jpn. Soc. Mech. Eng. Ser. A 1991, 57, 994–999. [Google Scholar] [CrossRef][Green Version]
- Sakurai, S.; Sakamoto, M.; Nakazawa, R.; Kawagoe, M.; Kato, K. Investigation of the Reproducibility of a 3D Accelerometer-Based Gait Analysis System of the Tibia. Soc. Phys. Ther. Sci. 2010, 25, 7–12. [Google Scholar] [CrossRef][Green Version]
- Zaizen, T.; Koseki, H.; Tanaka, R.; Kawasaki, T.; Koseki, T.; Tame, K.; Hirayama, T.; Koseki, T.; Kawama, K. Effects of Sole Grounding Timing and a Heel-arch Pad on Lower Limb Muscle Activities during Gait. Soc. Phys. Ther. Sci. 2013, 28, 45–48. [Google Scholar] [CrossRef][Green Version]
- Michiyoshi, A.E.; Tang, H.; Yokoi, T. Estimation of Inertia Properties of the Body Segments in Japanese Athletes. Soc. Biomech. Jpn. 1992, 11, 23–33. [Google Scholar]
- Okada, H.; Michiyoshi, A.E.; Fujii, N.; Morioka, Y. Body segment inertia properties of Japanese elderly. Soc. Biomech. 1996, 13, 125–139. [Google Scholar]
- Nishikawa, K.; Ohgi, Y.; Ohta, K. An estimation of the force acting on the lower limbs by the statics approximation method. Jpn. Soc. Clin. Biomech. 2014. [Google Scholar]
- Winter, D.A. Biomechanics and Motor Control of Human Movement, 2nd ed.; Wiley: Hoboken, NJ, USA, 1990. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).