Abstract
A mapping of non-extensive statistical mechanics with non-additivity parameter into Gibbs’ statistical mechanics exists (E. Vives, A. Planes, PRL 88 2, 020601 (2002)) which allows generalization to both of Einstein’s formula for fluctuations and of the ’general evolution criterion’ (P. Glansdorff, I. Prigogine, Physica 30 351 (1964)), an inequality involving the time derivatives of thermodynamical quantities. Unified thermodynamic description of relaxation to stable states with either Boltzmann () or power-law () distribution of probabilities of microstates follows. If a 1D (possibly nonlinear) Fokker-Planck equation describes relaxation, then generalized Einstein’s formula predicts whether the relaxed state exhibits a Boltzmann or a power law distribution function. If this Fokker-Planck equation is associated to the stochastic differential equation obtained in the continuous limit from a 1D, autonomous, discrete, noise-affected map, then we may ascertain if a a relaxed state follows a power-law statistics—and with which exponent—by looking at both map dynamics and noise level, without assumptions concerning the (additive or multiplicative) nature of the noise and without numerical computation of the orbits. Results agree with the simulations (J. R. Sánchez, R. Lopez-Ruiz, EPJ 143.1 (2007): 241–243) of relaxation leading to a Pareto-like distribution function.
Keywords:
non-extensive thermodynamics; non-equilibrium thermodynamics; probability distribution; power laws; nonlinear Fokker-Planck equation; discrete maps PACS:
05.70.Ln
1. The Problem
Usefulness of familiar, Gibbs’ thermodynamics lies in its ability to provide predictions concerning systems at thermodynamical equilibrium with the help of no detailed knowledge of the dynamics of the system. The distribution of probabilities of the microstates in canonical systems described by Gibbs’ thermodynamics is proportional to a Boltzmann exponential.
No similar generality exists for those systems in steady, stable (‘relaxed’) state which interact with external world, which are kept far from thermodynamical equilibrium by suitable boundary conditions and where the probability distribution follows a power law. (Here we limit ourselves to systems where only Boltzmann-like or power-law-like distributions are allowed). Correspondingly, there is no way to ascertain whether the probability distribution in a relaxed state is Boltzmann-like or power-law-like, but via solution of the detailed equations which rule the dynamics of the particular system of interest. In other words, if we dub ‘stable distribution function’ distribution of probabilities of the microstates in a relaxed state, then no criterion exists for assessing the stability of a given probability distribution—Boltzmann-like or power-law-like—against perturbations.
Admittedly, a theory exists—the so-called ‘non-extensive statistical mechanics’ [1,2,3,4,5,6]—which extends the formal machinery of Gibbs’ thermodynamics to systems where the probability distribution is power-law-like. Non-extensive statistical mechanics is unambiguously defined, once the value of a dimensionless parameter q is known; among other things, this value describes the slope of the probability distribution. If then the quantity corresponding to the familiar Gibbs’ entropy is not additive; Gibbs’ thermodynamics and Boltzmann’s distribution are retrieved in the limit . Thus, if we know the value of q then we know if the distribution function of a stable, steady state of a system which interacts with external world is Boltzmann or power law, and, in the latter case, what its slope is like. Unfortunately, the problem is only shifted: in spite of the formal exactness of non-extensive statistical mechanics, there is no general criterion for estimating q—with the exception, again, of the solution of the equations of the dynamics.
The aim of the present work is to find such criterion, for a wide class of physical sytems at least.
To this purpose, we recall that—in the framework of Gibbs’ thermodynamics—the assumption of ‘local thermodynamical equilibrium’ (LTE) is made in many systems far from thermodynamical equilibrium, i.e., it is assumed that thermodynamical quantities like pressure, temperature etc. are defined withn a small mass element of the system and that these quantities are connected to each other by the same rules—like e.g., Gibbs-Duhem equation—which hold at true thermodynamical equilibrium. If, furthermore, LTE holds at all times during the evolution of the small mass element, then the latter satisfies the so-called ‘general evolution criterion’ (GEC), an inequality involving total time derivatives of thermodynamical quantities [7]. Finally, if GEC holds for arbitrary small mass element of the system, then the evolution of the system as a whole is constrained; if such evolution leads a system to a final, relaxed state, then GEC puts a constraint on relaxation.
Straightforward generalization of these results to the non-extensive case is impossible. In this case, indeed, the very idea of LTE is scarcely useful: the entropy being a non-additive quantity, the entropy of the system is not the sum of the entropies of the small mass elements the system is made of, and no constraint on the relaxation of the system as a whole may be extracted from the thermodynamics of its small mass elements of the system. (For mathematical simplicity, we assume q to be uniform across the system).
All the same, an additive quantity exists which is monotonically increasing with the entropy (and achieves therefore a maximum if and only if the entropy is maximum) and which reduces to Gibbs’ entropy as . Thus, the case may be unambiguously mapped onto the corresponding Gibbs’ problem [8], and all the results above still apply. As a consequence, a common criterion of stability exists for relaxed states for both and . The class of perturbations which the relaxed states satisfying such criterion may be stable against include perturbations of q.
We review some relevant results of non-extensive thermodynamics in Section 2. The role of GEC and its consequences in Gibbs’ thermodynamics is discussed in Section 3. Section 4 discusses generalization of the results of Section 3 to the case. Section 5 shows application to a simple toy model. We apply the results of Section 5 to a class of physical problems in Section 6. Conclusions are drawn in Section 7. Entropies are normalized to Boltzmann’s constant .
2. Power-Law vs. Exponential Distributions of Probability
For any probability distribution defined on a set of microstates of a physical system, the following quantity [1]
is defined, where is the inverse function of and .
For an isolated (microcanonical) system, constrained maximization of leads to for all k’s and to , the constraint being given by the normalization condition .
For non-isolated systems [2,8], some () quantities—e.g., energy, number of particles etc.—whose values label the k-th microstate and which are additive constants of motion in an isolated system become fixed only on average (the additivity of a quantity signifies that, when the amount of matter is changed by a given factor, the quantity is changed by the same factor [9]). Maximization of with the normalization condition and the further M constraints const. (each with Lagrange multiplier and ; repeated indices are summed here and below) leads to , , and to the following, power-law-like probability distribution:
Remarkably, Equation (53) of [2] and Equation (6) of [3] show that suitable rescaling of the ’s allows us to get rid of the denominator in the ’s and to make all computations explicit—in the case at least. Finally, if we apply a quasi-static transformation to a state then:
If then Equations (1) and (2) lead to Gibbs’ entropy and to Boltzmann’s, exponential probability distribution respectively.
Many results of Gibbs’ thermodynamics still hold if . For example, a Helmholtz’ free energy still links and the usual way [2,4]. Moreover, if two physical systems and are independent (in the sense that the probabilities of + factorize into those of and of ) then we may still write for the averaged values of the additive quantities [2]
Generally speaking, however, Equation (4) does not apply to , which satisfies:
3.
Equations (4) and (5) are relevant when it comes to discuss stability of the system + against perturbations localized inside an arbitrary, small subsystem . (It makes still sense to investigate the interaction of and while dubbing them as ‘independent’, as far as the internal energies of and are large compared with their interaction energy [9]). Firstly, we recollect some results concerning the well-known case ; then, we investigate the problem.
To start with, we assume that ; generalization to follows. We are free to choose and to be the energy and the volume of the system in the k-th microstate respectively. Then and [4] with and where , , and are the familiar absolute temperature, pressure, internal energy and volume respectively. In the limit we have , , the familiar thermodynamical relationships and are retrieved, and Equation (3) is just a simple form of the first principle of thermodynamics.
Since , Equation (5) ensures additivity of Gibbs’ entropy. We assume to be is at thermodynamical equilibrium with itself, i.e., to maximize (LTE). We allow to be also at equilibrium with the rest of the system + , until some small, external perturbation occurs and destroys such equilibrium. The first principle of thermodynamics and the additivity of lead to Le Chatelier’s principle [9]. In turn, such principle leads to 2 inequalities, and . States in which such inequalities are not satisfied are unstable.
Let us introduce the volume , the mass density and the mass of . (Just like , here and in the following we refer to the value of the generic physical quantity a at the center of mass of as to ‘the value of a in ’; this makes sense, provided that is small enough). Together with the additivity of Gibbs’ entropy, arbitrariness in the choice of ensures that where and s are Gibbs’ entropy of the whole system and Gibbs’ entropy per unit mass respectively; here and in the following, integrals are extended to the whole system + . The internal energy per unit mass u and the volume per unit mass () may similarly be introduced, as well as the all the quantities per unit mass corresponding to all the ’s which satisfy Equation (4). Inequalities and lead to and respectively.
We relax the assumption . If contains particles of chemical species, each with particles with mass and chemical potential , then N degrees of freedom add to the 2 degrees of freedom U and V, i.e., . In the k-th microstate, is the number of particles of the h-th species. In analogy with U and V, we write . Starting from this M additive quantities, different M-ples of coordinates (thermodynamical potentials) may be selected with the help of Legendre transforms. LTE implies minimization of Gibbs’ free energy at constant T and p. As for quantities per unit mass, this minimization leads to the inequality [10] where , , . Identity reduces M by 1. With this proviso, we conclude that validity of LTE in A requires:
where means that all ’s are kept fixed, and ≥ is replaced by = only for . The 1st, 2nd and 3rd inequality in Equation (6) refer to thermal, mechanical and chemical equilibrium respectively.
Remarkably, Equation (6) contains information on only; has disappeared altogether. Thus, if we allow to change in time (because of some unknown, physical process occurring in , which we are not interested in at the moment) but we assume that LTE remains valid at all times within followed along its center-of-mass motion ( being the velocity of the center-of-mass), then Equation (6) remains valid in at all times. In this case, all relationships among total differentials of thermodynamic quantities—like e.g., Gibbs-Duhem equation—remain locally valid, provided that the total differential of the generic quantity a is where . Thus, Equation (6) leads to the so called ‘general evolution criterion’ (GEC) [7,11]
No matter how erratic the evolution of is, if LTE holds within at all times then the (by now) time-dependent quantities , etc. satisfy Equation (7) at all times.
GEC is relevant to stability. By ’stability’ we refer to the fact that, according to Einstein’s formula [9], deviations from the state which lead to a reduction of Gibbs’ entropy () have vanishing small probability . Such deviations can e.g., be understood as a consequence of an internal constraint which causes the deviation of the system from the equilibrium state, or as a consequence of contact with an external bath which allows changes in parameters which would be constant under total isolation. Let us characterize this deviation by a parameter which vanishes at equilibrium. Einstein’s formula implies that small fluctuations near the configuration which maximizes are Gaussian distributed with variance .
Correspondingly, as far as is at LTE deviations of the probability distribution from Boltzmann’s exponential distribution are also extremely unlikely. As evolves, the instantaneous values of the ’s and the ’s may change, but if LTE is to hold then the shape of remains unaffected. For example, T may change in time, but the probability of a microstate with energy E remains . Should Boltzmann’s distribution becomes unstable at any time—i.e., should any deviation of from Boltzmann’s distribution ever fail to fade out—then LTE too should be violated, and Equation (7) cease to hold. Then, we conclude that if remains Boltzmann-like in at all times then Equation (7) remains valid in at all times.
As for the evolution of the whole system + as a whole, if LTE holds everywhere throughout the whole system at all times then Equation (7) too holds everywhere at all times. In particular, let the whole system + evolve towards a final, relaxed state, where we maintain—as a working hypothesis—that the word ‘steady’ makes sense, possibly after time-averaging on some typical time scales of macroscopic physics. Since LTE holds everywhere at all times during relaxation, Equation (7) puts a constraint on relaxation everywhere at all times; as a consequence, it provides us with information about the relaxed state as well. In the following, we are going to show that some of the above result find its counterpart in the case.
4.
If then Equation (5) ensures that is not additive; moreover, it is not possible to find a meaningful expression for s such that , and the results of Section 3 fail to apply to (see Appendix A). All the same, even if the quantity
is additive and satisfies the conditions and
so that if and only if [1,4,8,12]. Then, a power-law-like distribution Equation (2) corresponds to . Moreover, the additivity of makes it reasonable to wonder whether a straightforward, step-by-step repetition of the arguments of Section 3 leads to their generalization to the case. When looking for an answer, we are going to discuss each step separately.
First of all, the choice of the ’s does not depend on the actual value of q; then, the ’s are unchanged, and Equation (4) still holds as it depends only on the averaging procedure on the ’s. As anticipated, Equation (2) corresponds to a maximum of , and we replace Equation (5) with
Since we are interested in probability distributions which maximize , hence , we are allowed to invoke Equations (11) and (12) of [8] and to write the following generalization of Equation (3):
Once again, we start with and choose and to be the energy and the volume of the system in the k-th microstate respectively. Together, Equations (11) and (12) and the identity give and , i.e., we retrieve the usual temperature and pressure of the case [12].
At last, Equations (4) and (10) allow us to repeat step-by-step the proof of Equation (6) and of Equation (7), provided that LTE now means that is in a state which corresponds to a maximum of . This way, we draw the conclusion that GEC takes exactly the same form Equation (7) even if . In detail, we have shown that both T, p, and (i.e., U and V) are unchanged; the same holds for u and . The 2nd inequality in Equation (6) remains unchanged: indeed, this is equivalent to say that the speed of sound remains well-defined in a system—see e.g., [13]. Admittedly, both the entropy per unit mass and the chemical potentials change when we replace with . However, has the same sign of because and ( ∝ a specific heat) is [5]. Thus, the 1st inequality in Equation (6) still holds because of the additivity of . Finally, maximization of Gibbs’ free energy at fixed T and p follows from maximization of as well as from Equations (4) and (10), and the 3rd inequality in Equation (6) remains valid even if the actual values of the ’s may be changed.
Even the notion of stability remains unaffected. Equation (18) of [8] generalizes Einstein’s formula to and ensures that strong deviations from the maximum of are exponentially unlikely. As a further consequence of generalized Einstein’s formula, if the deviation is characterized by a parameter which vanishes at equilibrium, then Equation (21) of [8] ensures that small fluctuations near the configuration which maximizes are Gaussian distributed with variance (and fluctuations may be larger than fluctuations).
In spite of Equation (5), Equation (9) allows us to extend some of our results to . We have seen that configurations maximizing maximize also (where is considered for the whole system + ). Analogously, Equation (9) implies . Given the link between and Equation (2), we may apply step-by-step our discussion of Botzmann’s distribution to power-law distributions. By now, the role of is clear: it acts as a dummy variable, whose additivity allows us to extend our discussion of Boltzmann’s distribution to power-law distributions in spite of the fact that is not additive.
Our discussion suggests that if relaxed states exist, then thermodynamics provides a common description of relaxation regardless of the actual value of q. As a consequence, thermodynamics may provide information about the relaxed states which are the final outcome of relaxation. Since relaxed states are stable against fluctuations and are endowed with probability distributions of the microstates, such information involves stability of these probability distributions against fluctuations. Since thermodynamics provides information regardless of q, such information involves Boltzmann exponential and power-law distributions on an equal footing. We are going to discuss such information in depth for a toy model in Section 5. In spite of its simplicity, the structure of its relaxed states are far from trivial.
Below, it turns to be useful to define the following quantities. In the case we introduce the contribution to of the irreversible processes occurring in the bulk of the whole system ( is often referred to as in the literature); by definition, such processes raise by an amount in a time interval . During relaxation, is a function of time t, and is constrained by Equation (7). A straightforward generalization of to is , where is the growth of due to irreversible processes in the bulk; is constrained by the version of Equation (7) in exactly the same way of the case. Finally, it is still possible to define such that the irreversible processes occurring in the bulk of the whole system raise by an amount . As usual by now, and . We provide an explicit epxression for in our toy model below.
5. A Toy Model
5.1. A Simple Case
The discussion of Section 4 does not rely on a particular choice of the ’s, as the latter may be changed via Legendre transforms and their choice obviously leaves the actual value of amount of heat produced in the bulk unaffected. Moreover, it holds regardless of the actual value of M as . As an example, we may think e.g., of a system with just one chemical species, the volume of the system in the k-th microstate is fixed and the energy of the k-th microstate may change because of exchange of heat with the external world. Finally, our discussion is not limited to three-dimensional systems. We focus on a toy model with just 1 degree of freedom, which we suppose to be a continuous variable (say, x) for simplicity so that we may replace with a distribution function satisfying the normalization condition at all times. We do not require that x retains its original meaning of energy: it may as well be the position of a particle. Here and below, integrals are performed on the whole system unless otherwise specified. The x runs within a fixed 1-D domain, which acts as a constant V. In our toy model, the impact of a driving force is contrasted by a diffusion process with constant and uniform diffusion coefficient . Following [14], we write the equation in in the form of a non linear Fokker Planck equation:
Here is a constant, effective friction coefficient, , and we drop the dependence on both x and t for simplicity here and in the following, unless otherwise specified.
The value of q is assumed to be both known and constant in Equation (13). Furthermore, if the value of q is known and a relaxed state exists, then Equation (13) describes relaxation. Now, if we allow q to change in time () much more slowly than the relaxation described by Equation (13), then the evolution of the system is a succession of relaxed states. Section 4. Unfortunately, available, GEC-based stability criteria [11] are useless, as they have been derived for perturbations at constant q only. In order to solve this conundrum, and given the fact that the evolution of the system is a succession of relaxed states, we start with some information about such states.
5.2. Relaxed States
In relaxed states and Equation (13) implies
where the value of J depends on the boundary conditions (e.g., the flow of P across the boundaries). In particular, the probability distribution [15]:
solves Equation (13) if and only if everywhere, i.e., if and only if the quantity
vanishes. The solution Equation (15) is retrieved in applications—see e.g., Equation (6) in [16] and Equation (2) of [17]. The proportionality constant in the R.H.S. of Equation (15) is fixed by the normalization condition . The quantity in Equation (16) is the amount of entropy [14]
produced per unit time in the bulk; even if Equations (10), (11), (42) and (44) of [14] give:
and in the R.H.S. of Equation (18) one identifies the entropy flux, representing the exchanges of entropy between the system and its neighborhood per unit time, in the words of [14]. In relaxed states such amount is precisely equal to because .
Admittedly, Equations (16) and (17) deal with , rather than with q. In contrast, it is q which appears in Equation (15). Replacing q with is equivalent to replace with ; however, the duality of non-extensive statistical mechanics—see Section 2 of [18] and Section 6 of [19]—ensures that no physics is lost this way ( replaces , etc.). Following Section III of [20], we limit ourselves to for ; the symmetry allow us therefore to focus further our attention on the interval [8]. Not surprisingly, if then and Equations (15) and (17) reduce to Boltzmann’s exponential (where corresponds to ) and to Gibbs’ entropy respectively.
At a first glance, is defined in two different ways, namely Equations (1) and (17). However, identities and allow Equations (1) and (17) to agree with each other, provided that we identify and ; according to Equation (15), this is equivalent to a rescaling of and x. Comparison of Equations (1) and (17) explains why it is not possible to find a meaningful expression for the entropy per unit mass s unless — see Appendix A.
According to [14], a H-theorem exists for Equation (13) even if , as far as , and A is ‘well-behaved at infinity’, i.e., ; relaxed states minimize a suitably defined Helmholtz’ free energy. ‘Equilibrium’ () occurs [2,15,20] when Equation (15) holds, i.e., for , and ; boundary conditions may keep the relaxed system ‘far from equilibrium’ (, , ).
If then Equations (16) and (18) ensure that no exchange of entropy between the system and its neighborhood occurs and that regardless of . The probability distribution in the relaxed state of isolated systems is a Boltzmann’s exponential. It is the the interaction with the external world (i.e., those boundary conditions which keep J far from 0) which allows the probability distribution in the relaxed state of non-isolated systems to differ from a Boltzmann’s exponential.
5.3. Weak Dissipation
The definition of J and Equation (16) show how depends on . We may write this dependence more explicitly in the weak dissipation limit. We show in Appendix B that:
where , and as . Together, Equations (19)–(22) allow computation of (hence, of ) once and D are known.
5.4. Stable Distributions of Probability
The evolution of the system is a succession of relaxed states, whose nature depends on J. If then Gibbs’ statistics holds and the probability distribution of the relaxed state is a Boltzmann exponential.
For weakly dissipating systems is small and each relaxed state is approximately an equilibrium (, hence ). It follows that Equation (15) describes the probability distribution and that small fluctuations near a relaxed state are Gaussian distributed with variance .
Now, stability requires that fluctuations, once triggered, relax back to the initial equilibrium state, sooner or later. In other words, the larger the variance the larger the fluctuations of which the relaxed state is stable against. Accordingly, the relaxed state which is stable against the fluctuations of of largest variance corresponds to . Then, Equation (9) gives .
Arbitrariness in the definition of allows us to identify it with a perturbation of z (so that ). Moreover, for small (i.e., negligible entropy flux across the boundary) Equation Equation (18) makes any increase of in a given time interval to be equal to , so that . Thus, the most stable probability distribution (i.e., the probability distribution which is stable against the fluctuations of z of largest amplitude) is given by Equation (15) with and such that:
According to Equation (23), achieves an extremum value at . In order to ascertain if this extremum is a maximum or a minimum, we recall that the change in due to a fluctuation of z around occurring in a time interval is (this is true for as fluctuations involve irreversible processes and for as Equation (7) describes relaxation the same way regardless of the value of z); it achieves its minimum value 0 if and the relaxed state is a true equilibrium (, ). In the weak dissipation limit the structure of the relaxed state is perturbed only slightly, and we may still reasonably assume even if its value is (again, Equation (7) acts the same way). In agreement with Equation (23), we obtain:
Remarkably, Equations (23) and (24) hold regardless of the actual relaxation time of the fluctuation; it applies therefore also to the slow dynamics of . We stress the point that Equations (23) and (24) have no means been said to ensure the actual existence of a relaxed configuration in the weak dissipation limit with something like a most stable probability distribution. But if such a thing exists, then it behaves as a power law with exponent if , where corresponds to a minimum of according to Equations (23) and (24). We rule out Boltzmann exponential in this case; indeed, if the power law is stable at all then it is stable against larger fluctuations than the Boltzmann exponential, because fluctuations are larger for than for [8]. Together, Equations (19)–(24) provide us with once and D are known. We discuss an application below.
6. The Impact of Noise on 1D Maps
6.1. Boltzmann vs. Power Law
We apply the results of Section 5 to the description of the impact of noise on maps. Let us introduce a discrete, autonomous, one-dimensional map
where , for all i’s, the initial condition is known and G is a known function of its argument. If the system evolves all along a time interval , then Equation (25) leads to the differential equation , provided that we define , identify and with and respectively, write and consider a time increment (’continuous limit’). We suppose to be integrable and well-behaved at infinity (see Section 5).
Map Equation (25) includes no noise. The latter may be either additive or multiplicative, and may affect at any ‘time’ i; for instance, it may perturb . In the continuous limit, we introduce a distribution function such that is the probability of finding the coordinate in the interval between x and at the time . We discuss the role of the constant below. In order to describe the impact of noise, we modify the differential equation above as follows:
where , , the noise satisfies and , and the brackets denote time average [14]. We leave the value of z unspecified.
According to the discussion of Equation (18) of [20], Equation (26) is associated with Equation (13) which rules . The choice of D in Equation (13) is equivalent to the choice of the noise level in Equation (26), and our assumption that D is constant and uniform in Section 5 means just that the noise level is the same throughout the system at all times. Well-behavedness of A at infinity allows H-theorem to apply to Equation (13). Let a relaxed state exist as an outcome of the evolution described by Equation (13). We know nothing about . For the moment, let us discuss the case .
If then the definition of J in Equation (13) allows us to choose a value large enough that the weak dissipation limit of small applies. Once the dynamics (i.e., the dependence of G on its own argument) and the noise level (i.e., D) are known, then Equations (19)–(22) allow us to compute the value of z which minimizes . According to our discussion of Equations (23) and (24) in Section 5, if such minimum exists and then the most stable probability distribution is power-like with exponent . Otherwise, no relaxed state may exist for . If, nevertheless, such state exists, then and its probability distribution is a Boltzmann exponential.
We have just written down a criterion to ascertain whether the outcome of a map Equation (25) follows an exponential or a power law distribution function as (and provided that such a distribution function may actually be defined in this limit) whenever the map is affected by noise, and regardless of the nature (additive or multipicative) of the latter. Only the map dynamics and the noise level D are required. In contrast with conventional treatment, no numerical solution of Equation (25) is required, and, above all, q is no ad hoc input anymore. This is the criterion looked for in Section 1.
6.2. An Example
As an example, we consider the map (25) where
and r and a are real, positive numbers. For typical values and Equations (25) and (27) are relevant in econophysics, where x and P are the wealth and the distribution of richness respectively. We refer to Ref. [21]—and in particular to its Equation (2)—where noise is built in to the initial conditions (which are completely random), and after a transient the system relaxes to a final, asymptotical state, left basically unaffected by fluctuations.
We assume everywhere in the following. Figure 1 displays (normalized to ) vs. z as computed from Equations (19)–(22) and (27) at various values of r and with the same value of . When dealing with Equation (19) we have taken into account powers of z up to (included). We performed all algebraic computations and definite integrals with the help of MATHCAD software. If then no is found which satisfies both Equations (23) and (24), so that Boltzmann distribution is expected to describe the asymptotic dynamical state of the system. This is far from surprising, as only damping counteracts noise in Equation (26) in the limit, like in a Brownian motion. In contrast, if then all ’s lies well inside the interval , and a power law is expected to hold; the correponding exponential depends on r only weakly—see Figure 2—as the values of the ’s are quite near to each other. Finally, Figure 3 displays how depends on D (i.e., the noise level) at fixed r; it turns out that noise tends to help relaxation to Boltzmann’s distribution, as expected.
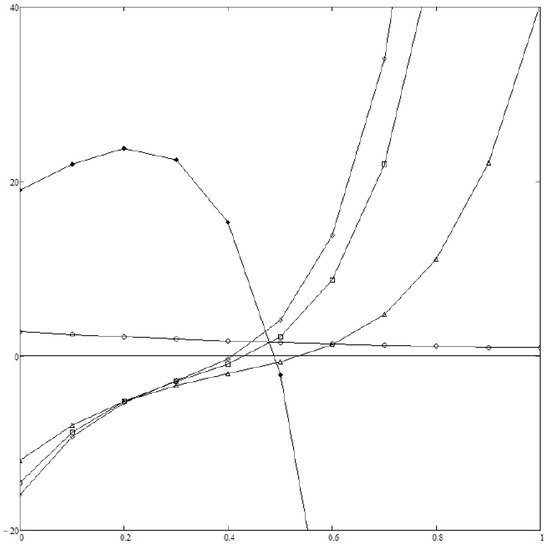
Figure 1.
(vertical axis) vs. z (horizontal axis) for (black diamonds), (empty circles), (triangles), (squares), (empty diamonds). In all cases . If then the slope of the curve at the point where it crosses the axis is negative, i.e., Equation (24) is violated. If then lies outside the interval , i.e., Equation (23) is violated. Both Equations (23) and (24) are satisfied for (with ), (with ) and (with ).
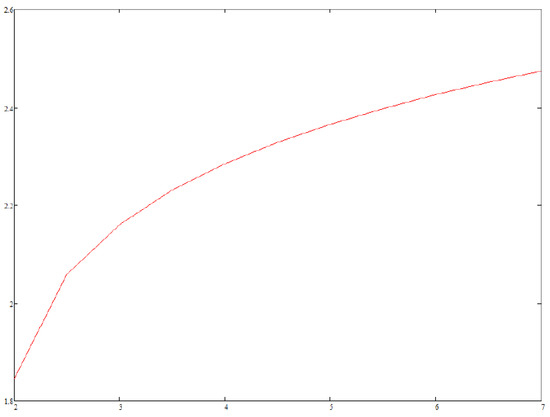
Figure 2.
Exponent (vertical axis) of the power-law distribution function of the relaxed state vs. r (horizontal axis).
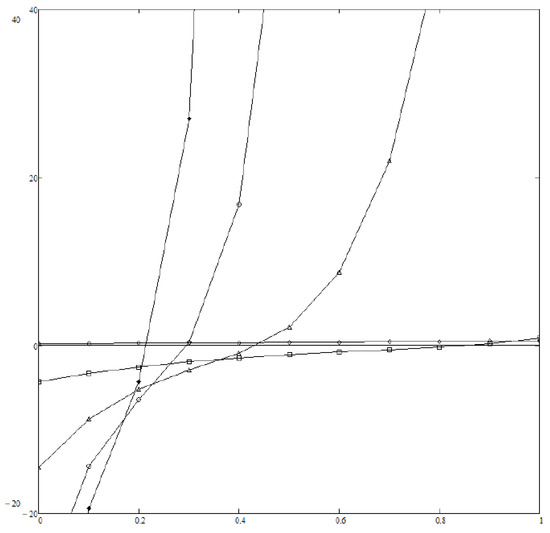
Figure 3.
(vertical axis) vs. z (horizontal axis) for (black diamonds), (empty circles), (triangles), (squares), (empty diamonds). In all cases . Even if a relaxed state exists, the larger D, the stronger the noise, the nearer to the bounds of the interval . If then does not belong to the interval, and Boltzmann’s exponential distribution rules the relaxed state.
Our results seem to agree with the results of the numerical simulations reported in [21]. If then the average value of x relaxes to zero (just as predicted by standard analysis of Equation (25) in the zero-noise case) and random fluctuations occur. In contrast, if then the typical amplitude of the fluctuations is much larger; nevertheless, a distribution function is clearly observed, which exhibits a distinct power-law, Pareto-like behaviour. The exponent is 2.21, in good agreement with the values displayed in our Figure 2. (The exponent in Pareto’s law is ≈2.15). We stress the point that we have obtained our results with no numerical solution of Equation (25) and with no postulate concerning non-extensive thermodynamics, i.e., no assumption on q.
7. Conclusions
Gibbs’ statistical mechanics describes the distribution of probabilities of the microstates of (grand-)canonical systems at thermodynamical equilibrium with the help of Boltzmann’s exponential. In contrast, this distribution follows a power law in stable, steady (‘relaxed’) states of many physical systems. With respect to a power-law-like distribution, non-extensive statistical mechanics [1,2] formally plays the same role played by Gibbs’ statistical mechanics with respect to Boltzmann distribution: a relaxed state corresponds to a constrained maximum of Gibbs’ entropy and to its generalization in Gibbs’ and non-extensive statistical mechanics respectively. Generalization of some results of Gibbs’ statistical mechanics to non-extensive statistical mechanics is available; the latter depends on the dimensionless quantity q and reduces to Gibbs’ statistical mechanics in the limit , just like reduces to Gibbs’ entropy in the same limit. The quantity q measures the lack of additivity of and provides us with the slope of the power-law-like distribution, the Boltzmann distribution corresponding to : is an additive quantity if and only if .
The overwhelming success of Gibbs’ statistical mechanics lies in its ability to provide predictions (like e.g., the positivity of the specific heat at constant volume) even when few or no information on the detailed dynamics of the system is available. Stability provides us with an example of such predictions. According to Einstein’s formula, deviations from thermodynamic equilibrium which lead to a significant reduction of Gibbs’ entropy () have vanishing small probability . In other words, significant deviations of the probability distribution from the Boltzmann exponential are exponentially unlikely in Gibbs’ statistical mechanics.
Moreover, additivity of and of other quantities like the internal energy allows to write all of them as the sum of the contributions of all the small parts the system is made of. If, furthermore, every small part of a physical system corresponds locally to a maximum of (‘local thermodynamical equilibrium, LTE) at all times during the evolution of the system, then this evolution is bound to satisfy the so-called ‘general evolution criterion’ (GEC) [7], an inequality involving total time derivatives of thermodynamical quantities which follows from Gibbs-Duhem equation. In particular, GEC applies to the relaxation of perturbations of a relaxed state of the system, if any such state exists.
In contrast, lack of a priori knowledge of q limits the usefulness of non-extensive statistical mechanics; for each problem, such knowledge requires either solving the detailed equations of the dynamics (e.g., the relevant kinetic equation ruling the distribution probability of the system of interest) or performing a posteriori analysis of experimental data, thus reducing the attractiveness of non-extensive statistical mechanics.
However, it is possible to map non-extensive statistical mechanics into Gibbs’ statistical mechanics [1,4,8]. A quantity exists which is both additive and monotonically increasing function of for arbitrary q. Thus, relaxed states of non-extensive thermodynamics correspond to , and additivity of allow suitable generalization of both Einstein’s formula and Gibbs-Duhem equation to [8], which in turn ensure that strong deviations from this maximum are exponentially unlikely and that LTE and GEC still hold, formally unaffected, in the case respectively.
These generalizations allow thermodynamics to provide an unified framework for the description of both the relaxed states (via Einstein’s formula) and the relaxation processes leading to them (via GEC) regardless of the value of q, i.e., of the nature—power law () vs. Boltzmann exponential ()—of the probability distribution of the microstates in the relaxed state.
For further discussion we have focussed our attention on the case of a continuous, one-dimensional system described by a nonlinear Fokker Planck equation [14], where the impact of a driving force is counteracted by diffusion (with diffusion coefficient D). It turns out that it is the the interaction with the external world which allows the probability distribution in the relaxed states to differ from a Boltzmann’s exponential. Moreover, Einstein’s formula in its generalized version implies that the value of of the ‘most stable probability distribution’ (i.e., the probability distribution of the relaxed state which is stable against fluctuations of largest amplitude) corresponds to a minimum of , being the amount of produced in a time interval by irreversible processes occurring in the bulk of the system. Finally, if a relaxed state exists and , then the most stable probability distribution is a power law with exponent ; otherwise, it is a Boltzmann exponential. Since depends just on z, D and the driving force, the value of —i.e., the selection of the probability distribution—depends on the physics of system only (i.e., on the diffusion coefficient and the driving force): a priori knowledge of q is required no more.
We apply our result to the Fokker Planck equation associated to the stochastic differential equation obtained in the continuous limit from a one-dimensional, autonomous, discrete map affected by noise. Since no assumption is made on q, the noise may be either additive or multiplicative, and the Fokker Planck equation may be either linear or nonlinear. If the system evolves towards a system which is stable against fluctuations then we may ascertain if a power-law statistics describes such state—and with which exponent—once the dynamics of the map and the noise level are known, without actually computing many forward orbits of the map.
As an example, we have analyzed the problem discussed in [21], where a particular one-dimensional discrete map affected by noise leads to an asymptotic state described by a Pareto-like law for selected values of a control parameter. Our results agree with those of [21] as far as both the exponent of the power law and the range of the control parameter, with the help of numerical simulation of the dynamics and of no assumption about q.
Extension to multidimensional maps will be the task of future work.
Acknowledgments
Useful discussions and warm encouragement with W. Pecorella, Università di Tor Vergata, Roma, Italy are gratefully acknowledged.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GEC | General evolution criterion |
| LTE | Local thermodynamical equilibrium |
Appendix A. Non-Existence of s for q ≠ 1
If then , which leads immediately to with and . Let us suppose that a similar expression holds for and . Of course, does not depend on q, so we keep even if . In the latter case, Equation (17) gives , and agreement of Equation (1) with Equation (17) requires that we identify and . However, this identification is possible at no value of , because the normalization conditions and make the ’s and P to transform like and respectively under the scaling transformation , so that and . Identification of and is impossible because these two quantities behave differently under the same scaling transformation; then, no definition of s is self-consistent unless .
This result follows from the non-additivity of : if then the entropy of the whole system is not the sum of the entropies of the small masses the systems is made of. Physically, this suggests that strong correlations exixt among such masses; indeed, strongly correlated variables are precisely the topic which non-extensive statistical mechanics is focussed on [6].
Accordingly, straightforward generalization of LTE and GEC with the help of to the case is impossible. This is why we need the additive quantity in order to build a local thermodynamics, and to generalize the results of Section 3 in Section 4. As discussed in the text, the results of Section 4 may involve rather than just because .
Appendix B. Proof of Equations (19)–(22)
We derive from both Equations (14) and (16) and the definition of J the Taylor-series development Equation (19) of in powers of z, centered in :
where and is the solution for arbitrary J with the boundary condition of Equation (13). Starting from Equations (13) and (15) (for ), the method of variation of constants gives:
The normalization condition holds
where is approximately given by Equation (15) in weakly dissipating systems. We assume and with no loss of generality (originally, is an energy). We define such that . It is unlikely that ; thus, we approximate Equation (A2) as:
According to Equation (A4), the domain of integration in Equation (19), Equations (A2) and (A3) reduces to . Thus, Equations (19) and (A4) lead to Equation (20), and Equations (A3) and (A4) lead to Equation (21). Finally, Equations (14), (18) and (A4) lead to: in relaxed state, while Equations (14), (16) and (A4) give: . After eliminating and replacing the definition of we obtain Equation (22).
References
- Tsallis, C.J. Possible Generalization of Boltzmann-Gibbs Statistics. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C.; Mendes, R.S.; Plastino, A. The role of constraints within generalized nonextensive statistics. Phys. A 1998, 261, 534–554. [Google Scholar] [CrossRef]
- Tsallis, C.; Anteneodo, C.; Borland, L.; Osorio, R. Nonextensive statistical mechanics and economics. Phys. A Stat. Mech. Appl. 2003, 324, 89–100. [Google Scholar] [CrossRef]
- Abe, S. Heat and entropy in nonextensive thermodynamics: Transmutation from Tsallis theory to Rényi-entropy-based theory. Phys. A 2001, 300, 417–423. [Google Scholar] [CrossRef]
- Tatsuaki, W. On the thermodynamic stability conditions of Tsallis’ entropy. Phys. Lett. A 2002, 297, 334–337. [Google Scholar]
- Umarov, S.; Tsallis, C.; Steinberg, S. On a q-central limit theorem consistent with nonextensive statistical mechanics. Milan J. Math. 2008, 76, 307–328. [Google Scholar] [CrossRef]
- Glansdorff, P.; Prigogine, I. On a general evolution criterion in macroscopic physics. Physica 1964, 30, 351–374. [Google Scholar] [CrossRef]
- Vives, E.; Planes, A. Black Hole Production by Cosmic Rays. PRL 2002, 88, 021303. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics; Pergamon: Oxford, UK, 1959. [Google Scholar]
- Prigogine, I.; Defay, R. Chemical Thermodynamics; Longmans-Green: London, UK, 1954. [Google Scholar]
- Di Vita, A. Maximum or minimum entropy production? How to select a necessary criterion of stability for a dissipative fluid or plasma. Phys. Rev. E 2010, 81, 041137. [Google Scholar] [CrossRef] [PubMed]
- Marino, M. A generalized thermodynamics for power-law statistics. Phys. A Stat. Mech. Its Appl. 2007, 386, 135–154. [Google Scholar] [CrossRef]
- Khuntia, A.; Sahoo, P.; Garg, P.; Sahoo, R.; Cleymans, J. Speed of Sound in a System Approaching Thermodynamic Equilibrium; DAE Symp. Nucl. Phys. 2016, 61, 842–843. [Google Scholar]
- Casas, G.A.; Nobre, F.D.; Curado, E.M.F. Entropy production and nonlinear Fokker-Planck equations. Phys. Rev. E 2012, 86, 061136. [Google Scholar] [CrossRef] [PubMed]
- Wedemann, R.S.; Plastino, A.R.; Tsallis, C. Nonlinear Compton scattering in a strong rotating electric field. Phys. Rev. E 2016, 94, 062105. [Google Scholar] [CrossRef] [PubMed]
- Haubold, H.J.; Mathai, A.M.; Saxena, R.K. Boltzmann-Gibbs Entropy Versus Tsallis Entropy: Recent Contributions to Resolving the Argument of Einstein Concerning “Neither Herr Boltzmann nor Herr Planck has Given a Definition of W”? Astrophys. Space Sci. 2004, 290, 241–245. [Google Scholar] [CrossRef]
- Ribeiro, M.S.; Nobre, F.D.; Curado, E.M.F. Time evolution of interacting vortices under overdamped motion. Phys. Rev. E 2012, 85, 021146. [Google Scholar] [CrossRef] [PubMed]
- Wada, T.; Scarfone, A.M. Connections between Tsallis’ formalisms employing the standard linear average energy and ones employing the normalized q-average energy. Phys. Lett. A 2005, 335, 351–362. [Google Scholar] [CrossRef]
- Naudts, J. Generalized thermostatistics based on deformed exponential and logarithmic functions. Phys. A Stat. Mech. Appl. 2004, 340, 32–40. [Google Scholar] [CrossRef]
- Borland, L. Microscopic dynamics of the nonlinear Fokker-Planck equation: A phenomenological model. Phys. Rev E 1998, 57, 6634. [Google Scholar] [CrossRef]
- Sánchez, J.R.; Lopez-Ruiz, R. A model of coupled maps for economic dynamics. Eur. Phys. J. Spec. Top. 2007, 143, 241–243. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).