An Evaluation of Heat Transfer Enhancement Technique in Flow Boiling Conditions Based on Entropy Generation Analysis: Micro-Fin Tube †
Abstract
:1. Introduction
2. Mathematical Modeling
3. Results and Discussions
3.1. The Geometrical Parameters of the Micro-Fin Tube
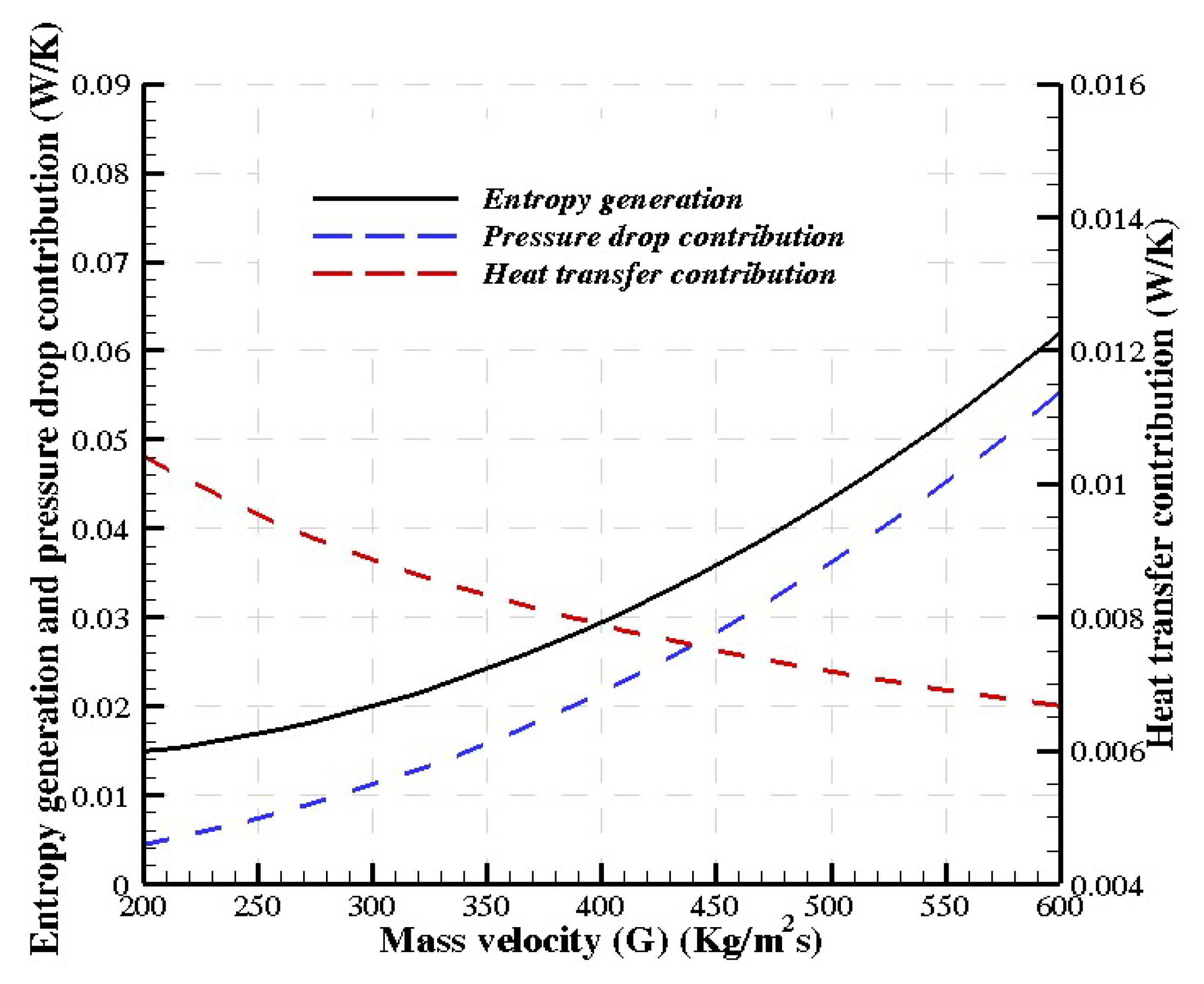
3.2. Change in Flow Conditions
4. Conclusions
Conflicts of Interest
Abbreviations
| A | Cross section (m2) |
| Cross sectional flow area (m2) | |
| Cross sectional tube wall area per fin (m2) | |
| Be | Bejan number (−) |
| Bottom thickness (m) | |
| Bottom width (m) | |
| Element discretization (m) | |
| Hydraulic diameter (m) | |
| Tube outer diameter (m) | |
| Fin height (m) | |
| G | Mass velocity () |
| H | Specific enthalpy () |
| L | Length (m) |
| Mass flow rate () | |
| N | Number of fins(−) |
| Entropy generation number (−) | |
| P | Pressure (Pa) |
| P | Perimeter (m) |
| Q | Heat flux () |
| Heat rate (W) | |
| S | Specific entropy () |
| Entropy generation per unit length () | |
| T | Temperature (˚C) |
| U | Convective heat transfer coefficient () |
| Liquid superfacial velocity () | |
| Gas superfacial velocity () | |
| Greek symbols | |
| Void fraction (−) | |
| Fin angle (deg.) | |
| Density () | |
| Fin spiral angle (deg.) | |
| Specific volume (m3) | |
| Subscripts | |
| ht | Heat transfer |
| in | Inlet |
| l | Liquid |
| pd | Pressure drop |
| sat | Saturation |
| tp | Two-phase |
| v | Vapor |
| w | Wall |
| x | Vapor quality |
References
- Abdous, M.A.; Saffari, H.; Avval, H.B.; Khoshzat, M. Investigation of entropy generation in a helically coiled tube in flow boiling condition under a constant heat flux. Int. J. Refrig. 2015, 60, 217–233. [Google Scholar] [CrossRef]
- Kaushik, S.C.; Manjunath, K. Second law analysis of condenser by using new heat transfer and pressure drop model based on flow regimes. Int. J. Exergy 2011, 9, 255–279. [Google Scholar] [CrossRef]
- Manjunath, K.; Kaushik, S.C. Second law thermodynamic study of heat exchangers: A review. Renew. Sustain. Energy Rev. 2014, 40, 348–374. [Google Scholar] [CrossRef]
- Manjunath, K.; Kaushik, S.C. Second law efficiency analysis of heat exchangers. Heat Transf. Res. 2015, 44, 89–108. [Google Scholar] [CrossRef]
- Naphon, P. Study on the exergy loss of the horizontal concentric micro-fin tube heat exchanger. Int. Commun. Heat Mass Transf. 2011, 38, 229–235. [Google Scholar] [CrossRef]
- Revellin, R.; Lips, S.; Khandekar, S.; Bonjour, J. Local entropy generation for saturated two-phase flow. Energy 2009, 34, 1113–1121. [Google Scholar] [CrossRef]
- Sciacovelli, A.; Verda, V.; Sciubba, E. Entropy generation analysis as a design tool—A review. Renew. Sustain. Energy Rev. 2015, 43, 1167–1181. [Google Scholar] [CrossRef]
- Türkakar, G.; Okutucu-Özyurt, T. Entropy generation analysis and dimensional optimization of an evaporator for use in a microscale refrigeration cycle. Int. J. Refrig. 2015, 56, 140–153. [Google Scholar] [CrossRef]
- Woldesemayat, M.A.; Ghajar, A.J. Comparison of void fraction correlations for different flow patterns in horizontal and upward inclined pipes. Int. J. Multiph. Flow 2007, 33, 347–370. [Google Scholar] [CrossRef]
- Wongsa-ngam, J.; Nualboonrueng, T.; Wongwises, S. Performance of smooth and micro-fin tubes in high mass flux region of R-134a during evaporation. Heat Mass Transf. 2002, 40, 425–435. [Google Scholar] [CrossRef]
- Ye, H.-Y.; Lee, K.-S. Refrigerant circuitry design of fin-and-tube condenser based on entropy generation minimization. Int. J. Refrig. 2012, 35, 1430–1438. [Google Scholar] [CrossRef]

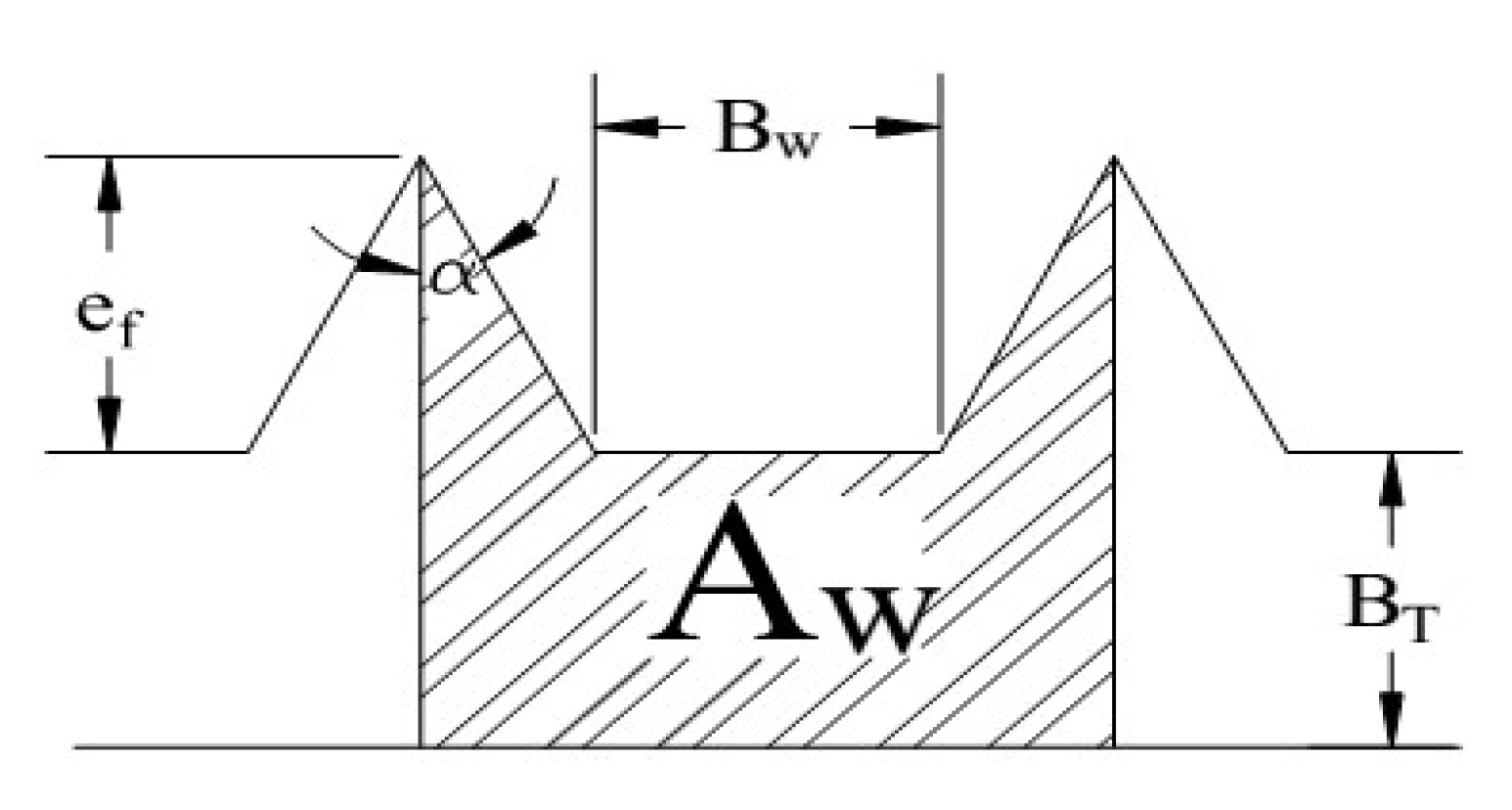


| 400 | 10 | 15 | 0.2 |
| (m) | ||||
|---|---|---|---|---|
| 0.2 | 0.27 | 60 | 0.3 | 2.5 |
| (m) | |||||
|---|---|---|---|---|---|
| 9.52 | 0.2 | 0.27 | 60 | 0.3 | 2.5 |
| 10 | 15 | 0.2 |
| 10 | 15 | 450 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdous, M.A. An Evaluation of Heat Transfer Enhancement Technique in Flow Boiling Conditions Based on Entropy Generation Analysis: Micro-Fin Tube. Proceedings 2018, 2, 149. https://doi.org/10.3390/ecea-4-05002
Abdous MA. An Evaluation of Heat Transfer Enhancement Technique in Flow Boiling Conditions Based on Entropy Generation Analysis: Micro-Fin Tube. Proceedings. 2018; 2(4):149. https://doi.org/10.3390/ecea-4-05002
Chicago/Turabian StyleAbdous, Mohammad Ali. 2018. "An Evaluation of Heat Transfer Enhancement Technique in Flow Boiling Conditions Based on Entropy Generation Analysis: Micro-Fin Tube" Proceedings 2, no. 4: 149. https://doi.org/10.3390/ecea-4-05002
APA StyleAbdous, M. A. (2018). An Evaluation of Heat Transfer Enhancement Technique in Flow Boiling Conditions Based on Entropy Generation Analysis: Micro-Fin Tube. Proceedings, 2(4), 149. https://doi.org/10.3390/ecea-4-05002




